基于自適應(yīng)強(qiáng)跟蹤C(jī)QKF的目標(biāo)跟蹤算法

劉暢， 楊鎖昌,*， 汪連棟， 張寬橋

(1. 軍械工程學(xué)院 導(dǎo)彈工程系, 石家莊 050000； 2. 電子信息系統(tǒng)復(fù)雜電磁環(huán)境效應(yīng)國(guó)家重點(diǎn)實(shí)驗(yàn)室, 洛陽 471003)

目標(biāo)跟蹤是一類典型的非線性濾波問題，貝葉斯估計(jì)理論為非線性濾波提供了嚴(yán)謹(jǐn)?shù)慕鉀Q框架。對(duì)于線性高斯系統(tǒng)，貝葉斯估計(jì)的最優(yōu)解為卡爾曼濾波[1]。但對(duì)于非線性高斯系統(tǒng)，很難得到高斯加權(quán)積分的解析解，因此科研人員提出了許多次優(yōu)非線性濾波方法。其中，擴(kuò)展卡爾曼濾波(Extented Kalman Filter,EKF)[2]由于簡(jiǎn)單高效得到廣泛應(yīng)用,但EKF采用非線性函數(shù)的一階泰勒展開近似非線性函數(shù)，對(duì)于強(qiáng)非線性系統(tǒng)會(huì)產(chǎn)生較大的近似誤差，且其需要計(jì)算雅可比矩陣，這既增加了計(jì)算復(fù)雜度也要求非線性函數(shù)連續(xù)可微。

為了克服EKF的缺點(diǎn)，隨機(jī)采樣型濾波器和確定采樣型濾波器分別被提出，其核心是用一組隨機(jī)或確定加權(quán)采樣點(diǎn)逼近狀態(tài)的后驗(yàn)分布，以采樣點(diǎn)的加權(quán)和近似“非線性函數(shù)×高斯函數(shù)”的積分。隨機(jī)采樣型濾波器的主要應(yīng)用形式——粒子濾波(Particle Filter,PF)[3]，以蒙特卡羅隨機(jī)采樣得到的粒子近似狀態(tài)后驗(yàn)分布，理論上適用于解決任意非線性濾波問題，但存在權(quán)值退化、粒子多樣性匱乏、實(shí)時(shí)性差等嚴(yán)重缺陷。依據(jù)采樣點(diǎn)選取策略的不同，確定采樣型濾波器主要分為中心差分卡爾曼濾波(Central Difference Kalman Filter,CDKF)[4]、無跡卡爾曼濾波(Unscented Kal-man Filter,UKF)[5]和容積卡爾曼濾波(Cubature Kalman Filter,CKF)[6]等。CDKF以多項(xiàng)式插值擬合逼近狀態(tài)后驗(yàn)分布，計(jì)算簡(jiǎn)單但濾波精度較低且易受參數(shù)取值影響。UKF以UT(Unsented Transformation)變換逼近狀態(tài)后驗(yàn)分布，能夠以二階泰勒精度逼近非線性狀態(tài)而計(jì)算量與EKF同階，但系統(tǒng)狀態(tài)維數(shù)大于3時(shí)，中心采樣點(diǎn)權(quán)值為負(fù)，從而引起協(xié)方差矩陣的非正定和濾波發(fā)散。CKF以三階球面-徑向容積準(zhǔn)則逼近狀態(tài)后驗(yàn)分布，其采樣點(diǎn)權(quán)值始終為正，且有嚴(yán)格的數(shù)學(xué)證明，與UKF相比濾波精度更高而計(jì)算量相近，因此，近年來得到了廣泛的應(yīng)用。

為進(jìn)一步提高CKF的精度，容積積分卡爾曼濾波(Cubature Quadrature Kalman Filter,CQKF)[7]以容積準(zhǔn)則和高斯-拉蓋爾積分準(zhǔn)則近似高斯加權(quán)積分，濾波精度與切比雪夫-拉蓋爾多項(xiàng)式的階數(shù)m成正相關(guān)關(guān)系。CQKF是CKF的拓展形式，當(dāng)m≥2時(shí)，其精度高于CKF。但CQKF要求系統(tǒng)模型和噪聲精確已知，而現(xiàn)代戰(zhàn)場(chǎng)復(fù)雜對(duì)抗環(huán)境使得系統(tǒng)模型具有很大的不確定性，系統(tǒng)狀態(tài)突變，過程噪聲及量測(cè)噪聲未知時(shí)變，從而造成CQKF濾波精度下降甚至發(fā)散。為解決噪聲統(tǒng)計(jì)特性未知情況下的濾波問題，貝葉斯法[8]、相關(guān)法[9-11]、協(xié)方差匹配法[12]和極大似然估計(jì)法[13]等多種噪聲估計(jì)算法分別被提出。貝葉斯法涉及到多重積分，計(jì)算量大且未必能得到最優(yōu)封閉解，多限于理論研究。相關(guān)法主要應(yīng)用于線性系統(tǒng)，其在非線性系統(tǒng)中的拓展尚未無偏性證明[14]。協(xié)方差匹配法是一種有偏估計(jì)方法，存在穩(wěn)態(tài)估計(jì)誤差且估計(jì)精度相對(duì)較低。極大似然估計(jì)法由于能夠直接構(gòu)造含有待估計(jì)參數(shù)的概率密度函數(shù)，且計(jì)算量適中而得到廣泛關(guān)注，其中以基于極大后驗(yàn)估計(jì)(Maximum A Posterior, MAP)準(zhǔn)則提出的Sage-Husa時(shí)變?cè)肼暯y(tǒng)計(jì)估值器[15]應(yīng)用最為廣泛。

基于上述考慮，本文提出了一種自適應(yīng)強(qiáng)跟蹤C(jī)QKF(AST-CQKF) 算法。AST-CQKF借鑒強(qiáng)跟蹤濾波(Strong Tracking Filter, STF)的思想，引入時(shí)變漸消因子對(duì)預(yù)測(cè)協(xié)方差矩陣在線調(diào)整，同時(shí)利用Sage-Husa時(shí)變?cè)肼暯y(tǒng)計(jì)估值器對(duì)噪聲統(tǒng)計(jì)特性實(shí)時(shí)估計(jì)，并將估計(jì)結(jié)果引入濾波迭代過程中，從而增加了CQKF算法的魯棒性和自適應(yīng)性。通過仿真實(shí)驗(yàn)驗(yàn)證了本文算法的有效性和可行性。

1 容積積分卡爾曼濾波

1.1 貝葉斯濾波框架

考慮如下非線性系統(tǒng)：

(1)

式中：xk∈Rn為k時(shí)刻的狀態(tài)向量；zk∈Rp為k時(shí)刻的量測(cè)向量；f:Rn→Rn和h:Rn→Rp為已知非線性函數(shù)；vk-1∈Rn和ηk∈Rp為不相關(guān)的高斯白噪聲，且vk-1～N(0,Qk-1)，ηk～N(0,Rk);Qk-1和Rk為噪聲協(xié)方差矩陣。

假設(shè)k-1時(shí)刻的后驗(yàn)概率密度函數(shù)為高斯分布，即

(2)

(3)

其中狀態(tài)一步預(yù)測(cè)及協(xié)方差為

(4)

(5)

輸出預(yù)測(cè)、自協(xié)方差及互協(xié)方差分別為

(6)

(7)

(8)

非線性系統(tǒng)式(1)在最小方差估計(jì)準(zhǔn)則下的最優(yōu)高斯濾波器為[16]

(9)

式中：

(10)

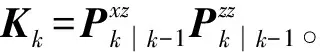
因此，貝葉斯濾波的核心問題轉(zhuǎn)化為計(jì)算形式如式(11)的積分表達(dá)式：

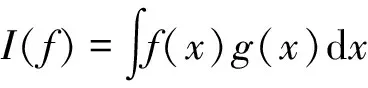
(11)

式中：f(x)為任意非線性函數(shù);g(x)為高斯密度函數(shù)。通常式(11)難以得到解析表達(dá)式，主要采取一系列采樣點(diǎn)ξj及其權(quán)值wj的加權(quán)和進(jìn)行數(shù)值近似，即

(12)

1.2 容積積分準(zhǔn)則

對(duì)于任意函數(shù)f(x)，X∈Rn，式(11)的一般形式為

(13)

可以在球面坐標(biāo)系中表示為[7]

μ)ds(Z)]rn-1e-r2/2dr

(14)

式中：X=CrZ+μ，且X～N(μ,Σ)，μ為高斯分布的均值，C為協(xié)方差矩陣Σ的Cholesky分解，即Σ=CCT；r和Z為積分變量；Un={Z∈RnZZT=1}為單位超球面；ds(·)為Un上的面積元素。

若μ=0且Σ為單位矩陣，則式(14)中的積分為

(15)

由三階球面-徑向容積準(zhǔn)則可以近似為

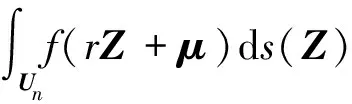
(16)

式中：Γ(·)為伽馬函數(shù)；[ui](i=1,2,…,2n)為位于單位超球面與坐標(biāo)軸交點(diǎn)的容積點(diǎn)，即完全對(duì)稱點(diǎn)集[1]的第i個(gè)列向量

[1]=

(17)

將式(16)代入式(14)，令λ=r2/2，則

λ(n/2-1)e-λdλ

(18)

根據(jù)高斯-拉蓋爾積分準(zhǔn)則，積分可以近似為

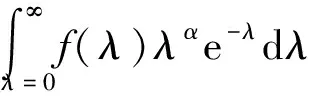
(19)

式中：積分點(diǎn)λj(j=1,2,…,m)為m階切比雪夫-拉蓋爾多項(xiàng)式的m個(gè)根，即λj滿足

(m+α)(m+α-1)λm-2-…=0

(20)

式中：α=n/2-1。

對(duì)應(yīng)的權(quán)值A(chǔ)j為

(21)

將式(19)～式(21)代入式(18)，則得到容積積分準(zhǔn)則為

(22)

由式(22)可知，對(duì)于如式(1)所示的n維狀態(tài)估計(jì)問題，需要計(jì)算滿足

(23)

的2mn個(gè)采樣點(diǎn)ξl(本文稱其為CQ點(diǎn))及對(duì)應(yīng)權(quán)值wl，其計(jì)算方式如下：

i=1,2,…,2n；j=1,2,…,m；l=1,2,…,2mn

(24)

(25)

1.3 CQKF算法

步驟1初始化。

1) 令

2) 根據(jù)式(24)和式(25)計(jì)算CQ點(diǎn)ξl及對(duì)應(yīng)權(quán)值wl。

步驟2預(yù)測(cè)更新。

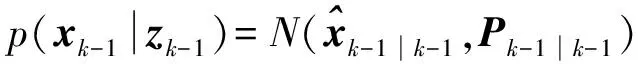
2) 計(jì)算CQ點(diǎn)：

3) 更新CQ點(diǎn)隨狀態(tài)方程的轉(zhuǎn)移：

4) 計(jì)算一步狀態(tài)預(yù)測(cè)及預(yù)測(cè)誤差協(xié)方差矩陣：

步驟3量測(cè)更新。

1) 分解協(xié)方差矩陣:

2) 計(jì)算CQ點(diǎn):

3) 更新CQ點(diǎn)隨量測(cè)方程的轉(zhuǎn)移:

Zl,kk-1=h(χl,kk-1)

4) 計(jì)算量測(cè)預(yù)測(cè)值：

5) 計(jì)算自協(xié)方差矩陣及互協(xié)方差矩陣：

6) 計(jì)算卡爾曼增益：

7) 估計(jì)狀態(tài)：

8) 估計(jì)狀態(tài)預(yù)測(cè)誤差協(xié)方差矩陣：

2 強(qiáng)跟蹤濾波理論

為了提高EKF對(duì)于系統(tǒng)模型不確定性及狀態(tài)突變的魯棒性，周東華等[17]提出的STF利用衰減記憶濾波思想，在計(jì)算預(yù)測(cè)誤差協(xié)方差矩陣時(shí)引入漸消因子，強(qiáng)迫殘差序列正交，從而保證濾波器對(duì)系統(tǒng)實(shí)際狀態(tài)的跟蹤效果。

非線性系統(tǒng)式(1)的STF方程為[18]

(26)

式中：

In×n為n階單位矩陣；λk為漸消因子，其計(jì)算式為

(27)

式中：

(28)

(29)

(30)

(31)

其中：tr(·)為矩陣求跡運(yùn)算；β≥1為弱化因子；0<ρ≤1為遺忘因子,通常取ρ=0.95。由于STF是EKF的改進(jìn)形式，在計(jì)算漸消因子時(shí)仍需要求解雅可比矩陣，因此不能直接將其引入CQKF，需要研究不利用Hk計(jì)算漸消因子的等價(jià)表述方式。文獻(xiàn)[19]給出了Hk、Nk和Mk的等效表述形式，即

(32)

(33)

(34)

(35)

漸消因子的具體引入方式見第4節(jié)。

3 時(shí)變?cè)肼暯y(tǒng)計(jì)估值器

考慮噪聲的一般形式，即vk-1∈Rn和ηk∈Rp是帶時(shí)變均值和協(xié)方差且線性無關(guān)的高斯白噪聲，且vk-1～N(qk-1,Qk-1)，ηk～N(rk,Rk)。針對(duì)qk、Qk、rk和Rk等噪聲參數(shù)的估計(jì)問題，文獻(xiàn)[15]基于MAP準(zhǔn)則得到了Sage-Husa噪聲統(tǒng)計(jì)估值器，并給出了最優(yōu)MAP估值器、次優(yōu)MAP估值器、次優(yōu)無偏MAP估值器和時(shí)變?cè)肼暯y(tǒng)計(jì)估值器等多種形式。文獻(xiàn)[20]和文獻(xiàn)[21]分別將其拓展到UKF和CKF，給出了適用于UKF和CKF的遞推算法。由于UKF、CKF和CQKF同屬確定采樣型濾波器，借鑒UKF和CKF的遞推形式，得到如下適用于CQKF的次優(yōu)無偏MAP常值噪聲統(tǒng)計(jì)估計(jì)器：

(36)

(37)

(38)

(39)

對(duì)于時(shí)變?cè)肼暯y(tǒng)計(jì)而言，應(yīng)當(dāng)強(qiáng)調(diào)新近數(shù)據(jù)的作用，逐漸遺忘陳舊數(shù)據(jù)。選取加權(quán)系數(shù){γi}，使之滿足

(40)

于是有

(41)

式中：b為遺忘因子。將次優(yōu)無偏MAP常值噪聲統(tǒng)計(jì)估計(jì)器中的加權(quán)和系數(shù)1/k替換為{γi}，即得到適用于CQKF的時(shí)變?cè)肼暯y(tǒng)計(jì)估值器：

(42)

(43)

(44)

(45)

4 自適應(yīng)強(qiáng)跟蹤C(jī)QKF

將時(shí)變漸消因子和時(shí)變?cè)肼暯y(tǒng)計(jì)估值器嵌入標(biāo)準(zhǔn)CQKF，并將其拓展到噪聲均值非零的情形，即可得到AST-CQKF算法，流程如圖1所示。

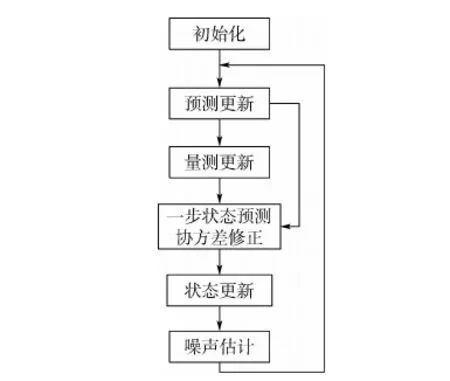
圖1 AST-CQKF算法流程圖Fig.1 AST-CQKF algorithm flowchart

算法具體流程如下：

步驟1初始化。

1) 令

2) 根據(jù)式(24)和式(25)計(jì)算CQ點(diǎn)ξl及對(duì)應(yīng)權(quán)值wl。

步驟2預(yù)測(cè)更新。

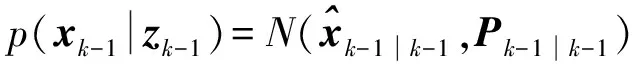
2) 計(jì)算CQ點(diǎn):

3) 計(jì)算CQ點(diǎn)隨狀態(tài)方程的轉(zhuǎn)移:

4) 計(jì)算一步狀態(tài)預(yù)測(cè)及預(yù)測(cè)誤差協(xié)方差矩陣：

步驟3量測(cè)更新。

1) 分解協(xié)方差矩陣:

2) 計(jì)算CQ點(diǎn):

3) 計(jì)算CQ點(diǎn)隨量測(cè)方程的轉(zhuǎn)移:

4) 計(jì)算量測(cè)預(yù)測(cè)值:

5) 計(jì)算自協(xié)方差矩陣和互協(xié)方差矩陣：

步驟4一步狀態(tài)預(yù)測(cè)協(xié)方差修正。

1) 根據(jù)式(35)計(jì)算漸消因子λk。

2) 利用λk修正一步狀態(tài)預(yù)測(cè)協(xié)方差矩陣：

3) 分解修正后的協(xié)方差矩陣：

4) 計(jì)算CQ點(diǎn)：

5) 計(jì)算CQ點(diǎn)經(jīng)量測(cè)方程的轉(zhuǎn)移:

6) 計(jì)算量測(cè)預(yù)測(cè)值:

7) 計(jì)算自協(xié)方差矩陣和互協(xié)方差矩陣:

步驟5狀態(tài)更新。

1) 計(jì)算卡爾曼增益：

2) 估計(jì)狀態(tài):

3) 估計(jì)狀態(tài)預(yù)測(cè)誤差協(xié)方差矩陣：

步驟6噪聲估計(jì)。

根據(jù)式(42)～式(45)對(duì)噪聲統(tǒng)計(jì)特性遞推估計(jì)。

5 仿真驗(yàn)證

考慮一個(gè)典型的二維平面雷達(dá)跟蹤問題[7]，目標(biāo)以固定未知轉(zhuǎn)彎速率Ω做圓周運(yùn)動(dòng),其狀態(tài)方程為

Xk-1+vk-1

(46)

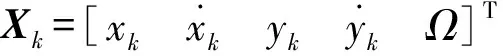
(47)

雷達(dá)固定于坐標(biāo)原點(diǎn)，對(duì)目標(biāo)的距離rk及方位角θk進(jìn)行測(cè)量，則量測(cè)方程為

(48)

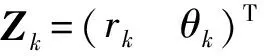
初始狀態(tài)真實(shí)值為

對(duì)應(yīng)的協(xié)方差矩陣為

P00= diag[100 m210 m2/s2100 m210 m2/s2

100 m·rad2/s2]T

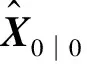
(49)

(50)

(51)

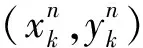
為驗(yàn)證算法在系統(tǒng)狀態(tài)模型不準(zhǔn)確及噪聲統(tǒng)計(jì)特性不準(zhǔn)確下的有效性，設(shè)置以下2種仿真情形。

5.1 系統(tǒng)量測(cè)噪聲的統(tǒng)計(jì)特性不準(zhǔn)確

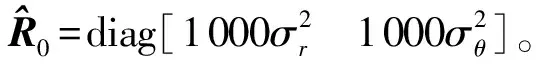
由圖2可知，通過AST-CQKF算法得到的位置、速度均方根誤差明顯小于CQKF算法，而轉(zhuǎn)彎率均方根誤差基本相同，可見AST-CQKF算法能夠有效減小噪聲統(tǒng)計(jì)特性不準(zhǔn)確帶來的估計(jì)誤差，提高估計(jì)精度。此外，噪聲統(tǒng)計(jì)特性的改變對(duì)位置、速度、轉(zhuǎn)彎率的影響程度不同，對(duì)位置影響最大，速度次之，轉(zhuǎn)彎率幾乎無影響。

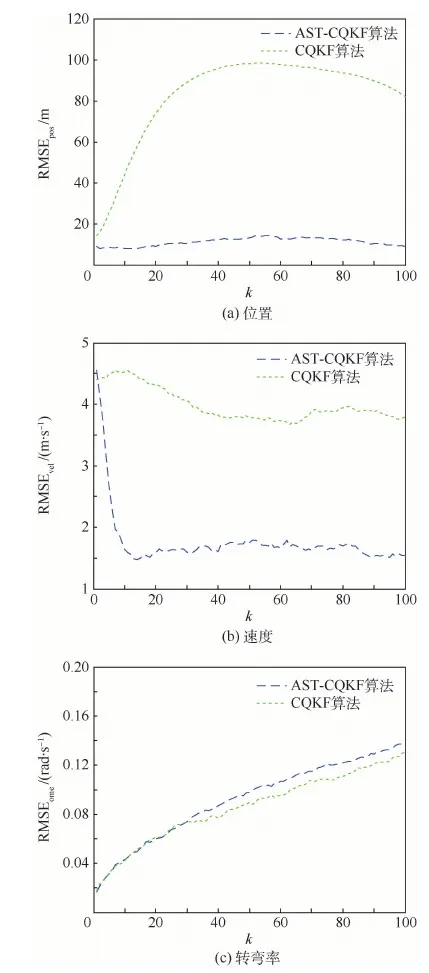
圖2 跟蹤均方根誤差(情形1)Fig.2 RMSE tracking(Case 1)

5.2 系統(tǒng)狀態(tài)模型不準(zhǔn)確

為設(shè)置系統(tǒng)模型的不確定性，將式(46)變形得

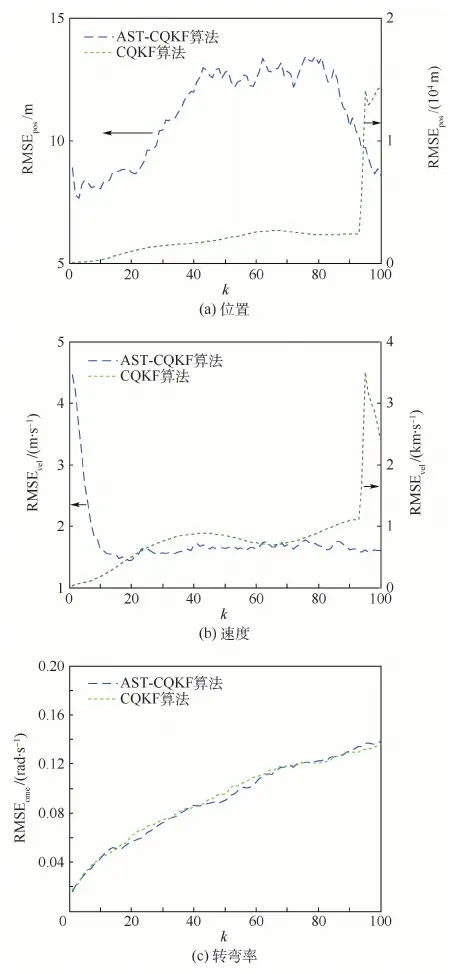
圖3 跟蹤均方根誤差(情形2)Fig.3 RMSE tracking(Case 2)

Xk=

Xk-1+vk-1

(52)

式中：a和c為可調(diào)節(jié)的參數(shù)，模型正常時(shí)兩者均為1，通過設(shè)置不同的系數(shù)以模擬系統(tǒng)狀態(tài)模型的不確定性，本文設(shè)定a=1.1，c=1.2。仿真過程中，狀態(tài)真值由精確的狀態(tài)方程得到，而濾波器使用不精確的狀態(tài)方程進(jìn)行狀態(tài)估計(jì)，以此比較AST-CQKF與CQKF算法在系統(tǒng)狀態(tài)模型不準(zhǔn)確時(shí)的濾波精度。經(jīng)過200次獨(dú)立的蒙特卡羅仿真，得到位置、速度、轉(zhuǎn)彎率的RMSE結(jié)果分別如圖3所示(情形2)。

由圖3可知，系統(tǒng)狀態(tài)模型不準(zhǔn)確時(shí)，CQKF在仿真開始后迅速發(fā)散，無法對(duì)目標(biāo)保持跟蹤，而AST-CQKF算法雖然不能完全消除模型不確定性的影響，但能夠防止濾波發(fā)散，保持濾波收斂性，對(duì)于模型不確定型具有魯棒性。

設(shè)置不同的仿真步數(shù)與仿真次數(shù)，得到CQKF算法與AST-CQKF算法的仿真計(jì)算時(shí)間如表1所示。由表1可以看出，與前者相比，后者的仿真計(jì)算時(shí)間增加了一倍左右，尤其是仿真次數(shù)較多時(shí)，計(jì)算時(shí)間的增加更為明顯，這是由于AST-CQKF算法步驟更多、復(fù)雜度更高引起的。但單次仿真時(shí)，2種算法的時(shí)間均小于0.1 s，因此與濾波精度的提高相比，AST-CQKF算法的時(shí)間增加處于可接受的范圍內(nèi)。

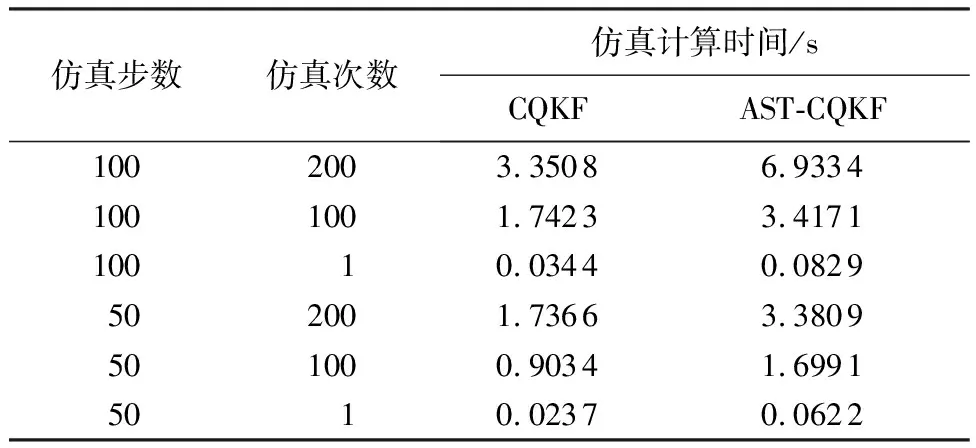
表1 CQKF與AST-CQKF算法蒙特卡羅仿真計(jì)算時(shí)間Table 1 Calculation time of Monte Carlo simulation in CQKF and AST-CQKF algorithm

6 結(jié) 論

CQKF算法在復(fù)雜對(duì)抗環(huán)境下的目標(biāo)跟蹤主要存在2方面問題：①系統(tǒng)狀態(tài)空間模型發(fā)生突變導(dǎo)致濾波發(fā)散；②噪聲統(tǒng)計(jì)特性發(fā)生改變或不精確造成濾波精度下降。針對(duì)該問題，本文提出了一種新的自適應(yīng)強(qiáng)跟蹤C(jī)QKF(AST-CQKF)算法應(yīng)用到目標(biāo)跟蹤：

1) 將強(qiáng)跟蹤濾波器與CQKF相結(jié)合，給出了適用于CQKF的漸消因子計(jì)算方法，利用漸消因子修正一步狀態(tài)預(yù)測(cè)協(xié)方差矩陣，進(jìn)而用于狀態(tài)估計(jì)，克服了模型不準(zhǔn)確影響濾波精度和濾波穩(wěn)定性的問題，改善了CQKF的跟蹤性能。

2) 利用Sage-Husa時(shí)變?cè)肼暯y(tǒng)計(jì)估值器對(duì)噪聲實(shí)時(shí)估計(jì)，得到了AST-CQKF算法，增強(qiáng)了濾波器對(duì)于噪聲統(tǒng)計(jì)特性變化的自適應(yīng)能力，有效地提高了濾波精度。

3) 仿真結(jié)果表明，在系統(tǒng)量測(cè)噪聲統(tǒng)計(jì)特性不準(zhǔn)確或狀態(tài)空間模型不準(zhǔn)確的情況下，CQKF算法的濾波精度急劇下降甚至濾波發(fā)散， AST-CQKF算法則能夠?qū)崿F(xiàn)系統(tǒng)狀態(tài)的快速準(zhǔn)確跟蹤，有效地克服了CQKF算法的局限性。

參考文獻(xiàn) (References)

[1] KALMAN R E.A new approach to linear filtering and prediction theory[J].Transactions on ASME Journal of Basic Engineering,1960,82(D):35-46.

[2] JAZWINSKI A H.Stochastic processes and filtering theory[M].New York:Academic Press,1970:235-237.

[3] 李天成,范紅旗.孫樹棟.粒子濾波理論、方法及其在多目標(biāo)跟蹤中的應(yīng)用[J].自動(dòng)化學(xué)報(bào),2015,41(12):1981-2002.

LI T C,FAN H Q,SUN S D.Particle filtering:Theory,approach,and application for multitar-get tracking[J].Acta Automatica Sinica,2015,41(12):1981-2002(in Chinese).

[4] 韓萍,干浩亮,何煒琨,等.基于迭代中心差分卡爾曼濾波的飛機(jī)姿態(tài)估計(jì)[J].儀器儀表學(xué)報(bào),2015,36(1):187-193.

HAN P,GAN H L,HE W K,et al.Iterated central difference Kalman filter based aircraft attitude estimation[J].Chinese Journal of Scientific Instrument,2015,36(1):187-193(in Chinese).

[5] 王寶寶，吳盤龍. 基于平方根無跡卡爾曼濾波平滑算法的水下純方位目標(biāo)跟蹤[J].中國(guó)慣性技術(shù)學(xué)報(bào),2016,24(2):180-184.

WANG B B,WU P L.Underwater bearing-only tracking based on square-root unscented Kalman filter smoothing algorithm[J].Journal of Chinese Inertial Technology,2016,24(2):180-184(in Chinese).

[6] 張龍,崔乃剛,楊峰,等.高階容積卡爾曼濾波及其在目標(biāo)跟蹤中的應(yīng)用[J].哈爾濱工程大學(xué)學(xué)報(bào),2016,37(4):573-578.

ZHANG L,CUI N G,YANG F,et al.High-degree cubature Kalman filter and its application in target tracking[J].Journal of Harbin Engineering University,2016,37(4):573-578(in Chinese).

[7] BHAUMIK S,WATI S.Cubature quarature Kalman filter[J]. IET Signal Processing,2013,7(7):533-541.

[8] LAINIOTIS D G.Optimal adaptive estimation:Structure and parameters adaption[J].IEEE Transactions on Automatic Control,1971,16(2):160-170.

[9] MEHRA R K. On the identification of variances and adaptive filtering[J].IEEE Transactions on Automatic Control,1970,15(2):175-184.

[10] ODELSON B J,RAJAMANI M R,RAWLINGS J B.A new autocovariance least-squares method for estimating noise covariances[J].Automatica, 2006,42(2):303-308.

[11] AKESSON B M,JORGENSON J B,POULSEN N K,et al.A generalized autocovariance least-squares method for Kalman filter tuning[J].Journal of Process Control,2008,18(7-8):769-779.

[12] MYERS K A,TAPLEY B D.Adaptive sequential estimation with unknown noise statistics[J].IEEE Transactions on Automatic Control,1976,21(8):520-523.

[13] KASHYAP R L.Maximum likelihood identification of stochastic linear systems[J].IEEE Transactions on Automatic Control,1970,15(1):25-34.

[14] LIMA F V, RAJAMANI M R, SODERSTROM T A,et al.Covariance and state estimation of weakly observable systems:Application to polymerization processes[J].IEEE Transactions on Control Systems Technology,2013,21(4):1249-1257.

[15] 李寧,祝瑞輝,張勇剛.基于Sage-Husa算法的自適應(yīng)平方根CKF目標(biāo)跟蹤方法[J].系統(tǒng)工程與電子技術(shù),2014,36(10):1899-1905.

LI N,ZHU R H,ZHANG Y G.Adaptive square CKF method for target tracking based on Sage-Husa algorithm[J].Systems Engineering and Electronics,2014,36(10):1899-1905(in Chinese).

[16] 王小旭,潘泉,黃鶴,等.非線性系統(tǒng)確定采樣型濾波算法綜述[J].控制與決策,2012,27(6):801-812.

WANG X X,PAN Q,HUANG H,et al.Overview of deterministic sampling filtering algorithms for nonlinear system[J].Control and Decision,2012,27(6):801-812(in Chinese).

[17] 周東華，席裕庚，張鐘俊.一種帶多重次優(yōu)漸消因子的擴(kuò)展卡爾曼濾波器[J].自動(dòng)化學(xué)報(bào),1991,17(6):689-695.

ZHANG D H,XI Y G,ZHANG Z J.A suboptimal multiple fading extended Kalman filter[J].Acta Automatica Sinica, 1991,17(6):689-695(in Chinese).

[18] 方君,戴邵武,許文明,等.基于ST-SRCKF的超高速強(qiáng)機(jī)動(dòng)目標(biāo)跟蹤算法[J].北京航空航天大學(xué)學(xué)報(bào),2016,42(8):1698-1708.

FANG J,DAI S W,XU W M,et al.Highly maneuvering hypervelocity-target tracking algorithm based on ST-SRCKF[J].Journal of Beijing University of Aeronautics and Astronautics,2016,42(8):1698-1708(in Chinese).

[19] 張龍,崔乃剛,王小剛,等.強(qiáng)跟蹤-容積卡爾曼濾波在彈道式再入目標(biāo)跟蹤中的應(yīng)用[J].中國(guó)慣性技術(shù)學(xué)報(bào),2015,23(2):211-218.

ZHANG L,CUI N G,WANG X G,et al.Strong tracking-cubature Kalman filter for tracking ballistic reentry target[J].Journal of Chinese Inertial Technology,2015,23(2):211-218(in Chinese).

[20] 趙琳,王小旭,孫明,等.基于極大后驗(yàn)估計(jì)和指數(shù)加權(quán)的自適應(yīng)UKF濾波算法[J].自動(dòng)化學(xué)報(bào),2010,36(7):1007-1019.

ZHAO L,WANG X X,SUN M,et al.Adaptive UKF filteing algorithm based on maximum a posterior estimation and exponential weighting[J].Acta Automatica Sinica,2010,36(7):1007-1019(in Chinese).

[21] 丁家琳,肖建,趙濤.自適應(yīng)CKF強(qiáng)跟蹤濾波器及其應(yīng)用[J].電機(jī)與控制學(xué)報(bào),2015,19(11):111-120.

DING J L,XIAO J,ZHAO T.Adaptive CKF strong tracking filter and application[J].Electric Machines and Control,2015,19(11):111-120(in Chinese).