三款動態數學軟件設計“迭代”類積件的比較分析*
——以《圓的面積》公式推導為例
☆ 楊秀燕 黃立春 唐劍嵐
(廣西師范大學數學與統計學院,廣西桂林 541004)
迭代是一種類似于程序設計中遞歸算法的特殊變換,是指按照一定的變換規則,由原象(發生迭代的初始對象)到初象(原象經過一系列變換操作得來的對象)反復映射的過程。原象可以是進行幾何迭代的點,也可以是進行數值迭代的參數。
一、積件基本原理及效果
《圓的面積》是人教版六年級上冊第五章的內容,在圓的面積公式的推導中滲透“轉化思想”、“圖形的割補”、“化曲為直”、“無限逼近”等數學思想與方法,有助于發展學生的空間觀念和推理能力。
引入動態數學軟件一方面是為了增強課堂互動性,另一方面旨在通過積件,動態視覺化的呈現圓切割并拼接成矩形的過程,從而突破圓的面積公式推導的難點,提效課堂教學。積件首先呈現半徑為r且切割成若干等份的圓(如圖1);接著,將上、下部分扇形展開至同一水平線并拼接成矩形(或平行四邊形),其中矩形的高近似圓的半徑r,底近似圓周長的一半;最后,增加分割份數,得出矩形面積,從而推出圓的面積計算公式。

圖1 圓的面積積件展示
一般而言,考慮將上、下半圓分成N等分,總體上為2N等分。N為奇數或偶數影響制作過程。首先,考慮當N為偶數時。在圓展開至同一水平線過程中,可以發現,各扇形上的弦與水平方向夾角逐漸減小,直至水平時夾角為0度。考慮四分之一圓(如圖2),圓弧展開動畫實質上經歷了(1)Rotate({S4},P4,α)(表示扇形S4繞著點P4旋轉α,α>0時逆時針方向旋轉);(2)Rotate({S3,S4},P3,α);(3)Rotate({S2,S3,S4},P2,α);(4)Rotate({S1,S2,S3,S4},P1,α/2)。 其中α為等分后扇形的圓心角,值為180°/N,值得注意的是,弦P1P2在半徑OP1上的弦切角僅為扇形所對的圓心角的一半。因此,上述(4)的旋轉角為α/2。
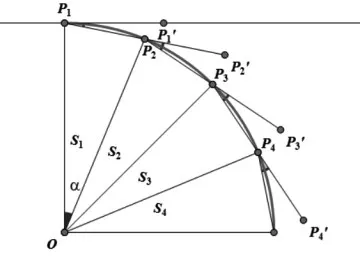
圖2 N為偶數

圖3 N為奇數
由上分析可得,對四分之一圓n等分,展開動畫為
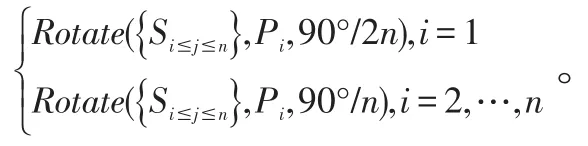
接著,分析當N為奇數時。在四分之一圓中(如圖3),發 生(1)Rotate({S3},P3,α);(2)Rotate({S2,S3},P2,α);(3)Rotate({S1,S2,S3},P1,α)。與N為偶數的區別在于不存在旋轉角為α/2的情況。如下以N為偶數為例,分別應用三款軟件實現圓的分割。
二、三款軟件的制作過程
三款軟件均能夠動態地展現出幾何對象的位置關系、運行變化規律。但是,操作過程與動畫原理之間存在一定的差異性。
(一)幾何畫板制作過程
20世紀80年代幾何畫板由美國Key Curriculum Press公司制作并出版,1996年該公司授權人民教育出版社在中國發行該軟件的中文版。強大的迭代功能是幾何畫板制作本積件的優勢所在,特別是能夠支持參數與幾何的同步迭代,為本積件的制作帶來了便利。具體制作過程如下。
1.創建控制點以及參數
繪制點A(1,0)與B(1,-1),選中點O(原點)、A、B構造“三角形的內部”,并在三角形上取“邊界上的點”,得點C,作為控制點;度量點C的橫與縱坐標,新建參數t=1與 N=4;依次計算“abs(yc)”、“t=1”、“N-1”、“-90°/N”、“-90°/2N”、“90°(sgn(t-1)+1)/2/N·xc”。
2.確定半徑以及制作拼接動畫
在y軸上取點D,雙擊O標記中心,按固定比1/2縮放D得到點E;以O為中心,“-90°/2N”為旋轉角,旋轉E得到點E′;以D為中心,縮放E′固定比-yc/2得到點F;標記向量DO,平移F得到點F′。其中點D用于控制圓的半徑大小。
3.制作迭代原像
在畫布上任意畫G、H兩點,以G為中心,最后一個參數為旋轉角度(如圖4),旋轉H得到點H′;再以H′為中心,“-90°/N”為旋轉角,旋轉G得到點 G′;連接線段FF′,雙擊線段FF′標記鏡面,反射如圖5所示扇形(包括線段GH′、G′H′、弧 GG′以及面 GG′H′);再以O為中心,將兩扇形旋轉180°。
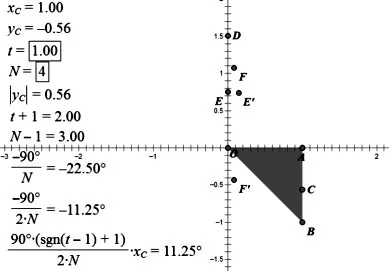
圖4 幾何畫板各參數

圖5 迭代原像
4.深度迭代
依次選中G、H、t以及N-1,按住Shift鍵不放,選擇深度迭代,創建 (G,H,t)→(G′,H′,t+1)的迭代;選中點G和F,單擊“編輯/合并”,重復操作,將點H和F′也合并。
5.優化界面
隱藏無關對象,分別制作C到A、B、O的移動按鈕,添加文本等。此時已實現“化圓為方”效果,其中底邊長為周長的一半πr,高為半徑r。
(二)Hawgent皓駿制作過程
Hawgent皓駿是一款動態數學軟件,能夠處理幾何、代數、三角、概率、統計、算法、微積分等數學問題,并且能夠根據圖形間的邏輯關系推理出幾何性質,即自助推理。Hawgent皓駿同樣具備迭代功能,雖然當前版本不能實現參數與幾何圖形的同步迭代(數值迭代中的參數能在幾何迭代中直接應用),在本案例中無法判斷旋轉角為α還是α/2,但也可以通過其他操作達到目的。其具體實現方法如下。
在此之前,有必要說明:Hawgent皓駿測量值或計算值按照創建順序默認給參數賦予u000-u999形式的變量名,引用參數時只需手動輸入參數的變量名即可。
1.創建控制點以及參數
顯示坐標系,繪制點A(0,0)、B(1,0)、C(1,-1);依次選中A、B、C創建多邊形,在多邊形上取點D;測量D的X-坐標XD與y-坐標yD,此時XD、yD變量名分別為u000、u001;創建變量尺,其中變量名為n,范圍為2到10,計算“ -90/floor(n)”。
2.確定半徑并制作拼接動畫
在y軸上取點E,依次選中A、E,創建中點F;依次選中F、A,構造旋轉變化旋轉“u002/2”得到點G;依次選中E、G,創建參數為“-u001”的參數點H;依次選中H、E、A,構造平移變換得到點I,線段連接HI。
3.制作迭代原像與初像
依次選中I、H,構造旋轉變換旋轉“-u000*u002/2”得到點J;依次選中H、J,構造旋轉變換旋轉“u002”得到點K;依次選中點H、J,繪制指定圓心角的圓弧,其中圓心角為“u002 ”;連接線段HJ、KJ;重復上述操作,J繞 K旋轉“-u000*u002”得到點L,然后K繞L旋轉“u002”得到點M,創建圓弧連接線段。
4.迭代變換
依次選中J、K,單擊迭代打開迭代窗口,新建(J,K)→(L,M)映射,勾選顯示弧以及扇形的兩條邊,確定迭代。此時默認做5次,激活編輯模式,在對象窗口中找到迭代,右鍵打開迭代屬性窗口,修改迭代層數為“floor(n)-2”。
5.完善圖形優化界面
選中所有扇形以及線段HI,構造對稱變換;再次選中所有扇形以及點A,構造旋轉變換旋轉180°;選中點D創建變量尺,隱藏無關變量,填充扇形顏色等(如圖6)。
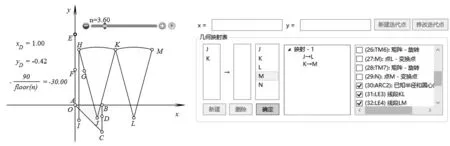
圖6 Hawgent皓駿
(三)玲瓏畫板制作過程
經過多年的探索與更新,玲瓏畫板在平面幾何、立體幾何、解析幾何、不等式、函數等領域應用廣泛。特別是在立體幾何上有著不錯的表現,立體圖形的創建、空間動畫制作等均有所突破。遺憾的是,玲瓏畫板當前版本缺失迭代功能。所以在本案例中,只能制作確定切割份數的積件,具體制作過程如下。
1.等分圓以及創建參數
右鍵選擇“2D網格模式”,在網格上繪制半徑為4且第二個點位于圓心的正右側位置的圓,然后隱藏網格;自左向右用線段連接圓心與圓上的點,并在線段上取一點A;新建參數a,雙擊參數,選中線段上的點,修改終值為0.5,最大值為30,選中點A綁定動點。此時點A在0到0.5位置上移動時參數a的變化范圍是0到30。
2.制作展開動畫
將圓12等分,對點添加標簽;單擊“創建—變換—旋轉”打開旋轉變換窗口,首先以點P3為中心,旋轉角度為a,將P4與O添加變換得到點O1和P5;然后再以P2為中心,旋轉角度為a,將對P3、O以及O1、P5添加變換得到點 O2、O3、P6、P7;最后再以P1為中心,旋轉a/2角度,將P2、O、O2、O3、P6、P7添加變換得到點 O4、O5、O6、P8、P9、P10。由于過程中涉及的點過多,可選擇性的將不需要的點隱藏。
3.補充其余展開動畫
連接OP1并作其中點B,選中點B,以O旋轉中心,旋轉角度為-15°,添加變換得到點B′;連接OB′,在O點上新建自由點O′;打開平移動畫窗口,選中點A設定變量(拖動A可以實現動畫過程),選中OB′設定平移軸,修改起值為0.5終值為1,將O′添加到動畫;以OP1為旋轉軸,旋轉角度為180°,對各扇形上的點添加變換;最后再以O′為中心,旋轉角度為180°,對各扇形上的點添加變換。如此即可補充其余部分圓上的展開動畫。
4.優化界面
將各扇形圓弧補充完整,并創建“圓弧面”;修改顏色,隱藏無關對象等(如圖7)。

圖7 玲瓏畫板
三、總結與思考
Hawgent皓駿與玲瓏畫板是國內新興的動態數學軟件,較之幾何畫板或許不夠成熟,但也各具千秋。對比發現,幾何畫板的迭代功能較強,能支持幾何與數值的同步迭代。而Hawgent皓駿的幾何迭代與數值迭代雖然分開進行,但也能實現較好的迭代功能。玲瓏畫板目前還不能很好的支持迭代,于本案例而言,幾何畫板更具優勢。
在實際教學中,教師可根據教學需求選擇合適的軟件。當然,技術的使用是手段而不是目的。如果使用得當,將技術有機融入數學教學中,幫助學生理解數學,提高學生的學習興趣,改善學習方式,將能在“授人以魚”的同時“授人以漁與欲”。
[1]唐劍嵐等主編.計算機輔助數學教學原理與實踐[M].北京:清華大學出版社,2012.
[2]唐劍嵐,莊麗薇.優化圓的面積公式推導的課件設計[J].中小學電教,2011(10):64-66.
[3]張景中,彭翕成.三款數學教育軟件的比較與設計思想分析[J].中國電化教育,2010(01):107-113.
[4]張景中,彭翕成.函數作圖軟件的評價和選擇[J].數學通報,2007(08):1-9.
[5]唐劍嵐.魚漁欲”三位一體優化數學教學的理念與策略—以“三角形的內角”課例片段分析為例[J].基礎教育研究,2015(09):5-10.
[6]唐劍嵐,周元.授人以魚”的同時“授人以漁與欲”—以《等差數列的前n項和》公式推導片段為例[J].數學通報,2016(09):41-46.

