一個(gè)常見(jiàn)平面幾何題的拓展與應(yīng)用*

● ●

(杭州市基礎(chǔ)教育研究室,浙江 杭州 310003) (青春中學(xué)，浙江 杭州 310006)

“杭州市初中數(shù)學(xué)青年教師核心組”QQ群，從2018年1月3日開(kāi)始在每周三和周日定時(shí)舉行網(wǎng)絡(luò)在線(xiàn)解題研究討論，40余位成員輪流主持．1月3日討論的是一道大家非常熟悉的平面幾何問(wèn)題，歷時(shí)3小時(shí)的討論，大家給出原題的多種不同解法以及多角度的推廣，追本溯源地發(fā)現(xiàn)問(wèn)題背后的本質(zhì)，并給出向量意義下的進(jìn)一步推廣，以及發(fā)現(xiàn)了部分結(jié)論與常見(jiàn)問(wèn)題的聯(lián)系．討論結(jié)束后大家一致認(rèn)為收獲滿(mǎn)滿(mǎn)，筆者將討論的結(jié)果整理出來(lái)與廣大初中數(shù)學(xué)教師分享．

1 原題呈現(xiàn)

當(dāng)我們遇到熟悉的數(shù)學(xué)問(wèn)題時(shí)，往往會(huì)受思維定勢(shì)的影響，用自己熟悉的方法快速解決問(wèn)題．殊不知，這時(shí)我們已經(jīng)失去了對(duì)這個(gè)問(wèn)題做進(jìn)一步研究的機(jī)會(huì)．有時(shí)，對(duì)于這樣的問(wèn)題，重新回味一下，靜下心來(lái)細(xì)細(xì)思考，會(huì)有新的收獲．

原題呈現(xiàn)點(diǎn)P是矩形ABCD內(nèi)一點(diǎn)，若AP=3，DP=2，CP=5,求BP的長(zhǎng)．

解法1如圖1，過(guò)點(diǎn)P作EF∥AB，分別交AD，BC于點(diǎn)E，F(xiàn)．設(shè)AE=a，DE=b，EP=c，F(xiàn)P=d，易證

a2+c2=9，

(1)

b2+c2=4,

(2)

b2+d2=25,

(3)

式(1)+式(3)-式(2)，得

a2+d2=30，

即

BP2=30.

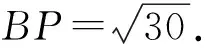
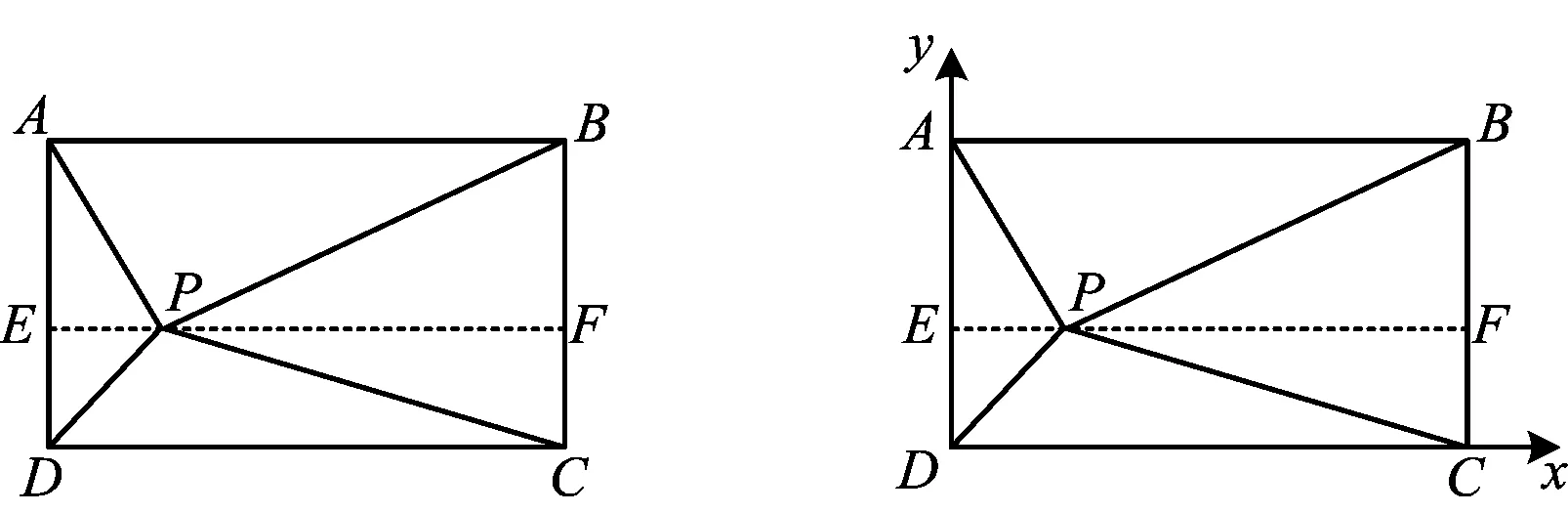
圖1 圖2

解法2如圖2，以點(diǎn)D為坐標(biāo)原點(diǎn)、分別以DC，DA所在的直線(xiàn)為x軸和y軸建立直角坐標(biāo)系．設(shè)DA=a，DC=b，則A(0，a)，B(b，a)，C(b，0)，P(x，y)，從而

與解法1類(lèi)似可得

(x-a)2+(y-b)2=30,

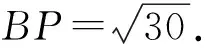
兩種解法的共同點(diǎn)是：線(xiàn)段BP的長(zhǎng)并不依賴(lài)矩形的形狀，與矩形的邊長(zhǎng)也不構(gòu)成直接相關(guān)，這引發(fā)了大家的關(guān)注和熱烈討論．以下是筆者根據(jù)討論的內(nèi)容整理而成的，為呈現(xiàn)一定的研究邏輯，在問(wèn)題呈現(xiàn)的順序上做了一定的調(diào)整．

2 相關(guān)研究

為了對(duì)原題作深入研究，給出以下4個(gè)命題，其中命題1是命題2的特例，命題3是命題2的逆命題，命題4即原題的推廣．

命題1三角形相鄰兩邊的平方差等于這兩邊在第三邊上的射影的平方差．

如圖3，在△ABC中，AD⊥BC于點(diǎn)D，則

AB2-AC2=BD2-DC2.

顯然，根據(jù)勾股定理可得

AD2=AB2-BD2，AD2=AC2-DC2，

從而

AB2-BD2=AC2-DC2，

移項(xiàng)整理得AB2-AC2=BD2-DC2,

故命題1成立．

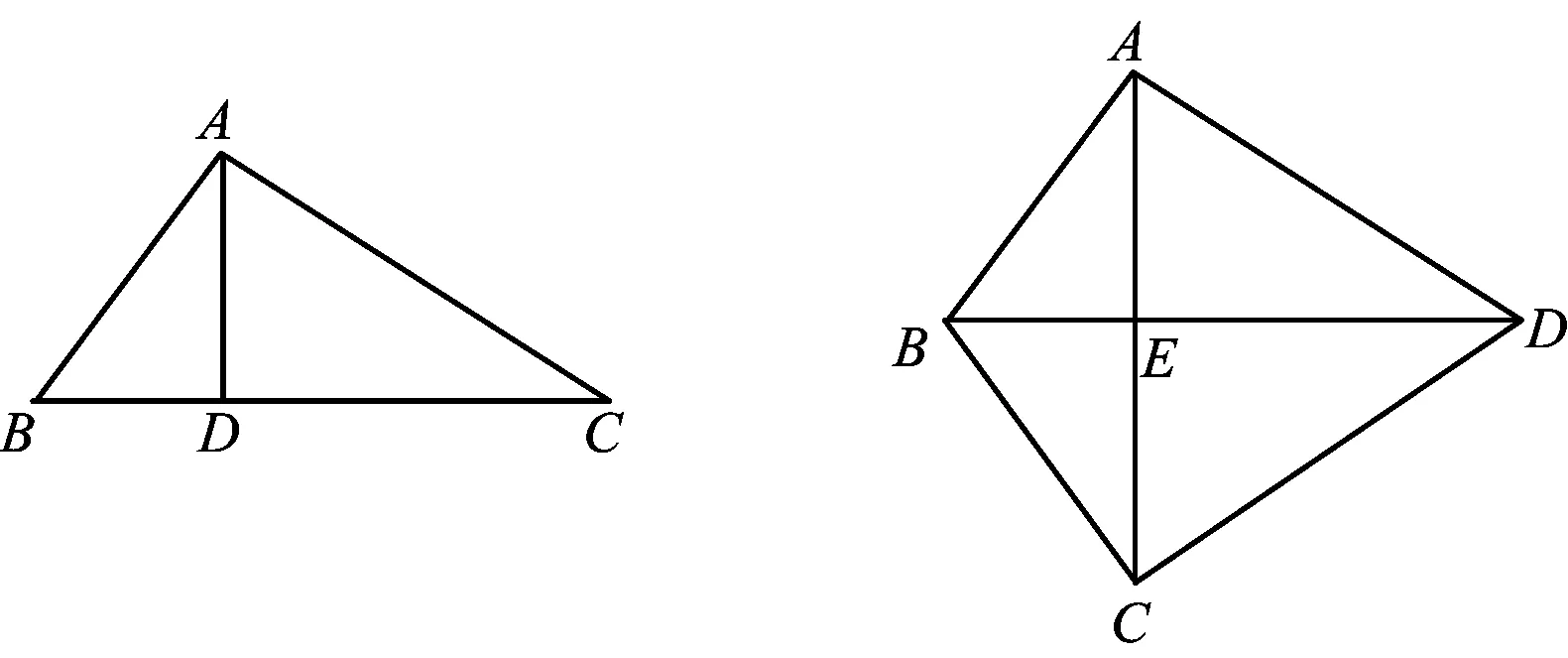
圖3 圖4

命題2對(duì)角線(xiàn)互相垂直的四邊形的對(duì)邊的平方和相等．

如圖4，若四邊形ABCD的對(duì)角線(xiàn)AC⊥BD，則

AB2+CD2=BC2+AD2．

顯然，根據(jù)命題1可得

AB2-AD2=BE2-ED2，

BC2-CD2=BE2-ED2，

從而

AB2-AD2=BC2-CD2，

移項(xiàng)即得

AB2+CD2=BC2+AD2,

故命題2成立．

命題2的逆命題(命題3)是否成立呢？

命題3對(duì)邊平方和相等的四邊形的對(duì)角線(xiàn)互相垂直．

如圖4，設(shè)四邊形ABCD的對(duì)角線(xiàn)AC，BD相交于點(diǎn)E，若AB2+CD2=BC2+AD2，則AC⊥BD．

證明因?yàn)?/p>

AB2+CD2-BC2-AD2=

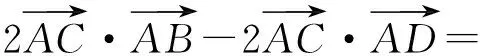
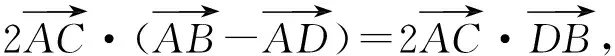
又

AB2+CD2=BC2+AD2，

所以

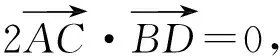
從而

AC⊥BD,

故命題3成立．

進(jìn)一步研究表明，原題可推廣得更一般的結(jié)論：

命題4(原題推廣)若點(diǎn)P是矩形ABCD內(nèi)一點(diǎn)，則PA2+PC2=PB2+PD2．

證法1如圖5，過(guò)點(diǎn)P作EF∥AB交AD，BC于點(diǎn)E,F,根據(jù)命題1得

PA2-PD2=AE2-ED2=BF2-CF2=

(BF2+FP2)-(CF2+FP2)=

PB2-PC2．

移項(xiàng)即得PA2+PC2=PB2+PD2．

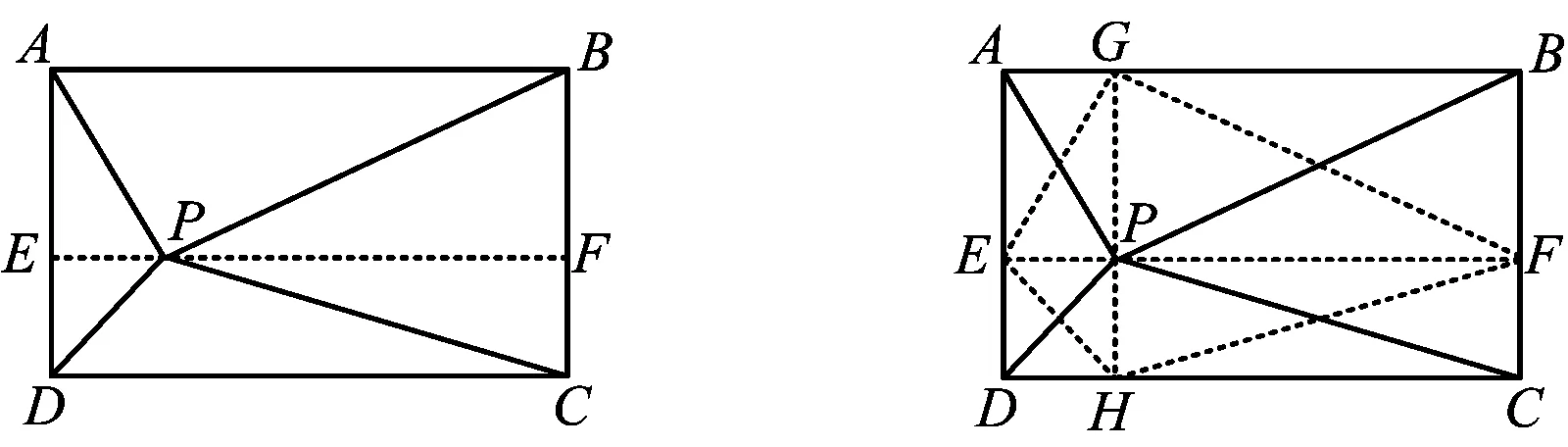
圖5 圖6

證法2(通過(guò)構(gòu)造，進(jìn)行證明)如圖6，過(guò)點(diǎn)P作線(xiàn)段GH，EF分別垂直于矩形的對(duì)邊，則GH⊥EF．

聯(lián)結(jié)EG，GF，F(xiàn)H，HE，則四邊形EGFH為對(duì)角線(xiàn)互相垂直的四邊形，根據(jù)命題2，得

EG2+FH2=EH2+GF2.

又因?yàn)?個(gè)小矩形的對(duì)角線(xiàn)相等，即

EG=PA，GF=PB，F(xiàn)H=PC，EH=PD，

所以

PA2+PC2=PB2+PD2．

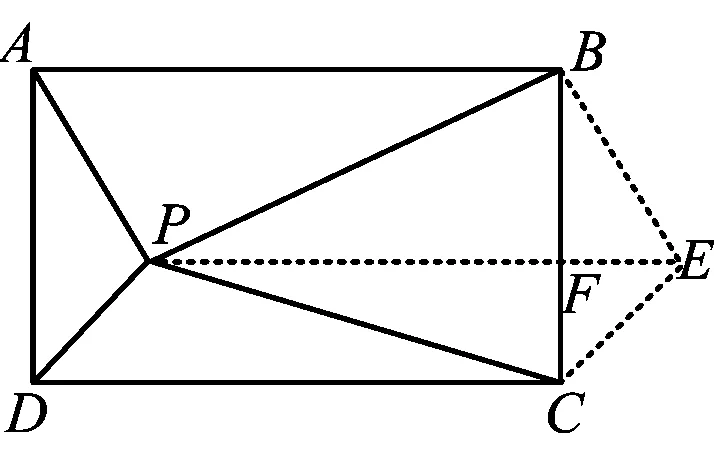
圖7

證法3如圖7，構(gòu)造與證法2類(lèi)似的證明，請(qǐng)讀者自己完成．

這里給出的3種證法，本質(zhì)上都是構(gòu)造直角三角形，利用勾股定理得到線(xiàn)段之間的關(guān)系，體現(xiàn)了歐氏幾何中研究定量問(wèn)題的一般方法．

事實(shí)上，若點(diǎn)P是空間中任意一點(diǎn)，本題的結(jié)論仍舊成立．

3 追本溯源

命題4的逆命題成立嗎？

命題5設(shè)P為四邊形ABCD內(nèi)一點(diǎn)，若PA2+PC2=PB2+PD2，則四邊形ABCD是矩形．

顯然，當(dāng)PA，PB，PC，PD都相等時(shí)，點(diǎn)A，B，C，D在同一個(gè)⊙P上，滿(mǎn)足PA2+PC2=PB2+PD2，此時(shí)四邊形ABCD的形狀并不不確定；當(dāng)PA，PB，PC，PD不全相等時(shí)，即使點(diǎn)A，B，C位置固定不變，滿(mǎn)足條件的點(diǎn)D也可以落在以P為圓心、PD為半徑的圓上，位置也不固定，由此，四邊形的形狀也不一定是矩形．因此，命題5是假命題．

如果把原題改變成下面的形式出現(xiàn)，似乎更不容易解決了．

如圖8，一組同心圓O，半徑分別為2，3，5，記作⊙O1，⊙O2，⊙O3．點(diǎn)A，B分別在⊙O1，⊙O2上，過(guò)點(diǎn)B作AB的垂線(xiàn)，與⊙O3有兩個(gè)交點(diǎn)，任取一個(gè)交點(diǎn)記作點(diǎn)C，分別過(guò)點(diǎn)A，C作AB，BC的垂線(xiàn)，交于點(diǎn)D．求證：點(diǎn)D必在⊙O的一個(gè)同心圓上．

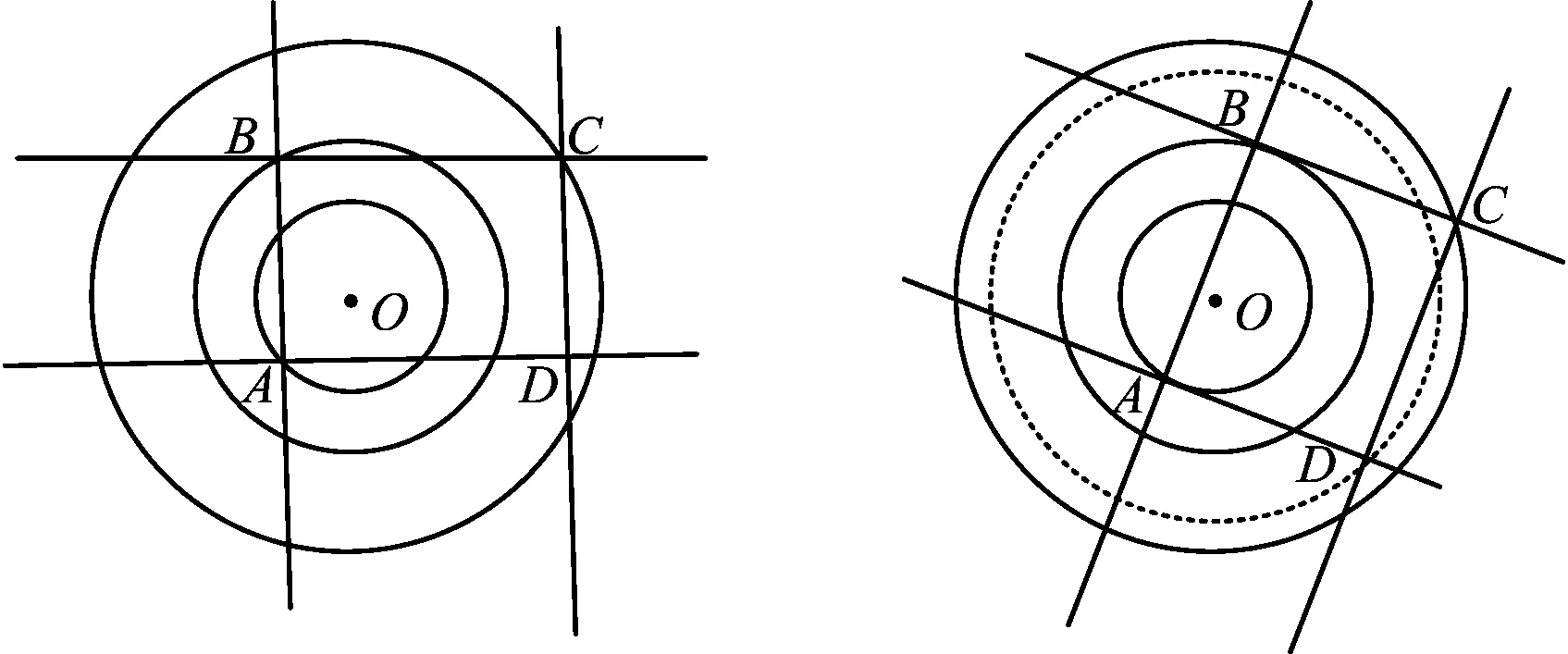
圖8 圖9

下面給出能揭示問(wèn)題本源的證明：

證法4如圖10，根據(jù)三角形中線(xiàn)公式，得

顯然，AC=BD，從而

PA2+PC2=PB2+PD2．

在△APC和△BPD中，因?yàn)橛辛司匦芜@個(gè)大前提，所以AC=BD始終成立．對(duì)于符合題意的任意矩形中的點(diǎn)P，到矩形中心O的連線(xiàn)段PO是兩個(gè)三角形公共的中線(xiàn).由三角形中線(xiàn)公式，把PA2+PC2和PB2+PD2轉(zhuǎn)化為矩形對(duì)角線(xiàn)與PO之間的關(guān)系，不變性就一目了然了．

顯然，從該證明中可以看出，矩形ABCD的形狀可以隨著AC和BD的夾角而變化．當(dāng)線(xiàn)段AC和BD隨點(diǎn)O旋轉(zhuǎn)時(shí)(或變成空間問(wèn)題)，結(jié)論都成立．

4 再次推廣

如果把結(jié)論推廣到平行四邊形中會(huì)得到什么結(jié)論？利用剛才的思路，這個(gè)問(wèn)題就變得很清晰了．

推廣1若點(diǎn)P為ABCD內(nèi)任意一點(diǎn)，則

證明如圖11，分別聯(lián)結(jié)兩條對(duì)角線(xiàn)，交于點(diǎn)O，則

證明過(guò)程中使用了向量中的常見(jiàn)恒等式:

4a·b=(a+b)2-(a-b)2．

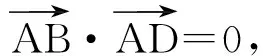
5 簡(jiǎn)單應(yīng)用

例1已知△ABC是等腰三角形，AB=AC，D在線(xiàn)段BC上，求證：AB2-AD2=BD·DC．

證明如圖12，過(guò)點(diǎn)A作AE⊥BC于點(diǎn)E，則根據(jù)命題1，有

AB2-AD2=BE2-DE2=

(BE-DE)·(BE+DE)=BD·DC．

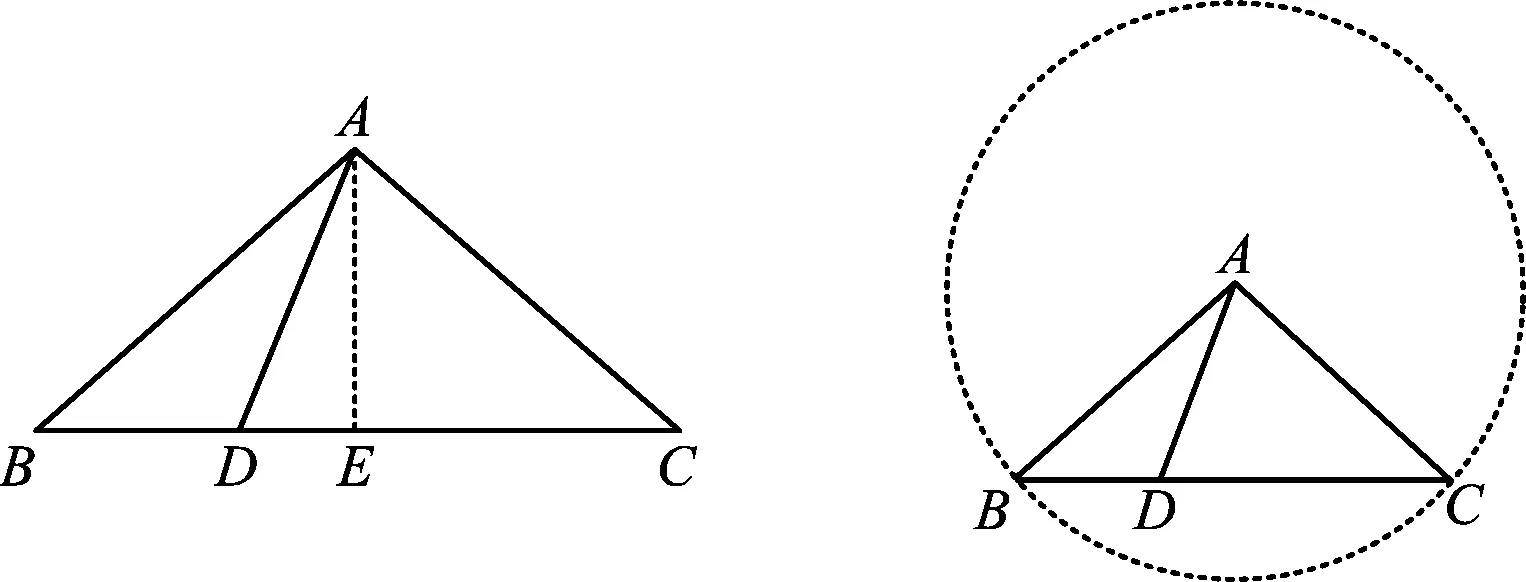
圖12 圖13

拓展1如圖13，如果畫(huà)出△ABC的外接圓⊙A，設(shè)半徑為r，AD=d，則上式可改寫(xiě)為

BD·DC=r2-d2．

這就是相交弦定理，當(dāng)D為線(xiàn)段BC的外分點(diǎn)時(shí)，則結(jié)論為

BD·DC=d2-r2．

這就是切割線(xiàn)定理，兩者可以統(tǒng)一寫(xiě)作

BD·DC=|r2-d2|,

其中點(diǎn)D為線(xiàn)段BC的一個(gè)分點(diǎn)．

例2如圖14，在等腰Rt△ABC中，AB=AC，∠BAC=90°，求證：BD2+DC2=2AD2．

本題證明方法很多，這里利用命題2給出證明．

證明把等腰Rt△ABC補(bǔ)成為一個(gè)正方形ABEC，則AD=ED，根據(jù)命題2，有

DA2+DE2=BD2+DC2,

從而

BD2+DC2=2AD2．

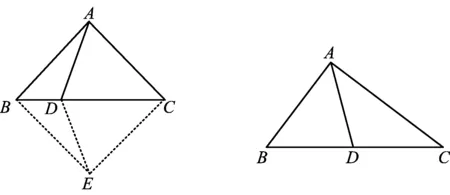
圖14 圖15

例3(三角形中線(xiàn)公式的證明)在△ABC中，AD為BC邊上的中線(xiàn)，求證：

證明1)如圖15，當(dāng)∠BAC為直角時(shí)，

2)如圖16，當(dāng)∠BAC為銳角時(shí)，以BC為對(duì)角線(xiàn)構(gòu)造矩形BECF，則由原題的一般結(jié)論得

AB2+AC2=AE2+AF2=

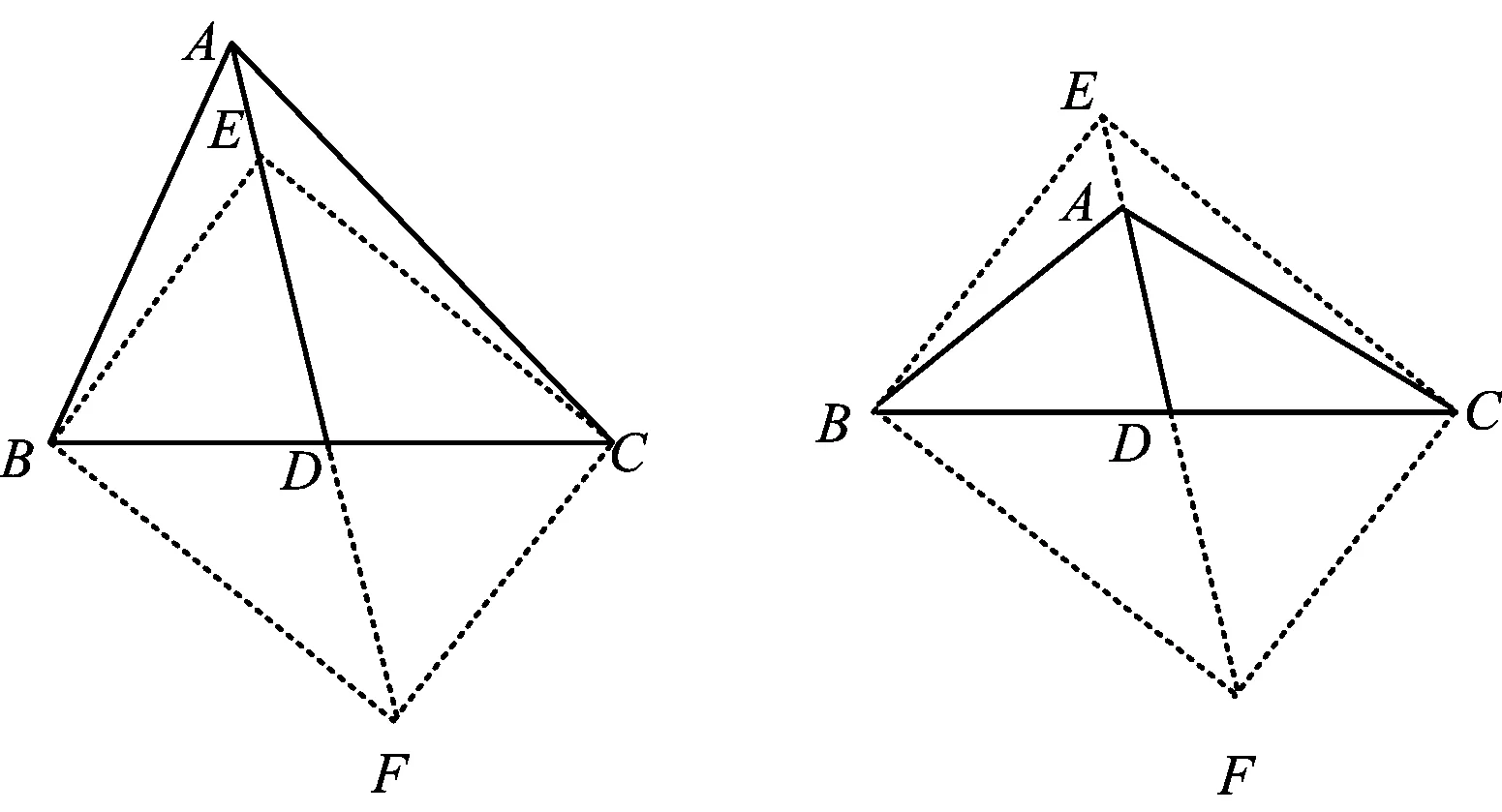
圖16 圖17

3)如圖17，當(dāng)∠BAC為鈍角時(shí)，以BC為對(duì)角線(xiàn)構(gòu)造矩形，由命題4得

AB2+AC2=AE2+AF2=

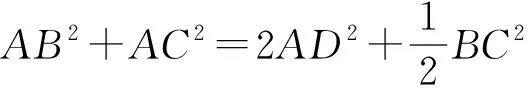
由此不難推導(dǎo)出三角形的中線(xiàn)長(zhǎng)公式