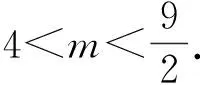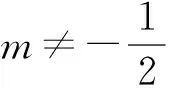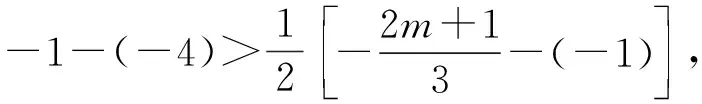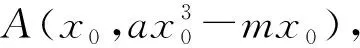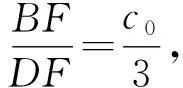不單調三次函數圖像中矩形性質的探究*

● ●

(正始中學,浙江 寧波 315131) (寧波市教育局教研室,浙江 寧波 315000)

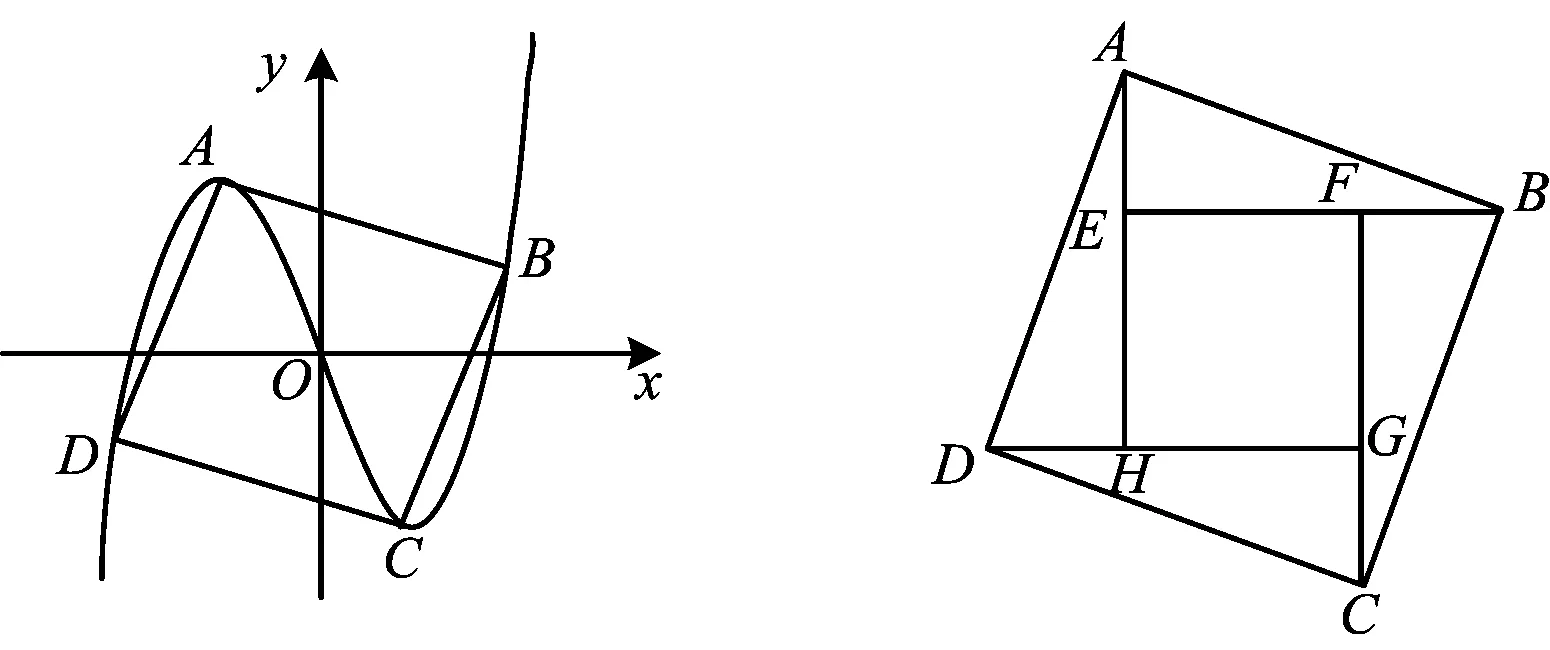
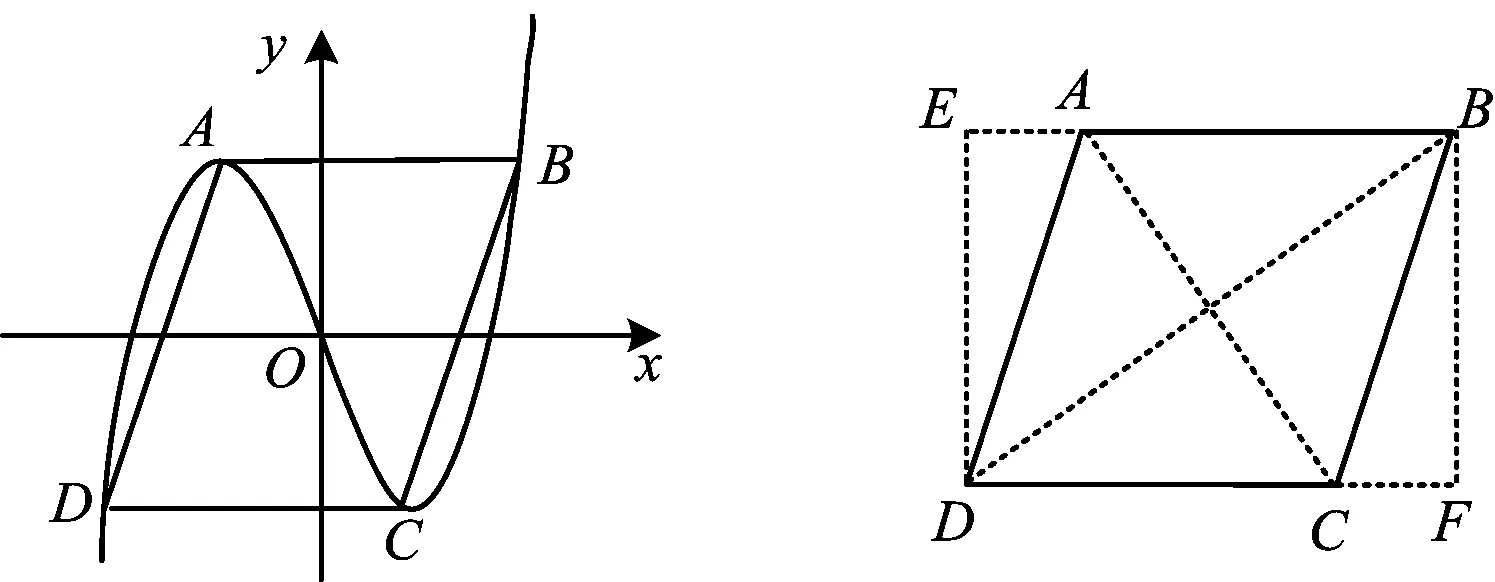
筆者在教學三次函數圖像與性質時，想到如下問題：不單調的三次函數分別以兩個極值點為切點作切線與三次函數圖像有兩個交點，以這兩個交點為對角線構成的矩形與三次函數圖像有什么關系?為了說明簡便，令三次函數f(x)=ax3+bx2+cx+d，由于對a>0與a<0的兩種情況研究方式類似，因此本文只研究a>0的情形．

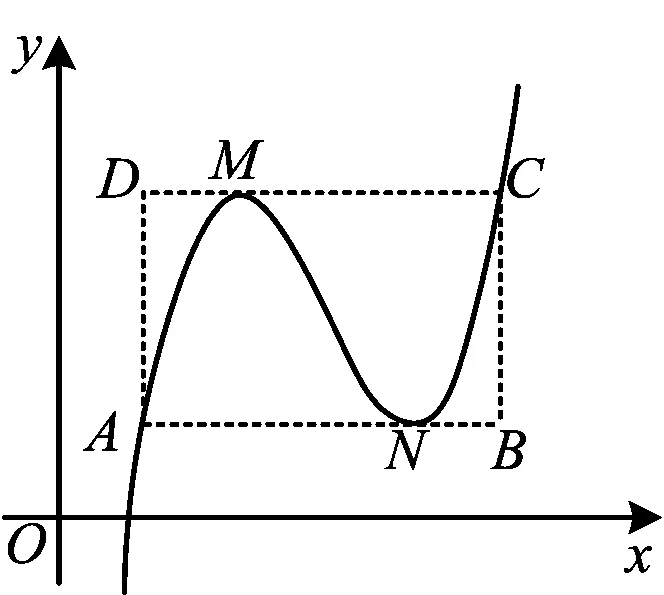
圖1

1 預備知識

1.1 定義矩形

當三次函數f(x)=ax3+bx2+cx+d(其中a>0)在R上不單調時，f′(x)=3ax2+2bx+c的判別式Δ=4(b2-3ac)>0，導函數有兩個不相等的零點x1,x2(其中x10)的矩形．

1.2 簡化形式

對三次函數f(x)=ax3+bx2+cx+d(其中a>0)進行配方，得

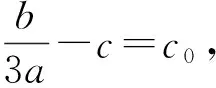
g(x)=ax3-c0x.

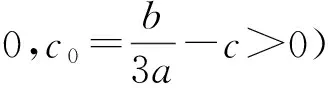
2 探究矩形的一些結論

定理1不單調的三次函數過兩個極值點分別作切線與三次函數圖像有兩個交點，以這兩個交點連接線段為對角線構成矩形，則兩個極值點分別是這個矩形邊上的四等分點．

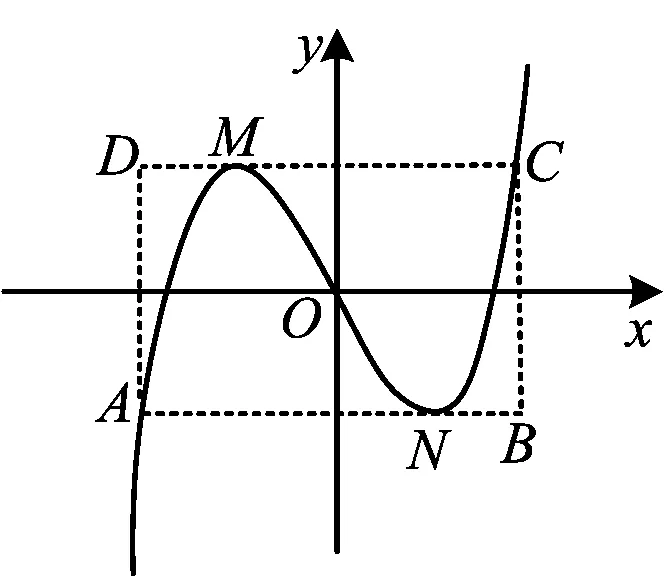
圖2

證明令三次函數g(x)=ax3-c0x(其中a>0,c0>0)．由

g′(x)= 3ax2-c0=

知

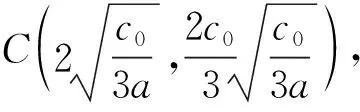
因為函數f(x)可由函數g(x)平移得到，所以兩個函數的矩形大小相同，且對應點之間的比例關

系不變，于是

1)在不單調三次函數f(x)=ax3+bx2+cx+d(其中a>0)中，由圖2知xA,xM,xO,xN,xC成等差數列，令等差數列的公差為H，根據定理1易得

2)設不單調三次函數的中心坐標為P(x0,f(x0))，則f(x0-d)=f(x0+2d)均等于極大值，f(x0+d)=f(x0-2d)均等于極小值．

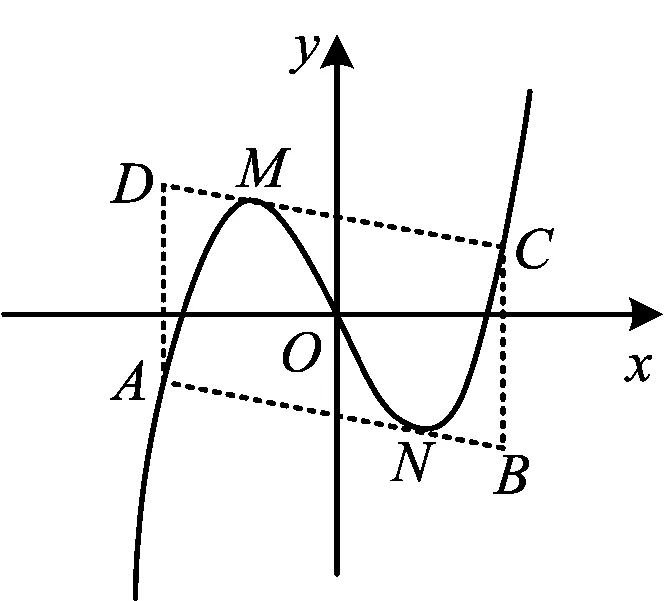
圖3

推論1已知不單調的三次函數g(x)=ax3-c0x，如圖3所示，過曲線上兩個點M,N分別作切線與三次函數圖像交于點A,C，且CM∥AN;過點A,C作豎線交切線于點B,D構成ABCD，則兩個切點M,N分別是這個平行四邊形邊上的四等分點．

證明函數g(x)=ax3-c0x(其中a>0,c0>0)的圖像如圖3所示，則

g′(x)=3ax2-c0.

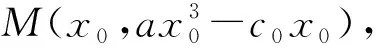
與g(x)=ax3-c0x聯立，得

解得x=x0或x=-2x0，即xC=-2x0.由對稱性可得xD=xA=2x0,易得M為DC的四等分點．又由對稱性可知N為AB的四等分點，故兩個切點M,N分別是這個平行四邊形邊上的四等分點．

推論2如果不單調的三次函數為g(x)=ax3-c0x，那么參數c0決定矩形的形狀(即水平的長與垂直的寬之比)．

矩形的水平邊長與垂直邊長之比為

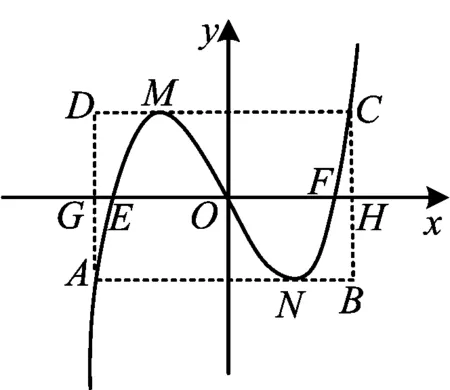
圖4

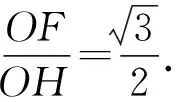
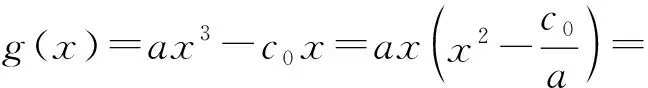
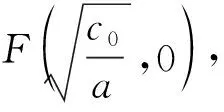
3 c0取特殊值時的幾個結論

1)當c0=3時，“一個矩形”是正方形；

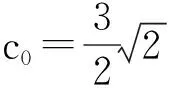
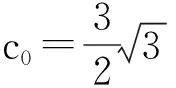
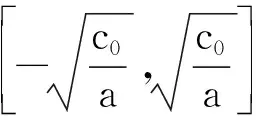
利用不單調的三次函數圖像中矩形的性質定理和推論不難證明以上結論，具體請讀者自行完成證明．

4 應用舉例

例1已知函數f(x)=x3+(m+2)x2+(2m+1)x(其中m∈R),設函數f(x)除0外還有兩個不同的零點x1，x2(其中x1x2≠0，且x1f(-4)恒成立，求實數m的取值范圍．

解由題意得

f(x)=x·[x2+(m+2)x+(2m+1)]，

可知x1,x2是方程x2+(m+2)x+(2m+1)=0的兩個不相等的非零根，于是

Δ=(m+2)2-4(2m+1)>0，

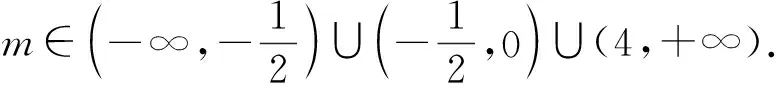
1)當m>4時，

從而

x1

綜上所述，實數m的取值范圍是

例2如圖5，已知函數f(x)=x3-mx，直線l1∥l2，l1與函數f(x)的圖像切于點A,交于點B;l2與函數f(x)的圖像切于點C,交于點D,若四邊形ABCD為正方形，求m的值．

圖5 圖6

即

例3設與x軸平行的兩條直線l1,l2與函數f(x)=x3+ax2+bx+c的圖像各恰有兩個公共點.證明：以這4個點為頂點的四邊形為菱形的充要條件是這個四邊形的面積為6.

(2015年保加利亞國際高中數學競賽試題)

圖7 圖8

證明平移函數圖像，使得AC的中點為原點(如圖7)，構成新的函數

構建三次函數矩形(如圖8)．

必要性：由推論2可得

又由三次不單調函數圖像中矩形的性質定理可得A為BE的四等分點，則

已知四邊形ABCD為菱形，從而

解得

即

解得

則

從而

充分性：已知S四邊形ABCD=6，則

即

解得

此時

即kBD·kAC=-1，故四邊形ABCD為菱形．

綜上所述，以這4個點為頂點的四邊形為菱形的充要條件是這個四邊形的面積為6．

從上面問題的發現、提出、分析和解決的過程之中能充分感受到數學的簡約美、嚴謹美、對稱美與和諧美[1]．

參考文獻

[1] 任偉芳.歷經三重境界探究橢圓性質的一個案例[J].中學教研(數學)，2013(10)：23-26．