對一節失敗的高三專題復習課的反思*

●

(廣州市第四中學,廣東 廣州 510170)

1 教學背景

不久前，筆者上了一節失敗的高三專題復習課．為什么說這節課是失敗的呢？這是怎樣的一節課呢？從選題，到備課，到上課，有哪些經驗教訓呢？針對這節課，筆者進行了反思，以供大家探討，希望對高三的復習備考有借鑒價值．

當時教學進程已進入了高考第二輪專題復習，在幾次周測中，筆者發現學生在遇到復合函數零點問題的選擇題時，正確率特別低.而復合函數零點問題又是一個熱門考點，在各地的模擬考中出現的頻率較高，因此，有必要教會學生復合函數零點問題的一般解題方法．

復合函數零點問題的一般解題方法是：換元法、圖像法．雖然這類題目綜合程度較高，解題方法步驟繁瑣，容易出錯，但是解題原理并不難，解題方法步驟也比較固定.筆者所任教班級是重點班，學生思維活躍，具備通過學習掌握這種方法的基礎．

復合函數零點問題，涉及到函數、方程、導數、極限、零點、不等式等知識點，蘊含了函數與方程、化歸與轉換、數形結合等數學思想，具有較高的教學價值．

基于上述原因，筆者確定了以“復合函數零點問題”作為公開課的主題．

2 設計思路

本節課是一節解題課，教學基本程序有3個階段：解題方法的習得、解題方法的轉化、解題方法的遷移與應用[1]．具體的教學環節如下：

環節1解題方法的習得.

1)嘗試做題、展示交流.

師生活動學生嘗試做例題．幾名學生展示自己的思路，師生進行交流．

設計說明讓學生思考，形成初步的解題思路，并進行展示交流，暴露問題，分析各種解題思路的可行性．

2)方法講解.

師生活動教師分析例題，講解解題方法與步驟．

設計說明教師講解的關鍵：揭示問題的本質，將原問題進行等價轉化；畫出函數圖像，數形結合，進行求解．

環節2解題方法的轉化——模仿例題、運用方法.

師生活動學生做練習，教師巡視，發現學生存在的問題，作針對性講解．

設計說明教師針對講解時，要注意兩個問題：1)題目的等價轉化；2)換元法、圖像法的細節．

環節3解題方法的遷移與應用.

1)變式訓練、形成技能.

師生活動學生做余下的練習，教師巡視，針對學生的做題情況進行講解．

設計說明通過變式練習，最終達到學生深刻理解解題原理、熟練運用方法、形成解題技能的目的．

2)方法總結.

師生活動教師總結復合函數零點問題的一般解題方法與步驟．

設計說明總結方法，點出此類題涉及到的數學思想．

3 學案選題

這節課筆者選取了6個題目：1個例題，5個練習題．打算先通過一個例題講解解題方法，再通過練習鞏固解題方法．為了方便說明問題，下面給出例題的詳解．

( )

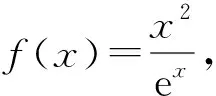
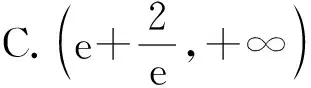
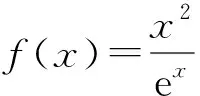
表1 f ′(x)和f(x)的取值情況

易知當x→-∞時，f(x)→+∞；當x→+∞時，f(x)→0+．

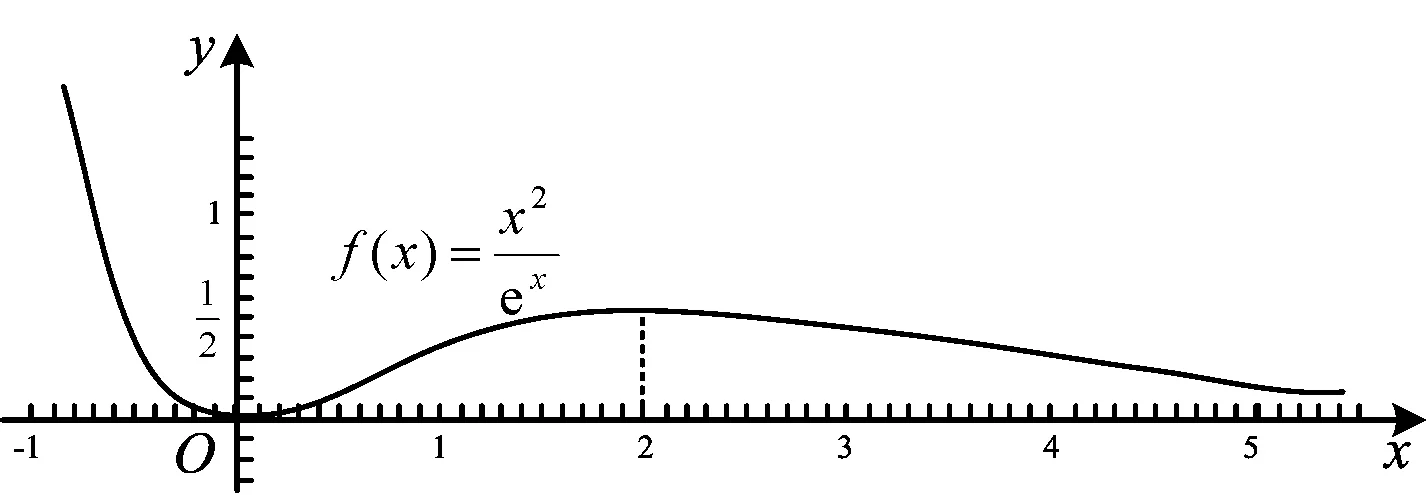
圖1

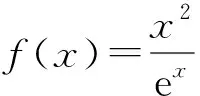
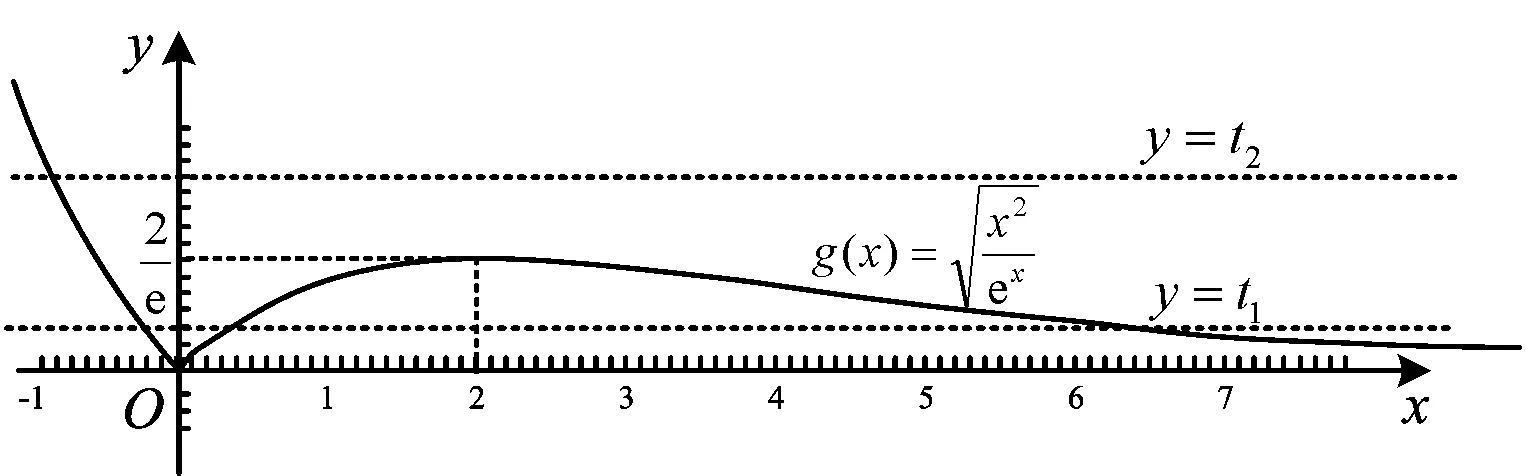
圖2

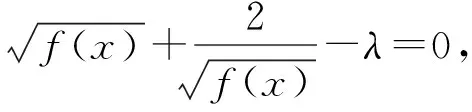
即

t2-λt+2=0．

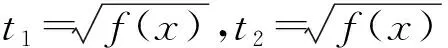
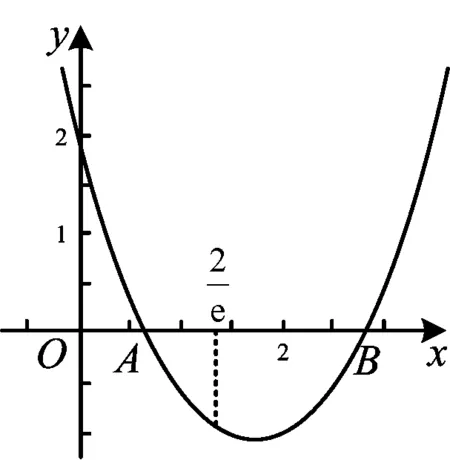
圖3

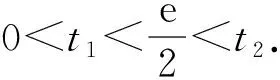
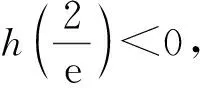
4 教學情況

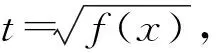
在展示交流環節，原來設想的激烈的思維碰撞場面并未出現．有思路的幾個學生頻頻發言，但解題方向不明，而余下的學生成了沉默的大多數．筆者首先針對學生現有的解題思路，進行分析點評，指出其錯誤或不當之處，這已經花費了好些時間，然后再對題目進行詳細分析、講解．

本題的解題思路分析如下：

第1步，換元，原問題等價于

有4個實根x1,x2,x3,x4．

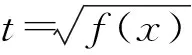
第3步，關于t的方程t2-λt+2=0可能有多少個根？(由圖2可知：可能有0,1,2個根.)

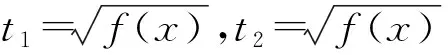
第5步，畫圖、列式、解決問題．

完成例題的講解后，筆者讓學生做練習，發現仍有相當多的學生不能將問題等價轉化而陷入困境．筆者只能逐題講解，整節課成了教師的獨角戲，學生思維參與度較低，原來設計的練習題也沒有做完，教學任務沒有完成．

5 教學反思

一節課的失敗是由多個因素造成的，本節課失敗的原因主要有以下兩個方面：

1)例題選取不當[2]．例題難度過大，前面缺少必要的容易題作鋪墊，學生入手困難．

②原問題的等價轉化，是學生難以理解和接受的．學生習慣于從字面上理解題目，考慮的是“方程的解”的問題，不能將題目轉化為“函數的零點”“兩個函數的交點”問題，缺乏數形結合思想．而且，本題要將原問題轉化為兩組函數的對應交點問題，這是本題最難的地方．

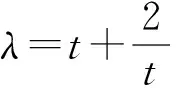
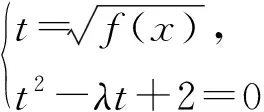
即

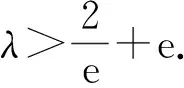
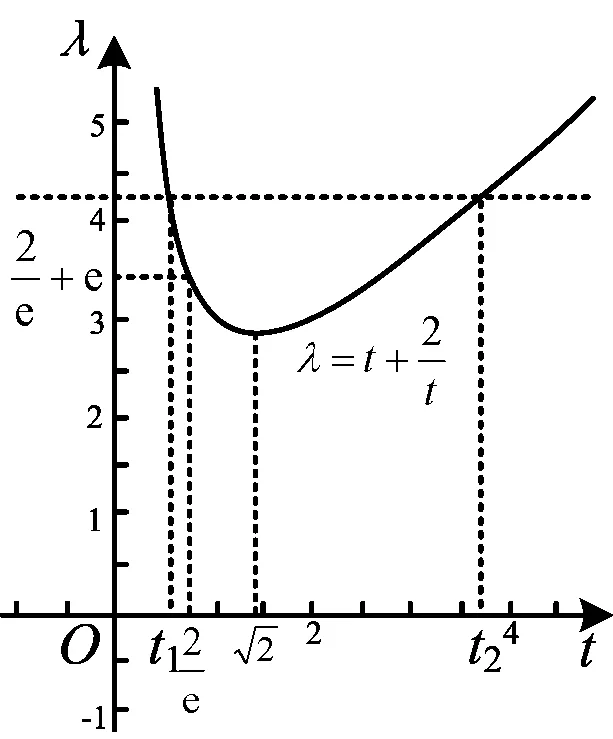
圖4

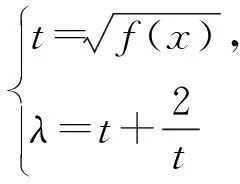
從上述解法可以看出，本題綜合程度較高，存在多種解法，且每一種解法都不容易理解．對于多數學生來說，幾種解題思路在頭腦中糾纏，學生陷入困境，不知所措．

2)對教學重點、難點理解不到位．講解例題時，側重于解題技巧，忽視了數學思想．

①本題涉及到較多的概念，應當進行概念的二次教學，提煉概念蘊含的數學思想[3]．例如，復合函數的相關概念與換元法，涉及到“函數(對應)思想”．筆者在講授時，缺乏對復合函數必要的復習回顧，也沒有提煉其中蘊含的數學思想．

②復合函數零點問題，本質上是在考查數形結合思想．方程的根、函數的零點、兩個函數的交點，這三者之間的對應關系需要進行梳理．筆者在講授時，未明確指出這三者之間的對應關系，對數形結合思想強調不夠．

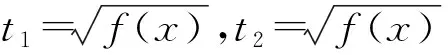
6 改進后的教學設計

根據上述反思剖析，筆者將教學設計進行了改進，改進后的教學設計如下：

6.1 復習引入

1)什么叫復合函數？

2)f(x)=e2x-2ex-3可以看成哪幾個函數復合而成？

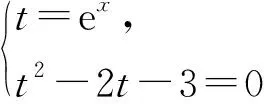
設計說明復習復合函數的有關概念，幫助學生回憶解題要用到的有關知識．在點評引入3)時，注意兩點：第一，要強調“對應”：t2-2t-3=0有兩個解t1=3，t2=-1,一個t對應一個x，另一個t找不到對應的x(即ex1=3有解x1=ln 3，ex2=-1無解)．第二，要有意識地用圖像來進行說明，強調方程的根、函數的零點、兩個函數的交點這三者之間的對應關系，強調“數形結合”(如圖5和圖6).

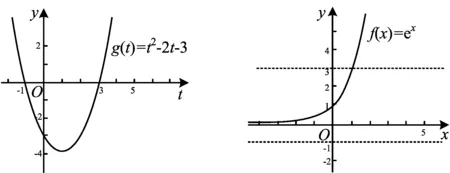
圖5 圖6

6.2 例題講解

例2關于x的方程t=-x3+3x+2恰有3個根，求實數t的取值范圍．

例3關于x的方程t=|-x3+3x+2|恰有4個根，求實數t的取值范圍．

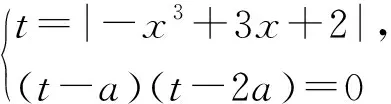
例5同例1.

設計說明1)在例5的前面設置3個例題，每個例題有各自的目的：例2是學生熟悉的三次函數，圖像簡單，題型常規，起點低，入手快；例3在三次函數的基礎上，加一個絕對值，繼續強化數形結合思想，承上啟下；例4需要畫兩組函數的圖像，分析交點情況，為例5的解決作準備．這樣，4個例題層層深入，難度遞進，前一題為后一題作鋪墊，容易激發學生的學習積極性．

2)例5(原例1)的講解，可以進一步優化如下：

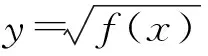
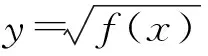
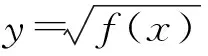
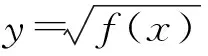
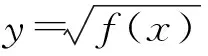
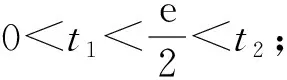
⑧如圖3，由零點定理有

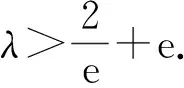
6.3 課堂練習

( )

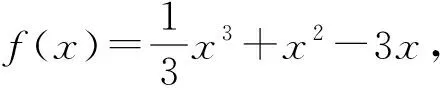
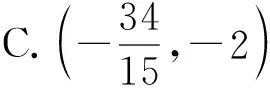
答案：C.

2)已知函數f(x)=|x·ex|，g(x)=f2(x)+λf(x)，若方程g(x)=-1有且僅有4個不同的實數解，則實數λ的取值范圍是______．

( )

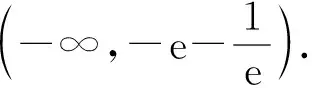
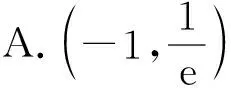
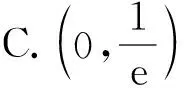
答案:C.

( )

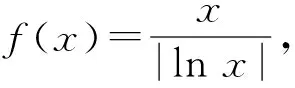
答案:C.

5)已知函數f(x)=|sinx|(其中x∈[-π,π])，g(x)=x-2sinx(其中x∈[-π,π])，設方程f(f(x))=0，f(g(x))=0，g(g(x))=0的實根的個數為分別為m,n,t，則m+n+t=

( )

A．9 B．13 C．17 D．21

答案:B.

專題復習，不是隨隨便便選幾個題組合在一起就構成一個復習專題，而要進行精心設計，內容不能過難或過易，要有梯度，層層遞進．專題復習的講解，不是就題論題，不是講解題技巧，而要側重于滲透數學思想方法．波利亞曾說過，完善的思想方法猶如北極星，許多人通過它而找到正確的道路．數學思想方法是解題的指導思想和基本策略，在教學中要注意滲透數學思想方法，這對于學生在學習過程中理解數學本質、激發學習興趣、發展創造能力大有裨益．

參考文獻

[1] 譚國華．高中數學解題課型及其教學設計[J]．中學數學研究，2013(8)：12-16.

[2] 金明，吳潤文．讓探究成為高三微專題復習課的主旋律——以一節高三專題復習課為例[J]．中學數學:高中版，2017(5)：5-8.

[3] 吳新建．高三微專題復習課的實踐與思考——以復合函數的零點問題的教學為例[J]．數學通報，2016(5)：43-45.