Heisenberg李(超)代數的自同構群

劉 蕾,唐黎明

(哈爾濱師范大學數學科學學院,黑龍江哈爾濱 150025)

1 引言

近年來,Heisenberg李(超)代數的結構和表示一直是非常重要的研究課題,許多學者對此有著廣泛研究.例如,文[1]研究了特征0代數閉域上2m+n+1維Heisenberg李超代數的表示;文[2]研究了復數域上無限維Heisenberg代數的全形和全形的導子代數,證明了其全形的導子代數是一個完備李代數;文[3]研究了特征2域上2n+1維Heisenberg李代數的同調;文[4]研究了向量超空間上有限維Heisenberg李超代數不變的超對稱和超正交雙線性型;文[5]研究了特征0代數閉域上兩種類型Heisenberg李超代數的極小忠實表示.

本文約定在交換環上討論Heisenberg李代數的自同構群,在特征0代數閉域上討論Heisenberg李超代數的自同構群.仿照文[6]中交換環上嚴格上三角矩陣李代數的自同構和文[7]中復向量空間上Heisenberg李代數的自同構的刻畫,參照文[3,7]中Heisenberg李代數的定義,利用文[7]中Heisenberg李代數與線性李代數之間的同構,本文研究了交換環上Heisenberg李代數的自同構,包括內自同構、中心自同構、對合自同構,進而得到其自同構群的子群,包括內自同構群、中心自同構群、對合自同構群.利用文[5]中有限維Heisenberg李超代數的定義,本文建立了Heisenberg李超代數與線性李超代數之間的同構,從而研究了特征0代數閉域上Heisenberg李超代數的自同構,包括內自同構、中心自同構、對合自同構,進而得到其自同構群的子群,包括內自同構群、中心自同構群、對合自同構群.

2 基本概念和引理

令R是具有單位元的交換環并且Mn(R)是R上所有n×n矩陣構成的集合,其中n是正整數.令eij表示第i行第j列元素為1,而其余元素為0的矩陣,其中i,j是正整數.

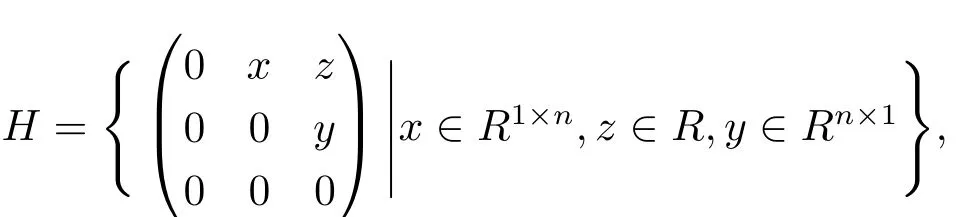
作成一個李代數,稱H為Heisenberg李代數.

令F是特征0代數閉域并且Mn(F)是F上所有n×n矩陣構成的集合,其中n是正整數.

定義2.2[5]F上具有一維中心的二步冪零李超代數稱為Heisenberg李超代數,并且Heisenberg李超代數分為以下兩種類型.

(1)令是具有偶中心的Heisenberg李超代數,設

為它的一個基,并且李超運算由以下給出[ui,vi]= ?[vi,ui]=z=[wj,wj],?i=1,···,m,j=1,···,n,其余基元素之間的李超運算均為0.

(2)令是具有奇中心的Heisenberg李超代數,設

為它的一個基,并且李超運算由以下給出[vi,wi]=z=?[wi,vi],?i=1,···,n,其余基元素之間的李超運算均為0.

根據定義2.2證得以下兩個引理.

引理2.3令是一個線性李超代數,其中

設線性映射f

其中

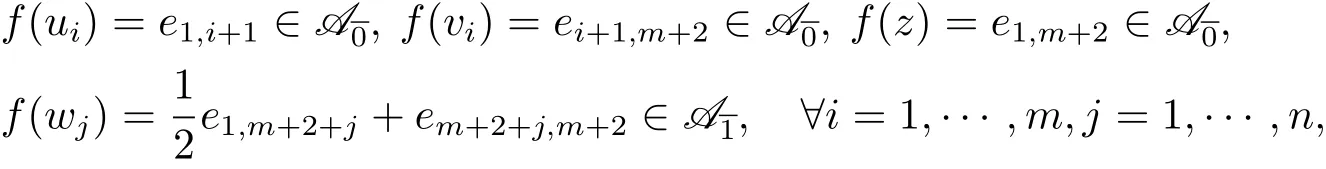
則f是一個李超代數同構.

引理2.4令F上是一個線性李超代數,其中

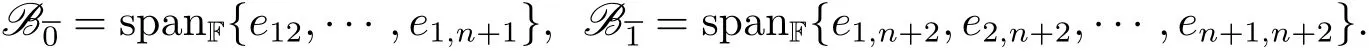
設線性映射g

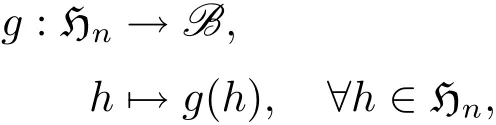
其中,則g 是一個李超代數同構.

3 主要結果及證明

記Aut(H)為Heisenberg李代數H的自同構群.

定理3.1設d∈Mn+2(R)為可逆的對角矩陣,x∈H.令α=d+x,則α可逆.設映射

其中 σα(h)=αhα?1,則σα是H 的一個自同構,稱為H 的內自同構.令G是H 的所有內自同構構成的集合,則G是Aut(H)的子群,稱為H 的內自同構群.

證易知σα是雙射且是線性變換.由已知得α?1α=e,其中e是單位矩陣.?h1,h2∈H,可得

因此 σα([h1,h2])=[σα(h1),σα(h2)].故 σα是 H 的一個自同構.?σα,σβ∈ G,h ∈ H,可得

因此 σασβ=σαβ∈G.?σα∈G,h∈H,可得

因此故G是Aut(H)的子群.

定理3.2令F={f∈HomR(H,R)|f(y)=0,?y∈ δ[1](H)},其中 δ[1](H)=[H,H].?f∈F,設映射

其中 ψf(h)=h+f(h)e1,n+2,則ψf是H 的一個自同構,稱為H 的中心自同構.令S是H的所有中心自同構構成的集合,則S是Aut(H)的子群,稱為H的中心自同構群.

證易知ψf是雙射且是線性變換.?h1,h2∈H,可得

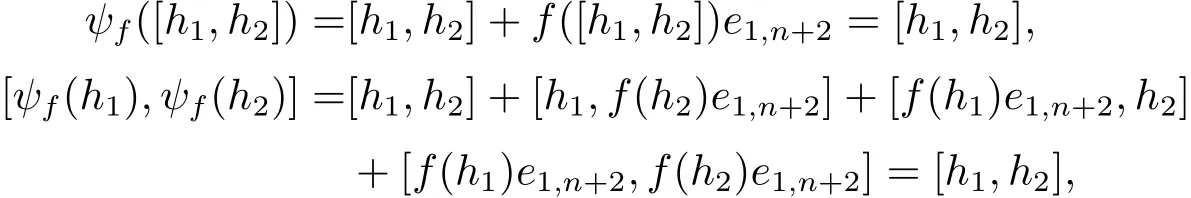
因此 ψf([h1,h2])=[ψf(h1),ψf(h2)],故 ψf是H 的一個自同構.?ψf,ψg∈ S,h∈ H,可得

因此 ψfψg= ψf+g∈ S.?ψf∈ S,h∈ H,可得 ψfψ?f(h)=(h?f(h)e1,n+2)+f(h)e1,n+2=h,因此 ψ?f=ψ?1f∈S.故S是Aut(H)的子群.

定理3.3令γ=e1,n+2+e2,n+1+···+en+2,1.設映射

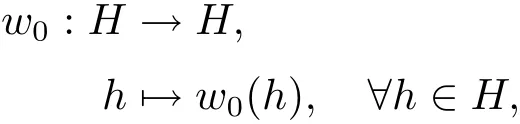
其中 w0(h)=?γhTγ,則w0是H 的一個自同構,稱為H 的對合自同構.令W={ι,w0},其中ι是恒等變換,則W 是Aut(H)的子群,稱為H 的對合自同構群.

證易知w0是雙射且是線性變換.由已知得γ2=e,γT= γ,其中e是單位矩陣.?h1,h2∈ H,可得

因此 w0([h1,h2])=[w0(h1),w0(h2)].故w0是H 的一個自同構.?w0∈W,h∈H,可得w0w0(h)= ?γ(?γhTγ)Tγ=h,因此 w20=ι∈W.故W 是Aut(H)的子群.

記Aut(?m,n),Aut(?n)分別為Heisenberg李超代數?m,n,?n的自同構群.

令α=d+x,則α可逆.設映射

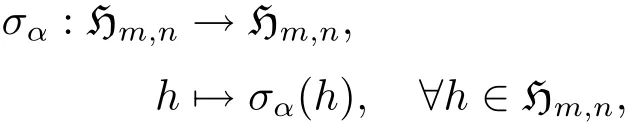
其中 σα(h)=αhα?1,則σα是?m,n的一個自同構,稱為?m,n的內自同構.令G1是?m,n所有內自同構構成的集合,則G1是Aut(?m,n)的子群,稱為?m,n的內自同構群.

證易知σα是雙射且是線性變換.由已知設

則有

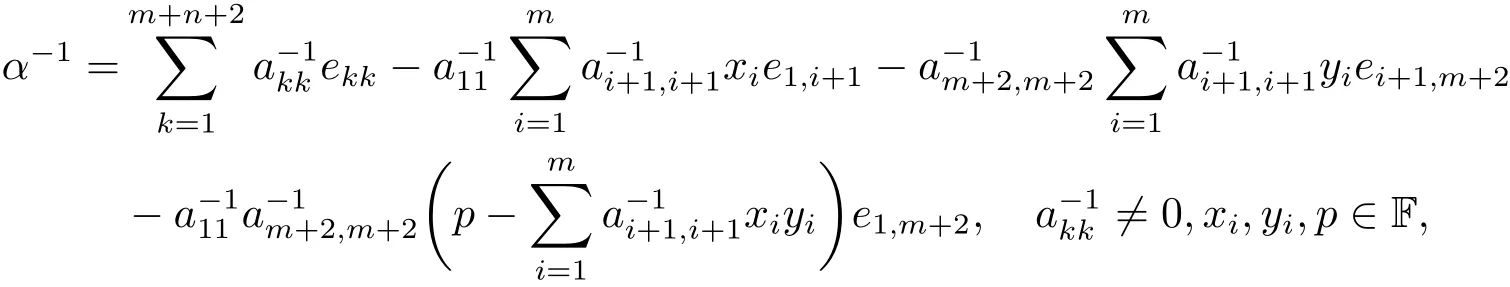
其中由引理2.3,設

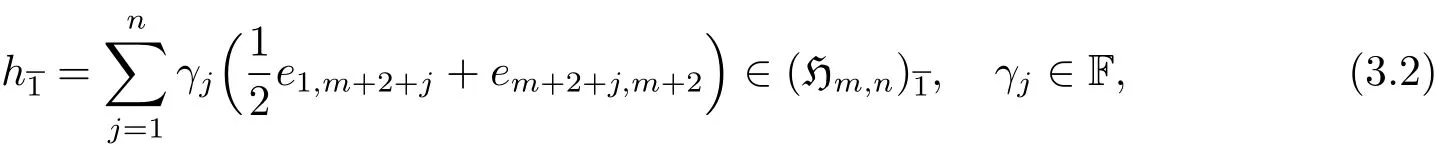
則有

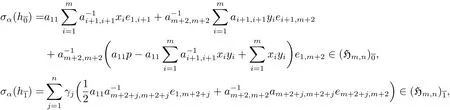
故σα是偶的線性變換.由引理2.3,設

則有

因此 σα([h1,h2])=[σα(h1),σα(h2)].故σα是?m,n的一個自同構.由定理3.1的類似證明可得G1是Aut(?m,n)的子群.

定理 3.5令 a=(a1,b1,···,am,bm)∈ F2m.設映射

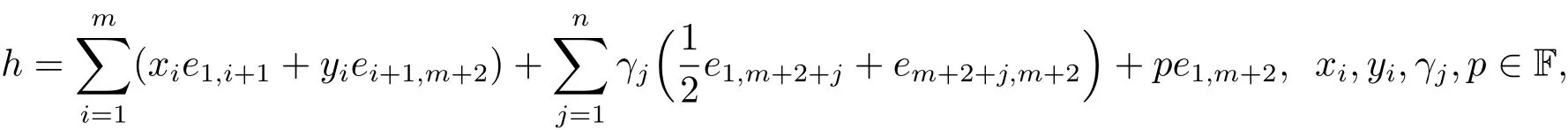
則ψf是?m,n的一個自同構,稱為?m,n的中心自同構.令S1是?m,n所有中心自同構構成的集合,則S1是Aut(?m,n)的子群,稱為?m,n的中心自同構群.

證易知ψa是雙射且是線性變換.由(3.1)和(3.2)式可得

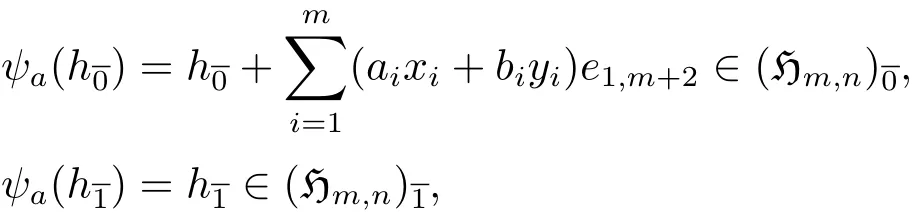
故ψa是偶的線性變換.由定義2.2和引理2.3可得 ψa(e1,m+2)=e1,m+2.?h1,h2∈?m,n,可得ψa([h1,h2])=[h1,h2],

因此 ψa([h1,h2])=[ψa(h1),ψa(h2)].故ψa是?m,n的一個自同構.由定理3.2的類似證明可得S1是Aut(?m,n)的子群.

其中 w0(h)=γhγ,則w0是?m,n的一個自同構,稱為?m,n的對合自同構.令W1={ι,w0},其中ι是恒等變換,則W1是Aut(?m,n)的子群,稱為?m,n的對合自同構群.

證事實上w0∈G1,{ι,w0}構成G1的子群.

定理3.7設d∈Mn+2(F)為可逆的對角矩陣,x∈(?n)0.令α=d+x,則α可逆.設映射

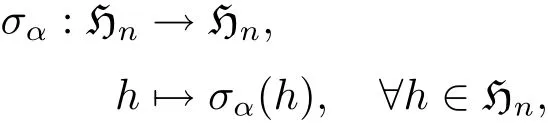
其中 σα(h)=αhα?1,則σα是?n的一個自同構,稱為?n的內自同構.令G2是?n所有內自同構構成的集合,則G2是Aut(?n)的子群,稱為?n的內自同構群.

證易知σα是雙射且是線性變換.由已知設

則有

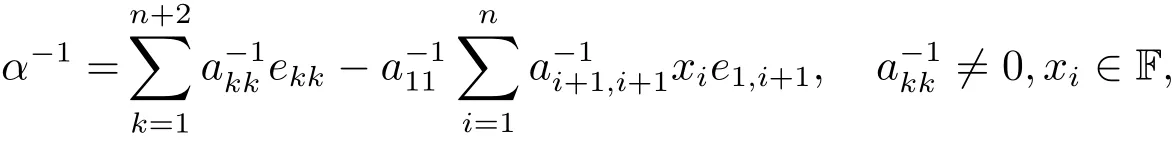
其中由引理2.4設

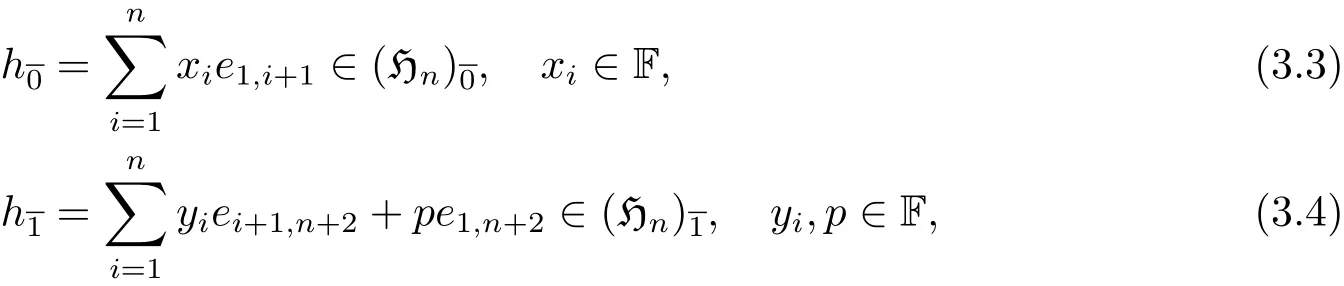
則有

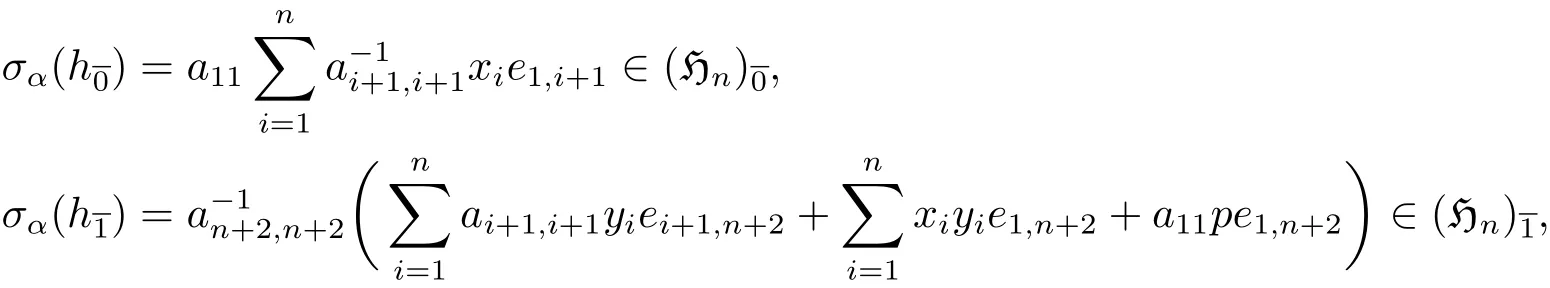
故σα是偶的線性變換.由引理2.4設

則有

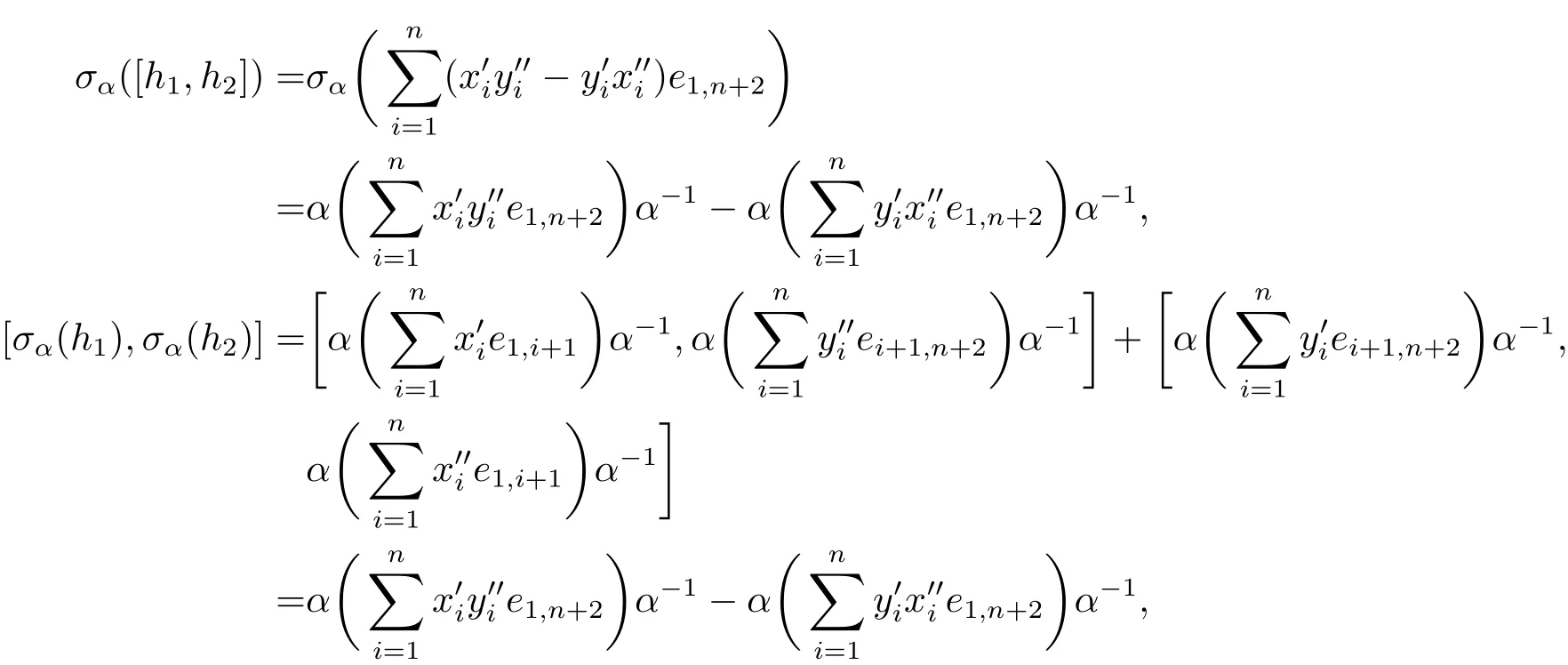
因此 σα([h1,h2])=[σα(h1),σα(h2)].故σα是?n的一個自同構.由定理3.1的類似證明可得G2是Aut(?n)的子群.

定理 3.8令 b=(b1,···,bn)∈ Fn.設映射

則ψb是?n的一個自同構,稱為?n的中心自同構.令S2是?n所有中心自同構構成的集合,則S2是Aut(?n)的子群,稱為?n的中心自同構群.

證易知ψb是雙射且是線性變換.由(3.3)和(3.4)式可得

故ψb是偶的線性變換.由定義2.2和引理2.4可得 ψb(e1,n+2)=e1,n+2.?h1,h2∈?n,可得

因此 ψb([h1,h2])=[ψb(h1),ψb(h2)].故ψb是?n的一個自同構.由定理3.2的類似證明可得S2是Aut(?n)的子群.

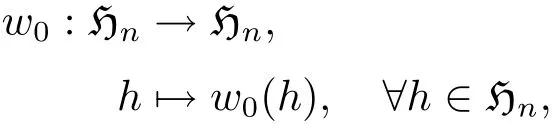
其中 w0(h)=γhγ,則w0是?n的一個自同構,稱為?n的對合自同構.令W2={ι,w0},其中ι是恒等變換,則W2是Aut(?n)的子群,稱為?n的對合自同構群.

證易知w0是雙射且是線性變換.由(3.3)和(3.4)式可得

故w0是偶的線性變換.由已知得γ2=e,其中e是單位矩陣.由(3.5)和(3.6)式可得

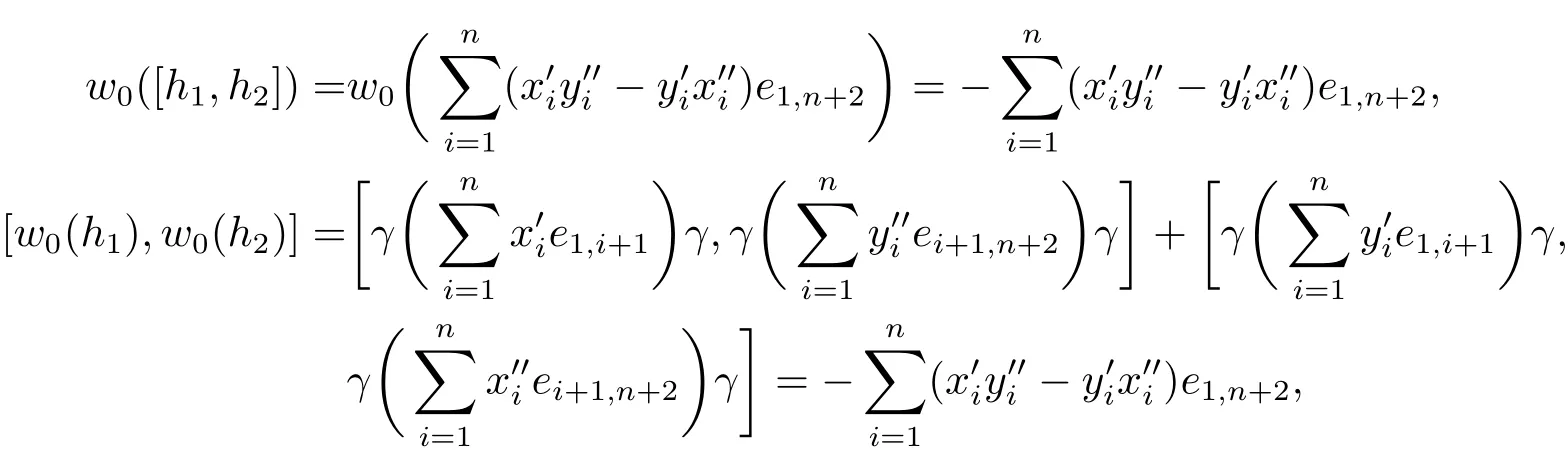
因此 w0([h1,h2])=[w0(h1),w0(h2)].故w0是?n的一個自同構.由定理3.3的類似證明可得W2是Aut(?n)的子群.

參考文獻

[1]Hegazi A S.Representations of Heisenberg Lie superalgebras[J].Indian J.Pure Appl.Math.,1990,21(6):557–566.

[2]Jang Cuibo.The holomorph and derivation algebra of in finite dimensional Heisenberg algebra[J].J.Math.,1997,17(3):422–426.

[3]Sk?ldberg E.The homology of Heisenberg Lie algebras over fields of characteristic two[J].Math.Proc.R.Ir.Acad.,2005,150(2):47–49.

[4]Rodr′?guez-Vallarte M C,Salgado G,S′anchez-Valenzuela O A.Heisenberg Lie superalgebras and their invariant superorthogonal and supersymplectic forms[J].J.Alg.,2011,332(1):71–86.

[5]Liu Wende,Chen Meiwei.The minimal dimensions of faithful representations for Heisenberg Lie superalgebras[J].J.Geom.Phys.,2015,89:17–24.

[6]Cao Youan,Tan Zuowen.Automorphisms of the Lie algebra of strictly upper triangular matrices over a commutative ring[J].Linear Alg.Appl.,2003,360:105–122.

[7]張海山,邵文武,盧才輝.Heisenberg李代數的自同構群[J].首都師范大學學報(自然科學版),2007,28(1):1–14.