分數(shù)布朗隨機流

肖艷萍,郭精軍

(1.西北民族大學(xué)數(shù)學(xué)與計算機科學(xué)學(xué)院,甘肅蘭州 730000)

(2.蘭州財經(jīng)大學(xué)統(tǒng)計學(xué)院,甘肅蘭州 730020)

1 引言

近些年,分數(shù)布朗運動因具有自相似性、長相依性等特點被廣泛地應(yīng)用于金融、通信等領(lǐng)域,已成為隨機分析及其相關(guān)領(lǐng)域研究的熱點問題之一.但是,當(dāng)Hurst參數(shù)時,分數(shù)布朗運動既不是半鞅,也不是馬爾科夫過程.于是,隨機分析中一些經(jīng)典的方法就不能直接拿來處理分數(shù)布朗運動相關(guān)問題了.

流概念源于幾何測度理論.最簡單的形式為如下泛函

基于文獻[6,8],本文利用白噪聲分析方法研究Wick積分意義下的分數(shù)布朗隨機流.行文安排如下:在第2部分中主要介紹分數(shù)布朗運動和白噪聲分析框架的一些基本事實;在第3部分,先給出Wick型分數(shù)布朗隨機流的定義,其次借助于解析刻畫定理證明分數(shù)布朗隨機流在白噪聲分析框架下是一個廣義泛函.

2 預(yù)備知識

該部分主要介紹分數(shù)布朗運動、白噪聲分析框架及一些相關(guān)結(jié)果,詳細內(nèi)容見文獻[2,7–8].

定義2.1[1?2]如果{BH(t)}t∈R是一個中心高斯過程且有

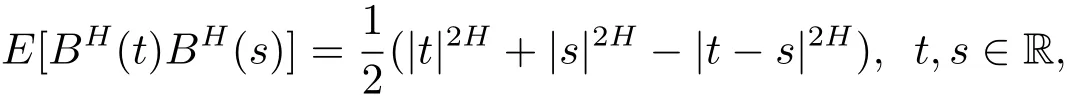
稱隨機過程{BH(t)}t∈R為分數(shù)布朗運動.

為了獲得BH(t)的表示形式,需要利用分數(shù)積分算子和微分算子,α∈(0,1).如果定義

如果定義

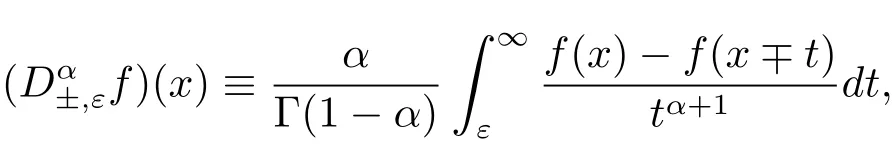
定義2.2[1?2]假設(shè)0＜H＜1,算子MH±定義為

則分數(shù)布朗運動有連續(xù)版本

第一組Gelfand三元組為S(R)? L2(R,Rd)? S?(R),其中S(R)和S?(R)分別為Schwartz向量值檢驗泛函空間和緩增函數(shù)空間.

設(shè)(L2)≡L2(S?(R),dμ)為S?(R)上關(guān)于μ平方可積泛函所構(gòu)成的希爾伯特空間.則由Wiener-It?-Segal同構(gòu)定理知,對每個f∈(L2)有以下混沌表示

設(shè)Γ(A)是A的二次量子化算子,其中A定義如下

對每個整數(shù)關(guān)于希爾伯特范數(shù)完備化空間.從而,設(shè)分別為的投影極限和歸納極限.于是,第二組Gelfand三元組為(S)?(L2)?(S)?.(S)(相應(yīng)地,(S)?)中元素稱之為Hida檢驗泛函(相應(yīng)地,廣義泛函).

對所有的檢驗泛函f∈S(R,Rd),在(S)×(S)?上定義S-變換如下

引理2.3[7?9]設(shè){Gk}k∈N表示U-泛函序列:

(1)對f∈S(R),{Gk(f)}k∈N是一個柯西列;

(2)存在Ci和p使得在R中一致有則存在唯一Φ∈(S)?使得S?1Gk強收斂于Φ.

引理2.4[7?9]設(shè)(?,B,μ)是一個可測空間以及在?上定義取值于(S)?的一個映射為Φλ.假設(shè)Φλ的S-變換滿足

(1)對所有的f∈S(R,Rd),是關(guān)于λ的μ-可測函數(shù);

(2)服從 U-泛函估計對固定的 p和對C1∈ L1(μ),C2∈ L∞(μ)成立,

從而Φλ在希爾伯特空間(S)?q中當(dāng)q足夠大時是Bochner可積的,

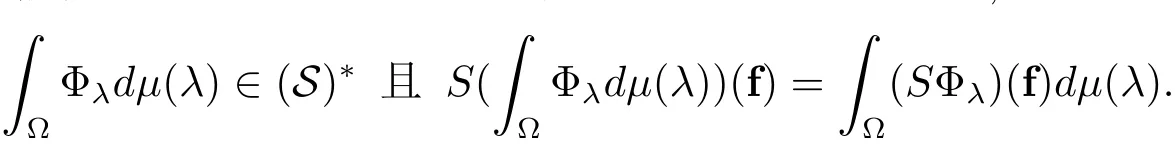
3 分數(shù)布朗隨機流

因為存在非適應(yīng)性積分,在定義分數(shù)布朗隨機流時,需要考慮隨機積分的處理難易性以及如何給出合理的解釋.在該部分中,首先給出Wick積分意義下的分數(shù)布朗隨機流的定義;其次討論該隨機流的存在性問題.

定義3.1設(shè)?:Rd→Rd定義在由所有光滑緊支撐向量域構(gòu)成的集合上,則

在倡導(dǎo)可持續(xù)發(fā)展的觀念之下，綠色建筑從建筑業(yè)中脫穎而出。相比于傳統(tǒng)建筑物而言，綠色建筑不僅可以節(jié)約水、煤氣、木材等自然資源，減少環(huán)境污染，而且也可以營造親近自然、舒適健康的居住氛圍，使居民身心得到舒展。

是一個泛函.Wick型分數(shù)布朗隨機流定義為

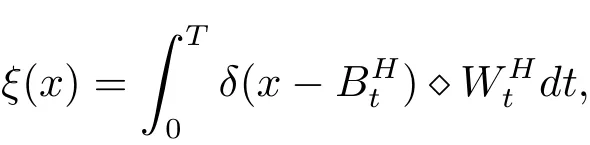
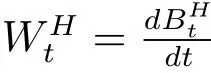
利用定義3.1可以證明:分數(shù)布朗隨機流在白噪聲分析框架下是一個Hida廣義泛函.

定理3.2對每個正整數(shù)d,每個H∈(0,1)和ε＞0,分數(shù)布朗隨機流

證對任意f∈S(R),首先驗證引理2.4中可積性條件滿足.計算S-變換

由文獻[1]中的引理2.5,定理2.3以及推論2.8,對f∈S(R),有

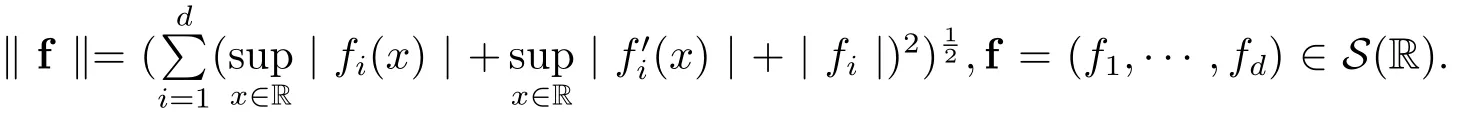
定理3.3對每個H∈(0,1)和d≥1,Bochner積分

和

都是Hida廣義泛函.進一步,當(dāng)ε趨于0時,ξH,ε(x)在(S)?中收斂到ξH(x).

則對所有的z∈C,有

最后一個等式在Rd上關(guān)于λ可積,同時第二部分關(guān)于λ是一個常數(shù).

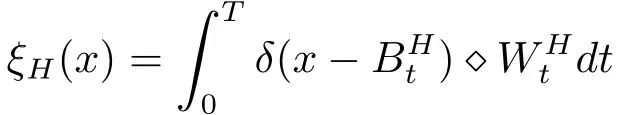
由控制收斂定理知,當(dāng)ε趨于0時,S(ξH,ε(x))(f)收斂于S(ξH(x))(f).由引理2.3知,當(dāng)ε趨于 0 時,ξH,ε(x) 收斂到 ξH(x).

文獻[6]利用Malliavin計算討論了Skorohod積分意義下的布朗和分數(shù)布朗隨機流.相比較Malliavin計算白噪聲分析方法在某種程度上將更方便,因為此時可以利用白噪聲分析方法方便地處理隨機積分問題.同時所獲得的結(jié)果對Hurst指數(shù)的要求更加寬泛,正則性條件也有別于文獻[6]中的條件:對時,分數(shù)布朗隨機流屬于Sobolev空間的條件是

參考文獻

[1]Bender C.An It? formula for generalized functionals of a fractional Brownian motion with arbitrary Hurst parameter[J].Stoc.Proc.Their Appl.,2003,104:81–106.

[2]Biagini F,Hu Y Z,?ksendal B,Zhang T S.Stochastic calculus for fractional Brownian motion and applications[M].London:Springer-Verlag,2008.

[3]Flandoli F.On a probabilistic description of small scale structures in 3D fluids[J].Ann.Inst.H.Poin.Prob.Stat.,2002,38:207–228.

[4]Flandoli F,Gubinelli M,Giaquinta M.Stochastic currents[J].Stoc.Proc.Their Appl.,2005,115:1583–1601.

[5]Flandoli F,Gubinelli M,Russo F.On the regularity of stochastic currents,fractional Brownian motion and applications to a turbulence model[J].Ann.Inst.H.Poin.Prob.Stat.,2009,45(2):545–576.

[6]Flandoli F,Tudor C A.Browinan and fractional Brownian stochastic currents via Malliavin calculus[J].J.Func.Anal.,2010,258:279–306.

[7]Obata N.White noise calculus and Fock space[M].Lect.Notes Math.,Berlin:Springer-Verlag,1994.

[8]Oliveira M,Silva J,Streit L.Intersection local times of independent fractional Brownian motions as generalized white noise functionals[J].Acta Appl.Math.,2011,113:17–39.

[9]Guo Jingjun,Li Chujin.On collision local time of two independent fractional Ornstein-Uhlenbeck processes[J].Acta Math.Sci.Ser.B,2017,37(2):316–328.

[10]Guo Jingjun,Jiang Guo,Xiao Yanping.Multiple intersection local time of fractional Brownian motion[J].J.Math.,2011,31(3):388–394.