自適應非張量積小波緊框架圖像去噪

黃素瑩,羿旭明

(武漢大學數學與統計學院,湖北武漢 430072)

1 引言

圖像去噪是進行圖像處理的前提,作為一項基礎性工作,許多學者對圖像去噪方法進行了大量的研究實驗.在眾多方法中,對圖像在頻域進行閾值量化的去噪效果得到學者們的廣泛認可[1?3,6].它的主要思路分為兩步,第一步是選用分解工具,將圖像分解至頻域,第二步是選取適當的閾值和閾值函數,在頻域對圖像進行閾值量化.其中,針對第一步,先后有學者提出了小波分解、小波包分解、最優小波包分解等方法,均能達到一定的去噪效果,但它們分解的方向性比較有限,使得去噪過程對圖像的細節和邊緣信息缺少保護,得到的去噪后圖像往往過于模糊.之后,Ron和Shen[4,5]提出了基于酉延拓定理(UEP)的非張量積小波緊框架分解思想,王等[6]在此基礎上構造了16個基于二元三次樣條函數的非張量積小波緊框架數字濾波器,其分解可以包含更多的方向信息,能較好地保護圖像的細節和邊緣,但他們在后半部分的閾值選擇上不盡理想,因此去噪效果還有提升空間.而針對閾值和閾值函數的選選取,研究文獻中先后提出了VisuShrink、NeighShrink和NormalShrink等自適應閾值算法[1,2]和相應的軟硬閾值函數,均能夠達到很好的去噪效果,在研究中被廣泛接受.

本文在文獻[6]的基礎上,構造了基于二元六次樣條函數的非張量積小波緊框架,基于香農熵采用最優分解層數自適應確定方法,并結合NormalShrink自適應閾值算法,在噪聲方差估計方法上做相應的改進,增強了算法的自適應性,由此形成本文的自適應非張量積小波緊框架圖像去噪算法.

2 非張量積小波緊框架的構造

UEP最早由Ron和Shen[4,5]提出,王等[6]進一步討論了其推廣和應用,并給出了如下定理.

定理2.1(UEP準則)設φ∈L2(R2)為一個具有緊支撐的細分函數,滿足

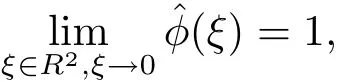
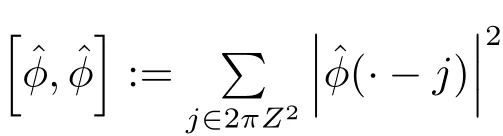
若{h1,h2,···,hr}是一組有限序列集合,其對應的傅立葉變換(ξ)(l=1,2,···,r)均可測和本性有界,且對任意的ν∈{0,π}2(0,0)和ξ∈[?π,π]2,滿足

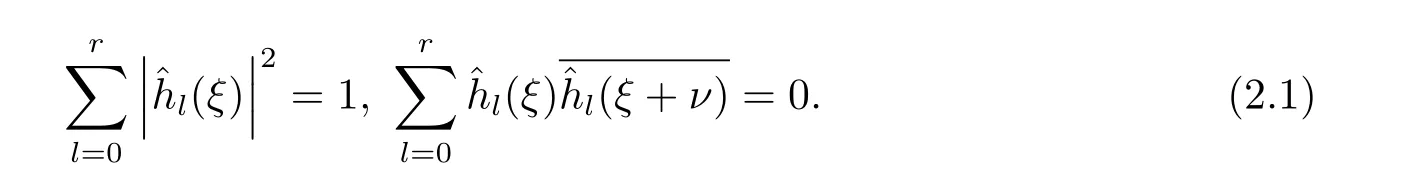
定義函數族則小波系

形成L2(R2)的一個小波緊框架.

滿足定理2.1的細分函數φ生成L2(R2)的多分辨分析

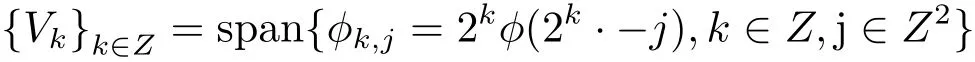
且對任意的f∈L2(R2),有

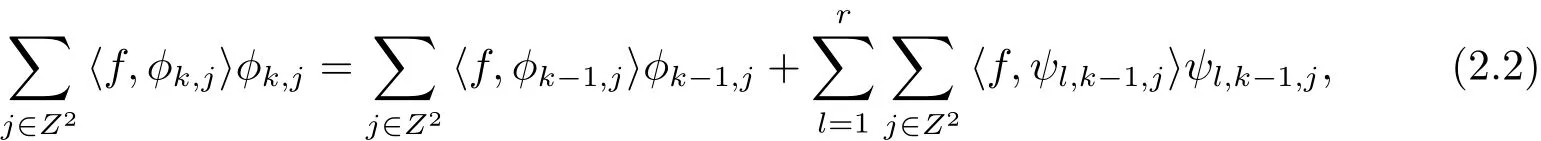
其中 {〈f,φk,j〉,〈f,ψl,k,j〉,l=1,2,···,r}k∈Z為框架系數.

記根據公式 (2.2) 可以導出如下基于小波緊框架的分解和重構公式[6]

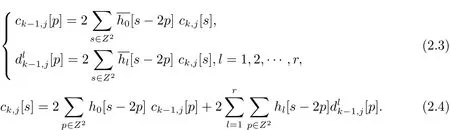
利用光滑余因子協調法[7?8],構造樣條空間中的二元六次樣條函數B(x,y),它的支集中心位于點且關于支集中心對稱,其傅立葉變換為

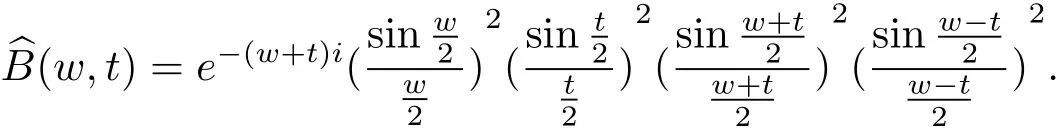
當取φ(x,y)=B(x,y)時,φ(x,y)滿足定理2.1的條件,其符號為

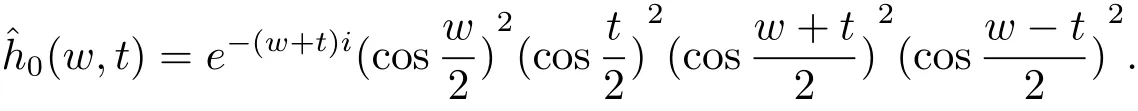
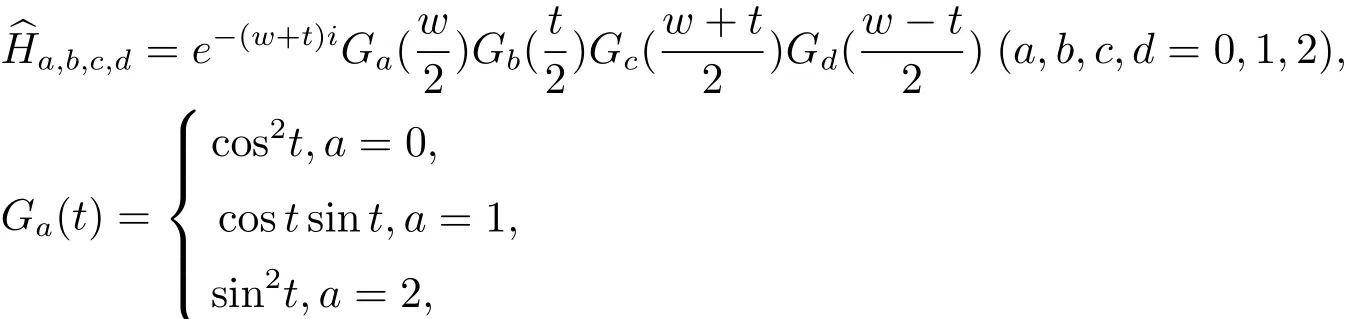
從而得到由a,b,c,d表示的81個符號為

進而得到對應的一組81個數字濾波器hl(l=0,1,···,80),如下所示

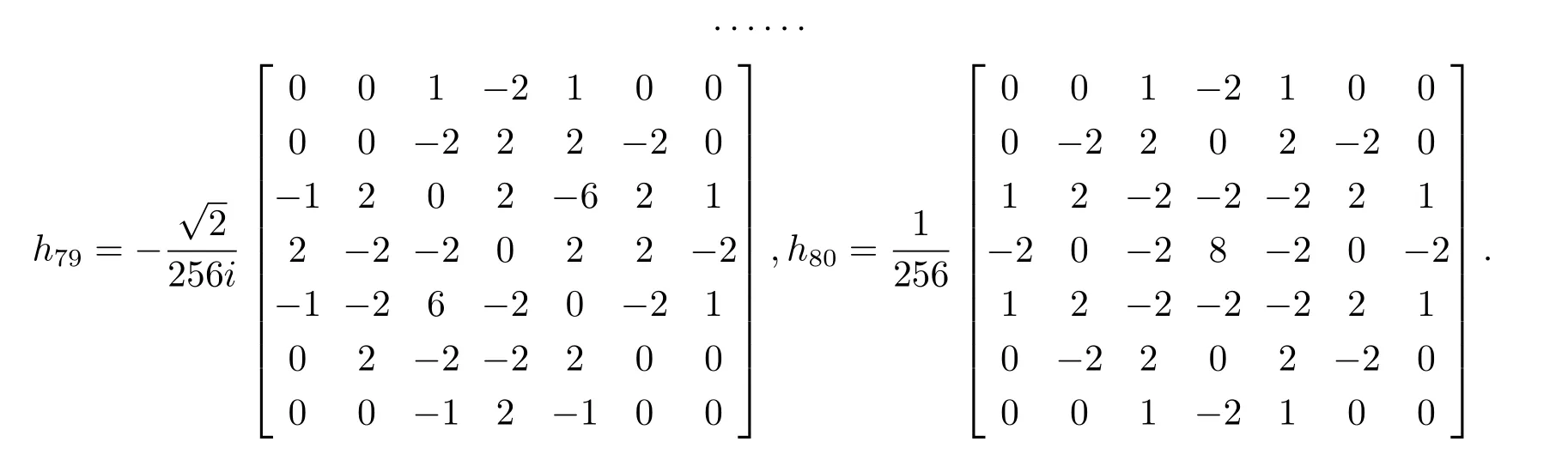
3 自適應非張量積小波緊框架圖像去噪算法

3.1 最優分解層數的自適應確定

文獻[6]推廣的基于二元三次樣條函數的非張量積小波緊框架分解,采用預先確定分解層數的方法,這樣導致去噪算法缺乏自適應性.本文在基于二元六次樣條函數的非張量積小波緊框架分解過程中,采用自適應確定最優分解層數的方法,通過計算每一次分解之后母帶與各子帶的“價值函數”,來確定是否保留此次分解.當母帶的“價值”大于各子帶的“價值”之和時,保留此次分解并繼續下一層分解,否則擯棄此次分解且分解過程結束.

對于“價值函數”的選擇,本文通過實驗比較,選用香農熵作為“價值函數”,其計算公式為

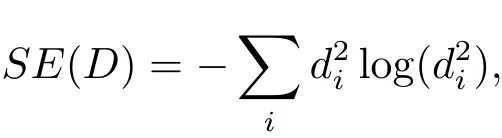
其中D是母帶或者各子帶對應的系數矩陣,di是矩陣元素.

3.2 自適應閾值的確定

本文基于去噪效果考慮,在NormalShrink自適應閾值算法上,針對噪聲方差σ2η的估計做了相應的改進,形成本文的自適應閾值算法.NormalShrink自適應閾值公式為

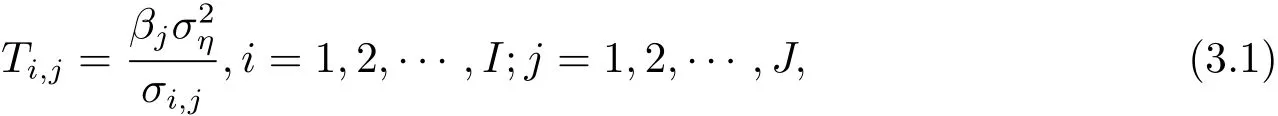
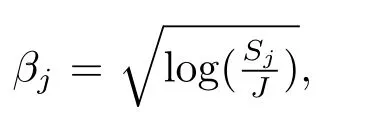
由于去噪后圖像系數和噪聲系數是相互獨立的,因此有其中是去噪后圖像中第j層第i個高頻子帶的方差.

圖像經過分解至頻域之后,噪聲信息大多保留在高頻子帶,而這些高頻子帶的方差可以看作是噪聲方差與去噪后圖像方差的相加.因此本文選取第1層分解之后的80個高頻子帶,分別計算其方差然后取其中最小值,并將其作為噪聲方差的估計,即

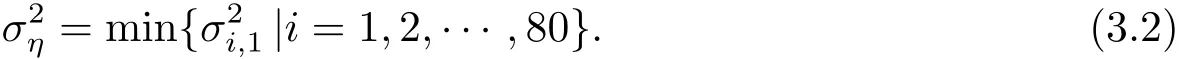
3.3 自適應非張量積小波緊框架圖像去噪算法

上文構造的基于二元六次樣條函數的非張量積小波緊框架具有81個二維濾波器,對圖像進行分解時可以獲得高頻部分80個方向上的信息[6],從而為圖像的處理提供了多通道上的信息,因此,在降噪過程中,更有利于刻畫圖像的細節和邊緣,便于后續的處理.通過自適應確定最優分解層數和閾值,進一步增強了算法的自適應性.

自適應非張量積小波緊框架圖像去噪的具體算法如下.

步驟1對于原始的灰度圖像I0,利用小波緊框架分解公式(2.3)實現圖像的第1層分解,得到第1層的近似系數D1和80個方向的細節系數,計算由公式(3.2)得到噪聲方差估計;

步驟3針對上述各層80個方向的細節系數,計算和βj,并運用公式(3.1)計算Tij,再對每層基于相應的閾值和軟閥值方法進行閾值量化,得到新的細節系數;

步驟4基于新的細節系數和末層的近似系數,利用小波緊框架重構公式(2.4)實現圖像的重構,得到去噪后的圖像I1.

4 圖像去噪的實例與結果分析

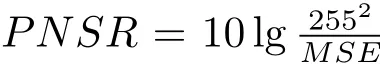
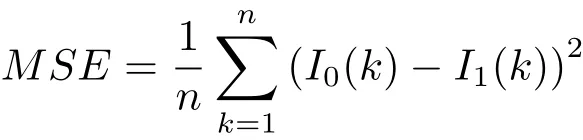
表示均方誤差,n是圖像的總像素個數,I0(k)和I1(k)分別表示去噪前后的圖像像素灰度值.

分別利用sym4小波(sym4_w)、db4小波(db4_w)、sym4小波包(sym4_wp)、db4小波包(db4_wp)、基于二元三次樣條函數的非張量積小波緊框架(23_ntptwf)和本文基于二元六次樣條函數的非張量積小波緊框架(26_ntptwf)對圖像進行去噪(其中前4種的分解層數為3層,選用NormalShrink自適應閾值算法;23_ntptwf的分解層數為2層,26_ntptwf經自適應確定最優分解層數為1層,采用本文改進的NormalShrink自適應閾值算法),其去噪效果如圖1所示,PNSR值如表1所示.從以上方法的去噪效果可以看出,sym4_w、db4_w、sym4_wp和db4_wp方法在去除噪聲的同時,缺乏對圖像細節和邊緣的保護使得去噪后的圖像過于模糊,23_ntptwf去噪效果有所改善.而利用本文所構造的26_ntptwf去噪,數值結果顯示,去噪效果優于前四種方法,其PNSR值也高于23_ntptwf.

針對本文提出的非張量積小波緊框架的最優分解層數自適應確定方法,為了顯示其有效性,除了自適應確定的最優分解層數1層,再分別選擇分解層數為2、3、4、5層,同時運用基于二元六次樣條函數的非張量積小波緊框架和本文改進的NormalShrink自適應閾值算法進行去噪,其效果如圖2所示,PNSR值如表2所示.可以看出,本文自適應確定的最優分解層數對應的去噪效果和PNSR值都優于其它分解層數.

圖1:幾種方法的去噪效果對比

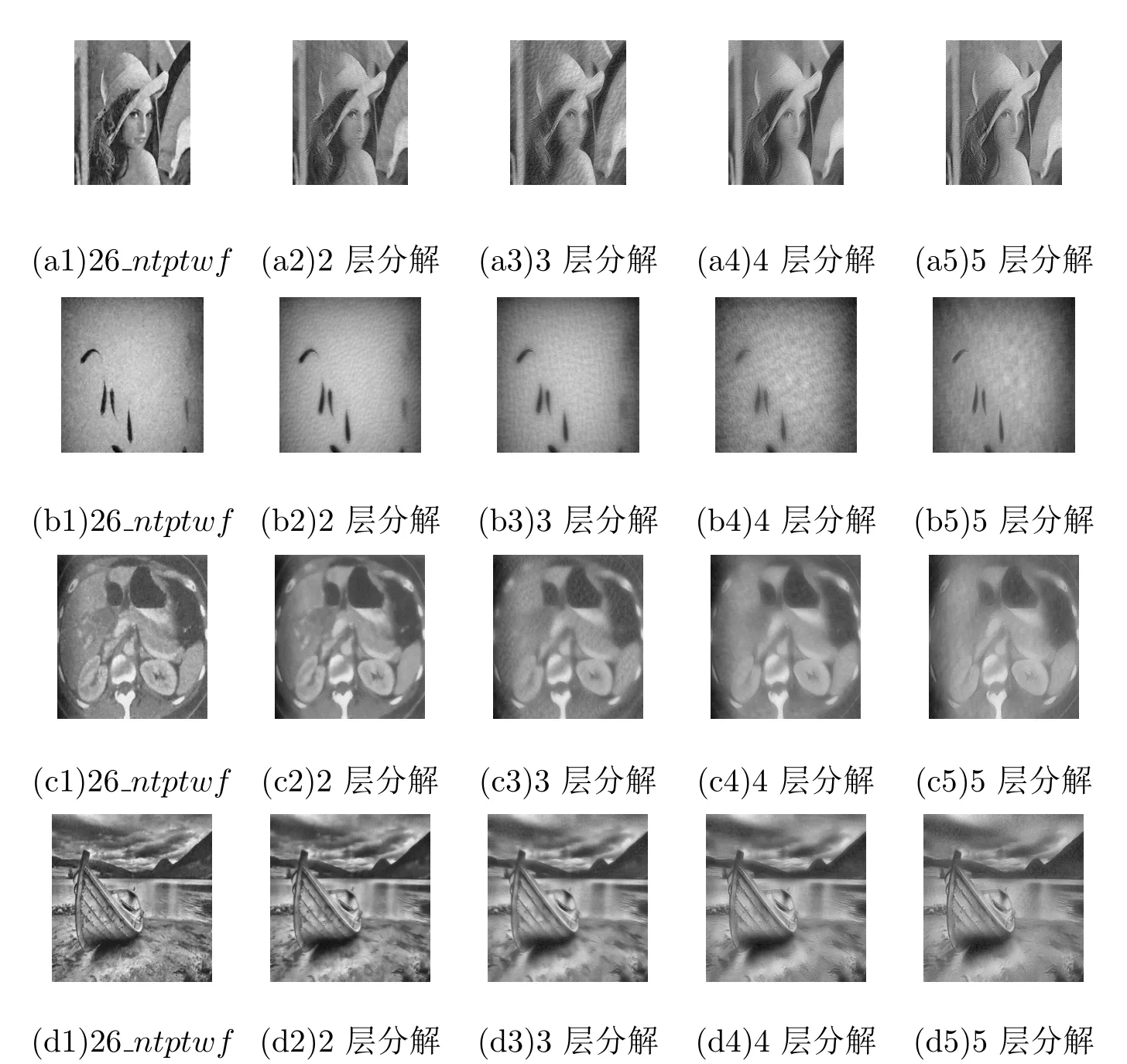
圖2:不同分解層數與最優分解層數的去噪效果對比

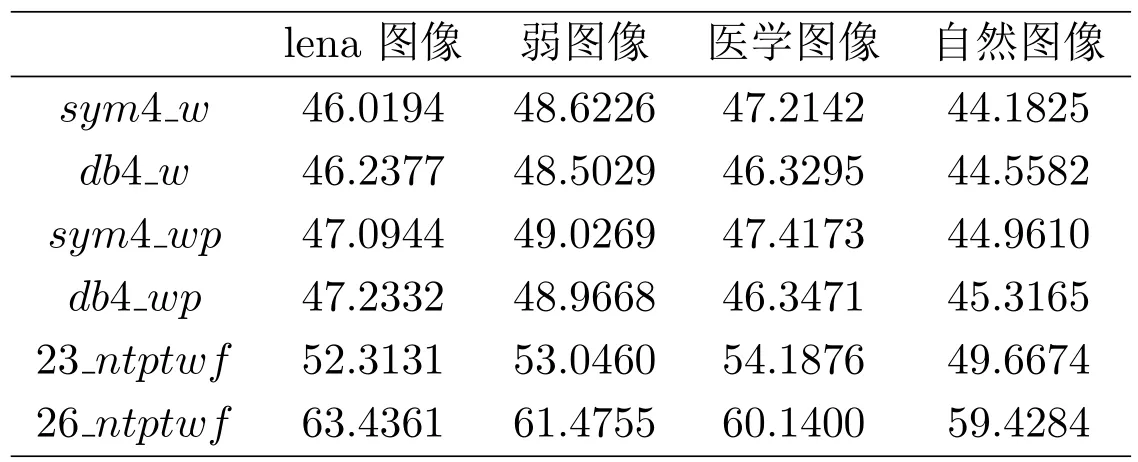
表1:幾種方法去噪的PNSR值對比

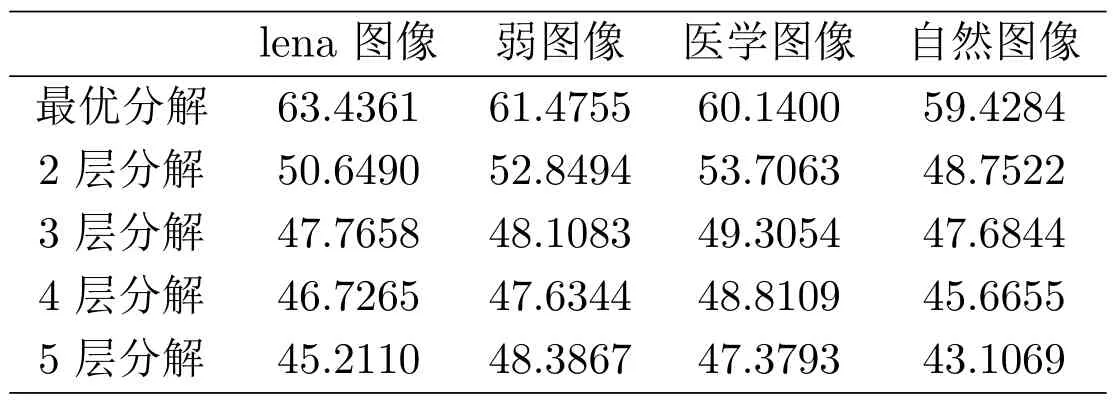
表2:不同分解層數與最優分解層數去噪的PNSR值對比

5 結語

本文針對圖像的去噪,構造了基于二元六次樣條函數的非張量積小波緊框架,而在框架分解層數和閾值的選取上,分別提出了基于香農熵自適應確定最優分解層數的方法和基于改進的NormalShrink自適應閾值算法,提高了算法的自適應性,在保證去噪效果的同時,實現了對圖像細節和邊緣的更好保護.

參考文獻

[1]Mantosh Biswas,Hari Om.An adaptive wavelet thresholding image denoising method[J].Nat.Conf.Comm.,2013:246–252.

[2]Bibina V C,Sanoj Viswasom.Adaptive wavelet thresholding and joint bilateral filtering for image denoising[J].Ann.IEEE India Conf.,2012:1100–1104.

[3]Fathi Abdolhossein,Naghsh-Nilchi.Efficient image denoising method based on a new adaptive wavelet packet thresholding function[J].IEEE Trans.Image Proc.,2012,21(9):3981–3990.

[4]Ron A,Shen Z W.Affine systems:the analysis of the analysis operator[J].J.Funct.Anal.,1997,148(2):408–447.

[5]Shen Z W,Xu Z Q.On B-spine framelets derived from the unitary extension principle[J].SIAM J.Math.Anal.,2012,45(1):127–151.

[6]陳聰,王仁宏.二元B-樣條構造非張量積緊框架及其應用[D].大連:大連理工大學,2013.

[7]王仁宏,崔錦泰.關于一個二元B-樣條基[J].中國科學(A輯),1984,9:784–795.

[8]王仁宏,施錫泉,羅鐘鉉,蘇志勛.多元樣條函數及其應用[M].北京:科學出版社,1994.

[9]蔡敦虎,羿旭明.小波基的選取對圖像去噪的影響[J].數學雜志,2005,25(2):185–190.