COMMON LIMIT DIRECTIONS OF JULIA SETS OF ENTIRE SOLUTIONS OF LINEAR DIFFERENTIAL EQUATIONS AND THEIR DERIVATIVES

SUN Gui-rong,YANG Yan-yan

(School of Mathematics and Physics,Suzhou University of Science and Technology,Suzhou 215009,China)

1 Introduction and Main Results

In this paper,we shall use the standard notations of Nevanlinna theory,its usual notations and basic results come mainly from[1–4].Now let f be a meromorphic function in the whole complex plane.We use λ(f)and μ(f)to denote the order and the lower order of f,respectively,which are de fined as[5,De finition 1.6]

De fine fn,n ∈ N as the nth iterate of f,that is,f1=f,···,fn=f ? (fn?1).The Fatou set F(f)of f is the subset of C whereforms a normal family,and its complement J(f)=CF(f)is called the Julia set of f.It is well known that F(f)is open and completely invariant under f,and J(f)is closed and non-empty.For an introduction to the dynamics of meromorphic functions,we refer the reader to see Bergweiler’s paper[6]and Zheng’s book[7].

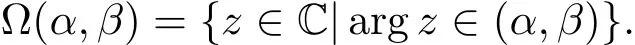
Assuming 0＜ α ＜ β ＜ 2π,we denote Given θ∈ [0,2π),if ?(θ? ε,θ+ ε)∩ J(f)is unbounded for every ε＞ 0,we say the radial argz=θ is a limit direction of J(f).De fine

Clearly,Δ(f)is closed and measurable,and we use mesΔ(f)to denote its linear measure.The research on the limit directions was initially studied by Baker(see[8]),where Baker proved that,for a transcendental entire function f,J(f)cannot lie in finitely many rays emanating from the origin.In[9],Qiao considered the limit directions of Julia sets of transcendental entire functions with finite lower order and obtained the following.

Theorem ALet f(z)be a transcendental entire function withμ(f)＜ ∞.Then mesΔ(f)=2π ifμ(f)＜ 1/2 and mesΔ(f)≥ π/μ(f)ifμ(f)≥ 1/2.

Naturally,a question arise here.

Question 1What can we say about the limit directions of Julia set of entire functions with in finite lower order?

Baker(see[8])constructed an entire function,for every M＞0,of in finite lower order satisfying

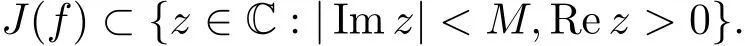
Thus Δ(f)={0}.Recently,Huang and Wang(see[10])investigated the limit directions of Julia sets of products of the solution base of the following equation(1.1).

Theorem BLet{f1,f2,···,fn}be a solution base of

where A(z)is a transcendental entire function with finite order,and denote E=f1f2···fn.Then

Actually,E(z)can be of in finite lower order in some cases.For example,for the equation f′′? (e2z+ez)f=0,we have μ(E(z))= ∞ (see[11,pp.394]).Later,Huang and Wang considered the limit directions of Julia sets of solutions of linear differential equations directly.

Theorem C(see[12])Let Ai(z)(i=0,1,···,n?1)be entire functions of finite lower order such that A0is transcendental and m(r,Ai)=o(m(r,A0))(i=1,2,···,n ? 1)as r→∞.Then every non-trivial solution f of the equation

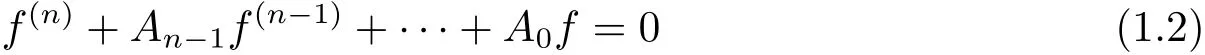
satis fies mesΔ(f)≥ min{2π,π/μ(A0)}.

Clearly,by the lemma of logarithmic derivatives,each non-trivial solution f(z)in Theorem C must have in finite lower order.Theorems B and C,therefore,obtain some results about the limit directions of Julia sets for some classes of entire functions of in finite lower order.

In this paper,we continue to discuss Question 1.Moreover,we will investigate the common limit directions of transcendental entire functions with in finite lower order and their derivatives.

Theorem 1.1Let A0(z),···,An?1(z),A0(z)0 be entire functions such that for real constants a,b,c,θ1,θ2,where 0 ≤ a ＜ b,c＞ 0 and θ1＜ θ2,we have

and

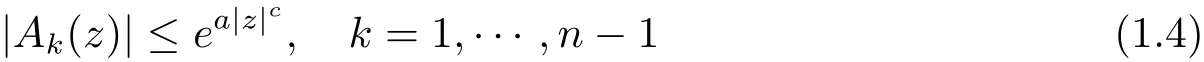
as z → ∞ with θ1≤ argz ≤ θ2.If f is a non-trivial solution of equation(1.2),then mes

Before we prove Theorem 1.1,we need to prove the next result.

Theorem 1.2Under the hypothesis of Theorem 1.1,every solution f(/≡0)of equation(1.2)satis fies mesΔ(f)≥ θ2? θ1.

Remark 1Clearly from Lemma 2.4 in Section 2,each non-trivial solution of(1.2)has in finite order.Next,we will give an example to show that the entire solutions of(1.2)can be of in finite lower order in some cases.In addition,we note that both Theorems B and C require that there is a dominant coefficient whose growth of order is greater than the other coefficients,while all the coefficients in our theorems may have the same order.

ExampleConsider the differential equation

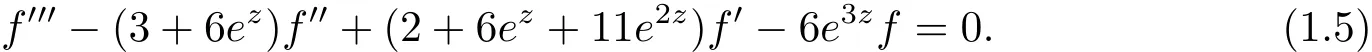
Clearly,the three linearly independent functions

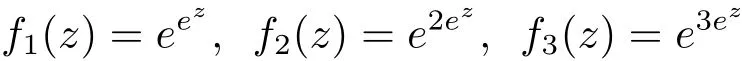
are solutions of(1.5)with μ(f1)= μ(f2)= μ(f3)= ∞ and σ(A0)= σ(A1)= σ(A2).

Remark 2Some results about common limit directions of transcendental entire functions and their derivatives were obtained by Qiao(see[13]).He proved that for transcendental entire functions of finite lower order and their derivatives,there exist a large amount of common limit directions.Wang[14]obtained some similar results for the case of transcendental meromorphic functions with finite lower order.By using the method of[12,14],Sun(see[15])and Zhang(see[16,17])obtained some results for solutions to some special classes of linear differential equations.

2 Preliminary Lemmas

In order to prove our Theorem,we first recall the Nevanlinna Characteristic in an angle,see[1].We denote by(α,β)the closure of ?(α,β),and set

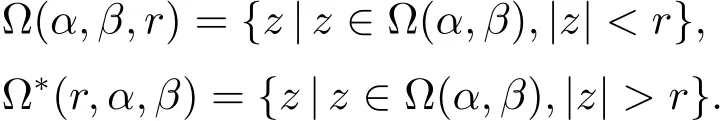
Let g(z)be meromorphic on the angle ?(α,β)where β?α ∈ (0,2π].Following[1],we de fine

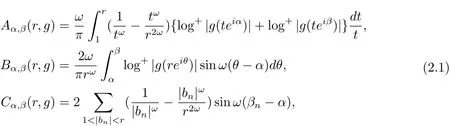
where ω = π/(β ? α),andare the poles of g(z)in(α,β)appeared according to their multiplicities.The Nevanlinna angular characteristic is de fined as follows:

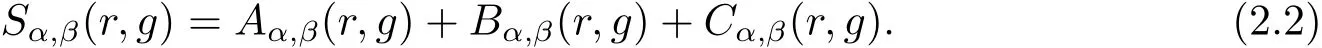
Especially,we use

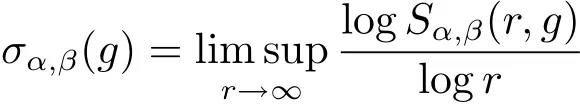
to denote the order of Sα,β(r,g).

We say an open set hyperbolic if it has at least three boundary points inLet W be a hyperbolic open set in C.For an a∈CW,de fine

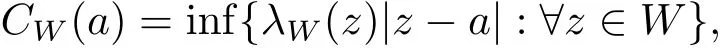
where λW(z)is the hyperbolic density on W.It is well known that if every component of W is simply connected,then CW(a)≥1/2.

Lemma 2.1(see[7,10])Let f(z)be analytic in ??(r0,θ1,θ2),U be a hyperbolic domain and f:??(r0,θ1,θ2)→ U.If there exists a point a ∈ ?U{∞},such that CU(a)＞ 0,then there exists a constant d＞ 0 such that for sufficiently small∈＞0,we have

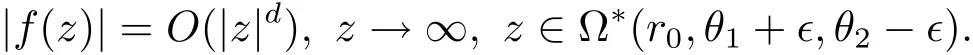
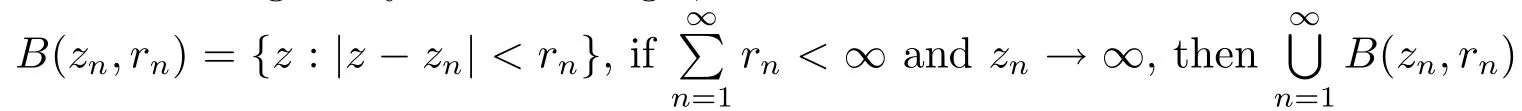
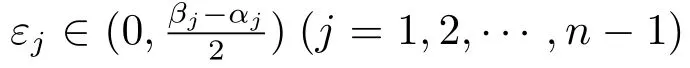
there exist K ＞ 0,M ＞ 0 only depending on g,ε1,···,εn?1and ?(αn?1,βn?1),and not depending on z such that

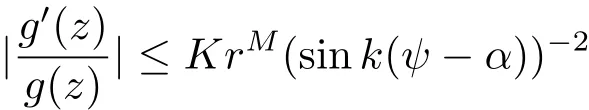
and

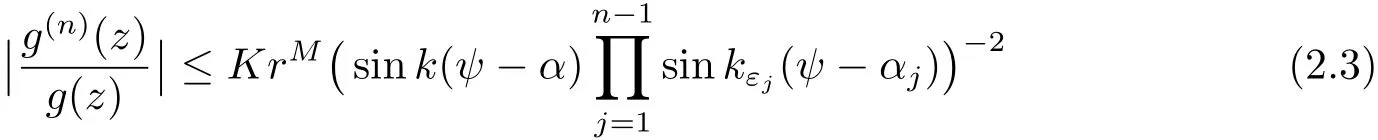
for all z ∈ ?(αn?1,βn?1)outside an R-set D,where k= π/(β?α)and kεj= π/(βj?αj)(j=1,2,···,n ? 1).

Lemma 2.3(see[18])If f is transcendental and entire,then F(f)has no unbounded multi-connected component.

Lemma 2.4(see[19])Let A0(z),···,An?1(z),A0(z)0 be entire functions such that for real constants α,β,μ,θ1,θ2,where 0 ≤ β ＜ α,μ ＞ 0 and θ1＜ θ2,we have

and

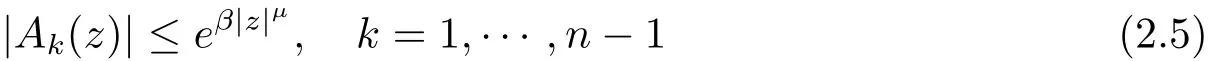
as z → ∞ with θ1≤ argz ≤ θ2.Then every solution f/≡ 0 equation(1.2)has in finite order.

3 Proof of Theorem 1.2

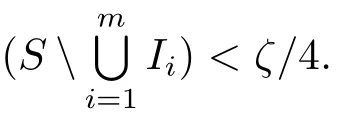
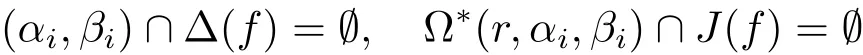
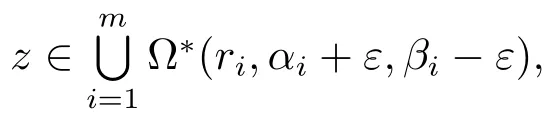
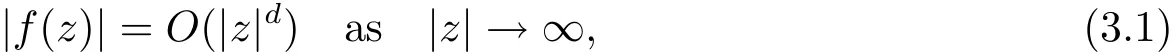
where 0 ＜ ε＜ min{ζ/(16m),(βi? αi)/8,i=1,2,···,m}.Thus,recall the de finition of Sα,β(r,f),we immediately see

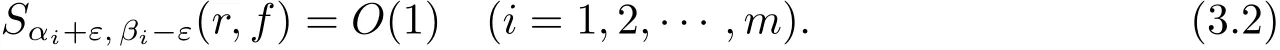
Therefore by Lemma 2.2,there exists two constants M＞0 and K＞0 such that

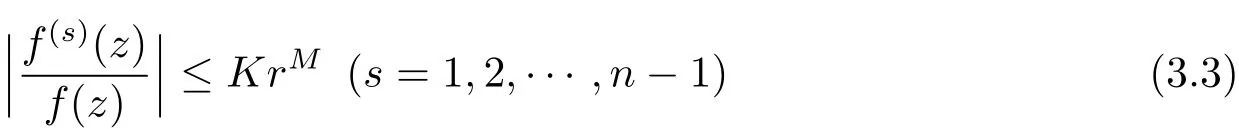
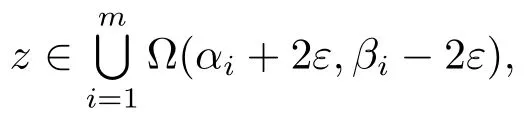
Set D=(θ1,θ2).Clearly,

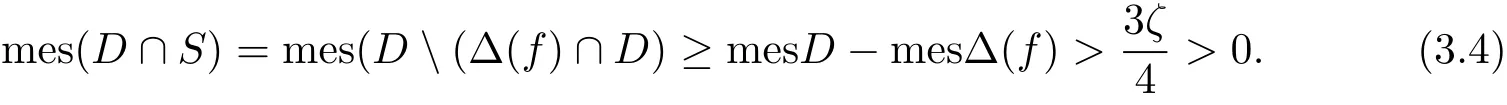
Therefore

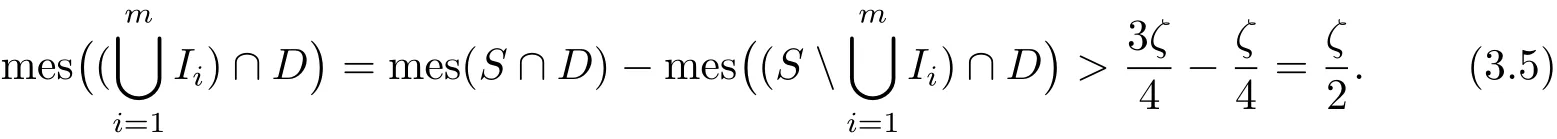
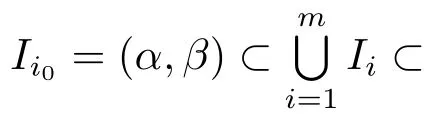
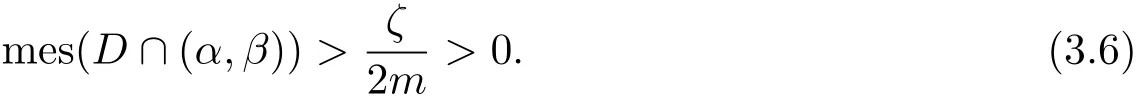
Then,for sufficiently large r,

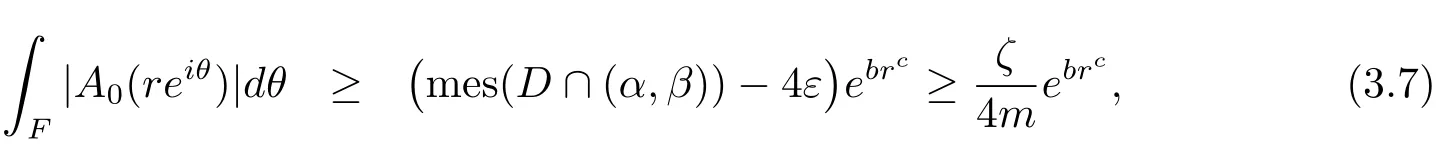
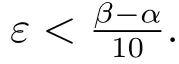
On the other hand,coupling(1.2)and(3.3)leads

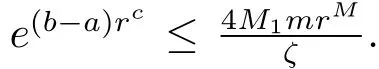
4 Proof of Theorem 1.1

Conversely,assume that mes(Δ(f)∩Δ(f(k)))＜ θ2?θ1,and set ζ= θ2?θ1?mes(Δ(f)∩Δ(f(k))).Next,we will find an interval I such that I(Δ(f)∩ Δ(f(k))satisfying I ?Δ(f(k))Cand I ? Δ(f),where Δ(f(k))C=[0,2π)Δ(f(k)),and obtain the assertion by reduction to a contradiction in this interval.Set D=(θ1,θ2).

Step 1In this step,we shall prove that mes(DΔ(f))=0.Otherwise,since D is open and Δ(f)is closed,we can find a ray argz= θ0such that θ0Δ(f)and there exists some positive constant η such that(θ0? η,θ0+ η)? D and ??(r,θ0? η,θ0+ η)∩ J(f)= ? for sufficiently large r.Then following similar discussion as in Theorem 1.1,we have(3.1)holds for ??(r,θ0? η,θ0+ η).Therefore it follows that

where F1=D ∩ (α,β)and M2is a constant.

On the other hand,

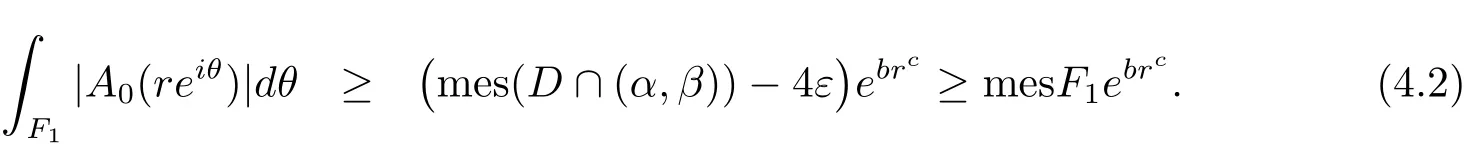
(4.1)and(4.2)lead to a contradiction.

Step 2From Theorem 1.2,we already know

And from Step 1,we have

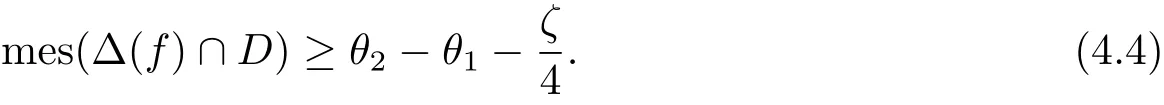
Since Δ(f(k))is closed,clearly S=(0,2π) Δ(f(k))is open,so it consists of at most countably many open intervals.We can choose finitely many open intervals Ii=(αi,βi)(i=1,2,···,m)satisfying

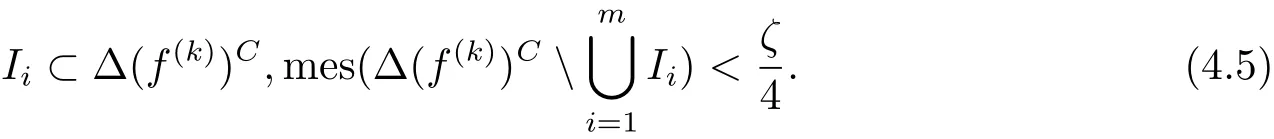
Thus for sufficiently large r,

and hence

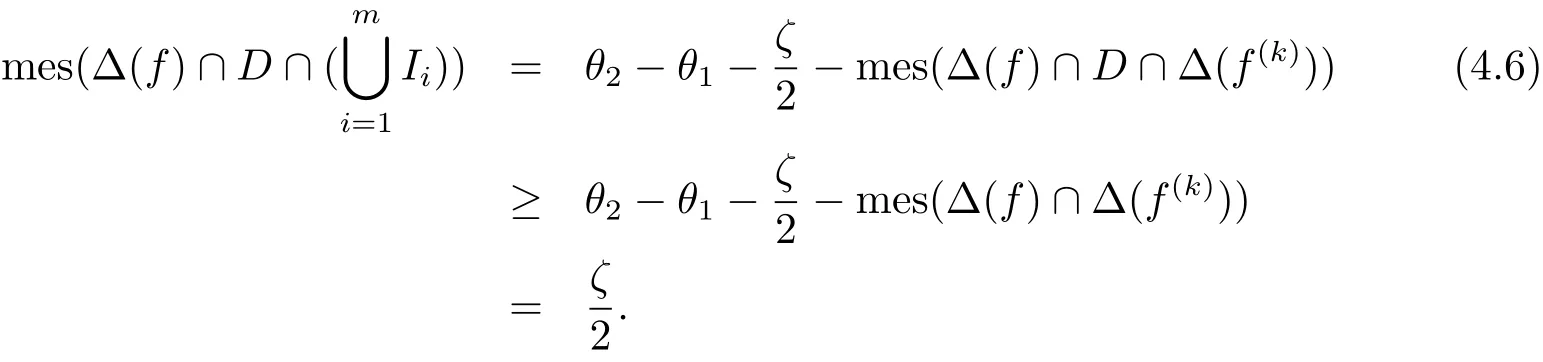
Therefore there exist some Iisuch that

Thus we can choose a ray argz= θ and sufficiently small η ＞ 0 such that(θ?η,θ+η)? Iiand

For the angular domain ?(θ?η,θ+η),it is easy to see

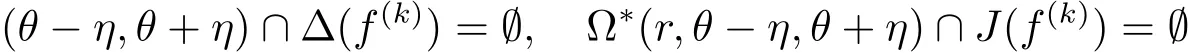
for sufficiently large r.This implies that there exist the corresponding riand unbounded Fatou component U of F(f(k))such that ??(r,θ? η,θ+ η) ? U,see[18].We take an unbounded and connected section Γ of?U,then the mapping f(k):??(r,θ?η,θ+η)→ CΓ is analytic.Since we have chosen Γ such that CΓ is simply connected,so for any a ∈ Γ{∞},we have CCΓ(a)≥ 1/2.Applying Lemma 2.1 to f(k)in every ??(r,θ?η,θ+η),there exists a positive constant d and R such that for z ∈ ??(R,θ? η,θ+η),

For z=reiθ∈ ??(R,θ? η,θ+ η),take a curve γ which connecting Reiθto reiθalong argz=θj.So we deduce from(4.9)that

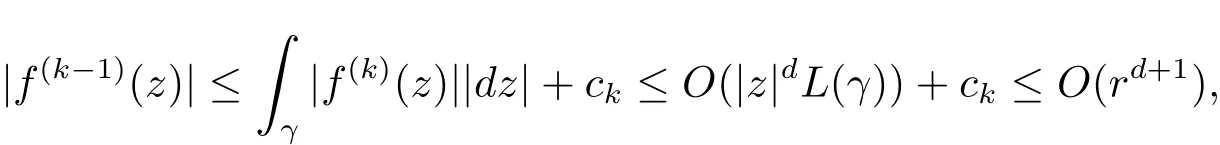
where L(γ)denotes the length of γ.Similarly,we have

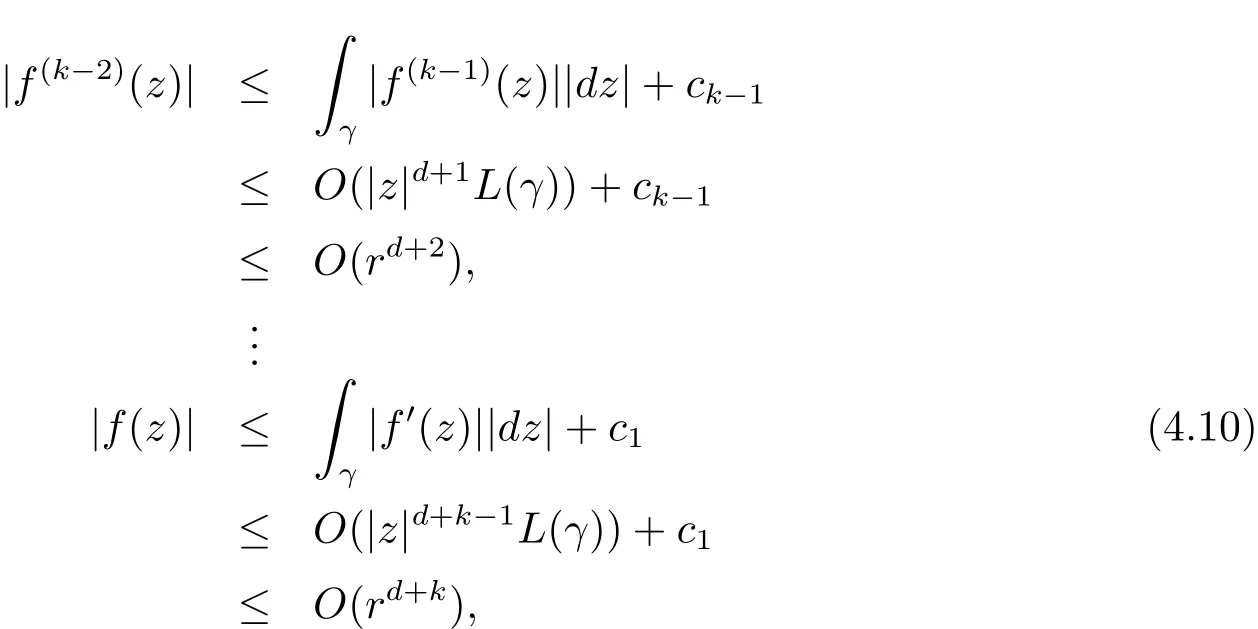
where c1,c2,···,ckare constants.Therefore,by the de finition of Sα,β(r,f),we immediately see

Then by Lemma 2.2,there exists two constants M＞0 and K＞0 such that

for all z∈ ?(θ?η,θ+η),outside a R-set H1.

It follows from(1.3)that

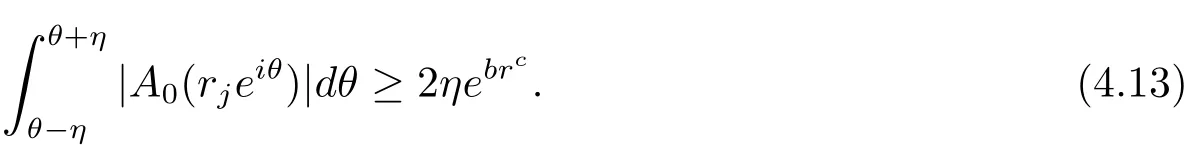
On the other hand,coupling(1.2)and(4.12)leads

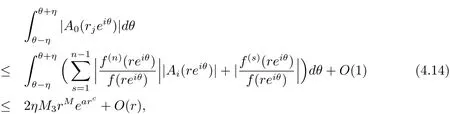
where M3is a constant.By(4.13)and(4.14),we can obtain a contradiction since b＞a≥0.

References

[1]Goldberg A A,Ostrovskii I V.Value distribution of meromorphic functions[M].American:Transl.Math.Monographs Amer.,Amer.Math.Soc.,2008.

[2]Hayman W K.Meromorphic functions[M].Oxford:Clarendon Press,1964.

[3]Laine I.Nevanlinna theory and complex differential equations[M].Berlin:de Gruyter,1993.

[4]Huang Zhigang.Some dynamical properties of transcendental entire functions[J].J.Math.,2011,31(6):1024–1030.

[5]Yang Chungchun,Yi Hongxun.Uniqueness theory of meromorphic functions[M].Dordrecht:Kluwer,2003.

[6]Bergweiler W.Iteration of meromorphic functions[J].Bull.Amer.Math.Soc.,1993,29(2):151–188.

[7]Zheng Jianhua.Dynamics of transcendental meromorphic functions(Chinese)[M].Monograph of Tsinghua University,Beijing:Tsinghua Univ.Press,2006.

[8]Baker I N.Sets of non-normality in iteration theory[J].J.London Math.Soc.,1965,40(1):499–502.

[9]Qiao Jianyong.Stable domains in the iteration of entire functions(Chinese)[J].Acta.Math.Sinica.,1994,37(5):702–708.

[10]Huang Zhigang,Wang Jun.On the radial distribution of Julia sets of entire solutions of f(k)+A(z)f=0[J].J.Math.Anal.Appl.,2012,387(2):1106–1113.

[11]Bank S,Laine I.On the oscillation theory of f′′+Af=0 where A is entire[J].Trans.Amer.Math.Soc.,1982,273(1):351–363.

[12]Huang Zhigang,Wang Jun.On the limit directions of Julia sets of entire solutions of linear differential equations[J].J.Math.Anal.Appl.,2014,409(1):478–484.

[13]Qiao Jianyong.On limiting directions of Julia sets[J].Ann.Acad.Sci.Fenn.Math.,2001,26(2):391–399.

[14]Wang Sheng.On radial distribution of Julia sets of meromorphic functions[J].Taiwanese J.Math.,2007,11(5):1301–1313.

[15]Sun Guirong,Huang Zhigang.Radial distributions of Julia sets of meromorphic solutions of linear differential equations[J].J.Math.,2015,35(6):1393–1399.

[16]Zhang Guowei,Wang Jian,Yang Lianzhong.On radial distribution of Julia sets of solutions to certain second order complex linear differential equations[J].Abs.Appl.Anal.,2014,3:444–468.

[17]Zhang Guowei,Wang Jian,Yang Lianzhong.Radial distribution of Julia sets of derivatives of solutions of complex linear differential equations[J].Sci.China,2014,44(6):693–700.

[18]Baker I N.The domains of normality of an entire function[J].Ann.Acad.Sci.Fenn.Ser.A I Math.,1975,1(2):277–283.

[19]Belaidi B,Hamouda S.Orders of solutions of an n-th order linear differential equation with entire coefficients[J].Elec.J.Diff.Equ.,2001,61:1–5.