COMMUTATORS GENERATED BY LUSIN-AREA INTEGRAL AND LOCAL CAMPANATO FUNCTIONS ON GENERALIZED LOCAL MORREY SPACES

MO Hui-xia,MA Rui-qing,WANG Xiao-juan

(School of Science,Beijing University of Posts and Telecommunications,Beijing 100876,China)

1 Introduction

Suppose that Sn?1is the unit sphere in Rn(n ≥ 2)equipped with the normalized Lebesgue measure dσ.Let ? ∈ Ls(Sn?1)(1＜s≤∞)be homogeneous of degree zero and satisfy the cancellation condition

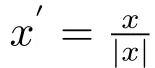
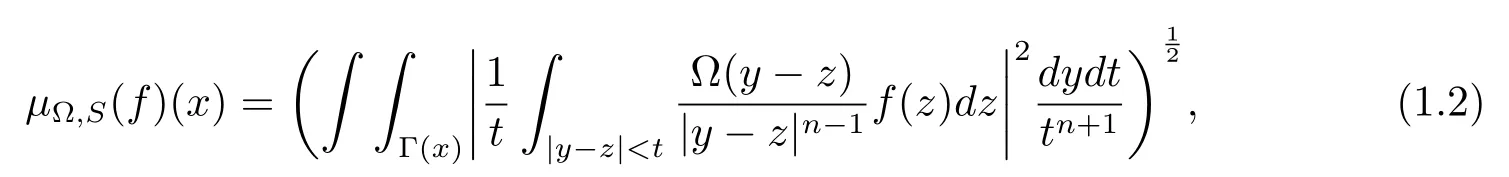
where

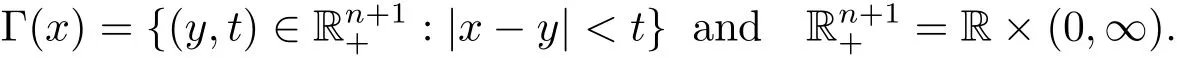
Moreover,letwhere bi∈ Lloc(Rn)for 1 ≤ i≤ m.Then the multilinear commutator generated byand μ?,Scan be de fined as follows:

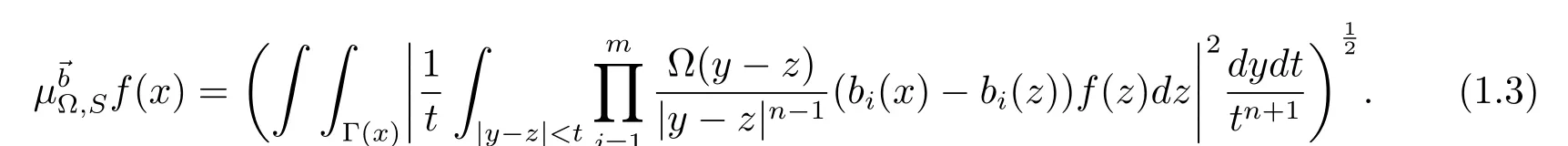
It is well known that the Lusin-area integral plays an important role in harmonic analysis and PDE(for example,see[1–8]).Therefore,it is a very interesting problem to discuss the boundedness of the Lusin-area integral.In[2],Ding,Fan and Pan studied the weighted Lpboundedness of the area integralμ?,S.In[3],the authors investigated the boundeness ofμ?,Son the weighted Morrey spaces.The commutators generated by μ?,Sattracted much attention too.In[5]and[6],the authors discussed the weighted Lpboundedness and endpoint estimates for the higher order commutators generated by μ?,Sand BMO function,respectively.In[8],the authors showed that the commutator generated by μ?,Sand V MO is a compact operator in the Morrey space.

Moreover,the classical Morrey space Mp,λwere first introduced by Morrey in[9]to study the local behavior of solutions to second order elliptic partial differential equations.And,in[10],the authors introduced the local generalized Morrey spaceand they also studied the boundedness of the homogeneous singular integrals with rough kernel on these spaces.

Motivated by the works of[2,3,5,8,10,13],we are going to consider the boundedness ofμ?,Son the local generalized Morrey spaceas well as the boundedness of the commutators generated by μ?,Sand local Campanato functions.

2 Some De finitions and Lemmas

De finition 2.1[10]Let ?(x,r)be a positive measurable function on Rn× (0,∞)and 1≤p≤∞.For any fixed x0∈Rn,a function fis said to belong to the local Morrey space,if

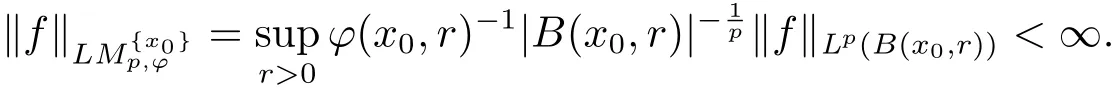
And we denote

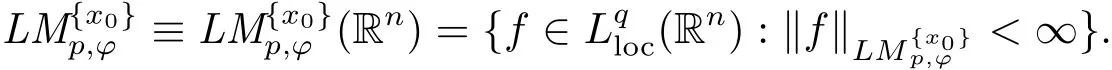
According to this de finition,we recover the local Morrey spaceunder the choice

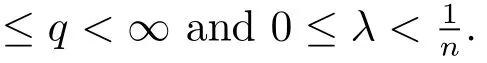
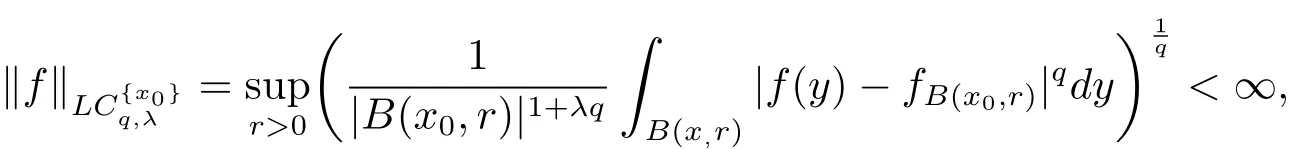
where

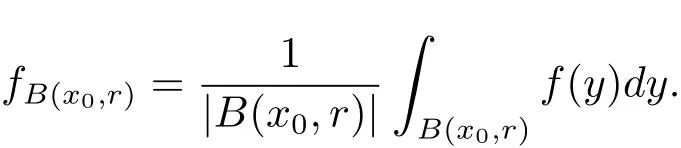
De fine

Remark 2.1[10]Note that,the central BMO spaceandMoreover,imagining that the behavior ofmay be quite different from that of BMO(Rn),since there is no analogy of the John-Nirenberg inequality of BMO for the space

Lemma 2.1[10]Let 1then

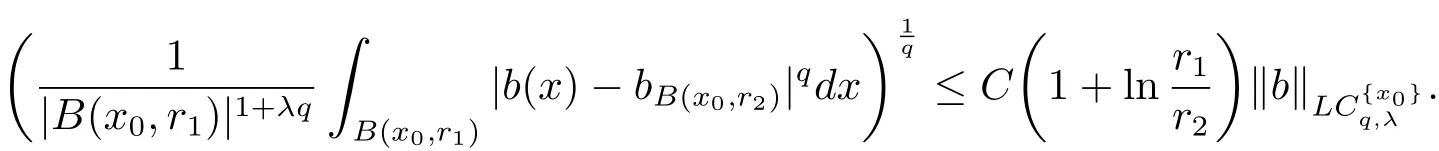
And from this inequality,we have

In this section,we are going to use the following statement on the boundedness of the weighted Hardy operator

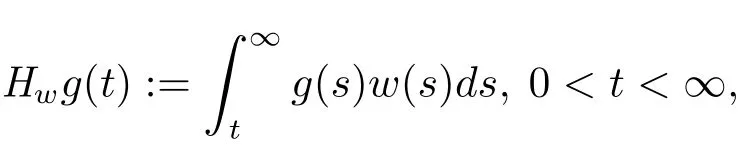
where w is a fixed function non-negative and measurable on(0,∞).

Lemma 2.2[11,12]Let v1,v2and w be positive almost everywhere and measurable functions on(0,∞).The inequality

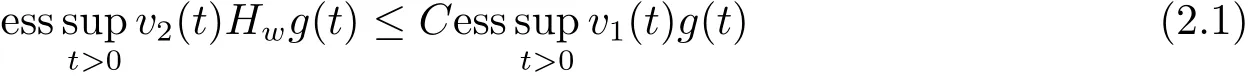
holds for some C＞0 and all non-negative and non-decreasing g on(0,∞)if and only if

Moreover,ifis the minimum value of C in(2.1),then=B.

Lemma 2.3[2]Suppose that 1＜ q,s≤ ∞ and ? ∈ Ls(Sn?1)satisfying(1.1).If q,s and weighted function w satisfy one of the following conditions

(i)max{s′,2}= η ＜ q ＜ ∞,and w ∈ Aq/η;

(ii)2 ＜ q ＜ s,and w1?(q/2)′∈ Aq′/s′;

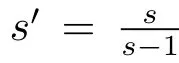
Remark 2.2From Lemma 2.3,it’s obvious that when ? ∈ Ls(Sn?1)(1 ＜ s ≤ ∞)satis fies condition(1.1),the operatorμ?,Sis bounded on Lq(Rn)space for 2≤ q＜ ∞.

3 Lusin-Area Integral on Generalized Local Morrey Spaces

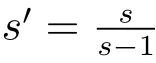
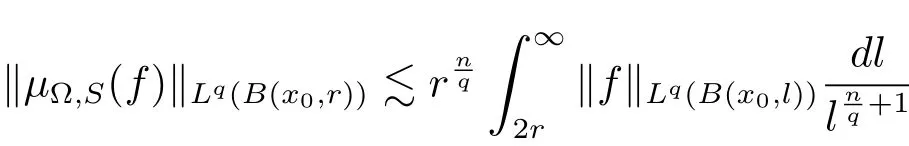
holds for any ball B(x0,r).

ProofLet B=B(x0,r).We write f=f1+f2,where f1=fχ2Band f2=fχ(2B)c.Thus we have

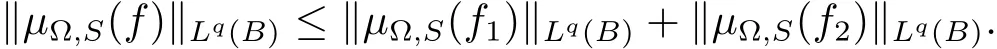
Since μ?,Sis bounded on Lq(Rn)space(see Lemma 2.3),then it follows that

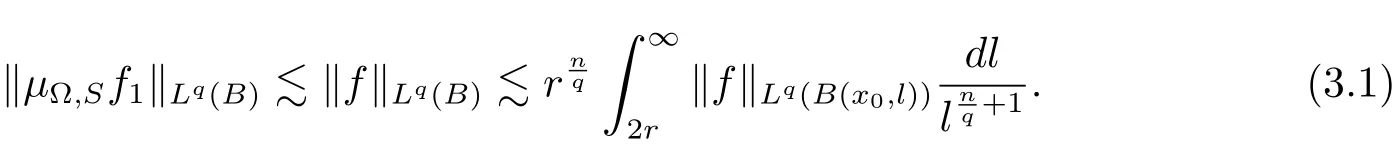
Our attention will be focused now on

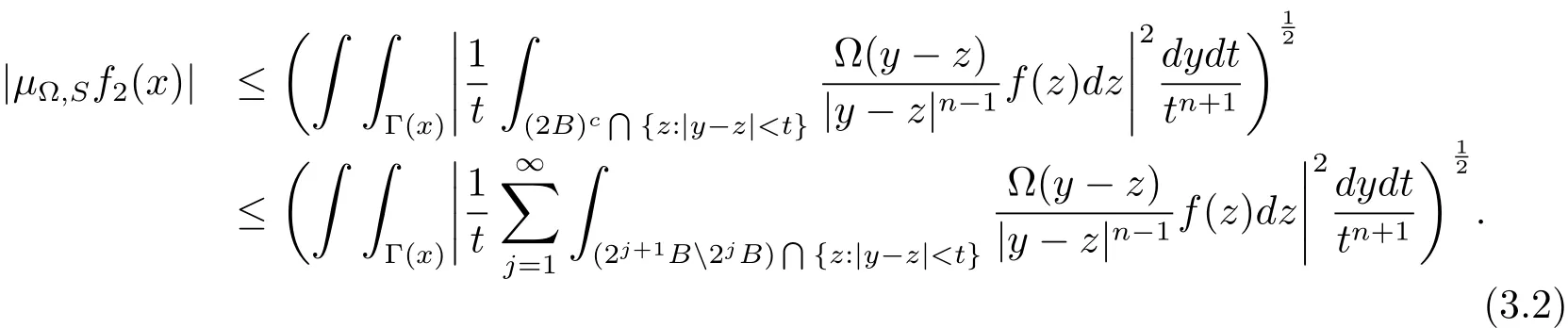
Without loss of generality,we can assume that for any x∈B,(y,t)∈Γ(x)and z∈2j+1B2jB,we haveThus there existssuch that

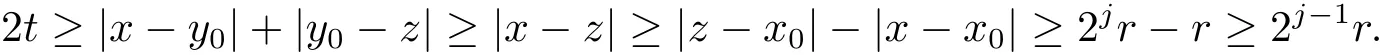
Hence

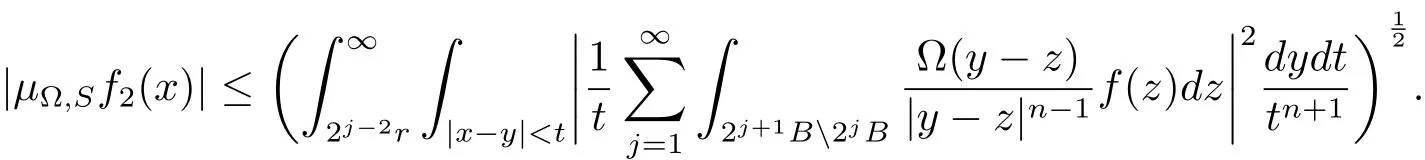
When ? ∈ L∞(Sn?1),it follows from the Hlder’s inequality that

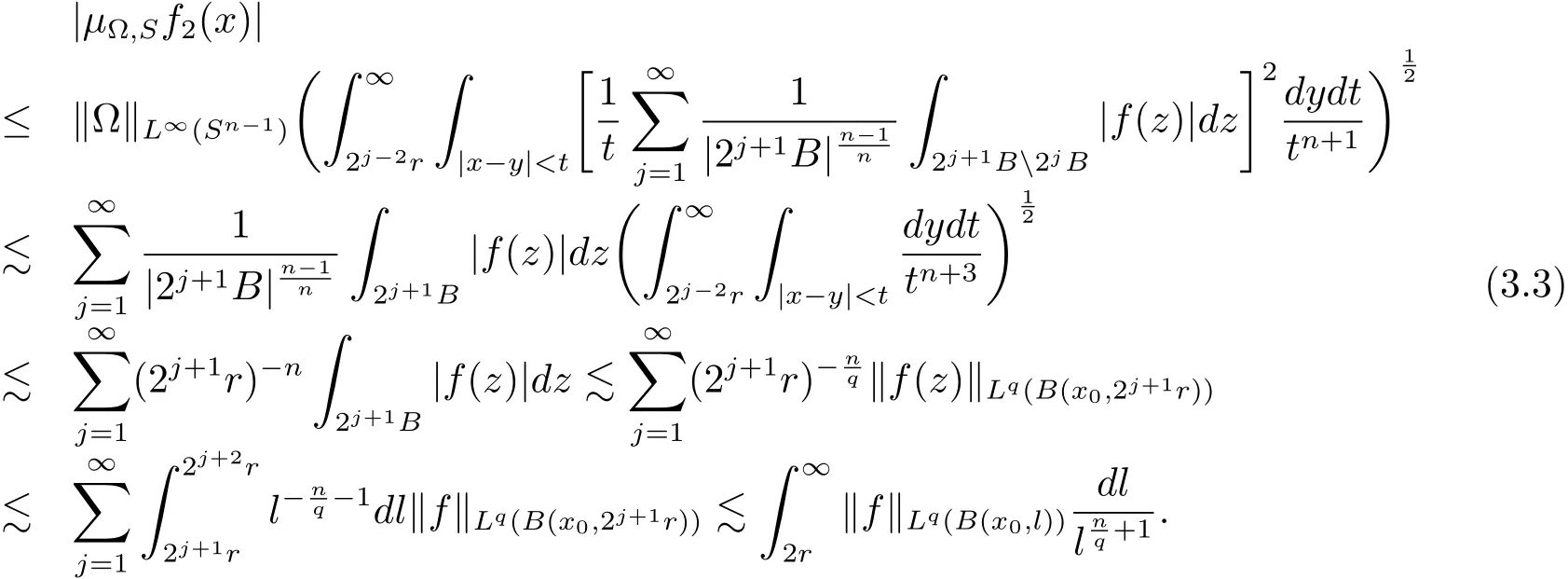
When ? ∈ Ls(Sn?1),1 ＜ s ＜ ∞,it is obvious that

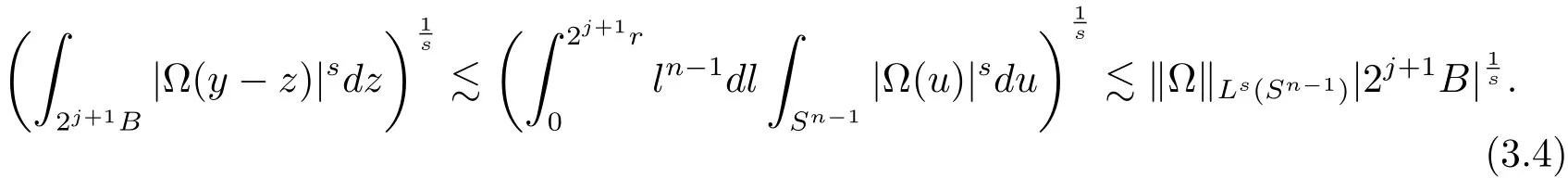
Thus from H?lder’s inequality and(3.4),we have

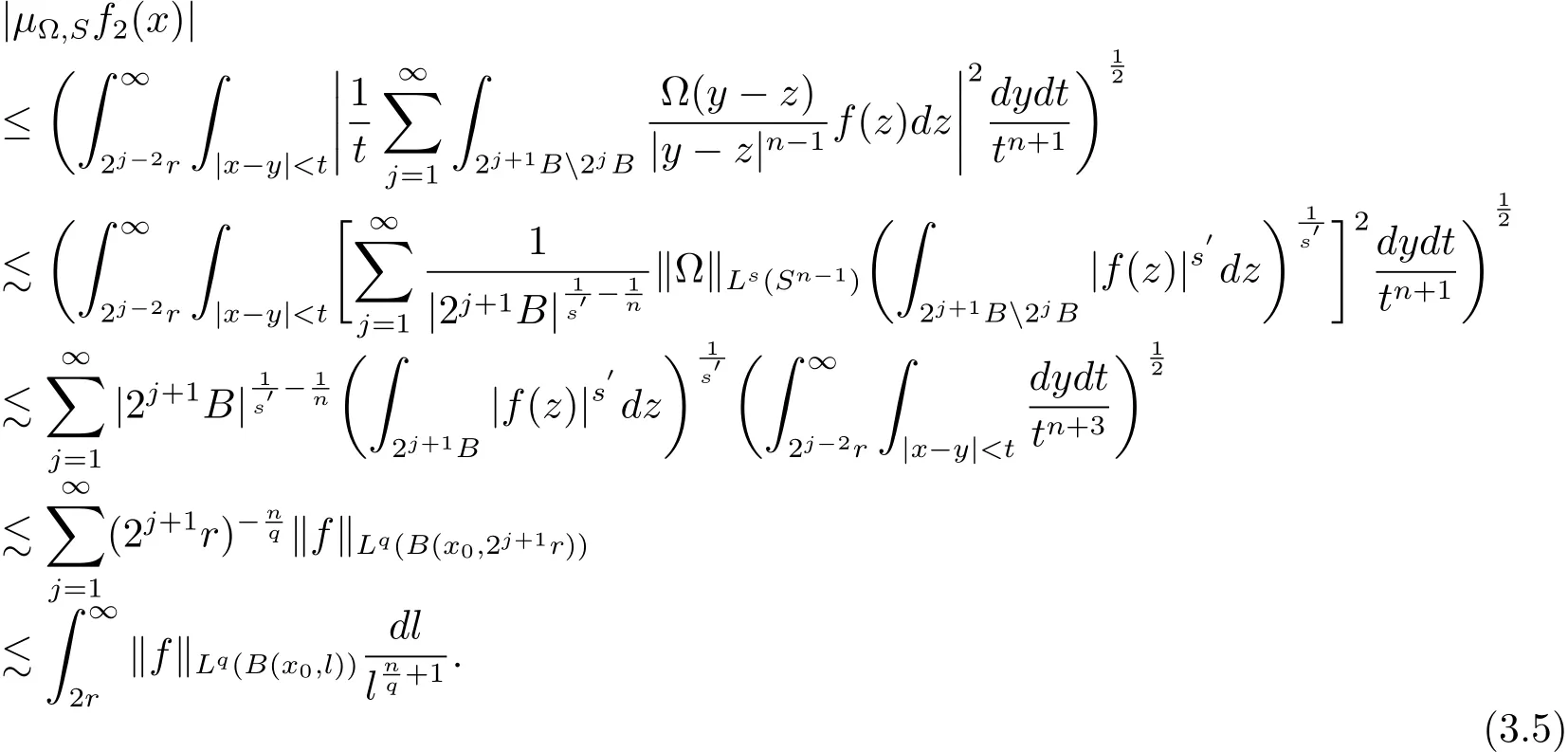
So

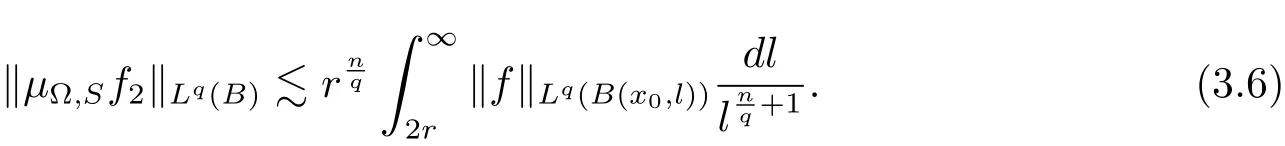
Therefore combining(3.1)and(3.6),we have

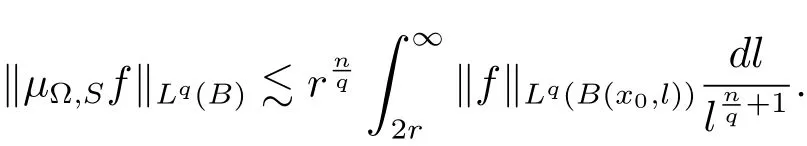
Thus we complete the proof of Theorem 3.1.

Theorem 3.2Let ? ∈ Ls(Sn?1)(1 ＜ s ≤ ∞)satisfy condition(1.1)and max{2,s′} ＜q＜ ∞.Then,if functions ?,ψ :Rn×(0,∞)→ (0,+∞)satisfy the inequality

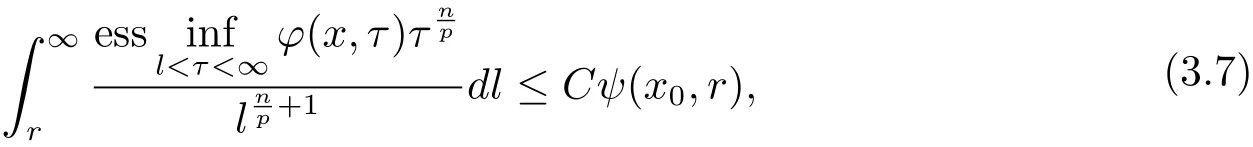
where C does not depend on x and r,the operatorμ?,Sis bounded from

ProofTakingandthen from Theorem 3.1,we have

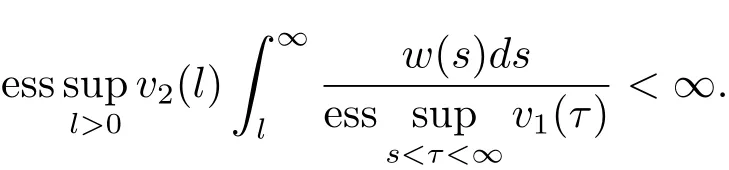
Thus from Lemma 2.2,it follows that

Therefore

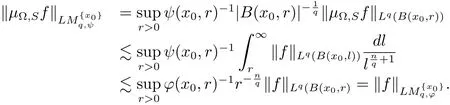
Thus we complete the proof of Theorem 3.2.

4 Commutators Generated by Lusin-Area Integral on Generalized Local Morrey Spaces

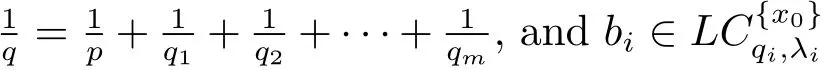
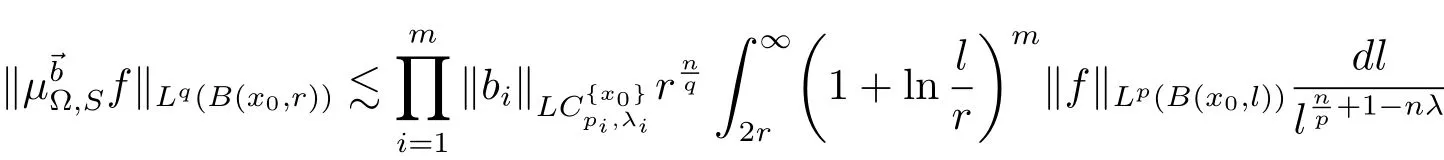
holds for any ball B(x0,r),where λ = λ1+ λ2+ ···+ λm.

ProofWithout loss of generality,it is sufficient for us to show that the conclusion holds for m=2.

Let B=B(x0,r).And we write f=f1+f2,whereThus we have

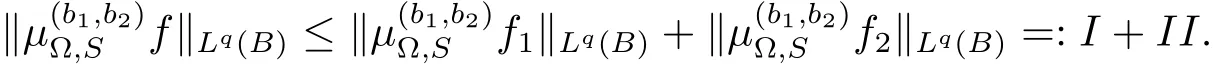
Let us estimate I and II,respectively.It is obvious that

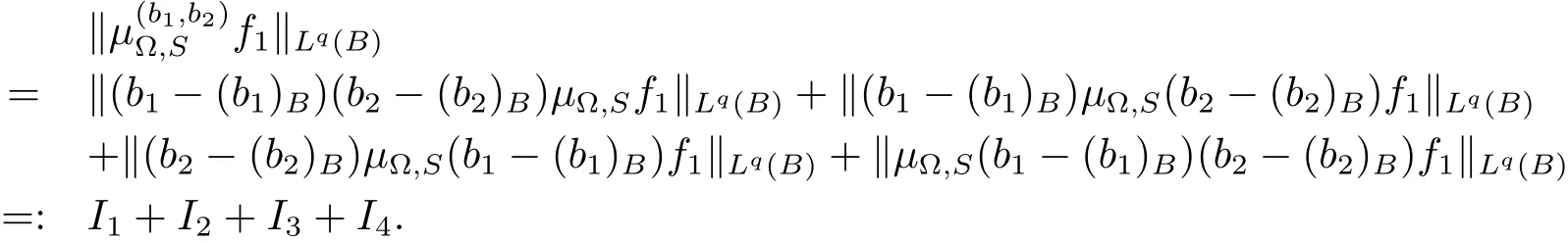
From Lemma 2.1,it is easy to see that

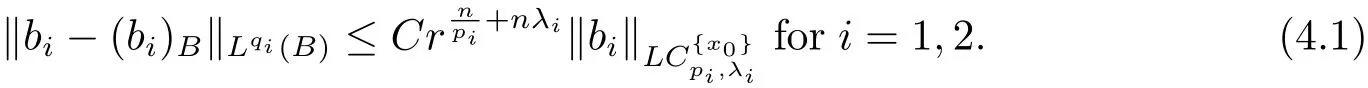
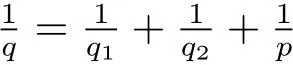
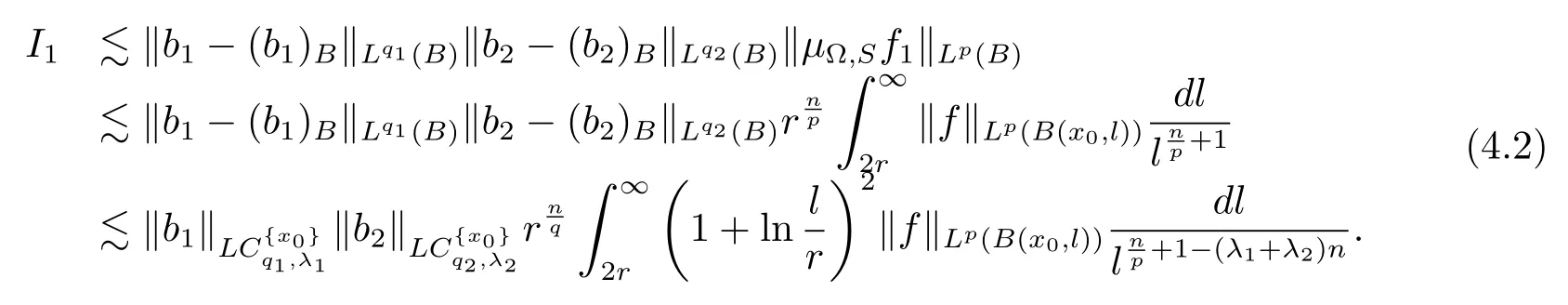
Moreover,from Lemma 2.1,it is easy to see that

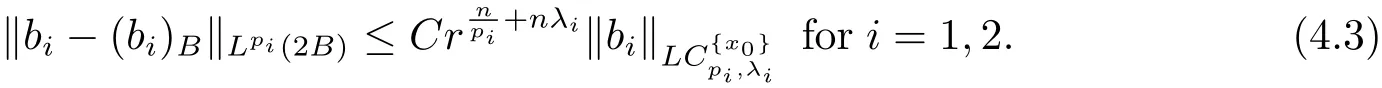
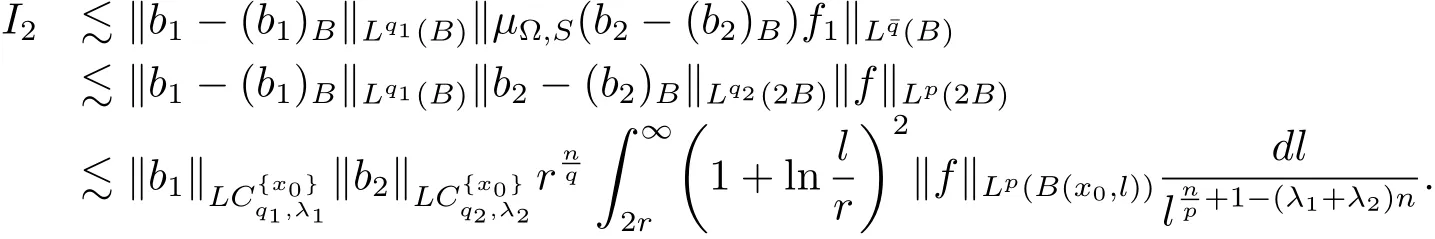
Similarly,

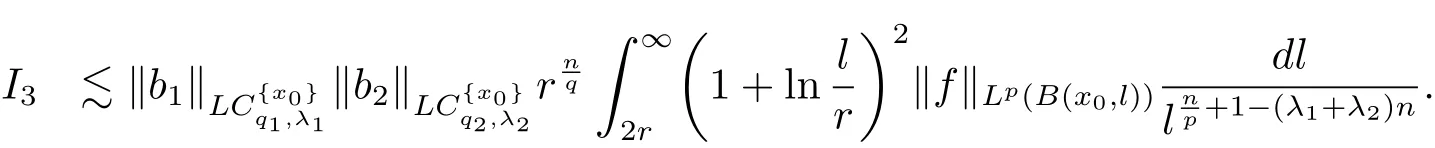
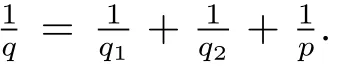
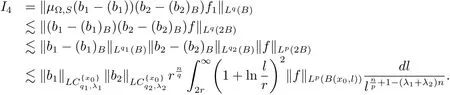
Therefore combining the estimates of I1,I2,I3and I4,we have

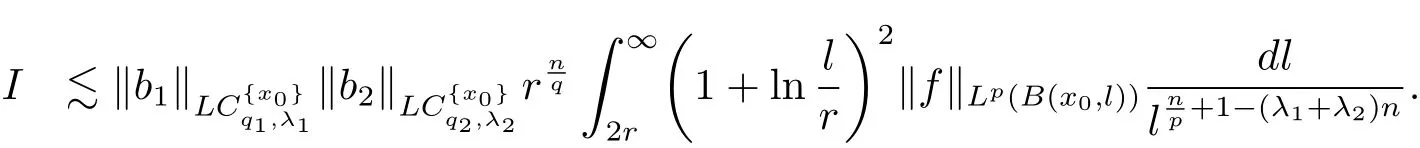
Let us estimate II.

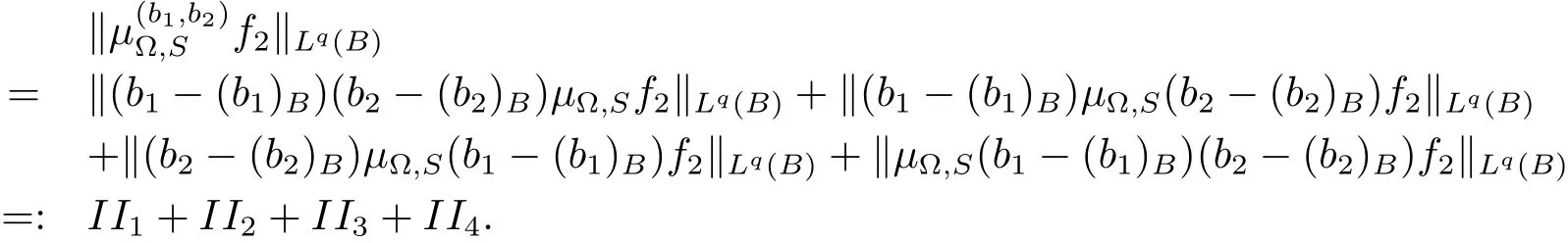
SinceThen using H?lder’s inequality and(3.6),we have

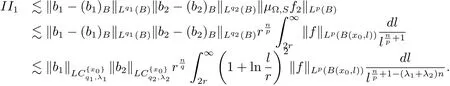
In the following,let us estimate II2.For x ∈ B,when ? ∈ L∞(Sn?1),from Lemma 2.1 and estimate of(3.3),we have

For x∈B,when ? ∈ Ls(Sn?1),1＜ s＜ ∞,from Lemma 2.1 and the estimate of(3.5),it follows that

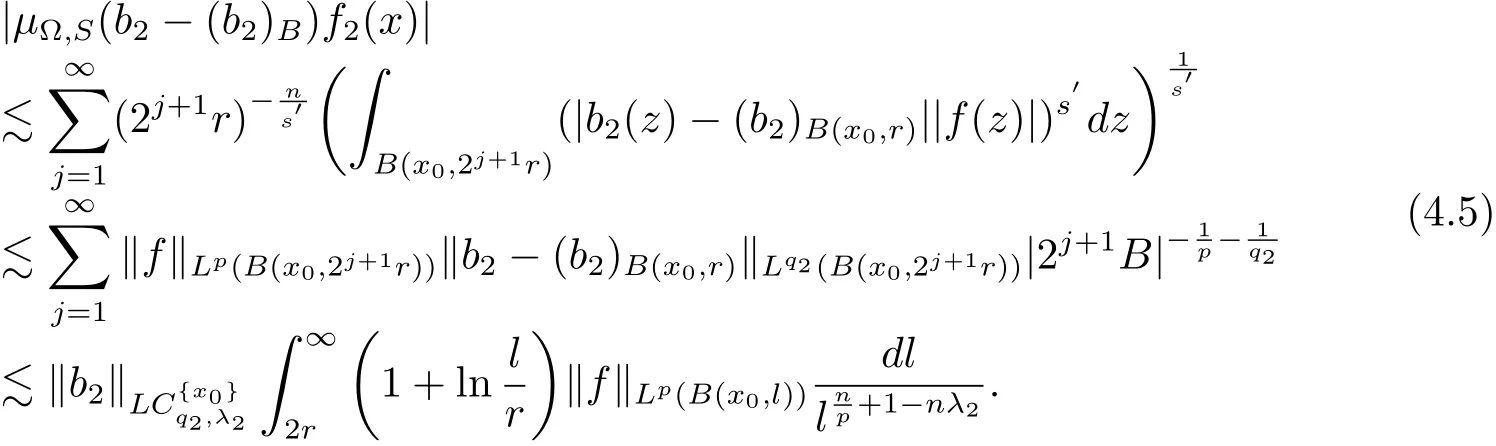
Let 1＜＜∞such thatthenand max{2,s′}＜＜ ∞.Thus,from H?lder’s inequality,(4.4)and(4.5),we obtain

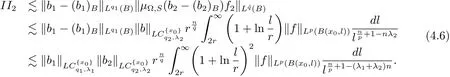
Similarly,

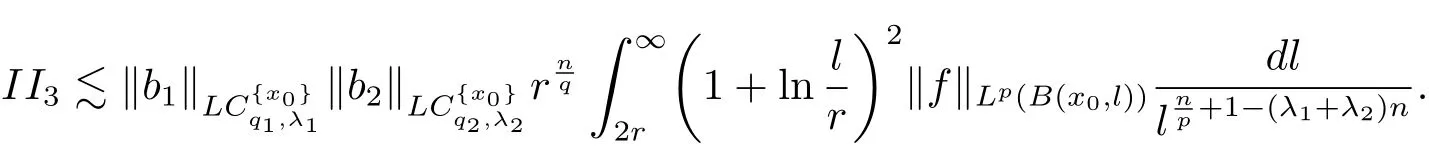
Let us estimate II4.It is analogue to the estimates of(4.4),(4.5)and(4.6),we have the following estimates.

When x∈ B,? ∈ L∞(Sn?1),we have

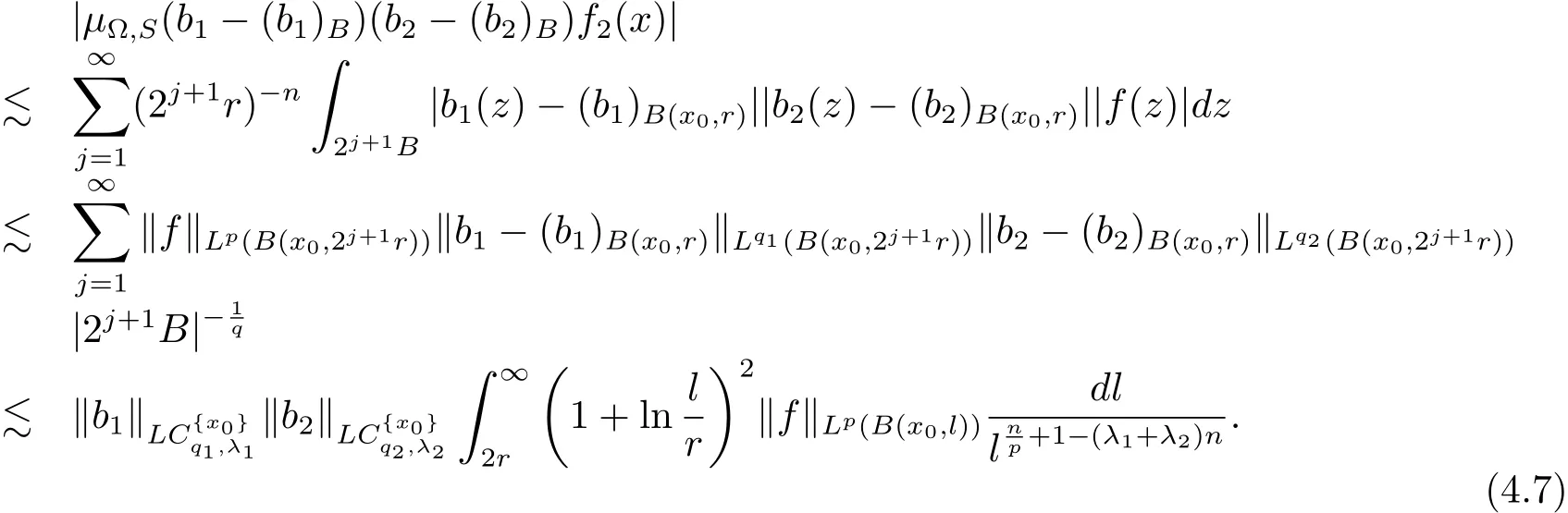
When x∈B,?∈Ls(Sn?1),1＜s＜∞,we have

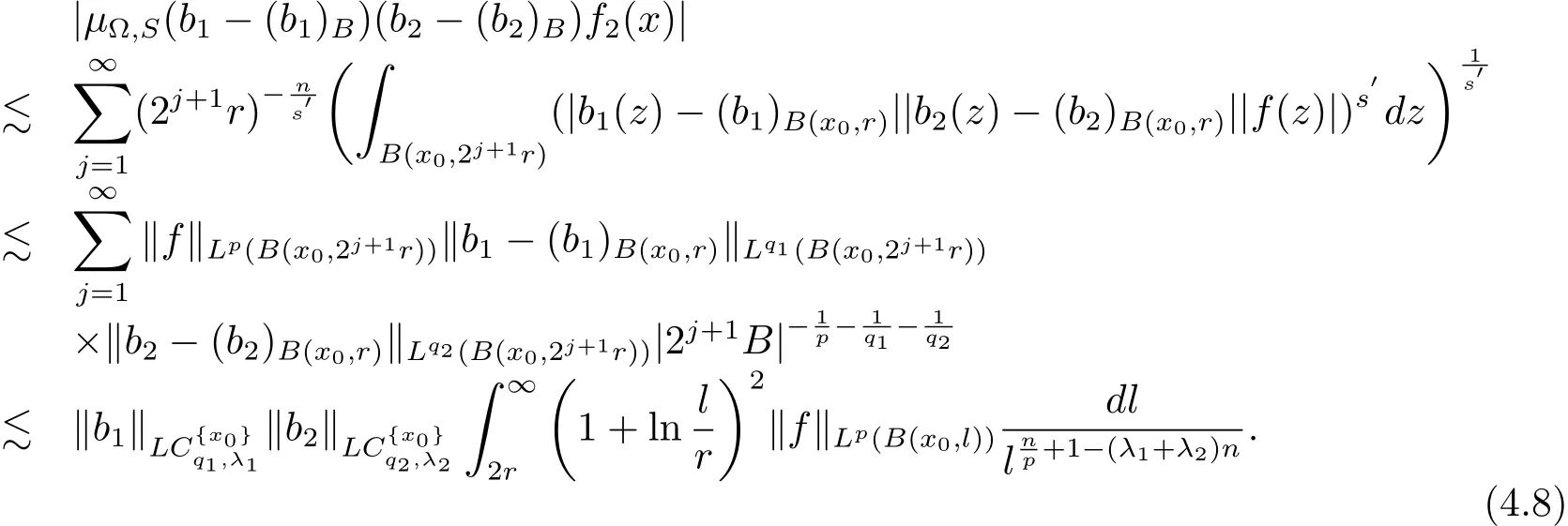
Therefore from(4.7)and(4.8),we have

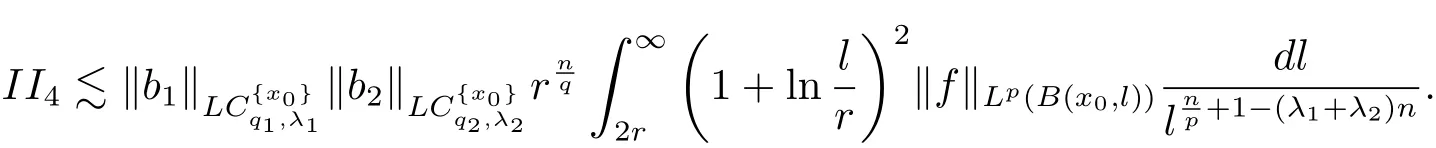
So from the estimates of II1,II2,II3and II4,it follows that

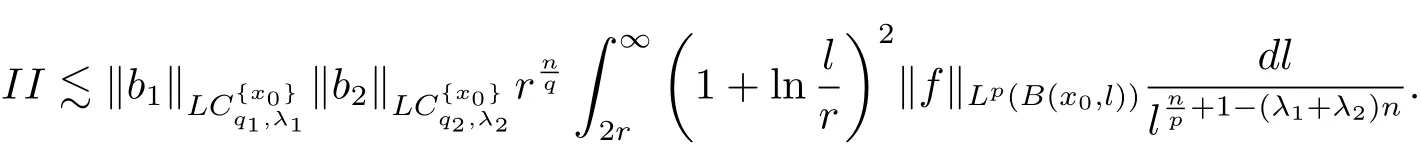
Therefore from the estimates of I and II,we deduced that

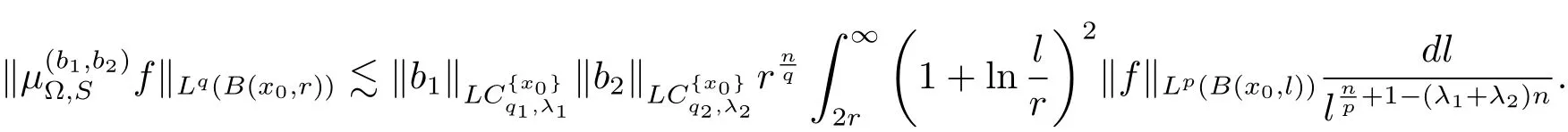
Thus the proof of Theorem 4.1 is completed.

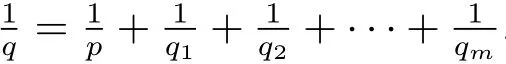
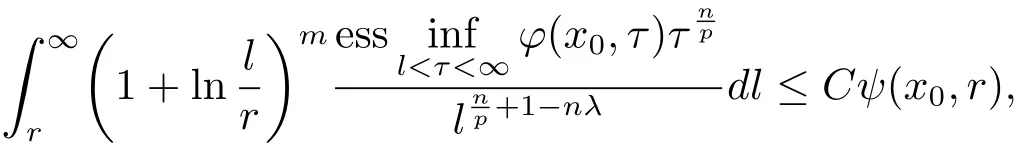
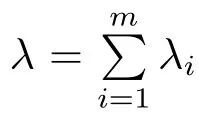
ProofTakingand.It is easy to see that

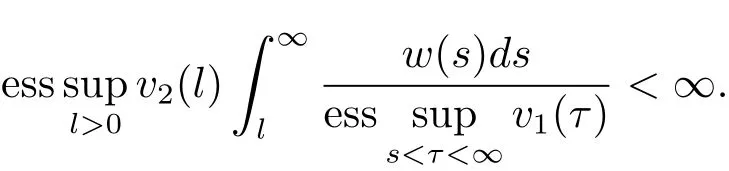
Thus by Lemma 2.2,we have

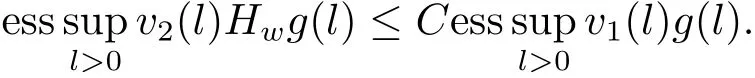
So

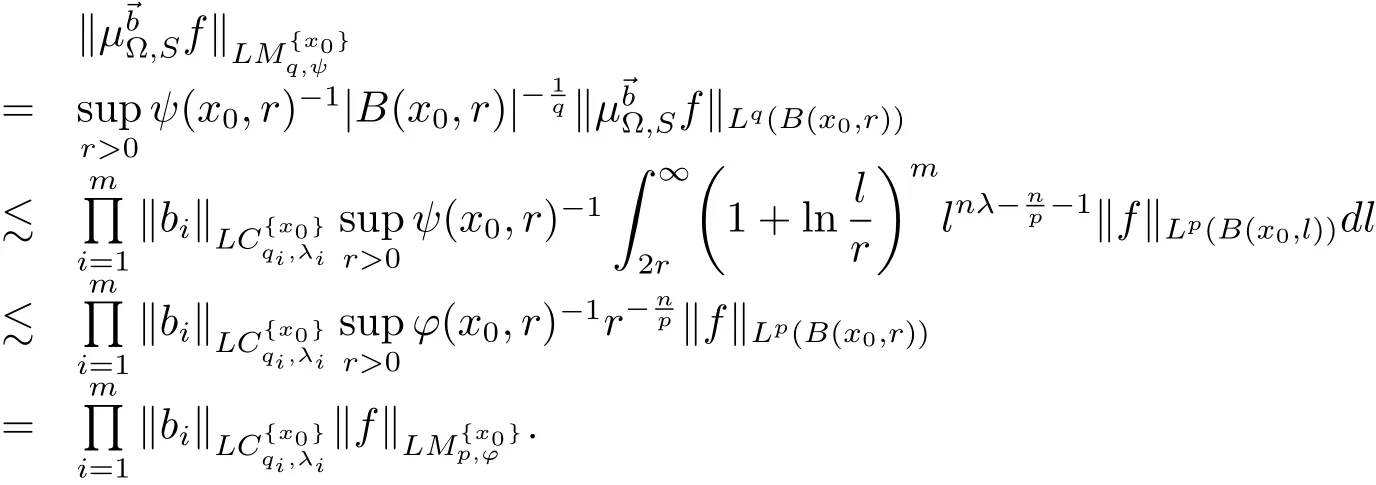
Thus the proof of Theorem 4.2 is finished.

References

[1]Chang S Y A,Wilson J M,Wolff T H.Some weighted norm inequalities concerning the Schr?dinger operators[J].Comment.Math.Helv.,1985,60(1):217–246.

[2]Ding Y,Fan D S,Pan Y B.Weighted boundedness for a class of rough Marcinkiewicz integrals[J].India Univ.Math.J.,1999,48(3):1037–1055.

[3]Tao S P,Wei X M.Boundeness of Littlewood-Paley operators with rough kernels on the weighted Morrey spaces[J].J.Lanzhou Univ.,2013,49(3):400–404.

[4]Lin Y,Liu Z G,Mao D L,Sun Z K.Parameterized Littlewood-Paley operators and area integrals on weak Hardy spaces[J].Acta.Math.Sin.,2013,29(10):1857–1870.

[5]Ding Y,Lu S Z,Yabuta K.On commutators of Marcinkiewicz integrals with rough kernel[J].J.Math.Anal.Appl.,2002,275(1):60–68.

[6]Ding Y,Xue Q Y.Endpoint estimates for commutators of a class of Littlewood-Paley operators[J].Hokkaido.Math.J.,2007,36(2):245–282.

[7]Chen Y P,Ding Y,Wang X X.Commutators of Littlewood-Paley operators on the generalized Morrey space[J].J.Inequal.Appl.,2010(1),Artical ID:961502,20 pages.

[8]Chen Y P,Wang H.Compactness for the commutator of the parameterized area integral in the Morrey space[J].Math.Inequal.Appl.,2015,18(4):1261–1273.

[9]Morrey C B.On the solutions of quasi-linear elliptic partial differential equations[J].Trans.Amer.Math.Soc.,1938,43(1):126–166.

[10]Balakishiyev A S,Guliyev V S,Gurbuz F,Serbetci A.Sublinear operators with rough kernel generated by Calder′on-Zygmund operators and their commutators on generalized local Morrey spaces[J].J.Inequ.Appl.,2015,2015(1):1–18.

[11]Guliyev V S.Local generalized Morrey spaces and singular integrals with rough kernel[J].Azerb.J.Math.,2013,3(2):79–94.

[12]Guliyev V S.Generalized local Morrey spaces and fractional integral operators with rough kernel[J].J.Math.Sci.,2013,193(2):211–227.

[13]Zhang L,Zheng Q.Boundedness of commutators for singular integral operators with oscillating kernels on weighted Morrey spaces[J].J.Math.,2014,34(4):684–690.