基于Pearson相關系數的快速虛擬網格匹配定位算法
郝德華,關維國,鄒林杰,焦 萌
(遼寧工業大學 電子與信息工程學院,遼寧 錦州 121001)
0 引言
全球定位系統[1]在室外環境可以精確定位,但在復雜的室內環境中定位效果并不理想,甚至無法定位,因此產生了多種基于無線信號(藍牙、WiFi等)的短距離室內定位技術。藍牙4.0容易部署、功耗低且大多智能設備都具有藍牙功能,所以基于藍牙4.0的室內定位技術備受學者推崇。而在室內定位方法的研究中,基于接收信號強度指示(Received Signal Strength Indicator, RSSI)的定位方法是最常用的方法之一,該方法因其不需額外添加硬件、低能耗、實現比較簡單等優點,成為定位技術的研究熱點[2]。基于RSSI的室內定位方法又主要分為基于RSSI測距的幾何定位算法和基于RSSI建庫的位置指紋定位算法[3]。
無線信號在復雜多變的室內環境中傳播易受墻壁、地板及行人等的阻擋而產生反射、折射及繞射影響[4],使各信標節點產生不同的信號衰減,從而影響定位精度。基于RSSI測距的定位算法利用理論或經驗傳播模型將RSSI轉成距離進行定位[5],但模型擬合和參數選擇會影響定位精度。如張鵬等[6]提出一種基于RSSI測距的高次消去最小二乘解算算法,但算法定位精度依賴于測距精確度且計算復雜度較高;基于RSSI建庫的位置指紋定位算法有較高的定位精度,如RADAR系統和Horus系統,均采用基于RSSI指紋建庫進行定位[7],然而,建立離線數據庫的工作量很大,室內定位環境復雜多變,在實際應用中存在很大的局限性。文獻[8]在離線階段構建RSSI位置指紋地圖,對實時接收的RSSI和指紋地圖中的RSSI值求其相關特性并據此定位,但需要建立離線指紋數據庫,離線階段建庫工作繁雜。王艷麗等[9]也提出了利用相關性匹配位置指紋庫的定位方法,定位精度較高,但同樣需要建立位置指紋庫,離線工作量很大。Wang等[10]提出了基于距離和RSSI之間相關性的網格定位算法(CORRelation, CORR),在非視距(Non Line Of Sight, NLOS)環境下利用該算法對路徑損耗指數進行實時修正,并根據幾何算法實現最終定位估計。
針對測距算法定位精度受模型影響較大以及位置指紋匹配定位算法離線建庫工作量大的缺點,本文在現有的利用相關性進行定位研究的基礎上,提出一種基于Pearson相關系數的快速虛擬網格匹配定位算法PCC(Pearson Correlation Coefficient)。利用Bounding-Box方法[11]依據信標節點ID(Identification)及通信半徑R確定初始虛擬網格劃分區域,并對其進行快速迭代細分;計算虛擬網格中心點到各信標節點距離的對數所構成向量L;依據接收信號強度Pr向量和L向量之間的Pearson相關系數在網格區域內遍歷尋優確定待定位節點的位置。為提高定位精度,選取Pearson相關系數接近于-1的k個近鄰坐標并以Pearson相關系數為權值加權最優估計待定位節點位置,從而使定位結果更加精確。最重要的是,本文算法無需離線指紋建庫,大大節省了定位工作量。
1 RSSI傳播特性分析
定位系統由待定位節點(藍牙終端設備)和多個iBeacon信標節點構成。終端設備在定位區域可收到各iBeacon信標節點發射的信息數據,包括通用唯一識別碼(Universally Unique Identifier, UUID)、Minor(識別區域內不同信標節點單號)、Major(識別不同區域的區域號)、RSSI、物理(Media Access Control, MAC)地址[9]。
在基于RSSI的定位過程中,待定位信標節點接收到各iBeacon信標節點的RSSI值和ID,計算出路徑損耗,然后利用損耗模型將其轉換成偽距估計值;但實際環境中,信號傳播會受到影響,使偽距估計值出現誤差并上下波動,從而影響定位精度。近年來室內定位主要的傳播路徑損耗模型有:自由空間傳播模型、Motley模型、華為路徑損耗模型、對數正態路徑損耗模型等[12],本文選用貼近于室內信號路徑損耗的華為模型并對其修正,其傳播損耗模型為:
PL=20 lg(f)+Nlg(d)+Pf(m)-28+Xσ
(1)
其中:PL表示信號傳播損耗值;f為信號的傳播頻率(MHz);N=10n,其中n為衰落因子,取值為2.5~3.0;Pf(m)為樓層穿透因子系數,在半開放室內環境下Pf(m)=6+3(m-1),在較為封閉的環境Pf(m)=15+4(m-1);同一樓層時m取值為1。參數經驗修正值為28 dBm;Xσ為高斯正態分布的隨機分布變量。
同一樓層空曠會議室視為半開放環境,測距利用華為室內路徑損耗修正模型,信標節點發射功率為Pt(dBm),根據式(1),可得在待定位節點處接收的RSSI參數Prssi為:
Prssi=Pt-PL=Pt-20 lg(f)-10nlg(d)-6+28-Xσ
(2)
對上式進行簡化,令:
A=Pt-20 lg(f)-6+28
(3)
則可得距離d與Prssi之間的相關特性如式(4)所示:
Prssi=A-10nlg(d)-Xσ
(4)
2 Pearson相關的快速虛擬網格定位
待定位節點接收各信標節點發送的ID和RSSI,算法首先對RSSI值進行預處理,以RSSI優化估計值參與最終定位估計。基于Pearson相關系數的快速虛擬網格定位利用遍歷尋優進行匹配定位,若定位區域較大,在整個定位區域進行虛擬網格劃分會造成迭代次數增加,定位時延增大。故本文先以Bounding-Box算法縮小并確定初始虛擬網格區域;然后再迭代細分虛擬網格,以虛擬中心到各信標節點距離的對數與RSSI求相關系數進行匹配定位。
2.1 RSSI信號預處理
實際測試中會發現無線信號在室內傳播時大部分RSSI值會在理論值附近上下波動,但總會有一小部分RSSI值會嚴重偏離理論值,直接對RSSI取平均參與定位可能會導致誤差較大,為了得到更精確的RSSI值,對信號進行預處理。
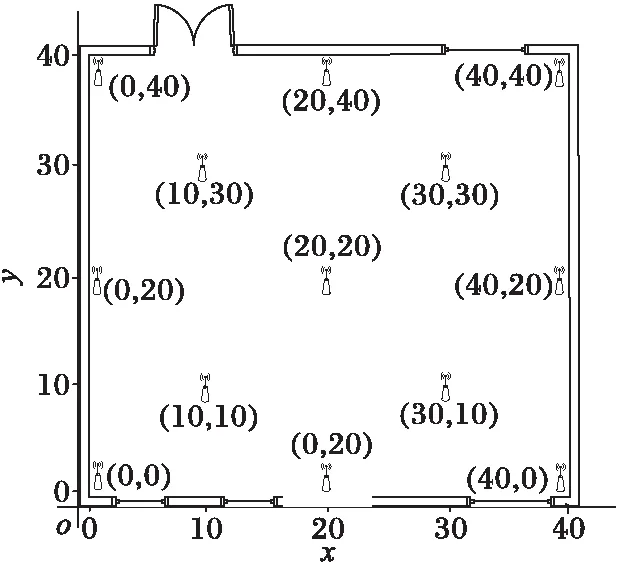
設在整個定位場景部署有Q個iBeacon信標節點,待定位節點可接收到M(M (5) 其中: (6) (7) 選擇RSSI高概率發生區即RSSI值出現概率較大的區域,經大量實驗分析選擇以σ規則設立置信區間,則臨界概率為0.68時最佳:0.68≤f(Pi)≤1。濾波后RSSI取值范圍為[μ-σ,μ+σ],對區間內的RSSI值進行計算,求其幾何平均值,即可得到最終參與定位的RSSI優化估計值。 為了減少算法計算量,提高基于Pearson相關系數的匹配定位算法速率。首先以Bounding-Box算法確定初始虛擬網格劃分區域,減小虛擬網格劃分區域。圖1所示為Bounding-Box方法示意圖,設待定位節點在iBeacon信標節點A、B、C的通信半徑范圍內,以各信標節點坐標為圓心,信標節點的通信距離為半徑畫圓,則各圓外接正方形得交疊區域為一個矩形(如圖中灰色部分),即定義此矩形區域為初始的虛擬網格劃分區域。 Bounding-Box核心思想是:在定位場景內待定位節點可以接收到M個iBeacon信標節點的ID、RSSI值以及通信半徑R,信標節點坐標為Xi=(xi,yi),其中i=1,2,…,M。依據信標節點的位置ID及通信半徑R,可得待定位節點所在的矩形區域,即為虛擬網格劃分區域,則該虛擬網格劃分區域的左下角坐標(xmin,ymin)和右上角坐標(xmax,ymax),由式(8)計算得: (8) 進而可得虛擬網格劃分區域可以表示為: (9) 依據上述Bounding-Box方法以鄰居信標節點的坐標確定虛擬網格劃分區域,待定位節點必定處于這個矩形區域中,從而可以在很大程度上縮小待定位節點可能存在的區域。以該區域再進行虛擬網格劃分,可大大減少定位算法的計算量,加快匹配定位速率,從而達到實時定位的效果。 圖1 Bounding-Box方法 Fig. 1 Bounding-Box method 在統計信號處理研究領域,相關性研究一直受到學者們的關注。對于相關性的研究即是利用相關的兩組變量來反映整體關聯性的方法[9,13]。Pearson相關系數又稱積矩相關,表示兩組變量的相關程度。其相關系數公式為: (10) 其中:X,Y表示兩組長度相等的向量,ρX,Y范圍為[-1,+1]。當值為0,兩組向量無關;當值在[-1,0),兩組向量負相關;當值在(0,+1],兩組變向量正相關。相關系數的絕對值越接近于1,表示相關程度越高。 (11) 在待定位節點所在區域,選取一個已知點,則可直接計算各鄰居iBeacon信標節點與該點之間的距離,計算所得距離值向量為D=[d1,d2,…,dM]。根據RSSI傳播模型分析可得Pr和D是相關的兩組向量,又根據式(4)可見,Prssi和lg(d)相關性更貼近于信號傳播模型規律,因此其相關性應比Prssi和d的相關程度更高,并且對數函數嚴格單調,lg(d)隨著d變化而單調變化,所以利用Prssi和lg(d)進行定位會有更準確的相關性體現,所以本文算法將距離d轉換成其對數的形式即: li=lg(di) (12) 則可得距離對數向量L=[l1,l2,…,lM],即可得到關于已知位置點到各iBeacon信標節點的距離對數矩陣: (13) 若在定位區域內選取多個已知點,則基于Pearson相關系數的定位估算方法即分別計算定位區域內選取的各已知節點與各信標節點之間的Pr向量和L向量之間的相關程度。根據式(4)表現出的相關特性可以看出,Pr向量和L向量呈負相關特性。兩向量負相關性越高,則已知點越接近于待定位節點,其計算公式可由式(10)推導出: (14) 若是假設的已知點就是待定位節點,在無噪聲環境下,其Pearson相關系數值越接近于-1(甚至等于-1),定位點越接近于待定位節點,定位精度越高,從而完成定位估計。 1)在整個定位區域部署Q個iBeacon信標節點,每次選取M個參與定位(M 2)利用Bounding-Box算法根據ID及通信半徑R確定并縮小虛擬網格劃分區域,取該矩形區域最小邊長的1/4作為初始虛擬網格的邊長。每次迭代細分可以得到T個虛擬網格,各個虛擬網格中心的坐標為Xi,t=(xi,t,yi,t),其中t=1,2,…,T;i=0,1,2,…。i為快速迭代次數。 3)求解各虛擬網格中心到待定位點的距離對數向量Lit=[li1,li2,…,liM]。對Pr向量和Lit向量分別求解Pearson相關系數ρ并從小到大進行排序可得集合ρi={ρi,1,ρi,2,…,ρi,t,…,ρi,T}。 5)更新網格邊長mi+1=mi/2。在噪聲條件下虛擬網格迭代劃分時會出現不規則區域,若直接以不規則區域外接矩形進行下一次迭代會造成計算重復而增加計算量。故本文迭代算法直接對虛擬網格中心坐標進行迭代細分,則第i+1次虛擬網格劃分所得的網格中心坐標為: (15) 6)判斷虛擬網格邊長是否小于設定邊長閾值。若小于則轉入7)輸出結果,否則轉到步驟3)循環。 7)通過Pearson相關系數加權得到坐標估計值為: (16) 為分析本文PCC算法性能,定位仿真實驗環境選取一個長寬為40 m×40 m會議室環境。整個定位區域均勻部署13個iBeacon信標節點,iBeacon信標的廣播發射功率均設置為0 dBm;具體信標布置場景如圖2所示。 圖2 室內定位仿真環境 Fig. 2 Indoor localization simulation environment 本文iBeacon信標節點通信半徑均為25 m;在定位階段終端設備對個信標節點均采集10次。在空曠的會議室環境中,經實驗采集驗證,路徑損耗指數擬合值為2.6,定位噪聲Xσ基本服從0均值、標準差為3 dBm的高斯噪聲。 本文PCC算法中網格迭代劃分依據和虛擬網格邊長的更新速度共同影響算法的定位精度與定位效率,為選取合適的迭代參數,在不同迭代參量條件下對算法進行定位仿真實驗可得結果如表1所示,可以看出以二分法(size(ρi)/2)為劃分依據且以mi+1=mi/2進行網格邊長更新時,定位時間最長且定位效果較差;而以四分法(size(ρi)/4)為劃分依據且以mi+1=mi/4進行網格邊長更新時,定位時間最短但定位誤差較大。故綜合表1數據,本文選取四分法(size(ρi)/4)為劃分依據并以mi+1=mi/2進行網格邊長更新。 表1 不同迭代條件下PCC算法性能對比Tab. 1 Performance comparison of PCC algorithm under different iteration conditions 虛擬網格劃分邊長閾值是PCC算法一個重要參數,理論上邊長閾值越小,算法定位精度越高,但在噪聲條件下,網格細分到某一閾值后將無法繼續提高定位精度,反而增加定位計算量。為選定合適邊長閾值,本文針對不同噪聲條件對算法進行定位仿真分析,算法定位誤差隨邊長閾值變化情況如圖3所示。低噪情況下,定位精度隨邊長閾值減小而提高;在標準差為2~5 dBm的顯著噪聲條件下,當邊長閾值小于1時,算法定位誤差趨于平緩,定位精度不在隨邊長閾值減小提高,因此本文將邊長閾值選定為1 m。 圖3 定位誤差隨邊長閾值變化 Fig. 3 Positioning error changes with length threshold 在典型室內環境下(RSSI噪聲σr=3 dBm),將本文PCC算法與消去高次加權最小二乘法、CORR、相關性匹配定位算法進行定位仿真對比,本文算法以3.2節選定為參數進行定位仿真實驗,可得定位性能對比如表2所示。本文算法的定位誤差小于2 m的累計分布函數(Cumulative Distribution Function, CDF)概率為94.2%,其定位均方根誤差(Root-Mean-Square Error, RMSE)為1.202 m,比消去高次加權最小二乘法、CORR、相關性匹配定位算法分別提高0.283 m、0.397 m和0.150 m。定位精度優于其他三種算法;雖然定位精度比相關性匹配定位算法僅提高了0.150 m,但無需建立數據庫,大大減少了采集工作量,降低了定位成本,更容易應用推廣。另外根據表2中定位最大定位誤差值和最小定位誤差值可見,PCC算法比其他算法定位穩定性較高。 表2 不同定位算法性能對比Tab. 2 Performance comparison of different localization algorithms RSSI噪聲標準差的大小會影響信標節點的定位精度。為測試本文PCC算法的抗噪性能,在噪聲標準差從1 dBm變化到8 dBm的條件下,選取500個隨機位置點對各算法進行定位仿真實驗,各算法均方根誤差隨噪聲標準差變化情況如圖4所示,可見不同噪聲標準差下PCC算法的定位均方根誤差小于其他算法。當σr=2 dBm時,PCC算法、CORR、相關性匹配定位算法和消去高次加權最小二乘法定位均方根誤差分別為0.918 m、1.510 m、1.030 m和0.923 m。在σr=7 dBm的惡劣環境下,PCC算法的均方根誤差可保持為2.592 m;CORR的均方根誤差為2.769 m;相關性匹配定位算法的均方根誤差為2.894 m;而消去高次加權最小二乘法的均方根誤差則為3.484 m。可見本文PCC算法相對于其他算法具有更好的抗噪性能。 圖4 不同噪聲下各算法定位均方根誤差對比 Fig. 4 Comparison of positioning RMSE of each algorithm under different noises 在RSSI噪聲標準差分別為2~5 dBm變化條件下,對本文PCC算法進行500次蒙特卡羅定位實驗。定位誤差累積分布函數CDF曲線如圖5所示。當噪聲標準差σr=2 dBm時,定位精度優于2 m的概率可達到98.7%;當噪聲標準差σr=4 dBm,定位精度在86.6%概率下優于2 m;在噪聲標準差σr=5 dBm的惡劣環境下,定位精度仍可保證在75.6%概率下優于2 m。所以PCC算法有較高的定位精度和良好的魯棒性。 為驗證本文PCC算法的環境適用性能,仿真環境二選取一長寬為30 m×3 m的室內走廊,在該環境中均勻部署6個iBeacon信標節點,由于環境寬度限制,網格劃分邊長閾值設置為0.5 m,其余參數設置均與3.1節仿真環境相同,考慮信號的反射、折射等多徑影響以及行人的遮擋,走廊環境實測統計后噪聲標準差約為3 dBm。在定位區域內隨機選取300個待定位節點求定位誤差,可得其定位估計誤差如圖6所示,PCC算法的平均定位估計誤差為1.141 m。 圖5 定位誤差的累積概率分布 Fig. 5 Cumulative probability distribution of positioning error 圖6 定位估計誤差 Fig. 6 Positioning estimation error 室內定位測試實驗選取學校教三樓二樓走廊環境,長寬為20 m×2.4 m,測試環境如圖7(a)所示。在兩側墻壁上均勻部署6個尋息科技S1U型信標節點,信標天線高度2.3 m,使用紅米手機為接收設備采集信號進行定位,信號采集App界面如圖7(b)所示。 圖7 室內定位測試 Fig. 7 Indoor positioning test 在測試環境中選取5個定位點進行測試分析,在固定位置使用紅米手機連續接收6個信標節點的信號強度,每個位置點對各信標節點均采樣10次,采樣間隔為500 ms。測試得接收信號強度和定位結果如表3所示,可見實際測試定位誤差與圖6仿真的平均定位誤差基本一致,故本文PCC算法在實際定位中也可達到相同的定位效果。 表3 待測位置點的測試定位誤差Tab. 3 Test positioning error of points to be measured 本文針對位置指紋匹配定位算法離線采集建庫工作量大的缺點,提出一種基于Pearson相關系數的快速虛擬網格匹配定位算法。算法計算RSSI向量與各虛擬網格中心點到各信標節點的距離對數向量之間的Pearson相關系數,并據此進行匹配定位估計;同時采用Bounding-Box方法確定初始虛擬網格區域,并以快速迭代的形式進行網格細分,從而保證了定位算法的計算效率,以達到實時定位的效果。通過仿真及實驗表明,本文算法不僅具有優于位置指紋匹配定位算法、CORR算法和消去高次加權最小二乘算法的定位精度和穩定性,更重要的是,虛擬網格無需建庫采集指紋,克服了位置指紋匹配定位算法因建立離線指紋庫工作量大而難以推廣應用的缺點,同時比CORR算法的定位速率更高,能夠滿足室內實時定位的需求。在后續的研究工作中,將開展該算法在動態環境下連續定位估計問題的研究。 參考文獻(References) [1] MANNUCCI A J, WILSON B D, YUAN D N, et al. A global mapping technique for GPS-derived ionospheric total electron content measurements [J]. Radio Science, 2016, 33(3): 565-582. [2] DENG Z, YU Y, YUAN X, et al. Situation and development tendency of indoor positioning [J]. China Communications, 2013, 10(3): 42-55. [3] 樂志偉,王浩,謝小軍.基于RSSI障礙勢能矯正的定位算法[J].電子測量與儀器學報,2017,31(2):200-207.(LE Z W, WANG H, XIE X J. Localization algorithm based on RSSI obstacles potential energy correction [J]. Journal of Electronic Measurement and Instrumentation, 2012, 9(2): 52-65.) [4] 畢京學,甄杰,郭英.室內定位無線接收信號強度測距模型的研究[J].導航定位學報,2014,2 (4):8-10. (BI J X, ZHEN J, GUO Y. Indoor positioning range based model of the received signal strength [J]. Journal of Navigation and Positioning, 2014, 2(4): 8-10.) [5] 周艷.基于RSSI測距的傳感器網絡定位算法研究[J].計算機科學,2009,36(4):119-120.(ZHOU Y. Study of wireless sensor network localization algorithm based on RSSI [J]. Computer Science, 2009, 36(4): 119-120.) [6] 張鵬,周建國,馮欣,等.接收信號強度測距法無線室內定位解算方法研究[J].測繪科學,2014,39(4):13-16.(ZHANG P, ZHOU J G, FENG X, et al. RSSI ranging based wireless indoor positioning solutions [J]. Science of Surveying and Mapping, 2014, 39(4): 13-16.) [7] 關維國,魯寶春.基于二維網格融合特征參數的室內匹配定位算法[J].計算機應用,2014,34(9):2464-2467.(GUAN W G, LU B C. Indoor matching localization algorithm based on two-dimensional grid characteristic parameter fusion [J]. Journal of Computer Applications, 2014, 34(9): 2464-2467.) [8] SUN Y L, XU Y B. Error estimation method for matrix correlation-based Wi-Fi indoor localization [J]. Ksii Transactions on Internet & Information Systems, 2013, 7(11): 2657-2675. [9] 王艷麗,楊如民,余成波,等.相關性匹配藍牙信標位置指紋庫的室內定位[J].電訊技術,2017,57(2):145-150.(WANG Y L, YANG R M, YU C B, et al. Indoor localization of bluetooth beacon position fingerprint based on correlation algorithm [J]. Telecommunication Engineering, 2017, 57(2): 145-150.) [10] WANG R, FENG J. Grid-based correlation localization method in mixed line-of-sight/non-line-of-sight environments [J]. Ksii Transactions on Internet & Information Systems, 2015, 9(1): 87-107. [11] 張乙竹,李雅晴,周禮爭,等.基于自適應RSSI的Bounding-Box輪回選擇WSN定位算法[J].計算機應用究,2016,33(9):2767-2768.(ZHANG Y Z, LI Y Q, ZHOU L Z, et al. Bounding-box recurrent selection algorithm for WSN based on self-adapted RSSI [J]. Application Research of Computers, 2016, 33(9): 2767-2768.) [12] 劉云,劉菁原.基于RSSI的加權質心定位算法優化研究[J]. 華中師范大學學報(自然科學版),2016,50(3):358-362.(LIU Y, LIU J Y. Optimization research on weighted centroid localization algorithm based on RSSI [J]. Journal of Huazhong Normal University (Natural Sciences), 2016, 50(3): 358-362.) [13] 胡暉,許浩峰,包偉華.基于相關性算法的超聲波回波定位[J].自動化儀表,2015,36(10):96-98.(HU H, XU H F, BAO W H. Ultrasonic echo location based on correlation algorithm [J]. Process Automation Instrumentation, 2015, 36(10): 96-98.) This work is partially supported by the Directional Program of Liaoning Province Natural Science Foundation (20170540437). HAODehua, born in 1992, M. S. candidate. His research interests include mobile communication and wireless technology. GUANWeiguo, born in 1973, Ph. D., professor. His research interests include mobile network positioning, ubiquitous network wireless positioning. ZOULinjie, born in 1991, M. S. candidate. Her research interests include mobile communication and wireless technology. JIAOMeng, born in 1990, M. S. candidate. Her research interests include communication technology and application engineering.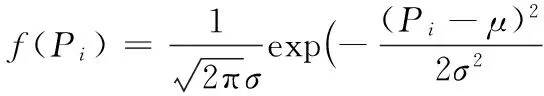
2.2 Bounding-Box確定虛擬網格劃分區域

2.3 基于Pearson相關的定位估算方法


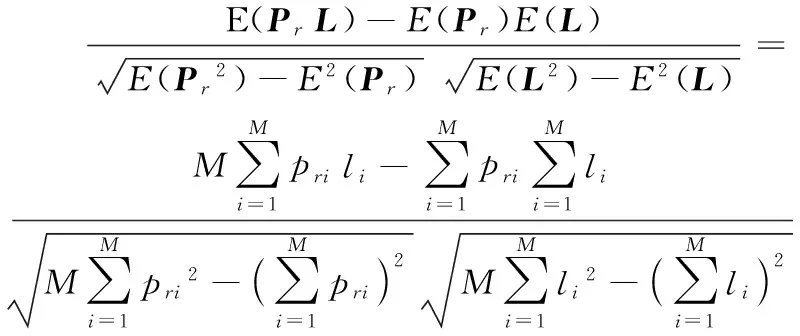
2.4 PCC定位算法步驟

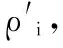
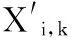


3 仿真及實驗分析
3.1 仿真環境
3.2 算法參數的優選仿真分析


3.3 定位算法性能仿真分析




3.4 實際測試實驗分析


4 結語

