三角波強加載下延性金屬多次層裂破壞問題*

張鳳國,劉 軍,王 裴,2,胡曉棉,2,周洪強,邵建立,馮其京

(1.北京應用物理與計算數學研究所，北京 100094;2.北京應用物理與計算數學研究所計算物理重點實驗室,北京 100088)

在爆轟或超高速撞擊等強載荷作用下，沖擊波在靶板自由面反射形成卸載拉伸波，并導致在靠近靶板自由面附近區域產生層裂(或多次層裂)損傷破壞，該問題涉及到武器物理的內爆過程、超高速撞擊下的空間防護以及國防兵器中的飛片破甲和重要民用設施的防爆等不同領域，因而該問題的研究具有重要的應用背景[1-3]。目前的多次層裂研究主要包括固體多次層裂以及熔化金屬的拉伸破壞兩類：當材料的熔點較高(如金和鋁等)或加載強度較低時，材料呈現固體多次層裂情況，采用網格分離技術，數值模擬可以清晰地展示多次層裂的物理現象；熔點較低的金屬材料(如錫和鉛等)在強沖擊加載下，材料將呈現卸載熔化破碎現象(自由表面形成為一密實薄層，在薄層與密實基體之間為材料熔化破碎區域)，該問題涉及到材料的壓縮、拉伸、相變、損傷演化直至破碎的復雜物理過程，而其損傷演化過程包括孔洞成核、增長、匯合以及材料網狀化失穩直至破碎，因而問題的研究相對困難很多，同時，因材料熔化破碎的顆粒尺寸相對很小，這又為實驗和數值模擬提出了更高要求，精細化理論分析難度較大[4-6]。

當前對多次層裂的研究主要以實驗和相應的數值模擬為主。近幾年隨著實驗技術的發展，飛片加載、爆轟加載以及激光加載方法已經應用于材料多次層裂問題的研究，同時，通過采用Asay窗、壓電石英計(壓電探針)、VISAR測速以及質子照相等實驗手段可以獲得微噴物質質量和密度-速度分布信息、自由面速度變化歷史以及材料破壞的宏觀物理表象，多物理實驗結果的解讀以及精細化數值模擬結果的分析使得人們對多次層裂物理機理的認識不斷加深[7-9]。不過，因該問題涉及的物理機理比較復雜，理論研究難度很大，特別是熔化金屬的拉伸破壞研究。實際研究中主要關注的是材料的破壞深度所引起的工程防護問題以及材料破碎顆粒的尺度和速度的分布對結構內部設施造成的二次破壞等問題，因強加載下材料的破壞程度很大，實驗樣品不易回收，需要結合理論、實驗和數值模擬對問題進行綜合分析。本文中，針對沒有升壓的簡單三角形卸載稀疏波引起的材料固體多次層裂問題，采用應力瞬時判據以及損傷累積Tuler-Butcher判據[10]，解析不同的損傷模型、加載條件等因素對層裂片厚度和靶板多次層裂破壞深度的影響。

1 靶板的受力

針對爆轟、超高速撞擊或激光加載下材料內部產生的三角形沖擊波C(沖擊波到達自由面時的強度為σm，波長為λ，波速為c)，不失一般性，本文中考慮沒有升壓情況下的三角形沖擊波，且假設自由面反射的卸載拉伸波R的強度不變，同時，忽略沖擊加載導致材料壓縮損傷的影響，則靠近自由面靶板內部的受力見圖1。

沖擊波到達自由面后再傳播t時刻后，距自由面d處(d≤ct)靶板內部的沖擊波壓力為σm(λ-d-ct)/λ,卸載拉伸波強度為-σm(λ+d-ct)/λ，則d處靶板內部受力為：

(1)

由式(1)可知：自由面附近靶板內部的拉伸應力與時間無關，只與距離有關，并隨距自由面距離的增大而線性增大，同時，其拉伸應力與沖擊波強度成正比、與沖擊波波長成反比[11-12]。

2 靶板的損傷與破壞

沖擊載荷作用下靶板的層裂破壞問題研究具有很好的應用背景，因此該問題的研究得到持續關注，從早期的瞬時斷裂判據(最大拉應力或應變)、損傷累積判據到近期耦合材料微細觀信息的損傷累積判據，其研究進展使得人們對材料破壞微細觀機理的認識不斷深入[13-14]。不過，損傷模型的發展，一方面可以對損傷演化過程進行更加精細化的物理描述，另一方面，卻為一些工程問題定性的理論分析帶來了不方便。這里采用目前針對一些工程問題，特別是強沖擊下的損傷破壞問題，部分商用程序還在采用的應力瞬時斷裂判據和Tuler-Butcher損傷累積判據，分析不同因素對三角波強加載下延性金屬多次層裂破壞的影響。

2.1 應力瞬時斷裂判據

當靶板內部拉伸應力σd高于材料的最大抗拉強度σcr時，材料發生斷裂。由式(1)可知，靶板斷裂后產生的層裂片厚度為：

(2)

(3)

即層裂片的厚度不變，總的層裂片的個數為N=AINT(σm/σcr)，從而靶板的破壞深度為：

(4)

2.2 Tuler-Butcher損傷累積判據

Tuler-Butcher 累積損傷破壞準則目前仍被廣泛地應用于描述金屬、巖石和混凝土等材料的動態剝離斷裂問題。它的表達式為：

(5)

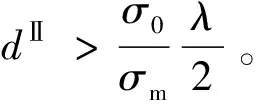
(6)

(7)

求解此方程有：

(8)

(9)

對應的層裂片厚度為：

(10)

以及拉伸波強度為：

(11)

(12)

即層裂片的厚度不變。總的層裂片的個數為N=AINT(σm/σf)，從而靶板的破壞深度為：

(13)

3 不同因素影響的分析

以純鋁材料為例來分析不同因素對三角波強加載下延性金屬微層裂破壞的影響。實驗[15]中鋁靶厚100 μm，加載激光能量為0.72×1011W/cm2，強度約為9.64 GPa，脈沖寬度3.9 ns；當沖擊波達到自由面時其沖擊波強度σm約為4.5 GPa，波長λ約為58 μm；實驗中層裂片厚度約為28 μm。純鋁材料中的沖擊波傳播速度c=5 386 m/s，損傷開始增長的臨界應力σ0=1.0 GPa[3]。由公式(2)可以得模型參數σcr=4.345 GPa；同時，對于同一物理問題，材料的斷裂位置相同，則根據公式(10)，進一步可以得模型參數K=13.388 Pa·s。

首先，取參數α=λ/σm，圖2顯示了2個模型計算的層裂片厚度與α之間的關系：隨著α值的提高，即沖擊波波長λ的增大和強度σm的減弱，層裂片厚度逐漸增大，因短脈沖沖擊波在靶板內部傳播過程中強度減弱、波長展寬，因此，圖2進一步展示了層裂片厚度隨靶板厚度增大而增大的物理機理[3]；同時，相對于應力瞬時斷裂判據，隨著α值的提高，沖擊波波形上升的斜率減小，則損傷累積判據中損傷累積時間的影響增強，因而采用損傷累積判據計算的層裂片厚度偏小，且兩者間的差距隨α值的提高而增大，反之，隨著α值的減小，應力的影響占主導因素，但因損傷累積時間影響的存在，采用損傷累積判據計算的層裂片厚度偏大，不過，對于極端強加載下(α值趨于0)，2個模型計算的層裂片厚度均趨于0。

其次，基于目前工程中仍常用的Tuler-Butcher 累積損傷破壞準則，圖3進一步顯示了層裂片厚度變化與加載強度σm、加載波形的波長λ之間的關系：隨著加載波形波長減小，層裂片厚度隨之減小，且減小幅度呈逐漸加快的趨勢(圖3(a))；而加載強度與層裂片厚度之間為近似反比例關系，即隨著加載強度提高，層裂片厚度迅速減小(圖3(b))。綜合圖2～3的計算結果，影響層裂片厚度的關鍵因素是沖擊波的加載強度和波長以及材料本身的物理性質，而層裂片厚度與強加載下工程問題中所感興趣的材料破碎顆粒尺寸直接相關，因此，分析材料的微層裂破碎問題時應重點關注沖擊波的強度和波長。

最后，雖然層裂片厚度隨加載強度的提高和沖擊波波長的減小而減小，但基于公式(4)和(13)分析可知，材料的破壞深度小于沖擊波波長的一半，特別是對于極端加載下，我們發現一個很有意義的事情，即加載條件(λ、σm)和材料性質(σ0或σcr)在公式中可以近似約去，則材料因卸載拉伸引起的破壞深度近似為沖擊波波長的一半，且該結論與材料性質和加載條件無關，這一點對于超高速撞擊的空間防護以及內爆等工程問題中的材料損傷破壞分析非常重要。為此，進一步對此進行數值驗證，圖4為0.5 mm厚錫靶在0.05 mm厚錫飛片以5 km/s高速撞擊下損傷破壞的數值模擬結果：圖4(a)為沖擊波剛到達靶內的波形；圖4(b)為沖擊波到達靶自由面的波形，可知，沖擊波的寬度約為220 μm；圖4(c)為錫靶最后破壞的數值模擬結果，靶板的破壞深度約為110 μm，從而數值驗證了強沖擊下破壞深度約為沖擊波波長的一半這一結論。同時，Chen等[16]進行的鉛靶多次層裂實驗研究表明：加載速率和峰值壓力對多次層裂碎片的密度-速度曲線有重要影響，而對多次層裂顆粒的總質量的影響可以忽略不計，因多次層裂碎片的密度-速度曲線與層裂片的厚度相關，而多次層裂顆粒的總質量即為靶板的破壞深度，因此，本文中的分析結果也與其實驗分析結果定性一致。

不過，本文中只是針對沒有升壓的簡單的三角形波形進行了討論，波形改變對于層裂片厚度的影響可以基于以上思路進行討論。同時，圖2顯示了不同模型的計算結果差別可能較大，因此，采用層裂損傷模型分析微層裂問題時需要較寬范圍內的多個實驗點對模型及其參數進行驗證和標定。

4 結 語

基于經典的應力瞬時斷裂判據和目前工程中仍常用的Tuler-Butcher 累積損傷破壞準則，對三角形沖擊波強加載條件下的材料多次層裂問題進行了討論。對于工程中所關注的與材料破碎顆粒尺度直接相關的層裂片厚度以及材料因卸載拉伸引起的破壞深度，分析結果顯示：層裂片的厚度隨著三角形沖擊波的升壓角度(即σm/λ)的提高而減小；材料的破壞深度小于沖擊波波長的一半，在強沖擊加載條件下，破壞深度約為沖擊波波長的一半；材料本身的物理性質和加載條件主要影響層裂片厚度，而對于強加載下破壞深度的影響很小。

參考文獻：

[1] 陳華燕,曾祥國,朱文吉,等.爆炸荷載作用下橋梁動態響應及其損毀過程的數值模擬[J].四川大學學報(工程科學版),2011,43(6):15-19.

CHEN Huayan, ZENG Xiangguo, ZHU Wenji, et al. Numerical simulation of dynamic response and damage process for bridge under blast loading[J]. Journal of Sichuan University (Engineering Science Edition), 2011,43(6):15-19.

[2] 李建光,張鑫.工程層裂準則簡要回顧[J].哈爾濱理工大學學報,2012,17(6):86-91.

LI Jianguang, ZHANG Xin. Brief review of the spallation criterion of engineering[J]. Journal of Harbin University of Science and Technology, 2012,17(6):86-91.

[3] ZHU W H, YOSHIDA M, TANIMURA S. Tensile fracture in Al foils acted by laser pulses[C]∥Proceedings of the International Symposium on Plasticity and Impact (ISPI2001), Engineering Plasticity and Impact Dynamics. Zhuhai, China: World Scientific Publishing Co. Pte. Ltd., 2001:279-293.

[4] LESCOUTE E, RESSéGUIER T, CHEVALIER J M, et al. Ejection of spalled layers from laser shock-loaded metals[J]. Journal of Applied Physics, 2010,108(9):093510.

[5] HOLTKAMP D B, CLARK D A, FERM E N, et al. A survey of high explosive-induced damage and spall in selected metals using proton radiography[C]∥Shock Compression of Condensed Matter. Portland, Oregon, 2003:507-510.

[6] 陳永濤,任國武,湯鐵鋼,等.爆轟加載下金屬樣品的熔化破碎現象診斷[J].物理學報,2013,62(11):116202.

CHEN Yongtao, REN Guowu, TANG Tiegang, et al. Experimental diagnostic of melting fragments under explosive loading[J]. Acta Physica Sinica, 2013,62(11):116202.

[7] JARMAKANI H, MADDOX B, WEI C T, et al. Laser shock-induced spalling and fragmentation in vanadium[J]. Acta Materialia, 2010,58:4604-4628.

[8] 陳永濤,洪仁楷,陳浩玉,等.熔化狀態下金屬樣品表面的微噴射問題[J].物理學報,2016,65(2):026201.

CHEN Yongtao, HONG Renkai, CHEN Haoyu, et al. Experimental investigation of ejecta on melted Sn sample under shock loading[J]. Acta Physica Sinica, 2016,65(2):026201.

[9] ZHANG Lin, LI Yinghua, LI Xuemei, et al. Exploration of the fragmentation of laser shock-melted aluminum using X-ray backlighting[J]. Aip Advances, 2016,6(5):013506.

[10] TULER F R, BUTCHER B M．A criterion for the time dependence of dynamic fracture[J]. International Journal of Fracture Mechanics, 1968,4(4):431-440．

[11] JOHNSON J N, GRAY G T, BOURNE N K. Effect of pulse duration and strain rate on incipient spall fracture in copper[J]. Journal of Applied Physics, 1999,86(9):4892-4901.

[12] MOSHE E, ELIEZER S, DEKEL E, et al. An increase of the spall strength in aluminum, copper, and Metglas at strain rates larger than 107s-1[J]. Journal of Applied Physics, 1998,83(8):4004-4011.

[13] JACQUES N, MERCIER S, MOLINARI A. Effects of microscale inertiaon dynamic ductile crack growth[J]. Journal of the Mechanics and Physics of Solids, 2012,60:665-690.

[14] 張鳳國,周洪強.晶粒尺度對延性金屬材料層裂損傷的影響[J].物理學報,2013,62(16):164601.

ZHANG Fengguo, ZHOU Hongqiang. Effects of grain size on the dynamic tensile damage of ductile polycrystalline metal[J]. Acta Physica Sinica, 2013,62(16):164601.

[15] SHALOM E, IRITH G, TUVIA B N. Laser-induced spall in metals: Experiment and simulation[J]. Journal of Applied Physics, 1990,67(2):715-724.

[16] CHEN Y, HU H, TANG T, et al. Experimental study of ejecta from shock melted lead[J]. Journal of Applied Physics, 2012,111(5):053509.