基于Cowper-Symonds方程的相似理論修正方法*

蘇子星，何繼業

(1.西北工業大學航空學院，陜西 西安 710072；2.西北工業大學航天學院，陜西 西安 710072)

相似理論是實驗設計中較為熱門的研究問題[1]，其核心在于確定外載條件相似系數、以使模型與全尺寸原型實驗結果接近。經典相似理論[2]成熟、有效，已在(準)靜態實驗中廣為應用；然而近年來，具備高速、高應力、高應變率等特點的動態實驗(如沖擊實驗等)逐漸成為研究重點。由于動態實驗中的特征參數存在非線性特點，若繼續使用經典相似理論作為指導，則會給實驗結果帶來較大誤差。因此，有必要對經典相似理論進行修正。

針對沖擊實驗，談慶明[3-4]曾就沖擊相似律進行過詳細的分析和討論。Calladine等[5]提出通過改變外載條件來抵消應變率效應影響，并給出了修正方法。Oshiro等[6]經過嚴格的數學推導，進一步修正了基于經驗的Calladine相似理論。

本文中在已有研究基礎上，引入Cowper-Symonds方程來考慮材料本構中應變率效應影響、并重新推導外載條件相似系數的計算公式；通過數值模擬將該方法與已有相似理論進行對比，以分析該方法的模型預測精度。

1 理論基礎

早期的相似理論認為：模型相當于從全尺寸原型上分離出的微元；除了尺寸與質量上的差異外，模型各物理量(如速度、應變率等)和外載條件均應與全尺寸原型相同。顯然，該理論忽視了因尺寸效應而產生的相似系數變化，故模型與全尺寸原型實驗結果相差較大。

自Π定理建立后，出現了MLT (mass-length-time)相似理論。該理論基于量綱一致原則提出，在確定基本物理量的相似系數后、其余物理量的相似系數均可通過Π定理求得。MLT相似理論中部分物理量的相似系數為：幾何長度，λ；體積，λ3；質量，λ3；時間，λ；速度，1；壓力，λ2；應力，1；應變，1；應變率，1/λ。

MLT相似理論對于(準)靜態實驗具有重要指導意義。但由于該理論對速度等特征參數計算的線性相似系數不夠精確，故在指導動態實驗時存在不足之處。

Calladine等[5]對MLT相似理論進行了修正、并提出Calladine相似理論。該理論將速度相似系數λv由1改為λ，相應的質量相似系數λm由λ3改為λ。這一做法在部分沖擊問題中取得了較好的結果，但在更一般的沖擊實驗中其預測結果誤差較大、普適性不足；故仍有改進的必要。

Oshiro等[6]從Norton-Hoff公式出發，提出了VSG (velocity-yield stress-mass)相似理論。Norton-Hoff公式[7]的表達式為 ：

(1)

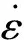
VSG相似理論的質量相似系數λm與MLT相似理論相同：λm=λ3；而速度相似系數λv為：

(2)

式中:λσ0是模型與全尺寸原型材料的(準)靜態屈服應力比，即λσ0=σ0m/σ0p；下標m、p分別代表模型(model)和全尺寸原型(prototype)。

VSG相似理論較好地解決了應變率效應對沖擊實驗結果造成的影響，但其并未考慮若模型與全尺寸原型使用不同材料制造時，質量相似系數的變化(VSG相似理論認為密度相似系數λρ=1)；同時Norton-Hoff公式參數較少、不能準確描述應變率效應的影響，因此還有改進空間。

2 模型修正

本文中給出基于VSG理論的、考慮模型與全尺寸原型使用不同材料制造的修正模型(稱之為VSG+方法)。首先引入與應變率相關的Cowper-Symonds公式[8]：

(3)

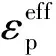
對于質量相似系數λm有：

(4)

在VSG相似理論中有

(5)

(6)

式中：λv的表達式中包含λv，故須通過迭代方法求解λv。

綜上所述，4種相似理論的質量相似系數λm與速度相似系數如表1所示。

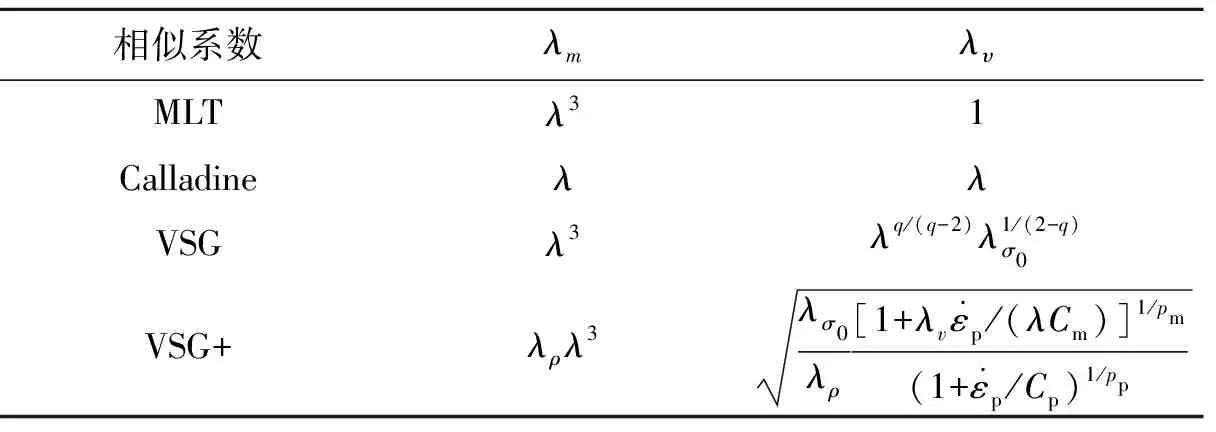
表1 4種相似理論質量相似系數與速度相似系數Table 1 Four theories’ mass factors & velocity factors

3 算例驗證

為驗證上述方法的有效性，引入簡化模型、在ABAQUS平臺下分別使用已有相似理論和本文中提出的VSG+方法，計算同一縮比尺寸下的沖擊實驗結果。通過數值模擬得到不同外載條件下模型的凹坑深度，并與全尺寸原型結果做對比。

簡化模型為一個四邊固支的正方形金屬板(邊長a=100 mm、厚度H=1 mm)受到直徑d=10 mm、質量m=20 g、初速度v0=100 m/s的剛性小球撞擊板中心部位，如圖1所示。

金屬板材料分別選用2024鋁合金(對應變率不敏感)和45鋼(對應變率敏感)，兩種材料部分參數如表2所示。

表2 材料參數Table 2 Parameters of the materials

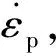
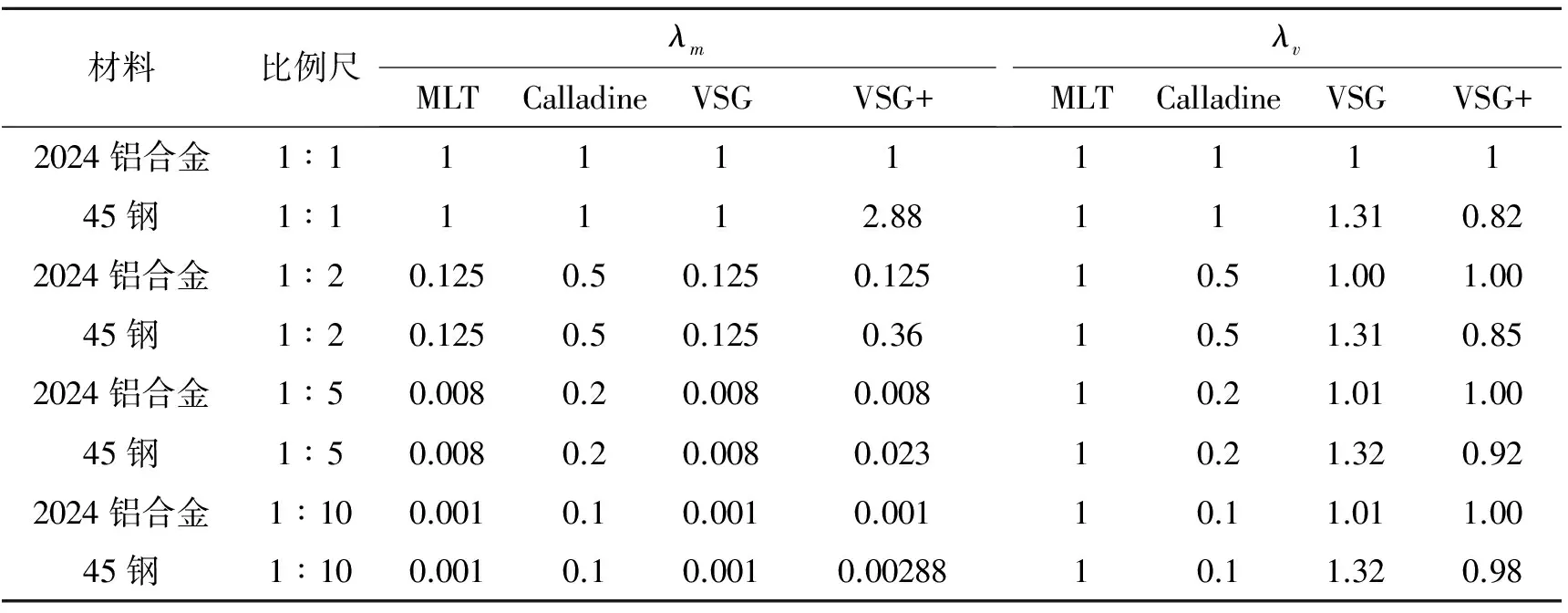
表3 不同材料及比例尺模型的初始外載條件Table 3 Initial conditions for models in different materials & scales

在ABAQUS軟件中建立模型并設定各參數，得到4種相似理論數值模擬結果如圖2所示。由于尺寸差異，縮比實驗結果已按比例尺放大。

從圖2(b)、(d)、(f)可看出，由于2024鋁合金無應變率效應影響，所以MLT、VSG和VSG+相似理論模型結果均與全尺寸原型結果吻合較好，而Calladine相似理論因其局限性故不適合本算例；從圖2(a)、(c)、(e)、(g)可以看出，模型在縮放后由于剛度上升，帶來的應變率效應影響也逐漸明顯。對比4種理論與全尺寸原型結果可以發現，本文中提出的VSG+相似理論相對于傳統相似理論，在建模精度上有了一定提高。

4 結 論

基于VSG相似理論，提出了若模型與全尺寸原型使用不同材料制造時考慮應變率效應的相似理論修正模型：稱之為VSG+方法。通過引入與應變率相關的Cowper-Symonds公式，重新計算了質量相似系數與速度相似系數。在與傳統相似理論對比后，證明該方法預測精度高于傳統理論。

本文中算例均采用典型材料，對于其他應變率敏感程度不同的材料及復雜模型(如復雜結構、復雜初始外載條件等)該理論的適用性，將作為今后研究重點進一步分析。

參考文獻:

[1] 沈雁鳴,陳堅強.超高速碰撞相似律的數值模擬驗證[J].爆炸與沖擊,2011,21(4):343-348.

SHEN Yanming, CHEN Jianqiang. Numerically simulating verification of the comparability rule on hypervelocity impact[J]. Explosion and Shock Waves, 2011,21(4):343-348.

[2] BAKER W E, WESTINE P S, DODGE F T. Similarity methods in engineering dynamics: theory and practice of scale modeling[M]. Amsterdam: Elsevier Science Publishers, 1991.

[3] 談慶明.高速沖擊模型律[M]∥王禮立.沖擊動力學進展.合肥:中國科學技術大學出版社,1992:303-320.

[4] 談慶明.量綱分析[M].合肥:中國科學技術大學出版社,2005.

[5] CALLADINE R C. An investigation of impact scaling theory[M]. London: Structural Crashworthiness, Butterworths & Co Publishers, 1983:169-174.

[6] OSHIRO R, ALVES M. Scaling of structures subject to impact loads when using a power law constitutive equation[J]. International Journal of Solids Structure, 2009,46(18/19):3412-3421.

[7] LEMAITRE J, CHABOCHE J L. Mechanics of solids materials[M]. Paris: Dunod, 1988.

[8] JONES N. Structural impact[M]. New York: Cambridge University Press, 1997.

[9] CHEN Liebin, YANG Jialing. Analytical evaluation of permanent deflection of a thin circular plate struck normally at its center by a projectile[J]. Acta Mechanica Solida Sinica, 2007,20(2):117-122.