側向點爆炸作用下地下拱結構的動力響應*
周忠欣,金豐年,袁小軍,陳海龍,周健南,徐 迎,孔新立
(陸軍工程大學國防工程學院爆炸沖擊防災減災國家重點實驗室,江蘇 南京 210007)
目前針對地下結構除基于核爆炸或模擬核爆炸作用外的研究,基于常規武器爆炸的研究也逐漸備受重視[1-3]。但由于結構與介質之間復雜的相互作用,對地下拱形結構的研究較少。陳海龍等[4]利用簡化的拱形振動方程,給出爆點位于拱形結構正上方處的彈性動力響應解析解。然而,由于爆炸荷載位置的不確定性,側向爆炸荷載作用對結構的響應研究更具有適用性。楊昇田等[5]根據大量試驗和數值分析得到側向爆炸作用下直墻拱頂襯砌動力響應解析解,同時給出壓力函數的解析表達式。計算結構-介質之間的相互作用常見于2種方式:MSSI(modified soil-structure interaction)理論和Constantino相互作用理論。Miller等[6]、Weidlinger等[7]利用這2種理論計算了結構和介質之間的動力響應。陳海龍等[8]將爆炸荷載簡化為側向均布荷載,對遠場情況任意角度荷載作用下結構響應進行計算,得到了側向荷載作用下結構的位移分布曲線。孫惠香等[9]、Henrych[10]利用有限元等方法對爆炸荷載作用下地下拱形結構與圍巖的相互作用進行了研究。本文中,采用Henrych振型假設[10]與MSSI模型,理論推導非均布側向爆炸荷載作用下拱結構的位移、速度和加速度等時程響應,以期獲得更符合實際工況的響應結果。計算中假設爆點距離結構較遠,對結構未造成較大程度破壞,結構處于彈性響應階段。
1 側向爆炸土中自由場荷載和位移
1.1 土中自由場荷載和位移
計算土中自由場峰值壓力p0(R)和峰值位移w0(R)時,采用TM5-855-1[11]中給出的公式:
(1)
(2)
式中:f為耦合因數,其與比例爆距有關;ρs為土體介質密度,kg/m3;cs為地震波波速,m/s;R為考察點至裝藥中心的距離,m;WTNT為等效TNT裝藥的質量,kg;n為直接地沖擊在介質中的衰減因數。
一般,地下爆炸產生的自由場荷載的時程函數和位移的時程函數可用指數衰減函數形式來表示:
σi(R,t)=p0(R)e-t/t0
(3)
wi(R,t)=w0(R)e-t/t0
(4)
式中:t為作用時間,s;t0為沖擊波從爆點至結構的傳播時間,s。
在工程應用時,通常可將指數衰減函數簡化為突加三角形荷載:
(5)
式中:td為等效荷載持續時間,s。此時空間自由場荷載和位移可以表示為
σi(R,t)=p0(R)f(t)
(6)
wi(R,t)=w0(R)f(t)
(7)
1.2 結構表面自由場荷載和位移
如圖1所示,當爆炸點發生在C點時,產生的沖擊波在土中傳播,作用在拱結構表面,在結構上i點處承受爆炸方向土壓力σi(R,t),由于土壤與結構的相互作用,會產生側向土壓力νσi(R,t)/(1-ν)。因此,結構表面實際載荷、位移關系為:
σfi(φ,θ,t)=
(8)
wfi(φ,θ,t)=wi(R,t)cos(θ+φ)
(9)
式中:ν為土壤泊松比;θ=θ1+θ0;θ1為作用點法線方向與豎直方向夾角,計算中規定θ1以Y軸為起始點,向第二象限旋轉為正,向第一象限旋轉為負;θ0為拱頂點方向與起爆點方向之間的夾角,規定θ0在第一象限為正,在第二象限為負;φ為入射應力波方向與起爆點法線方向之間的夾角。
由幾何關系可以得到:
根據幾何關系,將式(8)、(9)化為關于θ1、θ0的函數:
(10)
(11)
式中:L2=x2+(H+r)2,r為拱的半徑,R為起爆點到作用點的距離,H為拱的埋深,x為起爆點到拱正上方點的水平距離,L為起爆點與拱心之間的距離,定義S2=r2-R2。
當θ1=-θ0時,即作用點與起爆點之間的連線為法線方向時,可得到拱結構上距離起爆點最近距離處自由場荷載和位移:
σfi(-θ0,θ0,t)=σi(L-r,t)
(12)
wfi(-θ0,θ0,t)=wi(L-r,t)
(13)
設ξ=r/H,將方程(11)化為關于ξ、θ1、θ0的載荷分布形式:
(14)
式中:
設ξ=r/H,將方程(12)化為關于ξ、θ1、θ0位移分布形式:
(15)
式中:
根據式(14)、(15),在當θ0=30°,給定ξ時,可以得到對應作用在結構處自由場荷載、位移的分布形式。如圖2(a)所示,當ξ不變時,隨著衰減系數n的減小,結構表面自由場荷載的分布趨于平緩,局部荷載效應減弱,且最大值作用點對應的位置為起爆點的法線方向。圖2(b)所示,隨著衰減系數減小,位移的分布形式也趨于平緩,局部變形作用減弱。
圖3表明,當衰減系數保持不變時,隨著ξ的減小,爆點與結構之間的距離增大,結構的局部效應減弱,分布范圍增大。當ξ增大時,位移變形的分布規律更類似于三角形分布,位移變形較為集中,對結構局部的損害較明顯。
如圖4(a)所示,隨著角度的增加,偏移距離增大,各自由場沖擊荷載的分布曲線的峰值點也隨之偏移,且隨著距離的增大,峰值逐漸降低,分布范圍增加,局部效應減弱。如圖4(b)所示,隨著角度的增大,各位移曲線的峰值點也隨之偏移,且隨著距離的增大,峰值逐漸降低,出現位移的范圍增加,結構的局部效應減弱。對結構的破壞影響較小。
2 結構振動方程
埋地拱結構與周圍土體之間有一定的相互作用,運用MSSI理論得到結構表面的荷載分布形式:
(16)
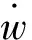
2.1 薄拱的振動方程
對Henrych的拱的振動方程[10]進行簡化,得:
(17)
式中:r為圓拱結構單元半徑,E為楊氏模量;ω為自振頻率;A為矩形截面,I為截面慣性矩;m為單元質量,m=ρA,ρ為密度;v(θ1,t)為切向位移;qw為徑向外力。且:
(18)
對于彈性拱結構,利用振型的疊加,結構的位移函數可以表示為:
(19)
式中:k為序數。將方程(16)、(17)代入方程(18)中,化簡可得:
(20)
根據振型的正交性,將公式(20)化簡,得:
(21)
當對荷載時程函數不做簡化時,f(t)=e-t/t0,因此在計算結構動力響應時,式(21)為:
(22)
式中:
2.2 結構彈性動力響應
(1)過阻尼情況時,ξk>1,對式(22)進行求解:
(23)
根據公式(7),有:
(24)
速度函數、加速度函數分別為:
(2)欠阻尼情況時,ξk<1,對方程(22)進行求解:
(25)
根據公式(7),有:
wk(θ1,t)=wk(θ1)fk(t)=
(26)
速度函數、加速度函數為wk(θ1,t)的一階、二階導數。
3 算 例
3.1 土體聲阻抗的影響
結構兩端固支,拱的整體角度為110°,在計算側向偏移過程中,ξk=2,拱的半徑為6 m,水平偏移距離為5.2 m,即θ0=30°,楊氏模量為29 GPa,炸藥量為8 kg,拱的埋深為3 m,混凝土拱截面A=1 mm×0.8 mm,設爆炸荷載作用時間為15 ms。選擇3種土壤進行比較,3種土的性質見表1,當土體聲阻抗不同時,對爆炸點與拱圓心連線處拱上的拱點的位移、速度、加速度進行比較。

表1 3種土壤的相關參數Table 1 Properties of three soils
從圖5可以看出,不同土壤有不同的聲阻抗,聲阻抗越大結構在土中的位移越大,結構速度達到最大值的時間越短。而聲阻抗對加速度影響更為明顯,加速度在荷載作用的瞬間即達到最大值,然后隨著時間的推移,加速度逐漸減小。可以得出,在結構承受荷載時,當結構所在的土體聲阻抗越小,對結構造成的影響越小。
3.2 比例爆距對結構動力響應的影響
在計算時,比例爆距選擇的范圍為0.5~3.0 m/kg1/3,爆炸計算模型取遠場爆炸進行研究。不同比例爆距下結構動力響應最大值如圖6所示。從圖6可以得出,土體聲阻抗越大,結構在各比例爆距下的位移、速度、加速度均增大;且隨著比例爆距的增大,結構響應在減小。當比例爆距值為3.0 m/kg1/3時,結構上的最大動力響應趨于零,呈收斂趨勢。
4 結 論
(1)當爆點位于不同位置時,荷載作用范圍也會發生變化,導致不同的結構動力響應。
(2)隨著衰減系數的減小,結構表面自由場荷載的分布趨于平緩,局部荷載效應減弱,且最大值作用點對應的位置為起爆點的法線方向。
(3)隨著偏移距離的增大,荷載與位移的各分布曲線的峰值點也隨之偏移,且隨著距離的增大,峰值逐漸降低,分布范圍增加,局部效應減弱,對結構的損傷也在衰減。
(4)聲阻抗與結構動力響應呈正比,比例爆距與結構動力響應呈反比;因此防護結構周圍應選擇在聲阻抗較小的介質中構筑。
參考文獻:
[1] WANG Zhongqi, LU Yong, HAO Hong, et al. A full coupled numerical analysis approach for buried structures subjected to subsurface blast[J]. Computers and Structures, 2005,83(4/5):339-356.
[2] MA Guowei, ZHOU Hongyuan, LU Yong, et al. In-structure shock of underground structures: A theoretical approach[J]. Engineering Structures, 2010,32(12):3836-3844.
[3] KIGER S A, DALLRIVA F D, HALL R L. Dynamic skin-friction effects on buried arches[J]. Journal of Structural Engineering, 1989,115(7):1768-1781.
[4] 陳海龍,范華林,金豐年.爆炸荷載作用下地下拱結構動力分析[J].工程力學, 2012,30(4):169-174.
CHEN Hailong, FAN Hualin, JIN Fengnian. Forced vibration of underground clamped arch under arch under blast load[J]. Engineering Mechanics, 2012,30(4):169-174.
[5] 楊昇田,曹志遠.地下結構與巖體動力相互作用的一種解析解[J].應用數學和力學,1983,6:861-868.
YANG Shengtian, CAO Zhiyuan. An analytical solution for underground structure-country rock dynamic interaction[J]. Applied Mathematics and Mechanics, 1983,6:861-868.
[6] MILLER C A, COSTANTINO C J. Structure- foundation interaction of a nuclear power plant with a seismic disturbance[J]. Nuclear Engineering and Design, 1970,14(2):332-342.
[7] WEIDLINGER P, HINMAN E. Analysis of underground protective structures[J]. Journal of Structural Engineering, 1988,114(7):1658-1673.
[8] 陳海龍,金豐年,夏志成,等.側向爆炸作用下地下拱結構動力響應[J].巖石力學與工程學報,2012,31(增刊2):3478-3481.
CHEN Hailong, JIN Fengnian, XIA Zhicheng, et al. Dynamic response of underground arch structure under side blast load[J]. Chinese Journal of Rock Mechanics and Engineering, 2012,31(suppl 2):3478- 3481.
[9] 孫惠香,許金余.爆炸荷載作用下地下結構與圍巖動力相互作用研究[J].土木工程學報,2011,44(增刊):148-151.
SUN Huixiang, XU Jinyu. Dynamic action study between structure and rock of underground structure subjected to blast load[J]. China Civil Engineering Journal, 2011,4(suppl):148-151.
[10] HENRYCH J. The dynamics of arches and frames[M]. Amsterdam: Elsevier, 1981.
[11] Department of the Army. Technical Manual TM 5-855-1: Fundamentals of protective design for conventional weapons[M]. Washington, DC, USA: Department of the Army, 1986.

