單軸雙向加載分離式霍普金森壓桿的數據處理方法*

聶海亮，石霄鵬，陳春楊，李玉龍

(西北工業大學航空學院,陜西 西安 710072)

霍普金森壓桿實驗技術自1914年被提出以來[1]，經歷了一百余年，已成為材料動態力學性能測試的一種最重要手段[2-4]。目前廣泛使用的技術是Kolsky[5]在1949年提出的一種分離式霍普金森壓桿(split Hopkinson pressure bar，SHPB)。傳統的SHPB通過撞擊桿與入射桿的同軸碰撞產生壓縮波，沿入射桿傳播，并對試樣進行加載[6]。SHPB一般被用來測量材料在高應變率下的塑性流動行為，在加載的最初階段，試樣兩端的應力還未達到均勻，實驗數據的可信度比較差，導致計算的材料特性在彈性段有部分無效數據。當應力波在試樣中來回反射3～5個來回后，試樣兩端的應力達到均勻，實驗數據才有效[7]。為了測量波阻抗較低的軟材料，Wang等[8]提出用波阻抗較低的聚合物桿取代傳統的金屬桿。Hou等[9]提出了一種用于測量泡沫材料動態壓剪力學性能的SHPB裝置，將入射桿和透射桿與試樣的接觸端面改為斜面以產生壓剪效應。崔云霄等[10]在此基礎上設計了一種雙透射桿的SHPB裝置。這些改進都收到了良好的效果。鑒于傳統SHPB加載方式中單向加載對試樣內部應力平衡的影響，本文中提出一種單軸雙向加載分離式霍普金森壓桿(bidirectional-load split Hopkinson compression bar,BSHCB)實驗技術，即在傳統SHPB的基礎上增加另一個對稱的入射波，兩邊的入射波同時且對稱地對試樣進行動態加載。基于一維應力波傳播理論，推導出單軸雙向加載分離式霍普金森桿的數據處理公式，并通過有限元模擬對公式的可靠性進行驗證。

1 加載方式及數據處理公式

1.1 實驗加載原理

BSHCB裝置如圖1所示。在傳統的SHPB裝置的基礎上，將透射桿作為另一根入射桿，通過2個應力波發生裝置從2根入射桿端面同時輸入2個相同的入射波，2根壓桿長度相同，因此2個入射波會同時到達試樣，對試樣進行對稱加載。

1.2 數據處理公式推導

記2根入射桿分別為桿1和桿2，如圖2所示。在2列入射波εi1和εi2對試樣加載過程中，會分別在相應的入射桿中產生一列與入射波傳播方向相反的波，分別記作反射波ε1和ε2。

忽略彌散效應等非一維效應，根據應力波理論，端面1和端面2處的質點速度為:

v1=c0(εi1-ε1),v2=c0(ε2-εi2)

(1)

于是，試樣中的平均工程應變率和平均工程應變分別為:

(2)

(3)

式中：c0為壓桿中的彈性波速，ls為試樣的初始長度，td為入射波持續時間。

試樣兩端的應力分別為：

(4)

式中：Ab和As分別為壓桿和試樣的橫截面積，E為壓桿的彈性模量。

試樣內部的應力取兩端面的應力平均值：

(5)

若兩端的加載完全對稱，即εi1=εi2，試樣中截面相當于剛壁，將兩邊分為2個對稱的子系統，因此有ε1=ε2。式(2)、(3)和(5)即簡化為:

(6)

式(2)、(3)和(5)適用于單軸雙向加載的一般情況下的材料特性計算，式(6)適用于兩端加載的入射波完全對稱的情況。

2 有限元模擬過程

本節采用商業軟件Abaqus/explicit模塊進行數值模擬，對BSHCB的數據處理公式進行驗證。

在模擬中，壓桿長1 m，直徑為10 mm。壓桿材料為鋼，彈性波速為5 188.75 m/s，密度為7 800 kg/m3,楊氏模量為210 GPa。試樣材料為2024鋁合金，采用Johnson-Cook本構模型。Johnson-Cook本構模型[11]是經驗型本構方程，由2部分組成：第1部分只涉及應力，第2部分則涉及斷裂時的應變。在本文的模擬中只涉及第1部分的內容，von Mises流動應力σM的計算公式為:

(7)

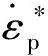
首先給兩邊加載脈寬為150 μs、上升沿為10 μs、幅值為300 MPa的相同的梯形波，通過公式處理和試樣上一點處的應力-應變曲線進行比較，來驗證公式的正確性。

采用二維軸對稱模型以減小計算時間。通過網格敏感性分析，發現當全局網格尺寸約在0.8 mm時，網格對結果無影響。由于本文中采用軸對稱二維模型，網格數量較少，運算速度較快，為了提高運算精讀，將全局網格尺寸設置為0.2 mm。入射波均以壓桿端面上的壓強脈沖的形式輸入模型。壓桿上的應力波信號均取自兩根桿軸向中截面處的表面單元，每隔0.5 μs取一個數據。

3 結果及分析

3.1 試樣內部應力分析

為了驗證所推導的數據處理公式的正確性，需知道試樣內部實際的工程應力-工程應變曲線。在數值模擬中，擬在試樣中心點處上取一個單元的工程應力-工程應變曲線，來代表材料的實際力學特性。為了驗證，分別在試樣表面、半徑一半處以及試樣對稱軸處各取一組代表單元，分別命名為Surface、Half和Axes，每組代表單元由沿軸向每隔4個單元所取的所有單元組成，如圖3(a)所示。將試樣中心點處的單元命名為Center。分別對每組單元的工程應力歷程和工程應變歷程取平均值，得出平均的工程應力-工程應變曲線。同時，取Center單元的工程應力-工程應變曲線進行比較。圖3(b)給出了3組單元的平均工程應力-工程應變曲線與Center單元的工程應力-工程應變曲線。顯然，Center單元的工程應力-工程應變曲線與Surface、Half、Axes的工程應力-工程應變曲線完全重合。因此，可以認為試樣中心點處的單元應力狀態能夠代表試樣內部的實際應力狀態。因此，在后面的對比中，都取試樣中心點處單元的應力狀態來代表所模擬的實際應力狀態。

3.2 公式有效性驗證

單軸雙向對稱壓縮加載情況為300 MPa VS 300 MPa時，在2根壓桿的中取到的應力波信號如圖4(a)所示。由于是對稱加載，2根桿中所采集的應力波信號完全重合，為了便于觀察，將2列波在時間上錯開。對圖4(a)中所記錄的應力波進行移波并保留有用波形，便得到圖4(b)所示的處理波形。

用公式(6)對圖4(b)的數據進行處理，得到300 MPa VS 300 MPa時試樣的工程應力-工程應變曲線，繪制在圖5中，并與在試樣中心點處的單元上所取的工程應力-工程應變曲線進行對比。很明顯，計算的工程應力-工程應變曲線與試樣內部的實際工程應力-工程應變曲線幾乎完全重合，從而驗證了1.2節中所推導的對稱加載公式的正確性。

在圖4中，反射波ε1有一部分為拉伸波，一部分為壓縮波，這實際上是壓桿中的應力波疊加的結果。當入射波到達端面1時，會產生反射波(拉伸波)和透射波(壓縮波)，由于對稱性，端面2處相同，方向相反。當2道對稱壓縮波在試樣中心相遇發生相互作用時，由對稱性可知，試樣中心位移為零(剛壁)，將產生2道壓力更高的壓縮波分別向端面處傳播(可視為剛壁的反射，也可視為對面透射過來的，但已不是原來那個透射波了)，具體增加的幅值取決于材料當時的性質，線彈性時，增加一倍。再經過端面處作用，最后形成桿中的反射波。所以實際中采集到的反射波ε1不是一個單純的壓縮波或拉伸波。

4 討 論

在本節的討論中，對比在入射波形完全相同的情況下，單向加載和雙向加載的差異。所用模型參數與第2節相同，唯一的區別之處在于，單向加載模擬中只有一個入射波，雙向加載時在2個入射桿中施加相同的入射波。

4.1 應力均勻性

為了直觀地比較單向加載與雙向加載方式在試樣應力均勻性方面的差異，定義試樣內部應力差異因子α。對于傳統的SHPB方式，試樣兩端面的應力差異最大，而對于BSHCB方式來說，試樣兩端的和中截面處的應力差異最大。因此，對于傳統的SHPB加載方式,α=|σ1-σ2|/σe;而對于BSHCB方式,α=|σe-σm|/σe;式中σe為試樣的兩端面的應力平均值，σm為試樣中部截面上的應力平均值。

圖6為單軸雙向加載與常規加載方式中加載初期試樣內部的應力分布，在模擬中，單向加載和雙向加載所施加的入射波均為梯形波，幅值相同，上升沿為10 μs。假定α<0.05時，試樣內部應力達到均勻。令τ為應力波在試樣中傳播一個試樣長度所用的時間，由試樣的材料特性和尺寸可知，τ≈1 μs。顯然，對于雙向加載方式，在約4τ后試樣內部的應力就達到了均勻分布，而對于傳統的單向加載方式，試樣在約12τ后才基本達到應力均勻狀態。因此，雙向加載中試樣達到應力均勻狀態的時間是單向加載的1/3。這是因為對雙向對稱加載來說，試樣中點為對稱不動點，因此試樣內部應力波的反射距離僅為試樣厚度的1/2，從而加快了應力均勻化。

由以上分析可知，單軸雙向加載方式中，試樣能夠在更短的時間內達到應力均勻狀態。

4.2 應變率的提高

同傳統的SHPB方式相比，BSHCB方式因為多了一個入射波，所得到的材料應變率必然會高于比相同載荷下的SHPB方式。為了便于比較應變率的提高，應變率-時間曲線應保持基本的恒定。

在雙向對稱加載中，根據單軸雙向加載的試樣材料應變率計算公式可知，試樣的應變率-時間曲線與入射波和反射波差值的波形有關。結合圖4(b)中的反射波形可知，對于本文所模擬的材料，在入射波為梯形波的情況下，入射波與反射波之差不存在平臺段，而是在一個急劇上升的峰值之后出現一個下降的斜坡，因此試樣變形的應變率并不是恒定的，而是先急劇增大，再緩慢減小。為了使計算的材料應變率-時間曲線有一個基本恒定的平臺段，應該使入射波在上升沿之后有一個緩慢上升的斜坡段，以抵消反射波產生的下降沿斜坡。通過數值模擬的多次嘗試，得到了一個使應變率基本恒定的入射波形。圖7(a)為單軸雙向對稱加載下2根壓桿上所采集到的應力波信號，圖7(b)為所計算的工程應力-工程應變曲線和工程應變率-工程應變曲線。顯然，在圖7(a)的入射波加載條件下，模擬計算所得到的試樣工程應變率-工程應變曲線在在材料的塑性變形階段保持了基本恒定的值。

同樣的入射波被用于相同條件下的SHPB模擬，圖8對比了SHPB加載和BSHCB加載的模擬結果。顯然，BSHCB加載的應變率比SHPB加載高了一倍左右。

實際上，雙向對稱加載時，試樣的中心面相當于剛壁，從試樣長度看，相當于試樣長度縮短了一半，故應變率會提高一倍，同時，由于剛壁的強烈反射，應力迅速升高，高應力使得材料應變大幅增加(取決于材料的性能)，因此相同脈寬下，應變率至少提高一倍，甚至更高。

雙向對稱加載時，由于壓桿的屈服強度有限，為了避免壓桿中的應力水平超過壓桿的屈服極限，對入射波的幅值有特殊的要求。以入射桿1為例，在靠近試樣的端面，壓桿內的應力水平最高為2σ1。為了避免壓桿內的應力水平超過壓桿材料的屈服極限，BSHCB加載中的入射波幅值不能超過壓桿屈服極限的一半。

4.3 加載不對稱的問題

實際中，2根壓桿中的入射波幅值會存在微小差異，絕對對稱加載是無法實現的。本節對偏離對稱加載的情況進行討論。本文中所推導的數據處理公式允許2個入射波存在不對稱性。當兩邊入射不對稱時，采用公式(2)、(3)和(5)即可處理。

對于加載幅值的不對稱，在模擬中令一邊的梯形入射波的脈寬為150 μs、上升沿為10 μs、幅值為300 MPa,保持不變，而另一邊的入射波幅值減小ΔA。圖9(a)所示為ΔA分別等于0%、10%、20%、30%、40%以及50%時所得到的數值實驗結果。可以看出，當兩端加載的入射波幅值存在差異時，實際上是改變了試樣的應變率。差異越大對應變率的改變越大。由于試樣材料對應變率不敏感，所以在圖9(a)中，應變率的不同體現在最大應變的差異上。模擬中給出的最大幅值誤差為50%，而在實際中，兩端加載波的幅值差異不可能這么大。以上分析可知，單軸雙向加載中允許兩端的加載波幅值存在差異。當兩端加載波幅值存在差異時，僅僅影響所測材料的應變率，而不會對數據的有效性造成影響。

實際實驗中，絕對同步也是無法達到的，特別是霍普金森桿這種時間在微秒量級的實驗。而兩邊入射波不同步的問題可以轉化為兩邊波形不同的問題，即認為滯后的入射波在加載前有一段幅值為零。

令τ=ls/cs作為特征時間，其中，ls和cs分別為試樣的長度和試樣材料彈性波速。通過數值模擬來比較2個加載波不同步時所得的工程應力-工程應變曲線。圖9(b)所示為兩邊加載波時間差分別為0、5、10、15、20倍的特征時間時得到的工程應力-工程應變曲線的比較。從模擬結果看，2個加載波不同步對實驗結果的準確性影響不大。在不同步情況下，在延遲的入射波到達試樣之前，已經在該桿中存在一個從另一根桿中傳遞過來的應力波，因此，為了保證從壓桿軸向中點處所測的入射波和反射波形不會疊加，2列入射波的時間差Δt應該滿足(Δt+td)cs<2l,l為應變片到壓桿與試樣接觸面的距離。另外，入射波之間的延遲時間最大不能超過一個入射波長，否則會產生二次加載，從而導致實驗結果不準確。

實際上，從理論上很容易理解上述分析結果。對于試樣內部的應力均勻化過程，傳統的SHPB加載方式和對稱加載方式是2個極端情況，而不對稱加載則是介于兩者之間的一般情況，因此試樣內部的應力均勻化時間也介于兩者之間。

4.4 BSHCB實驗裝置研制情況

傳統的SHPB采用高速子彈撞擊入射桿的方式產生應力波，這種方式很難同時產生2個對稱的入射波。近年來，采用電磁能量裝換技術實現應力波的產生[12-13]，不同于傳統的加載方式，這種技術將LC電路儲存的電磁能量直接轉化成用于實驗的應力波。應力波的特征依賴于LC電路的放電電流，因此能夠保證應力脈沖產生時間和波形的精確控制。目前該技術已經取得了良好的效果，圖10給出在實際實驗中測到的2個入射桿中的應力波形，2根入射桿完全相同，直徑為14 mm，長度為3.5 m，中間未裝試樣，2對應變片與應力波輸入端的距離相同。從實驗結果可以看出2個入射波幅值和時間誤差很小。在實驗中，2個入射波之間的時間差約2 μs ，幅值誤差在5%以內，因此這一應力波發生技術可以應用于BSHCB。另外，圖10為單個LC電路放電所產生的應力波，是半正弦脈沖，通過多個LC電路的時序放電，可以產生不同形狀的應力脈沖[14]，因此該技術在未來可以應用于單軸雙向加載實驗中2個入射波的產生。

5 結 論

提出了單軸雙向加載分離式霍普金森桿(bidirectional-load split Hopkinson compression bar,BSHCB)，通過應力波理論推導出了單軸雙向加載的數據處理公式，并用數值模擬的方法對公式的正確性進行了驗證，得到以下結論：

(1)所推導的BSHCB的數據處理公式可以計算所測材料的工程應力、工程應變和工程應變率；

(2)單軸雙向對稱加載可縮短試樣內部應力均勻化的過程，可以改善材料動態性能在彈性段測量的可靠性；

(3)同傳統的SHPB技術相比，在相同條件下，BSHCB所得到的試樣應變率至少提高一倍，因此能夠擴展材料動態力學實驗所達到的應變率范圍；

(4)所推導的BSHCB數值處理公式允許試樣兩端的加載條件存在不對稱性，可以用于材料的變應變率測試或二次加載測試。

感謝周風華老師對本文提出的修改意見，感謝苗應剛博士對本文修改過程中的幫助。

參考文獻：

[1] HOPKINSON B. A method of measuring the pressure produced in the detonation of high explosives or by the impact of bullets[J]. Philosophical Transactions of the Royal Society of London, 1914,213(612):437-456. DOI: 10.1098/rspa.1914.0008.

[2] GARY G, MOHR D. Modified Kolsky formulas for an increased measurement duration of SHPB systems[J]. Experimental Mechanics, 2013,53(4):713-717. DOI: 10.1007/s11340-012-9664-7.

[3] NIE X, PRABHU R, CHEN WW, et al. A Kolsky torsion bar technique for characterization of dynamic shear response of soft materials[J]. Experimental Mechanics, 2011,51(9):1527-1534. DOI: 10.1007/s11340-011-9481-4.

[4] LIM J, CHEN W W, ZHENG J Q. Dynamic small strain measurements of Kevlar 129 single fibers with a miniaturized tension Kolsky bar[J]. Polymer Testing, 2010,29(6):701-705. DOI: 10.1016/j.polymertesting.2010.05.012.

[5] KOLSKY H. An investigation of the mechanical properties of materials at very high rates of loading[J]. Proceeding of the Physical Society, 1949,62(11):676-700. DOI: 10.1088/0370-1301/62/11/302.

[6] SONG B, GE Y, CHEN W W, et al. Radial inertia effects in Kolsky bar testing of extra-soft specimens[J]. Experimental Mechanics, 2007,47(5):659-670. DOI: 10.1016/j.polymertesting.2010.05.012.

[7] PARRY D J, DIXON P R, HODSON S, et al. Stress equilibrium effects within Hopkinson bar specimens[J]. Journal De Physique IV, 1994,4(C8):107-112.DOI: 10.1051/jp4:1994816.

[8] WANG L L, LABIBES K, AZARI Z, et al. Generalization of split Hopkinson bar technique to use viscoelastic bars[J]. International Journal of Impact Engineering, 1994,15(5):669-686. DOI: 10.1016/0734-743X(94)90166-I.

[9] HOU B, ONO A, ABDENNADHER S, et al. IMPact behavior of honeycombs under combined shear-compression. Part I: Experiments[J]. International Journal of Solids and Structures, 2011,48(5):687-697. DOI: 10.1016/j.ijsolstr.2010.11.005.

[10] 崔云霄,盧芳云,林玉亮,等.一種新的高應變率復合壓剪實驗技術[J]. 實驗力學,2006,21(5):584-590.DOI: 10.3969/j.issn.1001-4888.2006.05.007.

CUI Yunxiao, LU Fangyun, LIN Yuliang, et al. A new combined compression-shear loading technique at high strain rates[J]. Journal of Experimental Mechanics, 2006,21(5):584-590. DOI: 10.3969/j.issn.1001-4888.2006.05.007.

[11] JOHNSON G R, COOK W H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures[J]. Engineering Fracture Mechanics, 1985, 21(1):31-48. DOI: 10.1016/0013-7944(85)90052-9.

[12] 李玉龍,聶海亮,湯忠斌,等.基于電磁力加載的分離式霍普金森壓桿實驗裝置:CN201410161610.X[P].2014-07-09.

[13] 李玉龍,聶海亮,湯忠斌,等.一種基于電磁力的拉伸及壓縮應力波發生器及實驗方法:201410171963.8[P].2014-08-20.

[14] 李玉龍,聶海亮,湯忠斌,等.電磁式應力波發生器的主線圈及充電/放電的方法:201510051071.9[P].2015-06-03.