低失真爆炸沖擊信號零漂分析和處理方法*

張文偉，龐家志，楊仕超，翟 疆

(航天科工防御技術研究試驗中心，北京 100854)

固體燃料飛行器的任務剖面中，爆炸沖擊環境嚴酷。在環境測試和地面復現環境試驗中，極易出現零漂現象，究其原因，多數是由于傳感器、放大器飽和或傳感器電纜噪聲等測試系統噪聲造成的，也有部分是由于傳感器與被測產品之間的連接剛度不夠造成的[1-3]。爆炸沖擊由于安裝狀態對沖擊波的傳遞影響大、可復現性低，同時，點火沖擊試驗多具有破壞性，一次沖擊試驗完成后，試驗樣品也基本是損傷報廢了。因此，當沖擊數據采集完成后，如發生零漂現象，對數據進行修正處理后應用成為了大多數工程應用的必然抉擇[4-5]。

零漂現象是由于傳感器與被測產品中間的連接剛度不夠，或由于產品結構在受到沖擊時，發生了不可恢復的變形或滑移造成的。這類沖擊信號是不可修正的，難以判斷其是否為產品結構的沖擊響應特征，還是信號采集的零漂誤差。由放大器飽和造成的零漂，信號的低頻部分具有典型的電容放電特征，信號沒有削波現象發生的情況下，認為信號放大器出現了輕度飽和，造成所測電壓疊加了擁堵電壓誤差，此類誤差能通過有效的信號分離手段進行信號修正[6-8]。

本文中針對這類由于放大器飽和造成的零漂，詳細分析了零漂現象產生的原因和現行的數據修正方法，對比各修正方法的優缺點，提出了基于經驗模態分解(empirical mode decomposition, EMD)結合頻域窗函數濾波的新修正方法，能夠較好彌補現行修正方法的缺陷。

1 零漂成因分析

爆炸沖擊時間短，量級大，在爆炸沖擊信號測量中，大多會出現零漂現象。零漂產生的原因較為復雜，在無法分析鑒別零漂產生原因的情況下，相當一部分零漂誤差無法找到合理的理論依據進行修正處理。造成爆炸沖擊零漂誤差主要原因有：

(1)壓電晶體的磁疇變化造成零漂。高量級沖擊激勵下，傳感器由于自身的諧振響應，會導致過大的應力，造成壓電晶體磁疇的變化，磁疇將隨著應力、電磁場和溫度等環境因素的變化而達到新的平衡，磁疇的變化過程反映到傳感器輸出信號中，形成零漂誤差。

(2)壓電晶體的微量運動。壓電晶體相對于質量塊與基體的微量運動會造成傳感器的輸出零漂。傳感器基體與被測件由于連接剛度低，在沖擊激勵下，傳感器與被測件之間的微量運動也會形成零漂。從傳感器結構來看，壓電式沖擊傳感器有壓縮型和剪切型，如圖1所示。壓縮型傳感器，在裝配過程中，需要通過緊固螺釘對壓電晶體施加預緊力來產生線性輸出。沖擊應力超出預緊力時，慣性質量塊與壓電晶體之間會發生微量移動，導致輸出傳感器輸出零漂現象。壓縮性傳感器在側向沖擊力作用下，輸出零漂現象更為嚴重。剪切型傳感器無須施加預緊力，抗零漂能力較強。

(3)電纜噪聲。電纜與傳感器之間的連接松動及接頭附近電纜固定不牢固，在沖擊力作用下，電纜發生較大位移的抖動，由于電纜彎曲拉伸靜電摩擦效應產生感應電荷，相對于傳感器輸出的微弱電荷號，會形成顯著的零漂誤差。

(4)傳感器基座應變引起零漂。在大量級沖擊下，基座會承受較大的應力波，產生較大的應變，可導致壓縮型傳感器預緊力的變化，壓電晶體相對基座和質量塊也會發生微量滑移而產生零漂。剪切型傳感器的基座應變向壓電晶體傳遞過程中，被極大的削弱，所以剪切型傳感器抗基座應力能力較強。

(5)信號放大器飽和。測量信號的電壓變化速率，與信號頻率相關。放大器輸出電壓信號為Usin(2πft)，則輸出電壓信號的變化速率為：

(1)

放大器輸出信號的電壓變化速率為2πfmaxU，與放大器最大輸出電壓U和輸入信號的最大頻率fmax相關。放大器的電壓最大變化速率即壓擺率由輸出電路參數所決定，輸出信號電壓的最大變化速率應小于放大器的壓擺率:

(2)

即：

(3)

式中：I為放大器輸出電流，C為放大器輸出負載電容。

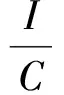
上述產生零漂的各個因素中，非放大器飽和造成的零漂，從信號特性上看，很難辨識出其是否是由于結構本身的響應引起的誤差，還是是測量系統引起的零漂誤差。如在明確知道沖擊激勵點至測量點之間傳遞關系的情況下，可以以傳遞關系來判斷信號的修正可用性。多數情況下，認為此類零漂誤差，在無法辨識因由和特征的情況下，是不可以進行合理修正后使用的，測量結果視作無效。對于由輕度放大器飽和引起的零漂誤差，其來源明確、信號特征顯著，認為可以通過合理的信號分離去噪處理進行修正。輕度放大器飽和引起的零漂信號具有兩個特征，如圖2所示。

圖2中顯見零漂呈現指數衰減規律，與RC電路放電曲線類似，同時加速度峰值也沒有出現平頂削波現象。從這兩個信號特征可以判斷信號放大器出現了輕度飽和，產生了零漂誤差。

2 信號去零漂處理

在爆炸沖擊中，由于信號頻帶寬、高頻能量大，沖擊測量極易產生放大器飽和引起的零漂。當前主要的信號修正方法有三種：最小二乘法、小波方法和EMD方法[9-11]。

2.1 最小二乘法

在離散信號數據采集與分析處理中，由于各種原因存在趨勢噪聲，最小二乘法通過估計離散數據的趨勢變化函數去除信號中趨勢噪聲。由前述分析所知，在假定沖擊零漂誤差是由放大器輕度飽和引起的情況下，電荷放電服從指數曲線，可假設零漂誤差的趨勢函數為：

f(t)=a0e-a1t

(4)

利用最小二乘法對圖2所示沖擊信號去零漂后，可得到如圖3所示結果。

2.2 小波信號分離法

(5)

小波分離沖擊信號，必須針對信號特點選擇合適的小波基函數，實際應用表明，Db8適用于沖擊信號分析和處理，前7層作為重組信號，其它為零漂誤差項δ。修正后的信號如圖5所示。

2.3 EMD信號分離法

EMD計算過程是一個篩選迭代過程，這一篩選過程類似于濾波作用，按照時間尺度的局部特征分解出頻率高的IMF分量，而整個篩選過程會產生兩個效應：一是消除低頻載波；二是信號波形漸漸趨于對稱。這正是去除時域趨勢項所要求的結果。EMD方法是自適應的信號處理方法，具有很高的信噪比。

EMD方法的本質是通過特征時間尺度獲得本征模函數，然后由本征模函數分解數據序列。本征模函數IMF分量，必須滿足兩個條件：一是整個信號的局部極大值與局部極小值的數目之和和過零點的數目相等或最多相差一個；二是在任何一時間點上，由局部極大值所定義的上包絡線和極小值所定義的下包絡線的平均值為零。然而，信號一般是復雜信號，并不滿足IMF條件，可用經驗模態的方法將待分析信號分解為一系列表征時間尺度的IMF分量，其原理和步驟如下：

(1)找出原始信號xn,k(t)的極值點；

(2)利用3次樣條或Hermite多項式插值進行極值點擬合，找出局部極大值所定義的上包絡線un+1,k(t)與局部極小值所定義的下包絡線ln+1,k(t)；

(3)計算包絡線均值mm+1,k(t)=[un+1,k(t)+ln+1,k(t)]/2；

(4)取出分量hn+1,k(t)=xn,k(t)-mn+1,k(t)；

(5)重復步驟(1)～(4)，直到hn+1,k(t)滿足IMF的定義，記為in+1(t)=hn+1,k(t)；

(6)計算余量rn+1(t)=xn,0(t)-in+1(t)；

(7)如果rn+1(t)是一個趨勢分量，計算停止；否則重復步驟(1)～(4)找出其他的IMF分量。

采用EMD方法分離圖1所示沖擊信號，如圖6所示。

通過EMD方法分離了7個IMF分量，余量為零漂誤差量δ，7個IMF分量重組得到去除零漂后的沖擊信號，如圖7所示。

2.4 基于EMD的改進算法

由圖3、5、7中可以看出，最小二乘法、小波方法及EMD方法都很好地去除了信號零漂誤差，在時域上三者差異不大。圖8所示為3種方法修正后的沖擊響應譜。從圖8中可以看出，最小二乘、小波方法及EMD方法在頻域上的影響都超過1 000 Hz，達到了1 500 Hz左右。在高頻上，頻譜與原始信號頻譜也存在著差異，如圖9所示。

從圖9中可以看出，三者都很好的保留了信號頻譜峰值特征，在約2 000 Hz的拐點頻率以后，3種方法去零漂修正后信號的沖擊響應譜與原始信號沖擊響應譜誤差都不超過1dB，對于以沖擊響應譜進行環境復現試驗來說，3種信號處理方法都能夠很好的滿足要求。對于最小二乘法來說，需要一定的先驗信息，需要確定零漂的類型，如線性函數、指數函數、冪函數等，分析計算過程較為復雜，工程適用性較差。以小波信號分離方法去除零漂誤差，也需要先驗信息來確定小波函數和小波分析階數，分析階數的變化對結果影響極大。總體來說，最小二乘方法及小波信號分離方法，都需要在信號處理前進行先驗分析獲得先驗信息，才能獲得較好的結果。EMD方法具有較好的自適應性特性，在無任何先驗信息的基礎上使用EMD方法去除零漂誤差，均能得到較好的結果。

進行沖擊響應譜(頻域)模擬時，上述3種方法都較好的保留信號頻譜峰值特征，誤差也很小，處理后的信號均可以作為復現環境試驗的條件譜。但沖擊譜的低頻部分往往反映了結構大應變或位移，產生應力的也較大。而低頻段是難以確認信號是由結構本身響應引起的，還是零漂誤差造成。

隨著試驗技術手段的進步，利用電磁沖擊臺，對量級較小的瞬態沖擊，能夠較好地從時域上進行模擬。這就要求經過零漂處理后的信號，盡量能夠反映結構本身的響應特性。上述3種修正方法，在低頻段的損傷均較大。在EMD信號分離中，第1次分離出來的分量h(t)就包含了零漂誤差。那么針對h(t)進行處理就可快速得到零漂誤差。同時，繪制包絡線的過程，實質上是一個相對的低頻重采樣過程，會發生混疊現形象，是造成信號去零漂誤差后高頻段與原始信號偏離的主要原因。

單從除去零漂誤差來說，可以用下面修正算法：

(1)對原始信號xn,k(t)進行濾波，濾波頻率為采樣頻率1/2.56倍；

(2)找出原始信號xn,k(t)的極值點；

(3)利用3次樣條或Hermite多項式插值進行極值點擬合，找出局部極大值所定義的上包絡線un+1,k(t)與局部極小值所定義的下包絡線ln+1,k(t)；

(4)計算包絡線均值mm+1,k(t)=[un+1,k(t)+ln+1,k(t)]/2；

(5)取出分量hn+1,k(t)=xn,k(t)-mn+1,k(t)；

(6)計算余量rn+1(t)=xn,0(t)-hn+1,k(t)；

(7)余量rn+1(t)的沖擊響應譜滿足要求時，計算停止；否則重復步驟(1)～(6)找出合適的趨勢項。

這里，濾波要求不引起信號相位移動，否則在計算余量時會引入較大的誤差。因此，此處濾波采用傅立葉譜加頻域窗的方式進行率濾波。對信號進行FFT變換，對變換后數據如圖10所示的頻域窗，加窗后數據進行逆FFT變換得到濾波后數據。傅立葉譜加窗濾波后的信號與原信號不存在相位差，是零相位濾波。

基于這種修正算法的去零漂誤差處理后沖擊信號，如圖11所示，改進算法僅經過3次迭代運算即達到了要求，效率大大提高。

圖12～13所示為最小二乘法、小波方法、EMD方法和改進EMD方法修正后沖擊響應譜對比圖。從圖中可以看出，修正算法較好地保留低頻信號，700 Hz以后信號擬合度都較好，前述的3種方法，低于1 500 Hz的低頻信號削弱較大。另外，修正算法在高頻段基本與原信號完全重合，高頻信號基本無損傷。

4 結 論

本文中給出通過采集信號判斷放大器輕度飽和的原則，認為零漂具有電容放電特征；信號峰值不存在平頂小波現象。對比最小二乘法、小波信號分離法、EMD方法后發現，3種方法都能較好的去除零漂誤差，但低頻量削弱均較大。低頻量的削弱可能導致低頻模擬的失真，其可能剔除了結構本身的響應特征，不利于真實復現低量級爆炸沖擊環境。使用基于EMD的改進算法，可大大降低低頻信號的失真，高頻區域也可較好地保持原信號特征，完全滿足沖擊環境時域模擬的要求。同時，基于EMD的改進算法，計算效率相比其它算法具有高效的特點，同EMD算法一樣具有自適應性，適合工程上大數據量的處理，也盡可能保證了原始信號的有用信息。

參考文獻：

[1] 張國偉,馮順山,俞為民.高沖擊過載加速度傳感器零漂分析[J].華北工學院學報,2004,25(1):64-67.

ZHANG Guowei, FENG Shunshan, YU Weiming. Analysis of zero drift of the acceleration sensor in high impulsion and high overloading[J]. Journal of North China Institute of Technology, 2004,25(1):64-67.

[2] 夏偉強,馬鐵華,范錦彪,等.壓電式加速度計在高沖擊環境下的零漂分析[J].傳感技術學報,2007,20(7):1522-1527.

XIA Weiqiang, MA Tiehua, FAN Jinbiao, et al. Analysis of zero drift of the piezoelectric acceleration sensor in high impact testing [J]. Chinese Journal of Sensors and Actuators, 2007,20(7):1522-1527.

[3] 何宗穎,解鳳娟,郭旻,等.高能量沖擊條件下的加速度測試[J].火炮發射與控制學報,2011(1):85-88.

HE Zongying, XIE Fengjuan, GUO Min, et al. Acceleration measurement technology in high energy shock environment test [J]. Journal of Gun Launch & Control, 2011(1):85-88.

[4] 李海廣,潘宏俠,任海鋒.沖擊信號零漂修正的沖擊響應譜互相關系數分析[J].振動與沖擊,2016,35(16):219-225.

LI Haiguang, PAN Hongxie, REN Haifeng. Baseline correction of impact signals using the cross-correlation coefficient of shock response spectrum[J]. Journal of Vibration and Shock, 2016,35(16):219-225.

[5] 范錦彪,祖靜,徐鵬,等.彈丸侵徹混凝土目標減加速度信號的處理原則[J].探測與控制學報,2012,34(4):1-5.

FAN Jinbiao, ZU Jing, XU Peng, et al. Impact deceleration signal procession for concrete target penetration[J]. Journal of Detection & Control, 2012,34(4):1-5.

[6] 李曉強,李建剛,王繼紅,等.基于GJB150 艦船沖擊測量中零漂問題分析[J].環境技術,2016,34(5):75-78.

LI Xiaoqiang, LI Jiangang, WANG Jihong. Analysis on zero drift problem in ship shock measurement based on GJB150[J]. Environmental Technology, 2016,34(5):75-78.

[7] 龍源,謝全民,鐘明壽,等.爆破震動測試信號預處理分析中趨勢項去除方法研究[J].工程力學,2012,29(10):63-68.

LONG Yuan, XIE Quanmin, ZHONG Mingshou, et al. Research on trend removing methods in preprocessing analysis of blasting vibration monitoring signals[J]. Engineering Mechanics, 2012,29(10):63-68.

[8] 王錫雄,秦朝燁,丁繼鋒,等.基于離散小波分解的火工沖擊數據有效性分析與校正方法[J].振動與沖擊,2016,35(14):1-6.

WANG Xixiong, QIN Zhaoye, DING Jifeng, et al. Validation and correction of pyroshock data based on discrete wavelet decomposition[J]. Journal of Vibration and Shock, 2016,35(14):1-6.

[9] 王燕,薛云朝,馬鐵華.基于EMD和最小二乘法的零漂處理方法研究[J].北京理工大學學報,2015,35(2):118-122.

WANG Yan, XUE Yunchao, MA Tiehua. Research on zero drift processing method using EMD and Least-Square[J]. Transactions of Beijing Institute of Technology, 2015,35(2):118-122.

[10] 朱學鋒,韓寧. 基于經驗模態分解的非平穩信號趨勢項消除[J].飛行器測控學報,2012,31(1):65-70.

ZHU Xuefeng, HAN Ning. Removal of non-stationary signal trend items by empirical mode decomposition [J]. Journal of Spacecraft TT&C Technology, 2012,31(1):65-70.

[11] 謝全民,龍源,鐘明壽. 基于小波、小波包兩種方法的爆破振動信號對比分析[J].工程爆破,2009,15(1):5-9.

XIE Quanmin, LONG Yuan, ZHONG Mingshou. Comparative analysis of blasting vibration signal based on wavelet and wavelet packets transform[J]. Engineering Blasting, 2009,15(1):5-9.