級數一致收斂的狄利克雷判別法的相關結論研究
丁 慧 崔國范 王鳳玲
(綏化學院信息工程學院 黑龍江綏化 152061;2.黑河學院 黑龍江黑河 164300)
數學分析是數學專業的基礎課程,其中判斷函數項級數的一致斂散性是一重點及難點問題,其中判別級數收斂的方法很多,如何能深入系統地把握各種方法間的關系,運用判別法靈活、快捷地解決問題是我們積極探索的問題。
一、判別函數項級數一致收斂的方法
判別函數項級數一致收斂的方法有柯西一致收斂原理,M判別法,阿貝爾及狄利克雷判別法等,他們的具體內容如下:
引理1[1](Cauchy一致收斂原理)級數在D一致收斂的充要條件為:?ε>0,?N,當 n>N,?p∈N,?x∈D,有
引理2[2](M判別法)設級數un(x)定義在區間D上,是收斂的正項級數。若當n充分大時,對?x∈D,有則在D上一致收斂。
對于此定理要注意,若級數在區間D上不存在優級數,則不能推出級數在區間D上非一致收斂.
引理3[1](Abel判別法)設級數滿足:
(2)對每個x∈D,數列{vn(x)}單調,且函數列{vn(x)}在D上一致有界,即?M>0,使對于?x∈D,?n,有 |vn(x)|≤M,則級數在區間D上一致收斂。
引理4[2](Dirichlet判別法)設級數滿足:
(1)級數的部分和函數列在區間D上一致有界;
(2)對于每一個D,數列{vn(x)}單調且在區間D上函數列{vn(x)}一致收斂于零,則級數在區間D上一致收斂。
二、研究結果
凡凡種種的數學分析教材都能指出狄利克雷判別法包含了阿貝爾判別法,狄利克雷判別法還包含了交錯級數的萊布尼茲判別法,我們將給出狄利克雷判別法也包含了一致柯西收斂原理,狄利克雷判別法的推廣到復數域的形式以及與其他判別法的系統關系圖。
(一)狄利克雷判別法包含一致柯西收斂原理。
定理1 若級數滿足狄利克雷判別法,則級數滿足一致柯西收斂原理。
證明:因為部分和函數列有界,則max{|vk(x)|,|vm(x)}|是有界的,即
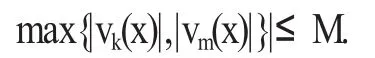
同時,由于級數一致收斂,根據柯西收斂原理,對于任意的ε>0,對于足夠大n和k>n,以及任何x∈E,有
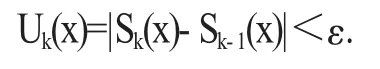
又因為不等式
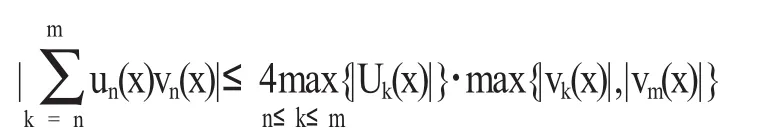
于是,級數滿足一致柯西收斂原理。
(二)狄利克雷判別法推廣形式。函數項級數一致收斂的狄利克雷判別法不僅在實數域上成立,而且可以推廣到復數域上,推廣形式如下:
定理 2[3]設 E?X,un:X→C,其中 C是復函數,vn:X→R,其中R是實函數,級數滿足:
(1)級數的部分和在E上一致有界;
則級數在E?X上一致收斂。
由這個定理我們給出為數項級數時,并將條件{vn}弱化為{vn},其修正后是單調的,且構成絕對收斂級數。
定理3 設E?X,un:X→C,其中C是復數,vn:X→R,其中R是實數,級數滿足:
(1)級數的部分和在E上有界;
(2){γn}在 E單調,且構成絕對收斂級數;則級數在E上收斂。
證明:級數的部分和在E上有界,即存在M>0,使得(不依賴于的常數),則在E上,?p>0,恒有
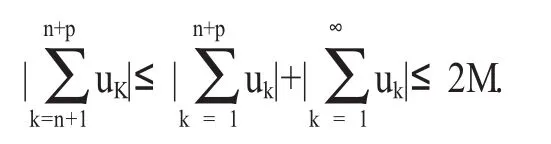
{γn}在 E 構成絕對收斂級數,則滿足?ε>0,?N,當 n>N,?p∈N,有ε,進而有
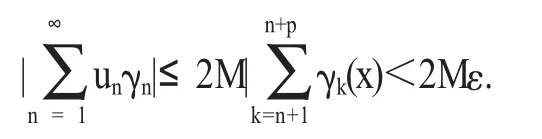
所以級數在E上收斂。
(三)狄利克雷判別法與其他一致收斂判別法的關系圖。

函數項級數一致收斂的狄利克雷判別法包含阿貝爾判別法、柯西收斂原理,同時它也可以推廣到對于任意點集的復數域上函數項級數,其中點集可以是有限區間,也可以是無限區間.狄利克雷判別法不僅可以特殊化為交錯級數的萊布尼茨判別法,而且可以將數項級數條件弱化為{vn},當修正后是單調的,且構成絕對收斂級數.
三、結束語
從對于函數項級數一致收斂的狄利克雷判別法入手,詳細地論證出了狄利克雷判別法與其它判別法間的關系,展現了知識間的系統聯系性.同時,給出狄利克雷判別法的推廣及弱化的數項級數的斂散條件,使解決的對象外延擴大,而且便捷有效地解決函數項的一致收斂這一難點問題.
參考文獻:
[1]歐陽光中,朱學炎,金福臨,等.數學分析(下)[M].高等教育出版社2015:75-88.
[2]劉玉蓮.數學分析(下)[M].北京:高等教育出版社,2010:70-75.
[3]B.A卓里奇.數學分析[M].北京:高等教育出版社,2008:330-333.
[4]謝惠民,沐定夷.吉米多維奇數學分析習題集學習指引[M].北京:高等教育出版社,2013:144-145.
[5]文德祥,劉紹武,馮立新.北京大學出版社[M].北京:北京大學出版社,2014:72-75.

