《機器學習》課程教學案例
——手寫數字識別系統開發

米吉提·阿不里米提，吾米提·尤努斯，艾斯卡爾·艾木都拉

（新疆大學信息科學與工程學院，烏魯木齊 830046）

0 引言

人工智能、機器人、大數據等已經離不開我們的生活。教育部發文，機器人與編程被列入2018高中必修課。機器人素質教育進入校園，其核心概念是機器學習。機器學習在諸多領域成功的應用與發展，己成為信息處理領域的基礎和熱點[1-2]。機器學習的相關的課程從研究生教育逐漸進入高中教育階段。作為一門實踐性極強的課程，其內容自然聯系到諸多抽象概念和基礎課程。雖然，機器學習相關的教學課程及網上課堂很多[3]，內容也豐富多樣，但缺乏簡單易懂的案例教學。將復雜的內容有效教授給學生、以及讓學生掌握其精粹、理解其內涵是件艱巨的任務。通過案例場景引出相關概念、技術，以此為主線增強學生的學習信心可能是機器學習課程最有效的教學方法。一個具體案例能有效掌握主題、消除疑惑、理解抽象概念等方面取到舉一反三的目標[4]。

從多年的教學工作當中發現，大部分教材及參考書，注重抽象概念及普遍理論的講解。對于具體簡單的例子的講解案例嚴重缺乏。導致學習過程只是現成工具的套用，最終對抽象概念一知半解，越學越覺得吃力、脫離實踐、死記硬背。學習效率差，直接導致厭學。甚至有的學生直接提出“既然有很好的現成工具就不需要學習，直接應用即可”。

機器學習方法之多，如 HMM、GMM、K-means、SVM、DNN等，內容之抽象，很容易導致理論脫離實踐。本文采用比較直觀的例子“手寫數字的識別”作為例子講解一個以線性分類器為核心的機器學習方法。多維線性函數是SVM、DNN等效果比較好的機器學方法的基礎，直觀并易于理解、容易實現。對于初學者是個理想的實踐過程。

1 模型的建立

機器學習的目標可以是各種信息，包括視覺信號及聽覺信號等。比較典型的是語音及文字信息。其中文字圖像比較直觀，用于機器學習教學效果更好。但是手寫數字包含隨機變化成分，因為我們知道每個人書寫方式、習慣、大小、角度等不會完全一樣，相同的數字一個人寫兩次也不會完全一樣。但是每個文字或數字都有固定的模版。我們可以用模版的匹配度量來區分不同數字或進行分類。因此，即需要很好的機器學習模型，有需要大量樣本的訓練過程。

可以用較復雜的概率統計概念來設計一個模型[3]，也可以用簡單的線性函數來實現分類過程。機器學習模型需要在訓練樣本中訓練。類似于，一個小孩開始學習認知數字。先讓孩子學習各個數字，然后讓其辨認一些數字。剛開始，孩子雖然能正確辨認出比較規整的手寫數字，也會誤判一些寫的較潦草的數字。慢慢通過學習（學習各種手寫樣本）就能不斷提高準確率。

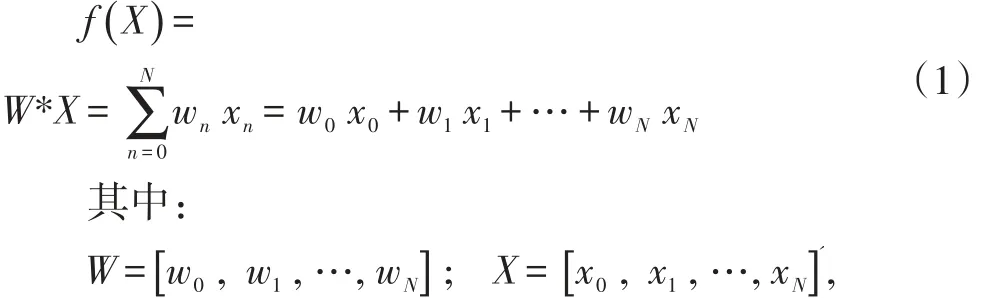
機器學習過程需要模型和樣本兩部分，首先設計一個數學模型，其次在大量樣本上學習后調整模型的參數，并用該模型去判斷新的手寫數字。公式（1）一個線性模型，是另外兩個重要機器學習模型的基礎，深度神經網絡（DNN）和支持向量機（SVM）。

設x0=1

公式（2）計算結果是對某個樣本數字的特征向量X的預測值。機器學習的目的是提高該預測的正確率。這里要訓練的模型參數是W=[ ]w0,w1,…,wN。

圖1 單個線性分類器模型

輸入一系列樣本數據X(1),X(2),X(3),…我們的訓練目標是找到合適的參數W使得若（2）大于零則正確，小于零則錯誤。這是一個簡單的2類分類技術，即只能用于一個數字的辨認。

訓練過程是一個循序漸進過程。先W給指定一個初始值，然后根據對樣本的識別結果進行調整。若有10個訓練樣本X(1),X(2),X(3),…,X(10)對應于0到9十個數字。模型的訓練目標是[…y(k)…] =[-1,…,-1,1,-1..]，對應數字“3”時y(k)=1，其他都等于-1。假設，我們通過公式（2）計算出來的結果是“全部大于零”，則錯誤率是90%，若“全部小于零”，則錯誤率是10%。因為我們的目標是正確識別數字“3”。只有測試“3”時f(X)結果大于零，其他樣本時小于零才是正確的結果。即，正確識別結果應該是sign(f(X))=[-1,-1,-1,1,-1,…,-1]。

循序漸進的方法是先設置多次循環，每次循環給所有參數[w0,w1,…,wN]進行調整，最終獲得最佳參數W。每次對參數的微調方式是公式（3）

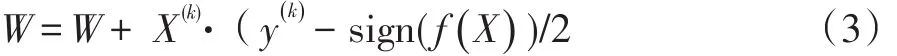
其中，（y(k)-sign(f()X)決定調整的方向。若預測值和實際值相同則沒必要調整，否則向y(k)的方向進行調整。X(k)是調整的幅度，是線性函數的偏微分。

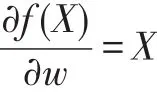
雖然該例子很簡單，但是任何復雜的機器學習模型都是通過對公式（1）～（3）的改變或優化獲得的，機器學習的核心思路沒變。若將公式（2）換成公式（4），模型就變成了標準的感知器（perceptron）模型。圖1顯示的是一個數據（如：數據“3”）的預測模型，10個這樣的模型并聯成起來就成了識別10個數據的單層原始神經網絡模型。

2 試驗數據準備

圖像在計算機中的簡單（單色）表示方法是矩陣形式，如圖2。這些信號輸入機器學習模型時，需要轉換成一系列特征向量。特征向量可能是一維的，也可能是二維的。相應的特征數據有有統計特征、鉅、方向特征等等，也可能是圖像矩陣本身。

在監督機制建設中要重點強化企業的成本監督和相關管理工作，要以成本作為監督的目標，理順企業生產、管理的經濟關系，從成本控制的角度構建起有針對性、可執行的監督平臺和監督制度，真正將監督工作的重點放在對企業各項成本的控制工作上，提升企業成本管理、運營管理的效率，打造企業在生產、管理和經營上的經濟、組織與成本優勢。

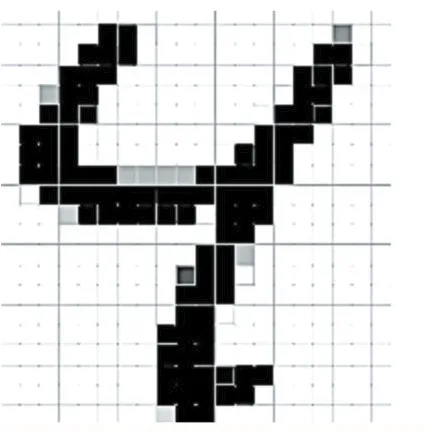
圖2 手寫數字矩陣實例

數據準備過程需要圖像的采集、二值化、規范化、細化等過程。最終獲得大小規整的數字矩陣。圖2顯示一個數字矩陣，白色用0表示，黑色用1表示，就能獲得2維矩陣。

大家可以自己找幾個人進行手寫數字的采樣和預處理過程。也可以直接用免費數據MNIST[5]，MNIST提供了6萬個訓練樣本，和1萬個測試樣本，每個樣本是一個28×28矩陣。收集樣本時要注意，訓練樣本和測試樣本是不同人提供的。

由于我們用的線性模型是一維向量模型，所以需要對二維向量進行降維、或直接將矩陣逐行拼接成一維向量。所有樣本X(1),X(2),X(3),…,X(N)和對應的正確數字標注[y(1),y(2),y(3),…,y(N)]交給模型。X(i)是個一定長度（28×28）的向量，y(i)是對應的標注信息，-1或 1，例如模型的目的是識別數字“3”則對應“3”的標注是1，其他都是-1。訓練結束后，在獨立的測試樣本上進行測試并獲得試驗結果。

3 實現過程

模型實現方法比較簡單，大家可以用任何編程語言，如：Python，C，MATLAB等，實現。如下我們提供的偽代碼。其中X是所有訓練數據，每行是一個樣本，總行數M是總樣本數，列數是一維特征向量，長度為N，注意x0=1，即將矩陣X的第一列全設置成1，對應的參數w0成為偏移量。實際信號的特征值長度是N-1。Function Linear_model（X,Y） {

[M,N]=size（X） #獲得樣本數M，和向量長度N

W=ones（N） #參數初始化成全1的向量

err=0 #錯誤率,初始化

while（err＞0.1） #err是錯誤率。或者可以循環100次

{

for i=1：M #循環計算每個樣本的預測值，并對參數更新

{

Fx=sign（W*X[i,：]） # 注意矢量相乘，X[i,：]需要轉值

W=W+X[i,：]·（Y[i]-Fx）# 更新參數

err=err+（Y[i]-Fx）/2 #錯誤累加

}

err=err/M #錯誤率

}

return W }

我們取了20個人的200個樣本數據進行訓練，并在少量測試數據上進行測試，錯誤率為22%。這只是一個數字的識別過程，要實現10個手寫數字的識別模型，簡單的并聯即可。

4 結語

《機器學習》作為一門實踐性極強的課程，其內容自然和諸多抽象概念和基礎課程有關。將這些內容有效教授給學生，以及讓學生掌握其精粹、理解其內涵是件艱巨的任務。本文以教學為目的介紹了一個簡單且典型的機器學習模型機器設計和訓練過程。雖然關于機器學習的書籍及參考資料很多，對于初學者的簡單案例教學形式的材料嚴重缺乏。因此，盡量用通俗易懂的方式講解了機器學習完整過程，避免了概念的抽象化，注重具體細節和實現過程。難免有不足之處，希望大家批評指正。

參考文獻：

[1]余明華，馮翔，祝智庭.人工智能視域下機器學習的教育應用與創新探索.遠程教育雜志，2017-05-20.

[2]鄧志鴻，謝昆青.機器學習課程的教學實踐——以北京大學“智能科學與技術”本科專業為例.計算機教育，2016-10-10.

[3]Christopher Bishop.“Pattern Recognition and Machine Learning”.Springer press,2007.

[4]李勇.本科機器學習課程教改實踐與探索.計算機教育，2015-07-10.

[5]http：//yann.lecun.com/exdb/mnist/.