本量利之不確定條件下的利潤預(yù)測

趙麗娜 張霞麗

[摘 要]傳統(tǒng)本量利分析假設(shè)企業(yè)的單價、固定成本總額、單位變動成本是固定不變的，但企業(yè)實(shí)際經(jīng)營管理環(huán)境對這些因素的預(yù)計或多或少總會帶有不確定性。財務(wù)人員需要正確把握成本性態(tài)，掌握市場需求動向，探究企業(yè)經(jīng)營管理中存在的不確定性，運(yùn)用概率分析方法可以提高利潤預(yù)測結(jié)果的可靠性。

[關(guān)鍵詞]本量利；利潤預(yù)測；概率模型

[中圖分類號]G239.2-F [文獻(xiàn)標(biāo)識碼]A

1 傳統(tǒng)本量利分析

本量利分析指對利潤、成本和業(yè)務(wù)量之間關(guān)系進(jìn)行分析的簡稱，是在成本性態(tài)和變動成本法基礎(chǔ)上的管理會計分析方法。

本量利分析在企業(yè)預(yù)測、決策、計劃和控制等方面有廣泛的用途，其核心是確定“盈虧平衡點(diǎn)”。其基本公式為：

利潤=單價×銷售量-單位變動成本×銷售量-固定成本

傳統(tǒng)的本量利分析方法是一個理想化的模型，基本假設(shè)為：

（1）變動成本與業(yè)務(wù)量為完全線性關(guān)系假設(shè)；（2）固定成本保持不變假設(shè)；（3）產(chǎn)銷均衡假設(shè)；（4）銷售收入與銷售數(shù)量為完全線性關(guān)系假設(shè)；（5）品種結(jié)構(gòu)不變假設(shè)。總之，假設(shè)企業(yè)處于一種成本、利潤和業(yè)務(wù)量之間呈完全的線性關(guān)系的經(jīng)營環(huán)境中。

傳統(tǒng)的本量利分析在這些理想的假設(shè)條件下，利潤的預(yù)測很容易計算，不存在不確定性。但傳統(tǒng)的本量利分析的假設(shè)條件一般不符合現(xiàn)實(shí)，現(xiàn)實(shí)經(jīng)濟(jì)生活中，情況錯綜復(fù)雜，未來充滿著未知。因此本文主要針對不確定條件下的本量利分析加以分析探討。

2 不確定條件下的本量利分析

在經(jīng)濟(jì)活動中，某一事件在同樣條件下可能發(fā)生，也可能不發(fā)生，這類事件為隨機(jī)事件，而概率是用來表示隨機(jī)事件發(fā)生可能性大小的數(shù)值，其取值范圍在0-1之間。在本量利分析中，單價、單位變動成本、固定成本和銷售量都可能成為不確定性因素。本文假定單價、單位變動成本、固定成本和銷售量都為隨機(jī)變量，進(jìn)行本量利分析。

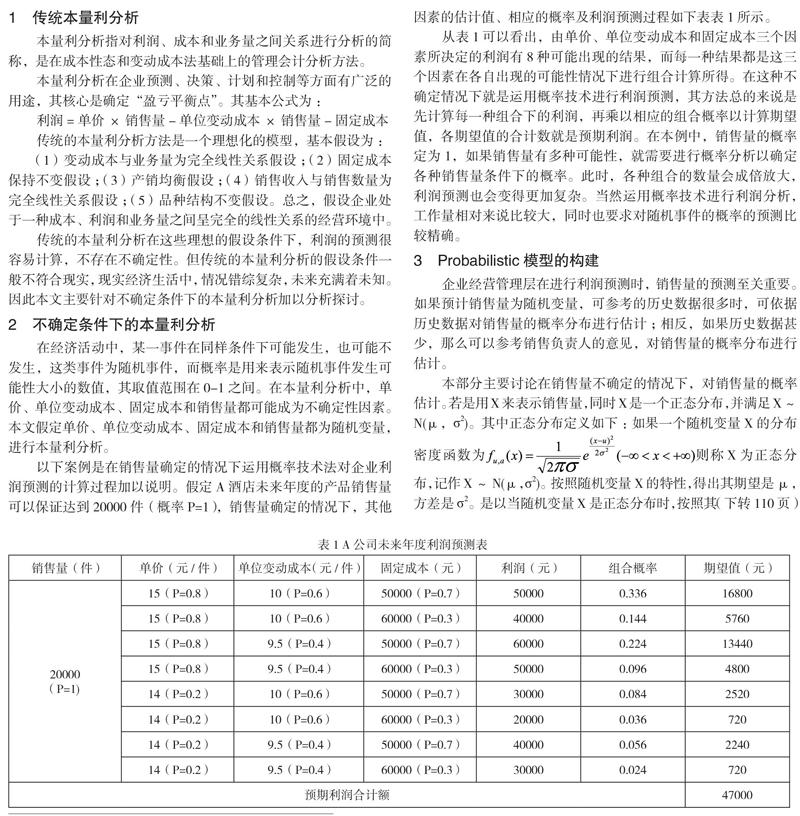
以下案例是在銷售量確定的情況下運(yùn)用概率技術(shù)法對企業(yè)利潤預(yù)測的計算過程加以說明。假定A酒店未來年度的產(chǎn)品銷售量可以保證達(dá)到20000件（概率P=1），銷售量確定的情況下，其他因素的估計值、相應(yīng)的概率及利潤預(yù)測過程如下表表1所示。

從表1可以看出，由單價、單位變動成本和固定成本三個因素所決定的利潤有8種可能出現(xiàn)的結(jié)果，而每一種結(jié)果都是這三個因素在各自出現(xiàn)的可能性情況下進(jìn)行組合計算所得。在這種不確定情況下就是運(yùn)用概率技術(shù)進(jìn)行利潤預(yù)測，其方法總的來說是先計算每一種組合下的利潤，再乘以相應(yīng)的組合概率以計算期望值，各期望值的合計數(shù)就是預(yù)期利潤。在本例中，銷售量的概率定為1，如果銷售量有多種可能性，就需要進(jìn)行概率分析以確定各種銷售量條件下的概率。此時，各種組合的數(shù)量會成倍放大，利潤預(yù)測也會變得更加復(fù)雜。當(dāng)然運(yùn)用概率技術(shù)進(jìn)行利潤分析，工作量相對來說比較大，同時也要求對隨機(jī)事件的概率的預(yù)測比較精確。

3 Probabilistic模型的構(gòu)建

企業(yè)經(jīng)營管理層在進(jìn)行利潤預(yù)測時，銷售量的預(yù)測至關(guān)重要。如果預(yù)計銷售量為隨機(jī)變量，可參考的歷史數(shù)據(jù)很多時，可依據(jù)歷史數(shù)據(jù)對銷售量的概率分布進(jìn)行估計；相反，如果歷史數(shù)據(jù)甚少，那么可以參考銷售負(fù)責(zé)人的意見，對銷售量的概率分布進(jìn)行估計。

本部分主要討論在銷售量不確定的情況下，對銷售量的概率估計。若是用X來表示銷售量，同時X是一個正態(tài)分布，并滿足X～ N（μ，σ2）。其中正態(tài)分布定義如下：如果一個隨機(jī)變量X的分布密度函數(shù)為則稱X為正態(tài)分布，記作X～ N（μ，σ2）。按照隨機(jī)變量X的特性，得出其期望是μ，方差是σ2。是以當(dāng)隨機(jī)變量X是正態(tài)分布時，按照其期望或方差，X的分布函數(shù)也能確定下來。本節(jié)后半部分主要來計算銷售量X的期望與方差的值。

利用抽樣調(diào)查，針對服從正態(tài)分布的母體，我們可以取得子樣的n個觀測值，如最近n年的銷售量X1，X2，X3，… ，Xn。

在統(tǒng)計學(xué)中可以利用這n個觀測值并采用極大似然估計方法來估計母體的期望μ與方差σ2 。極大似然估計過程如下所示：

正態(tài)分布的似然函數(shù)如下所示：

利用統(tǒng)計學(xué)中參數(shù)檢驗(yàn)的方法，驗(yàn)證期望μ=u與方差σ2=σ2估計的可靠性。先設(shè)定顯著性水平為α，且α=0. 05，構(gòu)造兩個統(tǒng)計量 與 其中 ，χ2（n-1）表示自由度為n- 1的卡方分布，t（n- 1）表示自由度為n- 1的t分布，。通過以上計算和驗(yàn)證，本文取得了銷售量X所服從的正態(tài)分布。

在實(shí)際工作中，如果所研究的公司是剛剛起步的創(chuàng)業(yè)公司，我們會無法取得多年銷售量數(shù)據(jù)的具體情況，只能獲取近一兩年的數(shù)據(jù)。而獲得的數(shù)據(jù)涉及的年份越少，我們估計出的結(jié)果就越不精確，此時，我們也只能根據(jù)經(jīng)驗(yàn)作出粗略的估計。例如在A酒店銷售數(shù)據(jù)較少的情況下確定μ時，如果A酒店225間房的使用比率達(dá)到60%，那么μ= 0. 6×225× 365= 49275，從而利用以下估計式p（- 2000< X- 49275< 2000）= 0. 5來估出σ2的值。

我們在實(shí)際工作中遇到的許多變量其實(shí)都適用于統(tǒng)計學(xué)中的中心極限定理，那些變量一般呈正態(tài)分布或近似地服從正態(tài)分布，因此在例題中假定銷售量概率分布為正態(tài)分布是符合實(shí)際情況的。此外，不但本量利分析中的銷售量可作為隨機(jī)變量，單價、單位變動成本和固定成本也可設(shè)定為隨機(jī)變量，并可以運(yùn)用概率論的原理和方法進(jìn)行分析。從本文的分析可以看出，管理人員要應(yīng)對變化莫測的市場變化，就需要努力掌握市場需求變動方向，正確把握成本性態(tài)，盡可能利用相關(guān)學(xué)科的知識和分析方法，計算出最接近企業(yè)客觀情況的預(yù)期利潤，從會計的角度提供促使決策最優(yōu)化的信息。

[參考文獻(xiàn)]

[1] 溫素彬，張自東.管理會計工具及應(yīng)用案例——本量利分析模型的決策指標(biāo)及應(yīng)用[J].會計之友，2016（06）.

[2] 溫素彬.管理會計中Excel的高級應(yīng)用——隨機(jī)條件下的本量利分析模型設(shè)計與應(yīng)用（Ⅱ）[J].財務(wù)與會計，2014（04）.