基于軸箱彈簧故障狀態的鐵路客車動力學性能分析

楊亮亮， 馮遵委， 楚永萍， 賈小平， 黃曉翠

(中車南京浦鎮車輛有限公司 技術中心， 南京 210031)

軸箱彈簧是連接構架與軸箱的主要彈性元件，起著隔離輪軌高頻沖擊和緩和構架隨機振動的作用，并使車體和構架的質量能比較均衡地傳遞給各輪軸。隨著車輛的長期服役，除了線路不平順的激擾外，鋼軌和車輪的磨耗、剝離和擦傷等現象將進一步惡化軸箱彈簧的受力狀態，從而彈簧疲勞斷裂的情況時有發生。

當軸箱彈簧出現斷裂后，其剛度將發生變化，車體和構架等將發生微小傾斜，并引起整個車輛載重的重新分配，各車輪靜重將不再保持均衡，這將給車輛運行安全帶來一定程度的隱患。Priyanka等[1]采用ADAMS/Rail軟件分析了貨運機車軸箱彈簧失效后的車輛運行平穩性；Kumar等[2]采用ANSYS軟件分析了機車軸箱彈簧在可能發生故障前的安全載荷；劉國云等[3]采用SIMPACK軟件分析了高速列車軸箱彈簧全拆狀態和低溫“凍死”狀態下的車輛動力學性能；劉麗等[4]采用SIMPACK軟件分析了動車組軸箱彈簧斷裂過程中的車輛動力學性能。上述研究中對軸箱彈簧故障狀態的建模多以極端情況為主，而實際軸箱彈簧斷裂情況往往并非那么嚴重。

因此，以實際故障統計情況為依據，建立軸箱彈簧發生斷裂后處于斷裂接觸和斷裂失效的兩種理論力學模型，并對6種軸箱彈簧故障狀態開展車輛動力學仿真分析。

1 軸箱彈簧故障狀態力學模型

一般而言，轉向架的軸箱彈簧主體部分主要包括內側圓鋼簧、外側圓鋼簧、橡膠墊、構架端彈簧座、軸箱端彈簧座、構架端止擋銷、軸箱端止擋銷等，如圖1所示。

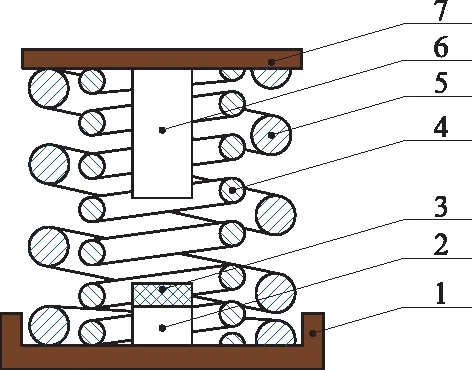
1-軸箱端彈簧座；2-構架端止擋銷； 3-橡膠墊；4-內鋼簧；5-外鋼簧； 6-構架端止擋銷；7-構架端彈簧座。圖1 軸箱彈簧組成

由統計2014～2015年某客車車輛在7個客車車輛段內的48起軸箱彈簧折損信息[5]可知，發生斷裂行為后的故障狀態主要有兩種。一種是軸箱鋼彈簧在車輛運行過程中發生斷裂后形成上、下兩段斷簧，但均沒有脫落，在相當長的時間內保持這兩段斷簧相互接觸并串聯在一起繼續起支撐和緩沖作用，其占比約為98%。另一種是軸箱鋼彈簧在車輛運行過程中發生斷裂后形成上、下兩段斷簧，但斷簧又部分或全部脫落，部分脫落時相當于剩余彈簧起支撐和緩沖作用，完全脫落時相當于軸箱與構架之間的橡膠止擋起支撐和緩沖作用，其占比約為2%。此外，內簧和外簧發生斷裂的比例分別為12%和88%，斷口均出現在靠近端圈1～2圈附近的工作圈處，但沒有出現內、外簧均發生斷裂的情況，且斷簧所在轉向架的具體位置并無明顯規律。

若忽略彈簧在斷裂瞬間的狀態變化，僅以已形成斷簧后的故障狀態為準，從彈簧剛度和高度的變化以及斷簧狀態的角度出發，建立了兩種典型軸箱彈簧故障狀態的力學模型，即斷裂接觸模型和斷裂失效模型。

1.1 斷裂接觸模型

彈簧斷裂后繼續維持接觸狀態，但斷口附近的原工作彈簧并不能像兩端的支持彈簧那樣有切削支撐平面來輔助彈簧均勻、穩定地傳遞載荷，實際斷裂后形成的兩段斷簧之間接觸的部位和狀態往往都是隨機的。為了便于分析，假設彈簧斷裂后形成的兩段斷簧能夠均勻、穩定地相互接觸，且接觸面始終處于水平狀態，此時接觸區域可視為僅起支撐作用的彈簧部分，原彈簧的正常工作狀態在斷裂后形成兩段斷簧串聯的亞工作狀態，如圖2所示。

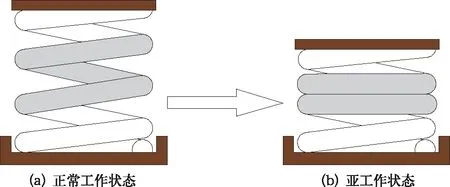
圖2 斷裂接觸模型

由彈簧串聯特性可知，斷裂前、后彈簧的軸向剛度[6]可表示為

(1)

圖3 斷簧的壓磨痕跡

若以僅外簧斷裂情況為例，則斷裂接觸模型下的彈簧垂向載荷與撓度之間的關系可表示為

(2)

式中Fz為彈簧垂向載荷；z為彈簧撓度；n1、n2分別為原內、外簧的總圈數；k1z、k2z分別為原內、外簧的垂向剛度；H0為內、外簧的自由高度，這里取兩者相同的情況；nJ為兩斷簧相互接觸的圈數。

此外，從圖3中的壓磨痕跡可以推知斷簧接觸部位沿水平方向發生過不同程度的相對摩擦運動。為了便于分析，可假設摩擦面是連續且固定的，并采用圖4中所示的黏滑摩擦模型來模擬兩段斷簧的橫向受力關系，即

(3)

式中Fxy為彈簧橫向載荷；Fn為兩段斷簧接觸部位的支撐壓力，若不考慮彈簧自身慣性因素，可認為Fn=Fz；vij為兩段斷簧的橫向相對速度；rij為兩段斷簧的橫向變形量之和；μstick為兩段斷簧接觸部位的靜摩擦系數；μslip為兩段斷簧接觸部位的滑動摩擦系數；ev為黏著與滑動狀態轉化速度；kxy和cxy分別為兩段斷簧串聯后的橫向剛度和阻尼。

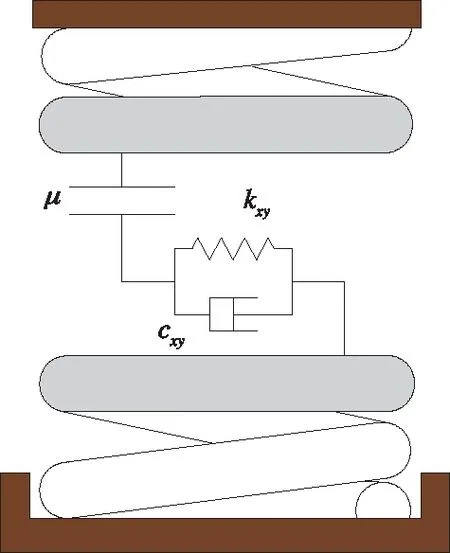
圖4 斷簧的黏滑摩擦模型

1.2 斷裂失效模型

彈簧斷裂后形成的斷簧發生了脫落丟失或工作失效的現象，由于軸箱端彈簧座為環包式結構，因此上段斷簧比下段斷簧更容易發生丟失或失效。一般情況下，軸箱彈簧主要為兩卷圓鋼簧并聯組成，因此根據彈簧失效程度可分為部分失效狀態和全部失效狀態，如圖5所示。

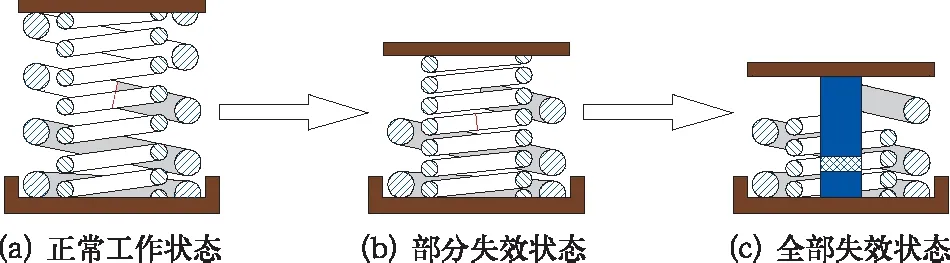
圖5 斷裂失效模型

若僅以外簧斷裂情況為例，整個軸箱彈簧故障狀態可等效為如圖5(b)所示的斷裂失效模型，則外簧斷裂失效后的彈簧垂向載荷與撓度之間的關系可表示為

(4)

式中nT為上段斷簧的總圈數，即彈簧斷裂后脫落失效的圈數；nJ為下斷簧上部與構架端彈簧座相互接觸的圈數。

若故障狀態處于如圖5(c)所示的極端情況下，即內、外簧均發生斷裂失效，則此狀態下的彈簧垂向載荷與撓度之間的關系可表示為

Fz=kstopz

(5)

式中kstop為垂向止擋剛度。

此外，軸箱彈簧高度的損失不僅會引起彈簧軸向剛度的變化，也會導致彈簧橫向剛度的變化，這里采用螺旋圓鋼簧剛度比的近似算法[7]進行折算，即

(6)

式中khorizontal為彈簧的水平剛度；λ為長細比，即H0/D；

ζ為相對撓度，即z/H0；E為彈性模量。

2 軸箱彈簧故障狀態仿真分析

為了研究軸箱彈簧故障狀態下的車輛運行性能，以某鐵路客車車輛為研究對象，其轉向架采用轉臂式定位，一系懸掛由軸箱彈簧和垂向液壓減振器組成，二系懸掛包括空氣彈簧、橫向液壓減振器、垂向液壓減振器、抗蛇行減振器和抗側滾扭桿等。其中，軸箱彈簧采用單組雙卷螺旋圓鋼簧的承載模式，其基本參數如表1所示。

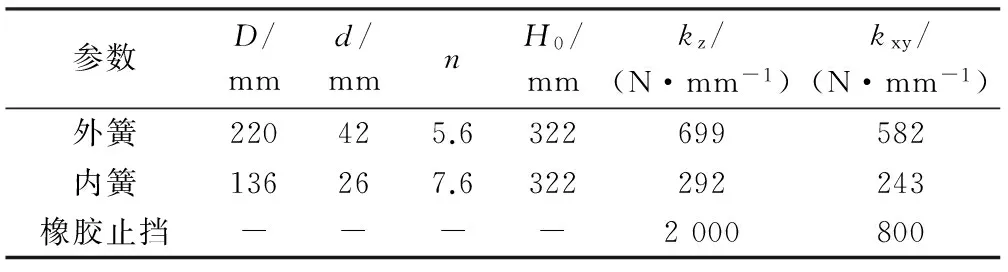
表1 軸箱彈簧基本參數

在故障狀態模擬中，僅考慮前轉向架一位輪對左側車輪處的軸箱彈簧發生斷裂，其他位置的軸箱彈簧均正常，且斷裂位置選取靠近軸箱端彈簧座的1/3彈簧長度處，該位置也是鐵路車輛軸箱彈簧實際斷裂最頻繁的。若假設軸箱彈簧斷裂后僅發生垂直坐落且不考慮構架結構自身的扭轉剛度影響，可根據力的平衡條件得到理想情況下軸箱彈簧故障前后的轉向架一系受力狀態，如圖6所示。其中，P為正常工況下構架在軸箱處的垂向支撐力；ΔP為由于彈簧故障引起的構架在故障軸箱處損失的垂向支撐力。

圖6 構架4個軸箱處的受力狀態

根據車輛系統動力學理論[8]建立了該鐵路客車車輛的仿真模型。在該模型中車輛由1個車體、2個構架、8個軸箱和4個輪對組成，輪軌匹配采用基于跡線法的接觸幾何關系，非線性蠕滑力采用基于Kalker簡化理論的FASTSIM算法進行計算。為了便于比較分析，考慮了7種不同的軸箱彈簧工作狀態，如表2所示。

表2 軸箱彈簧工作狀態

以故障軸箱側的轉向架和車體為計算輸出項，仿真得到車輛分別以160，125，97，69 km/h的速度通過直線、大半徑(R1 000 m)曲線、中等半徑(R600 m)曲線和小曲線(R300 m)半徑時的輪軸橫向力、脫軌系數、輪重減載率、構架振動加速度、車體平穩性指數等指標，如圖7～11所示。

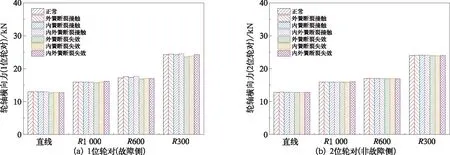
圖7 輪軸橫向力

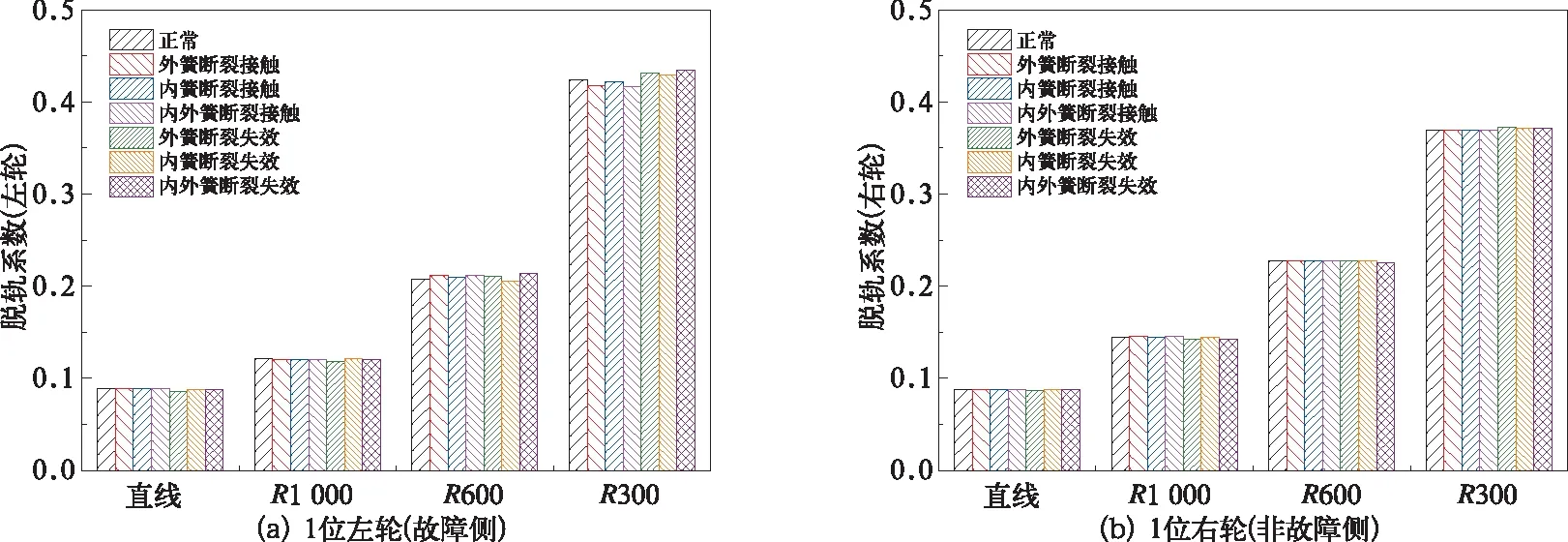
圖8 脫軌系數

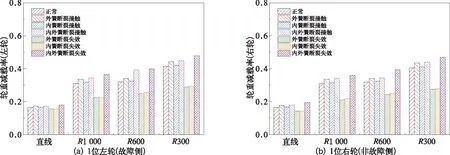
圖9 輪重減載率

由圖7～圖9中的仿真結果可知，不同軸箱彈簧故障狀態下引起的輪軌安全性指標具有明顯的差異。具體來說，軸箱彈簧故障對輪軸橫向力和脫軌系數指標的影響較小，與正常工況相比，該兩個指標值分別增大3%和4%，且僅表現在故障側輪軸處，非故障側輪軸處幾乎無影響。而軸箱彈簧故障對輪重減載率指標的影響較大，且不僅表現在故障側車輪處，也表現在非故障側車輪處，其中危險系數最大的故障類型依次為內外簧全部斷裂失效工況、內外簧全部斷裂但仍接觸工況和外簧斷裂但仍接觸工況，與正常工況相比，其輪重減載率指標值分別增大14%、9%和7%，這說明由于局部軸箱彈簧垂向剛度的增加將一定程度地降低車輛運行安全性。

此外，軸箱彈簧故障對構架和車體的振動傳遞也具有一定的影響。由圖10可知，軸箱彈簧故障狀態中，外簧斷裂失效工況下引起的構架橫向振動最劇烈，此時軸箱彈簧的橫向緩沖能力最弱，與正常工況相比，構架橫向振動加速度增大5%；而內外簧全部斷裂但仍接觸工況下引起的構架垂向振動最劇烈，此時軸箱彈簧的垂向剛度較大且橫向約束也較大，與正常工況相比，構架垂向振動加速度增大12%。由圖11可知，由于空氣彈簧良好的隔振能力，軸箱彈簧故障對車體平穩性的影響有限，且僅表現在垂向，橫向幾乎不變。

圖10 構架振動加速度

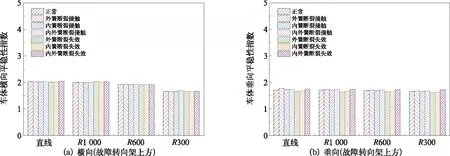
圖11 車體平穩性指數

3 結 論

(1)通過調研鐵路客車車輛的軸箱彈簧斷裂情況，以彈簧斷裂后的故障狀態為研究工況，分別建立了斷裂接觸和斷裂失效兩種理論力學模型。

(2)通過對某鐵路客車車輛的6種軸箱彈簧故障工況進行動力學仿真分析，可知：6種軸箱彈簧故障工況下的輪軸橫向力和脫軌系數指標與正常工況時差別不大；內外簧全部斷裂失效工況下引起的輪重減載率指標比正常工況增大14%；軸箱彈簧故障狀態中，外簧斷裂失效工況下引起的構架橫向加速度比正常工況增大5%，而內外簧全部斷裂但仍接觸工況下引起的構架垂向加速度比正常工況增大12%；軸箱彈簧故障對車體平穩性的影響有限，且僅表現在垂向，橫向幾乎不變。

(3)研究表明，當轉向架有一處軸箱彈簧發生斷裂故障后，將一定程度地惡化車輛各動力學指標，但整體仍在安全范圍內。因此，若不考慮彈簧斷裂瞬態行為和構架結構扭轉剛度因素，僅從斷簧垂直坐落后的穩態角度而言，設計速度為160 km/h以內的鐵路客車車輛在僅發生一處軸箱彈簧斷裂故障后，適當降低速度繼續運行至臨近站點再進行換簧作業是可行的。

[1] Priyanka G, Shankapal S R. Failure investigation of a freight locomotive suspension spring and redesign of the spring for durability and ride index[J]. The Technical Journal of MSRSAS, 2012, 11(2): 23-29.

[2] Kumar K P, Kumar S P, Mahesh G G. Static analysis of a primary suspension spring used in locomotive[J]. International Journal of Mechanical Engineering and Robotics Research, 2013, 2(4): 430-436.

[3] 劉國云,曾 京.鋼彈簧故障狀態的車輛動力學性能[J].交通運輸工程學報, 2015, 15(4): 43-51.

[4] 劉 麗,張衛華,梅桂明,吳 娜.鋼彈簧故障狀態的車輛動力學性能[J].城市交通運輸研究, 2016(8): 20-24.

[5] 中國鐵路總公司.關于25T型客車軸箱彈簧折損分析及處置情況報告[R].北京：中國鐵路總公司, 2015.

[6] 嚴雋耄,傅茂海.車輛工程[M](第3版).北京:中國鐵道出版社,2008.

[7] European Committee for Standardization. EN 13906-1: 2002《Cylindrical helical springs made from round wire and bar-Calculation and design-Part 1: Compression springs》[S]. London: European Committee for Standardization, 2002.

[8] 王福天.車輛動力學[M].北京:中國鐵道出版社,1981.