新型PRRR+PURU+S球面并聯人形機器人踝關節機構靜剛度性能分析

周玉林 楊 龍,2 肖 超

1.燕山大學機械工程學院,秦皇島,066004 2.石家莊鐵道大學機械工程學院,石家莊,050043

0 引言

機構靜剛度對于機構的工程應用具有重要參考意義。目前，并聯機構靜剛度方面的研究已經取得一定進展。徐東濤等[1]以改進型Delta機構為研究對象,建立了彈性變形和重力參數的剛度模型。曲海波等[2]研究了一種4-RRS冗余球面并聯機構并對其進行了靜力學和剛度分析。CECCARELLI等[3]采用公式化剛度性能指標的方法，得到了Cassino并聯機構的剛度矩陣； TSAI等[4]將4種三自由度平動機構的剛度特性作了詳細的對比分析；CHAKAROV[5]建立了冗余并聯機構的剛度控制圖譜，并得到了該機構的剛度解析模型；王友漁等[6]以Tricept機械手的三自由度球坐標型并聯機構為例，提出了含恰約束支鏈的并聯構型裝備的靜剛度解析建模方法；汪滿新等[7]建立了一種基于全變形雅可比矩陣的混聯機器人模塊Bicept的靜剛度半解析模型；李樹軍等[8]基于守恒協調轉換剛度矩陣，推導出了3-RRR平面并聯機構剛度結構位形部分的解析表達式；趙鐵石等[9]基于影響系數法并借助虛功原理建立了空間并聯機構連續剛度非線性映射通用模型；胡波等[10]以傳統的3-RPS并聯機構為例，研究了考慮約束反力產生變形的剛度模型的建立方法；ZHOU等[11]利用彈性小變形疊加原理對UP+R二自由度球面并聯機構的靜剛度特性進行了詳細研究。

本文提出了一種新型PRRR+PURU+S球面并聯人形機器人踝關節機構，首先推導機構總變形與構件上各力的關系，再利用構件上各力與機構外載荷的關系(靜力學分析)，得到機構的靜剛度矩陣；將靜剛度矩陣正交化，從而得到機構的6個主剛度值及其所在的方向。實例計算的結果表明，新型踝關節機構的線位移剛度大幅增大，基本實現剛度均衡。

1 新型PRRR+PURU+S球面并聯人形機器人踝關節機構

圖1所示為UP+R踝關節機構。該機構的橫滾支鏈由連桿1和3個轉動副組成，俯仰支鏈由連桿2-1、連桿2-2(分別對應90°的圓心角)和3個轉動副組成；2個伺服電機M1、M2安裝在機架(固定叉架)上，電機軸互相垂直；動平臺的2個轉動副軸線垂直，可以實現2個方向的轉動。

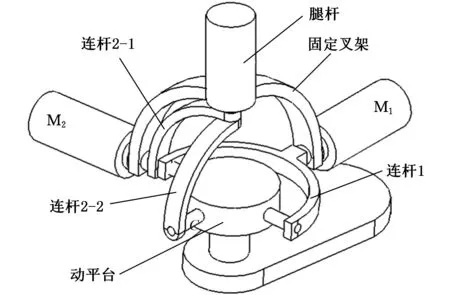
圖1 UP+R踝關節機構Fig.1 Ankle mechanism UP+R

UP+R踝關節機構保留了二自由度球面并聯機構UP+R的良好運動學特性，但是，由靜力學、靜剛度分析結果可知，UP+R踝關節機構2個運動支鏈的剛度非常小，不能滿足實際應用的要求。

為了增大UP+R踝關節機構的剛度，增加1條中心球面副約束支鏈，并對2個運動支鏈進行結構改進，從而得到新型PRRR+PURU+S踝關節機構，如圖2所示。

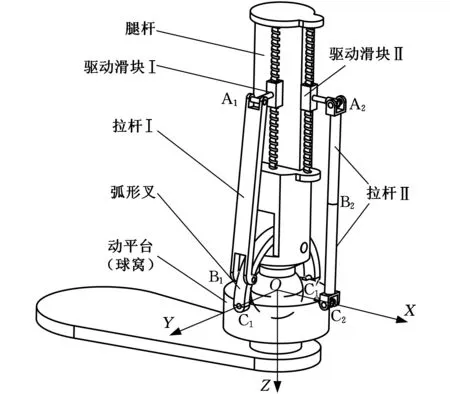
圖2 PRRR+PURU+S球面并聯人形機器人踝關節機構Fig.2 Spherical parallel humanoid ankle mechanism PRRR+PURU+S

支鏈2由機架、驅動滑塊Ⅱ、拉桿Ⅱ和動平臺組成。拉桿Ⅱ由通過轉動副B2連接的上、下拉桿組成，轉動副的軸線沿拉桿Ⅱ的長度方向。拉桿Ⅱ的上端、下端分別通過虎克鉸A2、虎克鉸C2與驅動滑塊Ⅱ、動平臺相連接。在初始位姿時，驅動滑塊Ⅱ的軸線和拉桿Ⅱ的軸線組成的平面垂直于弧形叉的平面。

支鏈3為機架和動平臺組成的中心球面副支鏈。在驅動滑塊Ⅰ和Ⅱ的驅動下，動平臺可以實現2個方向的擺動。

取中心球面副的球心點O為坐標原點,建立與機架固連的固定坐標系OXYZ。其中，Z軸與機架軸線重合，方向豎直向下，Y軸與支鏈1的轉動副軸線重合，方向如圖2所示，X軸方向軸由右手法則確定。

2 動平臺角位移及球心點線位移

為了便于研究，各轉動副處的變形和間隙忽略不計，并采取連續性假設、均勻性假設和各向同性假設，假設機構的所有構件(除動平臺)均滿足彈性小變形條件。

2.1 支鏈1傳遞到動平臺的變形

與弧形叉直接傳遞到動平臺的變形相比，驅動滑塊Ⅰ的變形和拉桿Ⅰ傳遞到動平臺的變形都非常小，故忽略不計，只考慮弧形叉的變形。

弧形叉的軸向變形和垂直桿件方向的變形相對于弧形叉扭轉和彎曲變形非常小，忽略不計。同時，轉動副B1處的作用力對弧形叉的扭轉和彎曲變形沒有影響，忽略不計。為便于研究弧形叉的變形，將其分為桿1-1和桿1-2兩部分，如圖3所示。

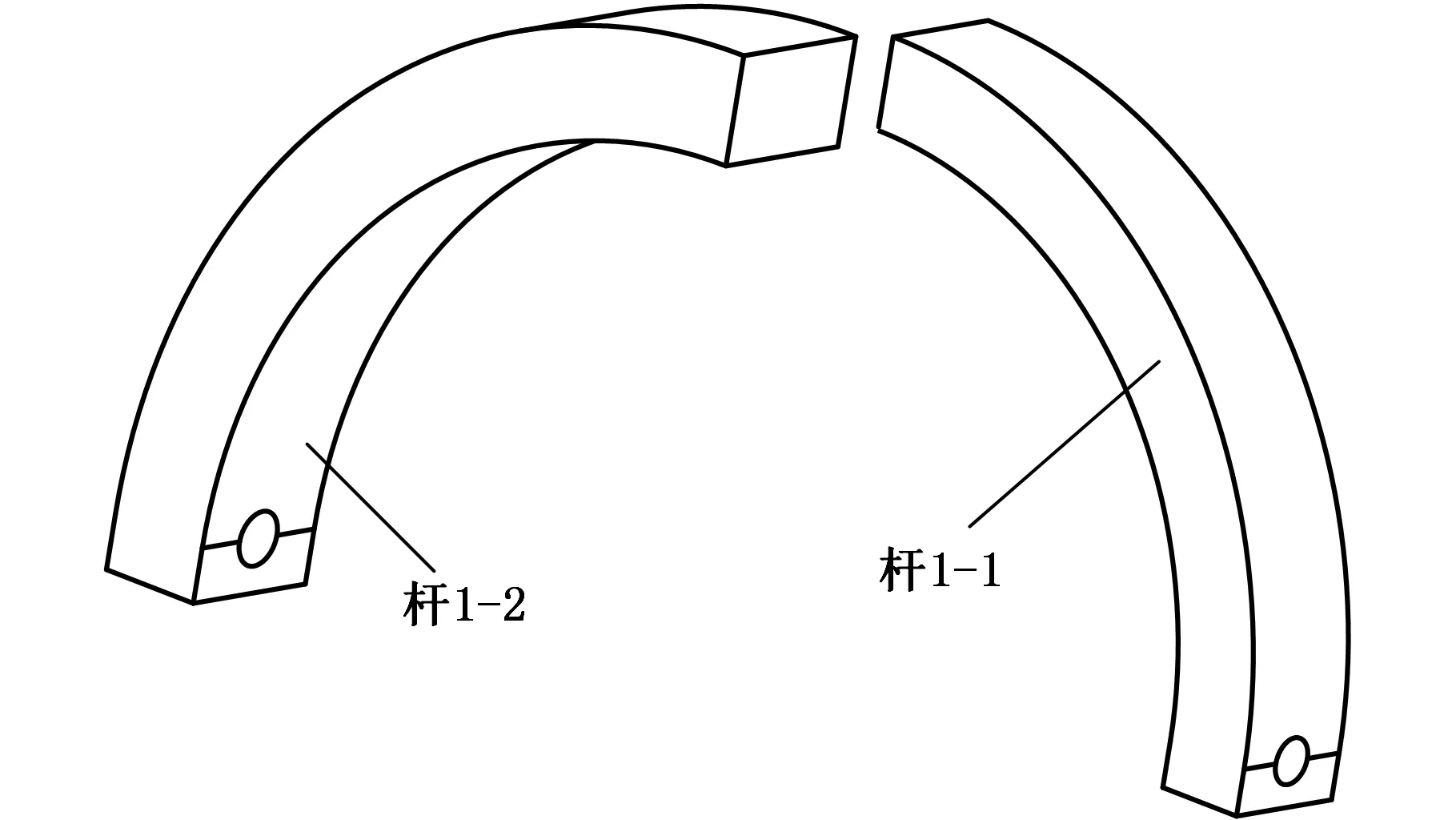
圖3 弧形叉示意圖Fig.3 Diagram of the arc-shaped fork

桿1-i(i=1,2)的一端受三個力F1i、R1i、P1i和兩個力矩Mf1i、Mr1i的作用，另一端簡化為固定端，如圖4所示。設弧形叉的切線方向為s方向，弧形叉的曲率半徑方向為m方向，垂直于弧形叉平面的方向為n方向。u1i、v1i、w1i(i=1,2)分別為固定坐標系下的單位方向矢量。Msi(φ)、Mmi(φ)、Mni(φ)為上述作用力引起的桿1-i任意截面φ處的力矩。當φ=90°時，Msi(φ)引起的扭轉變形為θsi；Mmi(φ)引起的撓度變形為νmi、轉角變形為θmi；Mni(φ)引起的撓度變形為νni、轉角變形為θni。所以，桿1-1和桿1-2與動平臺連接點的線位移、可傳遞到動平臺的角位移分別為

(1)

(2)

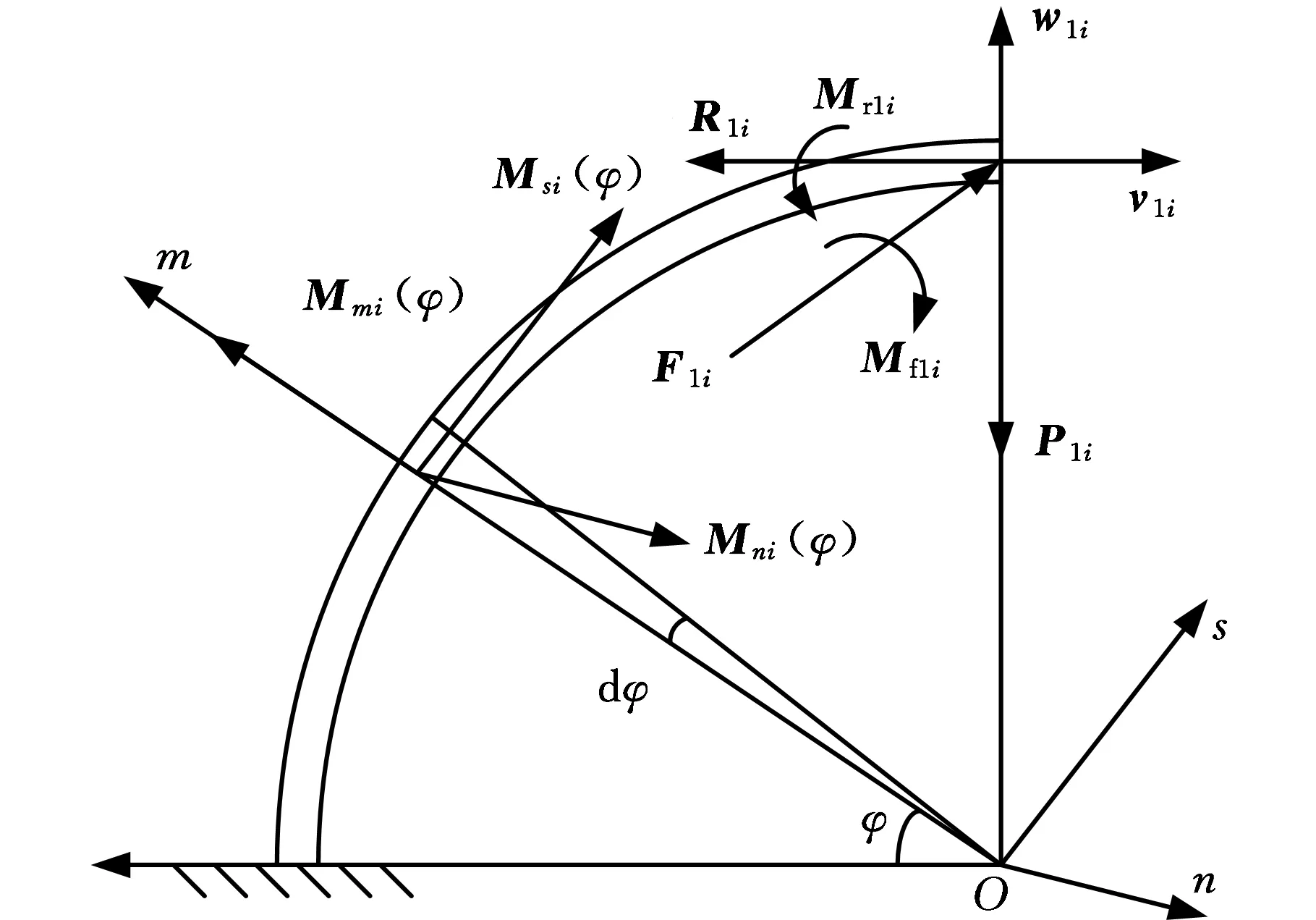
圖4 桿1-i簡化模型Fig.4 Simplified model of rod 1-i

2.2 支鏈2傳遞到動平臺的變形

在支鏈2的變形中，與拉桿Ⅱ的變形相比，驅動滑塊Ⅱ的變形非常小，忽略不計。設拉桿Ⅱ的上拉桿、下拉桿的拉伸變形分別為Δ21、Δ22。

動平臺會產生微小的位姿調整，假設上拉桿相對于驅動滑塊Ⅱ沿單位矢量u24、v24方向分別存在牽連角位移e21、e22，下拉桿相對于上拉桿沿單位矢量w23方向存在牽連角位移e23，則上拉桿、下拉桿的實際角位移分別為

(3)

由牽連角位移引起上、下拉桿產生的線位移分別為

(4)

式中，l2、l3分別為上拉桿、下拉桿的長度。

由小變形疊加原理，分別得到下拉桿與動平臺的連接點處的線位移、角位移的表達式如下：

(5)

2.3 支鏈3傳遞到動平臺的變形

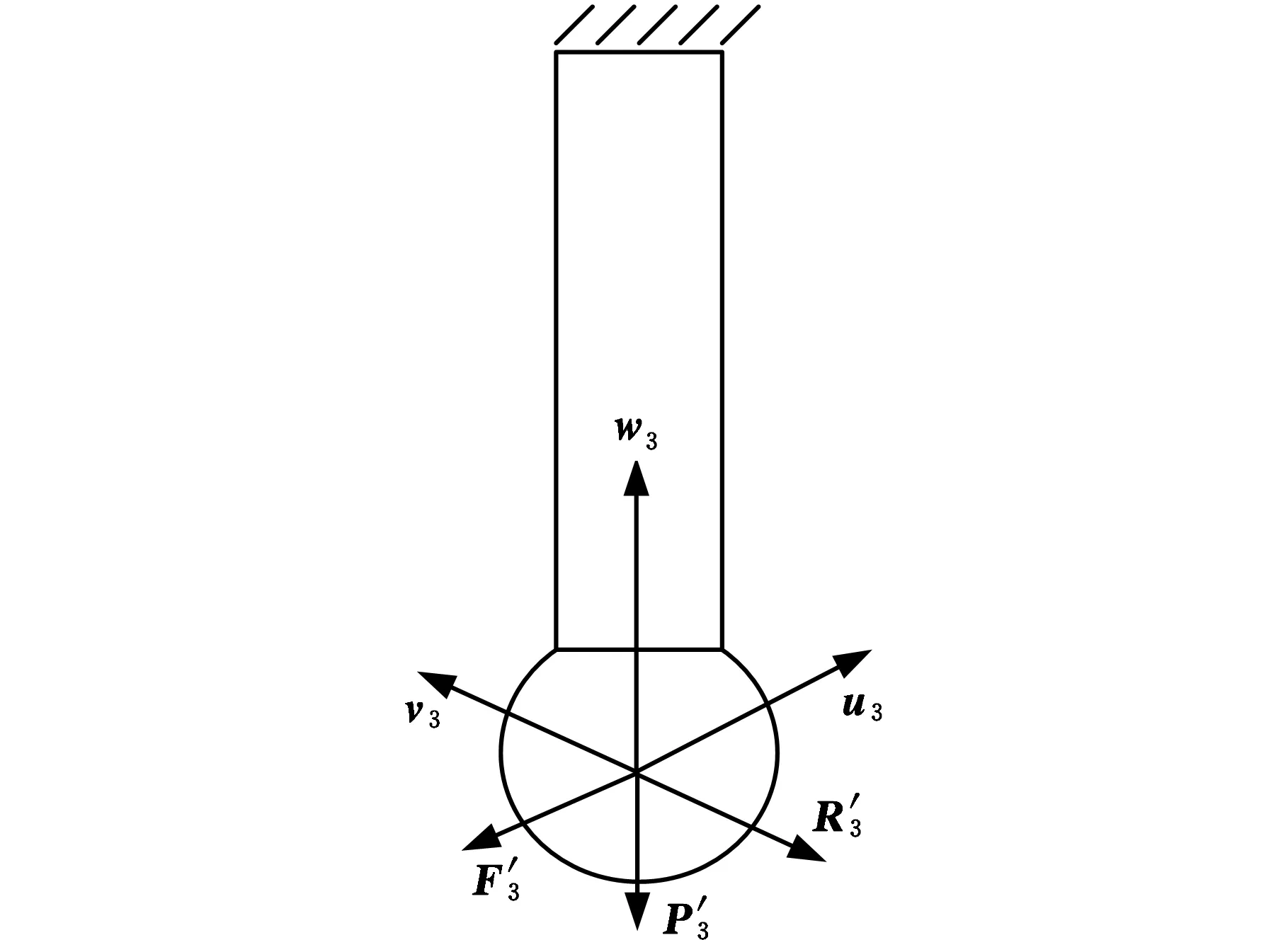
圖5 機架的簡化模型Fig.5 Simplified model of rack

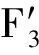
Δ3=νf3u3+νr3v3+νp3w3

(6)

式中,u3、v3、w3均為單位矢量。

2.4 動平臺角位移與球心點線位移

三條支鏈的小變形使動平臺產生微小的位姿調整，假設動平臺相對于機架沿單位矢量u3、v3、w3方向的角位移分別為e01、e02、e03，則動平臺的角位移、動平臺與弧形叉的兩個連接點的角位移分別為

(7)

三條支鏈與動平臺連接處的線位移與動平臺角位移的矢量關系如圖6所示。

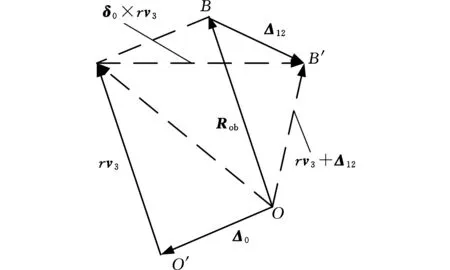
圖6 位移矢量關系Fig.6 Relationship between displacement vectors

所以，球心點的線位移有以下4種表達形式：

(8)

式中,r為動平臺半徑。

3 機構的剛度矩陣

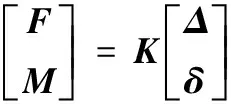
(9)

Δ=Δo2=G2C2Fg

(10)

(11)

(12)

(13)

(14)

(15)

式中，K為機構的靜剛度矩陣；E為連桿的彈性模量；C2為4×6系數矩陣，由靜力學分析得到，每一項元素均為機構位姿與參數的函數;G2為3×4系數矩陣；Iy為y軸截面慣矩；Iz為z軸截面慣矩；G為切變模量；β為截面系數；h為截面尺寸高；b為截面尺寸寬；q221、q23、υ2、o23、o221均為固定坐標系下的方向矢量。

同理可得

δ=δD2=G22C22Fg

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

其中，C22為12×6系數矩陣，由靜力學分析得到,每一項元素均為機構位姿與參數的函數；G22為3×12系數矩陣；各三角函數均為輸出位姿角的函數；af23、f13f13、…、c21m2p3均為機構位姿的函數。

故動平臺球心點的總位移與外載荷的關系為

(26)

機構的柔度矩陣為

(27)

當柔度矩陣非奇異時，將式(27)整理可得

(28)

與式(9)比較，得到機構的靜剛度矩陣如下：

K=Ξ-1

(29)

4 機構的主剛度及方向

利用正交變換的方法將機構的靜剛度矩陣對角化，得到機構的6個主剛度及它們所在的方向。

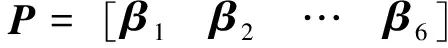
由上述分析得

(30)

令

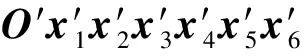
從而有

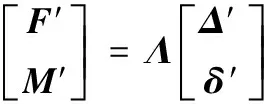
(31)

即，機構在新坐標系下的靜剛度矩陣變為

(32)

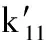
取新坐標系的坐標軸方向的單位矢量如下：

(33)

5 機構剛度數值計算與分析

各構件均采用45鋼(切變模量G=80 GPa、彈性模量E=200 GPa)。拉桿Ⅰ和弧形叉的斷面尺寸h=10 mm、b=10 mm、β=0.141，拉桿Ⅰ的長度l1=80 mm，弧形叉的半徑r1=50 mm。拉桿Ⅱ的半徑r2=3 mm，上、下拉桿的長度l2=50 mm、l3=50 mm。

選擇動平臺的3個位姿，計算得到機構的靜剛度矩陣，將剛度矩陣對角化，得到機構的主剛度及主方向，見表1。計算結果表明，機構線位移剛度和角位移剛度基本達到剛度均衡。主剛度的值與方向隨著動平臺的位姿變化而變化，當位姿遠離零點(φx=φy=0)位置時,機構的剛度明顯增大。

在3個相同的輸出位姿下，比較新型踝關節機構與UP+R踝關節機構的主剛度值，如表2所示。分析發現新型踝關節機構的角位移剛度、線位移剛度均有增大，其中線位移剛度大幅增大，基本實現剛度均衡。

6 仿真驗證

選擇新型踝關節機構的兩個輸出位姿，假定外載荷為600 N垂直于動平臺過球心點的作用力，將理論計算得到的靜剛度矩陣，分別轉化為兩個輸出位姿時，機構動平臺中心點的線位移變形。

將上述踝關節機構三維模型導入到ANSYS軟件中，如圖7、圖8所示。在與理論分析相同的條件下進行仿真，分別得到兩個輸出位姿時，對應的動平臺中心點的線位移變形。

表1 PRRR+PURU+S踝關節機構的主剛度及主方向

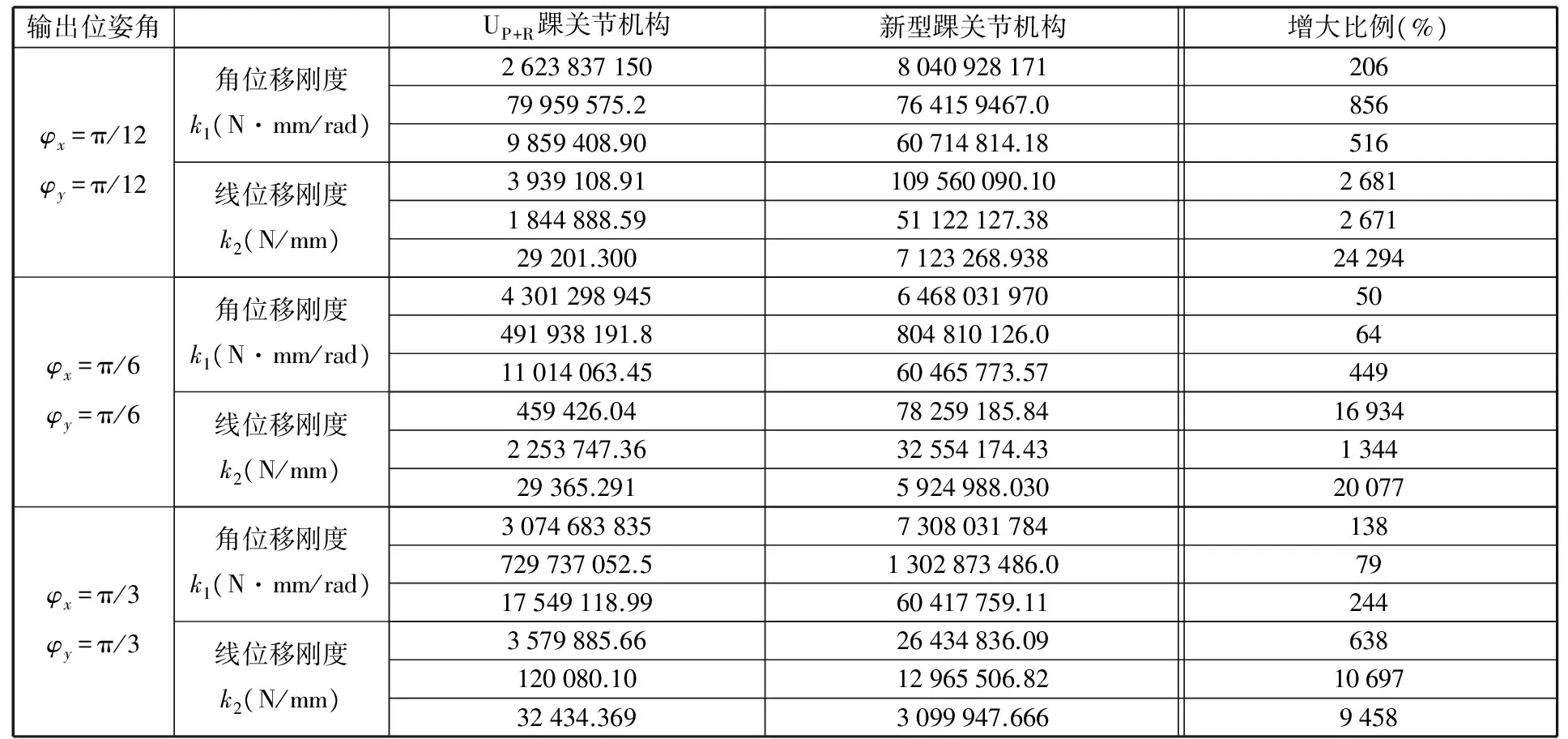
表2 兩個踝關節機構的主剛度值比較Tab.2 Comparison between principal stiffness of two ankle mechanisms

圖7 φx=π/12、φy=π/12時，變形仿真試驗Fig.7 Deformation simulation test when φx=π/12, φy=π/12

圖8 φx=π/6、φy=π/6時，變形仿真試驗Fig.8 Deformation simulation test when φx=π/6,φy=π/6

將仿真試驗結果與理論計算結果對比，如表3、表4所示。由表3和表4可知，兩者的相對趨勢是正確的、誤差在允許的范圍內。驗證了靜剛度理論分析結果的正確性。

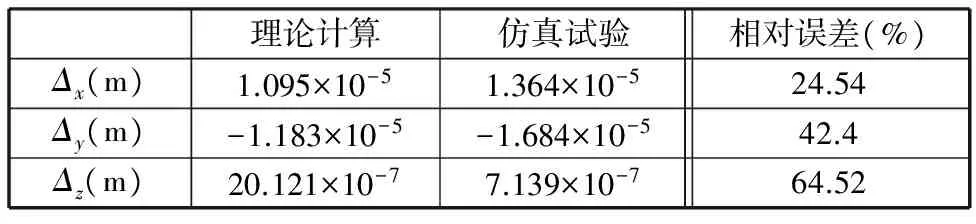
表3 φx=π/12、φy=π/12時，線位移比較Tab.3 Comparison between linear displacements whenφx=π/12,φy=π/12

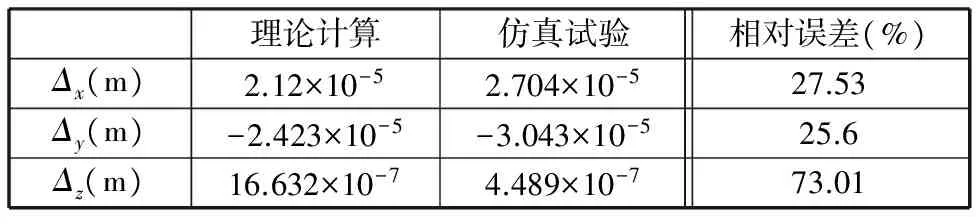
表4 φx=π/6、φy=π/6時，線位移比較Tab.4 Comparison between linear displacements whenφx=π/6,φy=π/6

7 結論

(1)提出了一種新型PRRR+PURU+S球面并聯人形機器人踝關節機構，導出了其靜剛度矩陣，對機構的靜剛度特性進行了詳細的研究。

(2)研究結果表明，新型PRRR+PURU+S踝關節機構的整體靜剛度除與機構參數、運動位姿有關外，還受過約束條件影響；與UP+R踝關節機構相比，角位移剛度、線位移剛度均有增大，其中線位移剛度大幅增大，基本實現了剛度均衡。

參考文獻：

[1] 徐東濤，孫志禮，于曉光. 考慮桿件彈性變形的改進型Delta并聯機構剛度特性分析[J]. 農業機械學報,2013,44(5)：294-298.

XU Dongtao, SUN Zhili, YU Xiaoguang. Stiffness Characteristic Analysis of Modified Delta Parallel Mechanism Based on Bars’ Elastic Deformation[J]. Transactions of the Chinese Society for Agricultural Machinery,2013,44(5):294-298.

[2] 曲海波，梁藝瀚，方躍法，等. 4-RRS冗余球面并聯機構的靜力學與剛度分析[J]. 機械工程學報，2015，51(11)：8-15.

QU Haibo, LIANG Yihan, FANG Yuefa, et al. Statics and Stiffness Analysis of 4-RRS Redundant Spherical Parallel Mechanism[J]. Journal of Mechanical Engineering,2015,51(11):8-15.

[3] CECCARELLI M, CARBONE G. A Stiffness Analysis for CaPaMan (Cassino Parallel Manipulator)[J]. Mechanism and Machine Theory,2002,37(5):427-439.

[4] TASI L W, JOSHI S. Comparison Study of Architecture of Four 3 degree-of-freedom translational parallel manipulators [C]//Proceedings of the 2011 IEEE International Conference on Robots and Automation. Seoul: IEEE，2001：1283-1288.

[5] CHAKAROV D. Study of the Antagonistic Stiffness of Parallel Manipulators with Actuation Redundancy[J]. Mechanism and Machine Theory,2004,39(6):583-601.

[6] 王友漁，黃田，CHETWYND D G，等. Tricept機械手靜剛度解析建模方法[J]. 機械工程學報，2008，44(8)：13-19.

WANG Youyu, HUANG Tian, CHETWYND D G, et al. Analytical Method for Stiffness Modeling of the Tricept Robot[J]. Chinese Journal of Mechanical Engineering,2008,44(8),13-19.

[7] 汪滿新，王攀峰，宋軼民，等.4自由度混聯機器人靜剛度分析[J].機械工程學報，2011，47(15)：9-16.

WANG Manxin, WANG Panfeng, SONG Yimin, et al. Stiffness Analysis of a 4-DOF Hybrid Robot[J]. Chinese Journal of Mechanical Engineering,2011,47(15):9-16.

[8] 李樹軍，GOSSELIN C.3-RRR平面并聯機構的剛度特性分析[J].東北大學學報(自然科學版)，2007，28(1)：91-94.

LI Shujun, GOSSELIN C. Stiffness Analysis and Stiffness Mapping of 3-RRR Planar Parallel Mechanism Based on CCT Stiffness Matrix[J]. Journal of Northeastern University (Natural Science),2007,28(1):91-94.

[9] 趙鐵石，趙延治，邊輝，等.空間并聯機構連續剛度非線性映射[J].機械工程學報，2008，44(8)：20-25.

ZHAO Tieshi, ZHAO Yanzhi, BIAN Hui, et al. Continuous Stiffness Nonlinear Mapping of Spatial Parallel Mechanism[J]. Journal of Mechanical Engineering,2008,44(8):20-25.

[10] 胡波，路懿.求解3-RPS并聯機構剛度的新方法[J].機械工程學報，2010，46(1)：24-29.

HU Bo, LU Yi. New Approach for Analyzing the Stiffness of 3-RPS Parallel Manipulator[J]. Journal of Mechanical Engineering,2010,46(1):24-29.

[11] ZHOU Yulin, YANG Long, LI Bo, et al. Stiffness Analysis of a Spherical Parallel Mechanism UP+Rwith 2-DOF[J]. Journal of Harbin Institute of Technology,2013,20(4)：41-47.