基于張量Tucker分解的發動機故障診斷

許小偉 沈 琪 嚴運兵 吳 強 張 楠

1.武漢科技大學汽車與交通工程學院，武漢， 430081 2.純電動汽車動力系統設計與測試湖北省重點實驗室，襄陽，441053

0 引言

在傳統的發動機故障診斷與預測中，監測的信號往往表現為時域或頻域上的一維信號，影響因素只有時間或頻率，而實際上發動機故障影響因素較多。復雜的高維數據在數據特征提取過程中，常利用波形分析法提取波動率變化最大值、波動率做功峰值、工倍頻發火能量比等參數，或者采用小波包重構與分解提取信號的能量特征值，并作為特征參數，以向量的模式作為模型的輸入[1]。這樣處理解決了高維數據的模型輸入問題，但會導致原始數據之間的自然結構信息丟失，多種模態特征之間的時序關聯共生性遭到破壞，產生的誤差也可能導致原始數據最有用的信息丟失，從而對后續的故障診斷造成影響[2]。

實際上發動機各個信號之間并不是相互獨立的，眾多信號相互干擾較大且帶有強烈的非線性和復雜耦合的特征。眾多信號源在數據分析中可以被表示成多維數組，即張量(tensor)。張量作為高維數據最自然的表示方式，不僅能夠最大程度保持數據的內在結構特性，而且在實際問題中表示事物時更能接近事物的本質屬性，這樣得到的模型也能更加準確[3]。張量Tucker分解是高階的主成分分析方法，能夠挖掘出張量的潛在結構，分解得到的核心張量以低維子空間的形式存儲原始張量，去除冗余信息后可以更為準確地表達原始張量。張量及張量分解理論目前被廣泛應用于數據壓縮、模式識別、圖像處理等領域[4-6]，而張量分解應用于發動機故障診斷還鮮見報道。

本文提出一種在張量空間構建發動機狀態樣本的方法，并基于張量Tucker分解和交替投影的思想，設計了一種高階奇異值分解[7](high order singular value decomposition，HOSVD)和高階正交迭代[8](high-order orthogonal iteration，HOOI)的聯立分解算法，對構建的張量型樣本進行低階近似處理，得到發動機監測信號的數據特征；然后利用分類器進行訓練和測試，對發動機單缸失火和軸系不對中進行故障診斷，證實了該張量構建方法和分解算法的有效性。

1 張量理論基礎

1.1 張量基本概念及記號

定義1 張量與張量空間。對于向量空間V(1)，V(2)，…，V(N)，定義外積(或稱張量積，記作?)空間V(1)?V(2)?…?V(N)為包含所有v(1)?v(2)?…?v(N)的線性組合的向量空間∑kv(1)?v(2)?…?v(N)，其中，v(1)，v(2)，…，v(N)分別為V(1)，V(2)，…，V(N)中的元素。其中外積?應滿足多線性,即

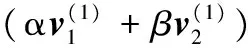
(1)

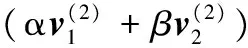
(2)

……

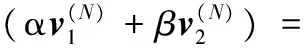
(3)

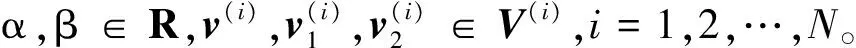
因此定義此空間中的元素X∈V(1)?V(2)?…?V(N)為N階張量。

定義2 張量的階。張量的階定義為形成所屬張量空間的向量空間的個數。從代數角度看，張量是向量在高維空間的拓展，零階張量為數量x，一階張量為向量X=(xi)，二階張量為矩陣X=[xij]，三階張量即是由若干個同維矩陣疊放在一起，形成的一個立方體式的數組X=[xijk]，更高階的張量則無法可視化描述。張量的每一階可以看作是一個影響因子，N階張量的每一個元素都可以看成是N個影響因子相互作用的結果。

定義3 張量的纖維。張量的纖維定義為只保留張量的一個下標可變，而固定其他所有下標得到的一路陣列。一個三階張量三個方向的纖維分別為模-1纖維(列纖維)X:jκ、模-2纖維(行纖維)Xi:κ、模-3纖維(管纖維)Xij:。

定義4 張量的切片。張量的切片定義為保留張量的兩個下標可變而固定一個下標得到的一系列矩陣。一個三階張量三個方向的切片分別為水平切片Xi::、側身切片X:j:和正面切片X::k，正面切片又簡記為Xk[3，9]。

1.2 張量運算

定義5 張量的范數。張量范數的定義與矩陣范數的定義相似，定義為把張量空間映射到實數域的一個函數，一個N階張量X∈RI1×I2×…×IN的范數為

(4)

定義6 張量的矩陣化。張量的矩陣化是將張量中的元素重新排列，得到一個矩陣的過程。對于一個N階張量X∈RI1×I2×…×IN，它的模-n矩陣化即重新組織張量的模-n纖維成為一個矩陣中的行或列，表示為X(n)，張量中的元素xij…k被映射成為矩陣中的元素xij。

定義7 張量的Tucker分解。N階張量X∈RI1×I2×…×IN可以近似表示成一個核心張量G∈Rg1×g2×…×gN沿每一階乘上一個矩陣：

X≈G×1A×2A×…×NA=

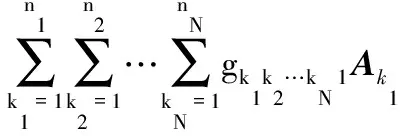
(5)

其中，1Ak1∈RI1×n1，2Ak2∈RI2×n2，…，NAkN∈RIN×nN被稱為因子矩陣，它們通常是正交的。在向量空間內，通常使用矩陣分解的方法來將復雜問題轉換成更易處理的問題，例如矩陣的滿秩分解、正交三角分解、奇異值分解等。在張量空間，同樣可以利用張量Tucker分解的方法，將高維問題轉換成低維問題[10-11]。

2 張量構建與分解算法

2.1 張量型發動機狀態樣本構建方法

在張量空間里構建發動機的狀態樣本，其中的每一階可以看作是一個對發動機的狀態進行影響的因子，張量里的每一個元素可以看作是各個影響因子相互作用的結果。

本文構建的發動機狀態樣本為三階張量X∈RI×J×K，第一階表示的影響因子為信號類別，例如各個部件受到的轉矩大小、進氣流量、進氣壓力、排氣溫度、冷卻水溫、噴油提前角等；第二階表示的影響因子為曲軸轉角，即樣本信號隨曲軸轉角的變化；第三階表示的影響因子為轉速，即在不同的轉速下樣本信號的變化。即完成了一個“信號類別×曲軸轉角×轉速”的三階張量型的發動機狀態樣本的構建，結構如圖1所示。所構建的三階張量型發動機狀態樣本中的每一個元素xijk(其中，i∈I,j∈J,k∈K)代表了在第k個轉速下、第i度曲軸轉角下的第j種信號參數值。

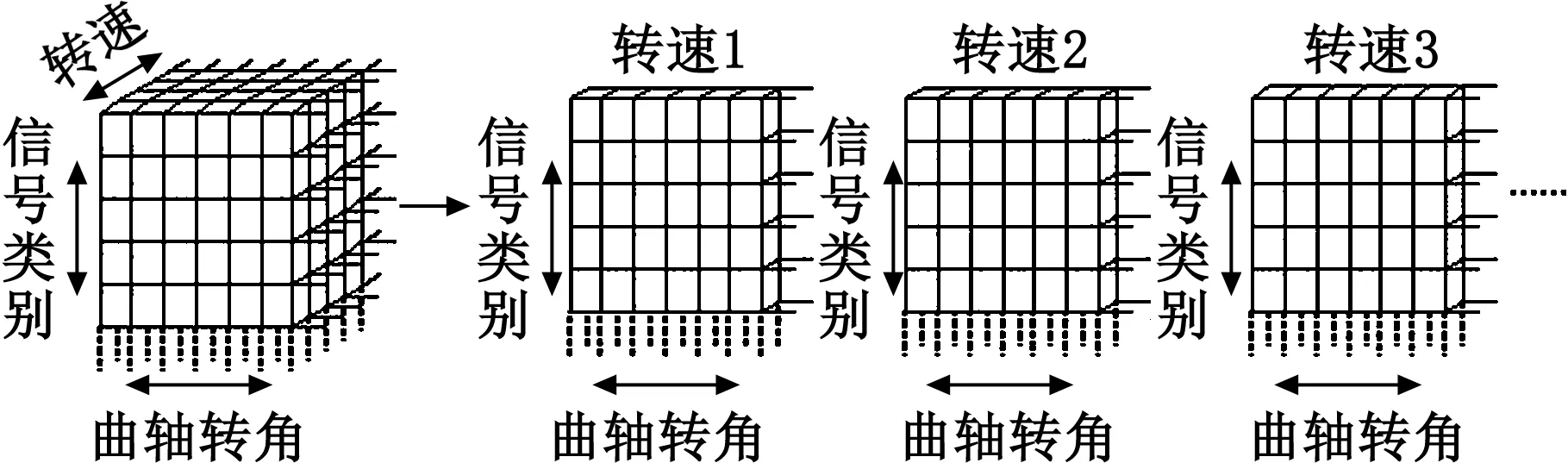
圖1 三階張量型發動機狀態樣本結構圖Fig.1 Structure of the engine state sample of thethree order tensor

2.2 張量Tucker分解算法

基于張量模式的分解算法能夠實現對高維張量數據的有效逼近，高階張量的Tucker分解可以看作是矩陣的奇異值分解以及主成分分析在高階上的推廣。在張量Tucker分解中，其本質是用一個核張量和若干正交的投影矩陣的積去近似原始張量，核心張量保留了原張量最主要的信息，在每一階上都比原張量小。以構建的三階張量X∈RI×J×K為例，張量Tucker分解可通過求解‖X-G×U1×U2×U2‖的最小值得到最優解[12]。由張量Tucker分解公式和張量范數性質，可將該最小值問題等價為最大值問題：

(6)

將Tucker分解寫成矩陣的形式，即

(7)

其中，因子矩陣U1、U2、U3分別為X(1)、X(2)、X(3)的前L、M、N個左奇異向量構成的矩陣。

如果分別對每個發動機狀態樣本進行張量Tucker分解，則各個樣本分解后所得到的投影因子均不相同，即投影之后的核心張量屬于不同的表征空間，這樣導致后續的分類過程無法進行。因此，為了使投影后的核心張量屬于同一表征空間，需要尋找一組相同的投影因子。HOSVD算法和HOOI算法是兩種常用的張量Tucker分解算法，HOSVD的基本思想是利用矩陣分析中的奇異值分解算法對張量中的每一個切片進行一次分解，采用低階近似處理，過濾掉某些較小的奇異值；HOOI的基本思想是使用交替投影的方法多次迭代求得最優結果。HOSVD的結果不能保證得到一個較好的近似值，但可以作為HOOI的一個很好的初始解[13]，故可使用HOSVD張量Tucker分解算法對每個樣本進行一次求解計算，其結果作為HOOI張量Tucker分解算法的輸入，再使用HOOI算法完成分解。圖2展示了張量分解算法流程。

2.3 發動機故障診斷流程

由于信號類別量綱的不同，需要先對每一個類別的信號數據進行歸一化處理，然后構建張量型樣本，接下來使用HOSVD-HOOI張量Tucker分解算法得到核心張量，核心張量在每一階上的尺寸均小于原始張量的尺寸，最后對每個核心張量進行向量化，得到分類器的輸入。隨機選取部分樣本作為訓練集，分別采用網格參數優化法[14]、遺傳算法[15]、粒子群算法[16]對分類模型中的參數進行優化。訓練完畢后，將剩余樣本作為測試集，對故障進行預測。基于張量Tucker分解的發動機數據特征提取及診斷流程如圖3所示。

3 實驗與分析

3.1 訓練與測試樣本

圖4所示為康明斯4B3.9-G2型發動機在轉速為1500 r/min時正常工作、單缸失火故障、軸系不對中故障三種狀態下的實驗樣本數據，分別描述了曲軸端轉矩、飛輪慣性力矩、曲柄銷處的連桿力、連桿軸向力四種參數隨曲軸轉角的變化關系，故構建的三階發動機狀態樣本第一階大小為4維。實驗中，將曲軸轉角設置為一個周期內的 0°～720°，作為仿真時長，采樣間隔為1°，故構建的三階發動機狀態樣本第二階大小為720維；轉速設置為1500～3000 r/min，采樣間隔為50 r/min，故第三階大小為31維。即構建的張量樣本X∈R4×720×31，每一個張量樣本中有4×720×31個數據。總共仿真48×31次，得到48個樣本。

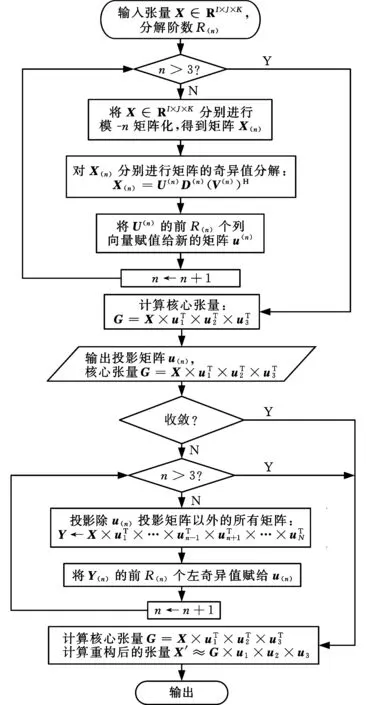
圖2 HOSVD-HOOI張量Tucker分解算法流程Fig.2 Algorithm flow of the HOSVD-HOOI tensor Tucker decomposition

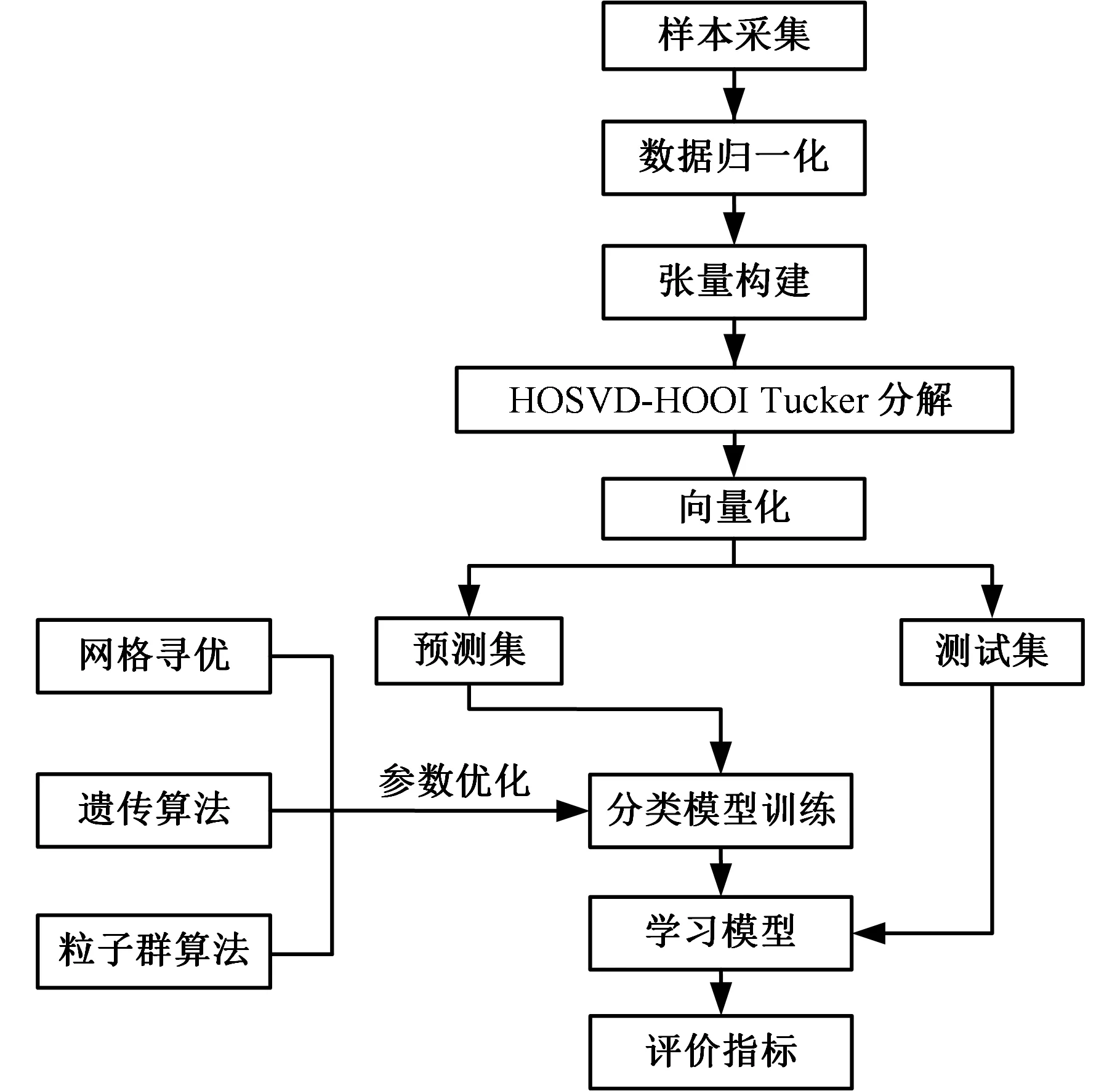
圖3 診斷流程圖Fig.3 Flow chart of diagnosis

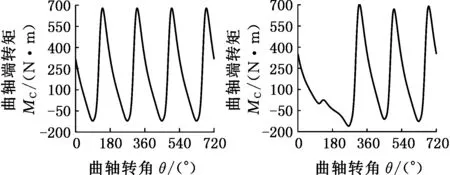
(a)正常工作時曲軸端轉矩(b) 單缸失火時曲軸端轉矩

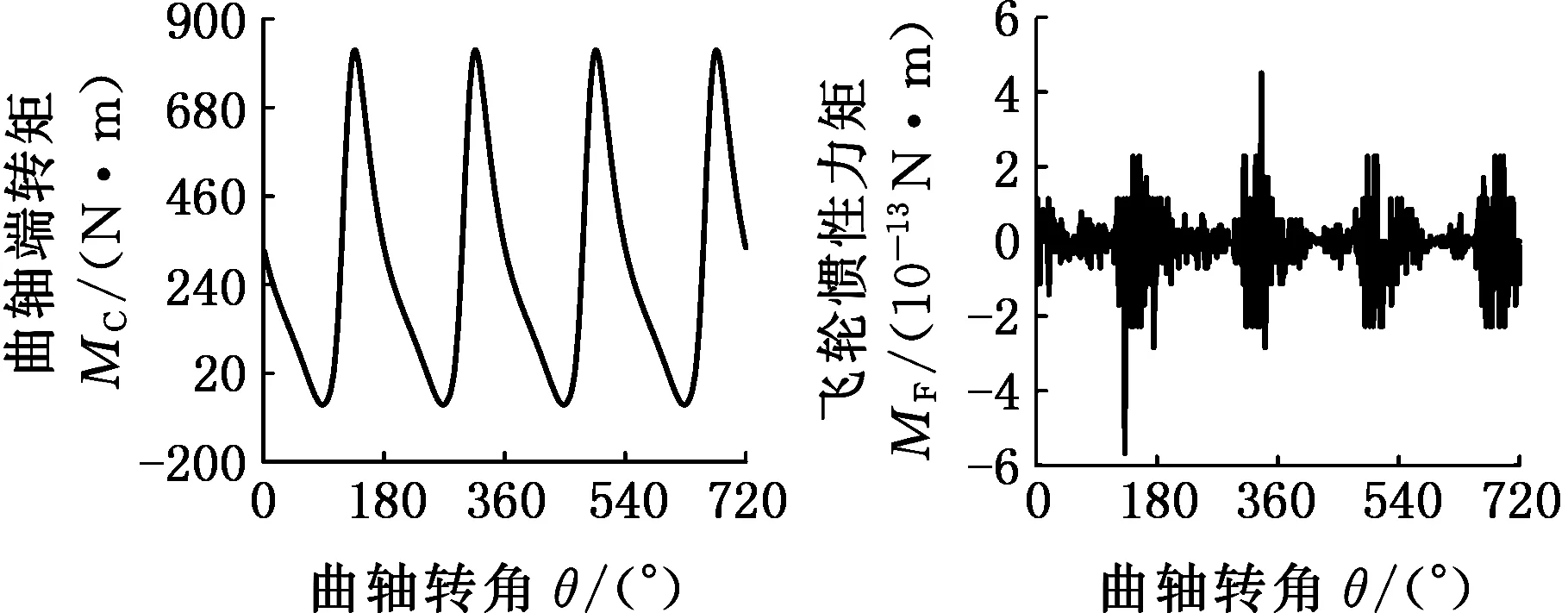
(c)軸系不對中時曲軸端轉矩(d)正常工作時飛輪慣性力矩

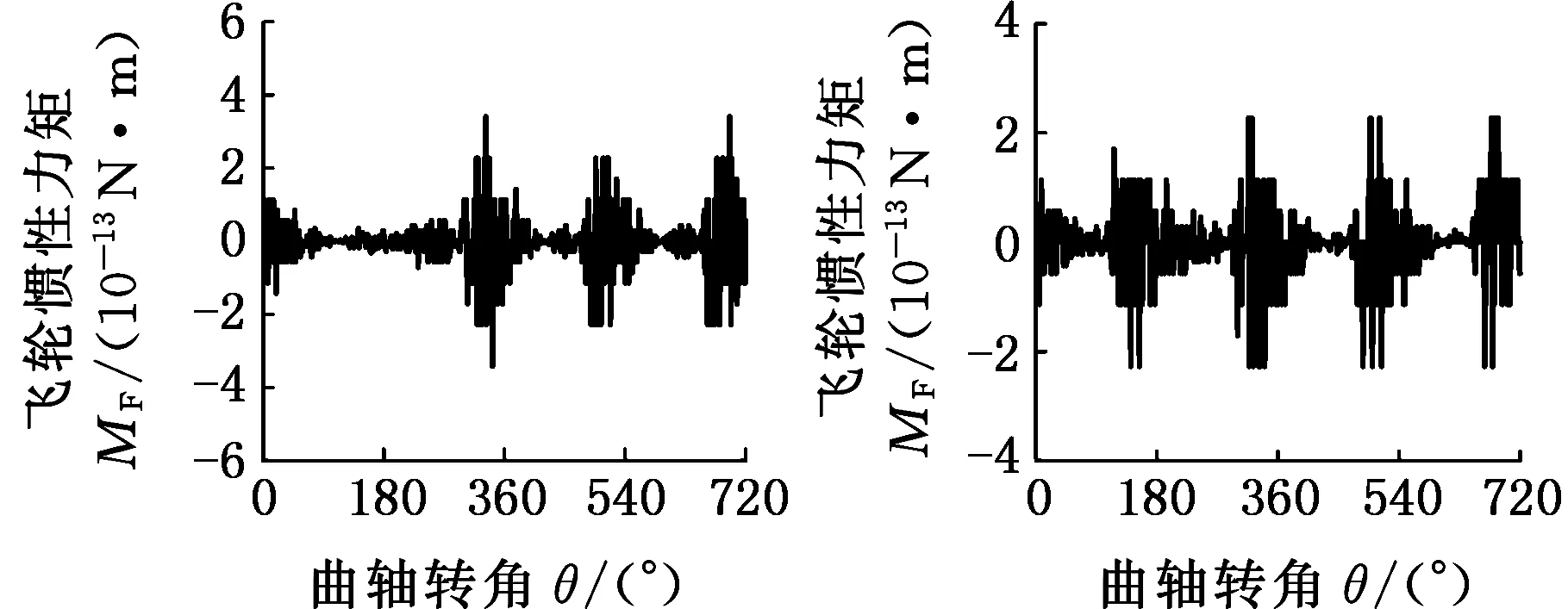
(e)單缸失火時飛輪慣性力矩(f)軸系不對中時飛輪慣性力矩

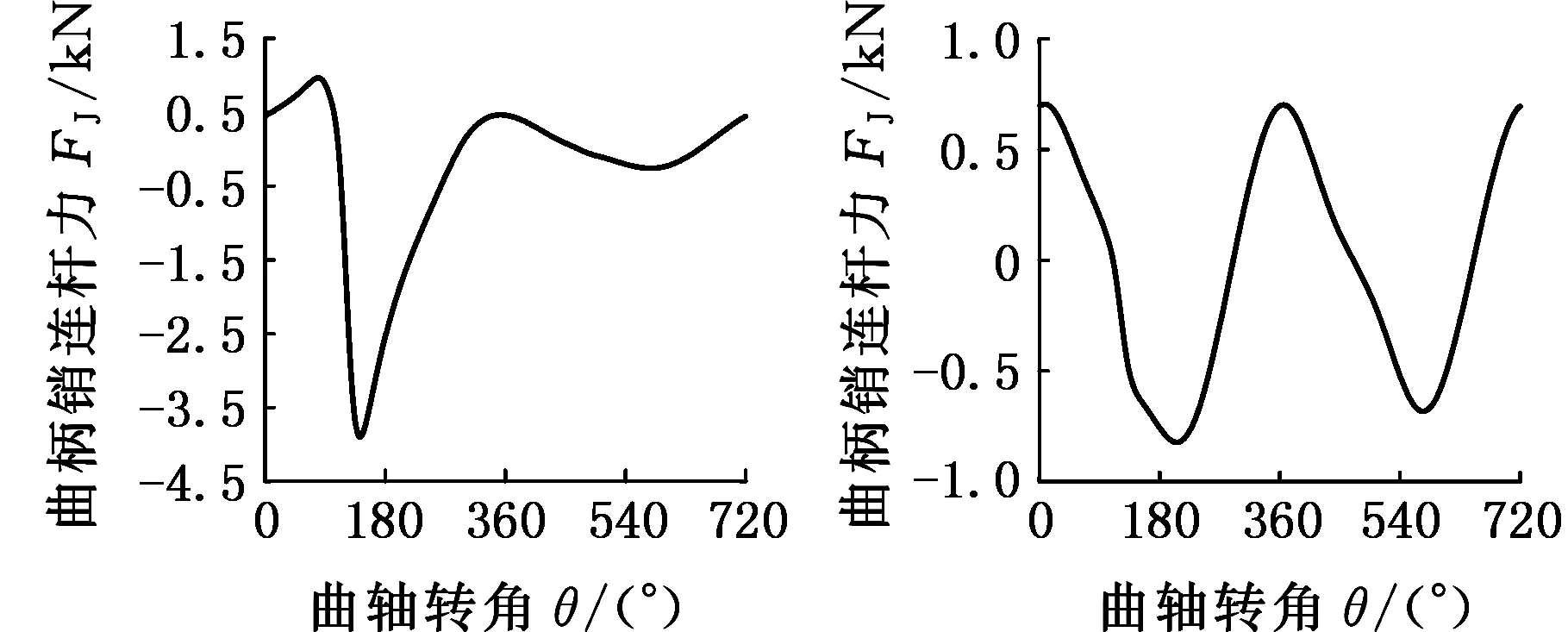
(g)正常工作時曲柄銷連桿力(h)單缸失火時曲柄銷連桿力

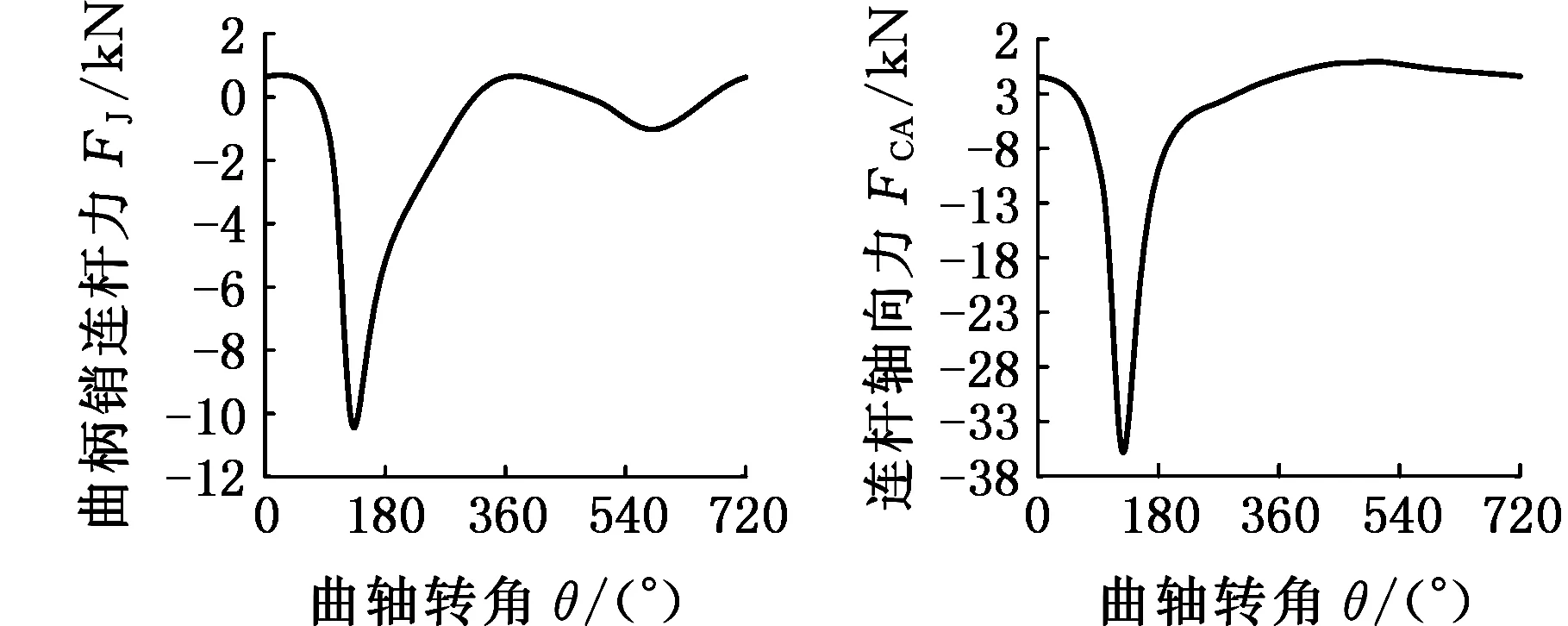
(i)軸系不對中時曲柄銷連桿力(j)正常工作時連桿軸向力

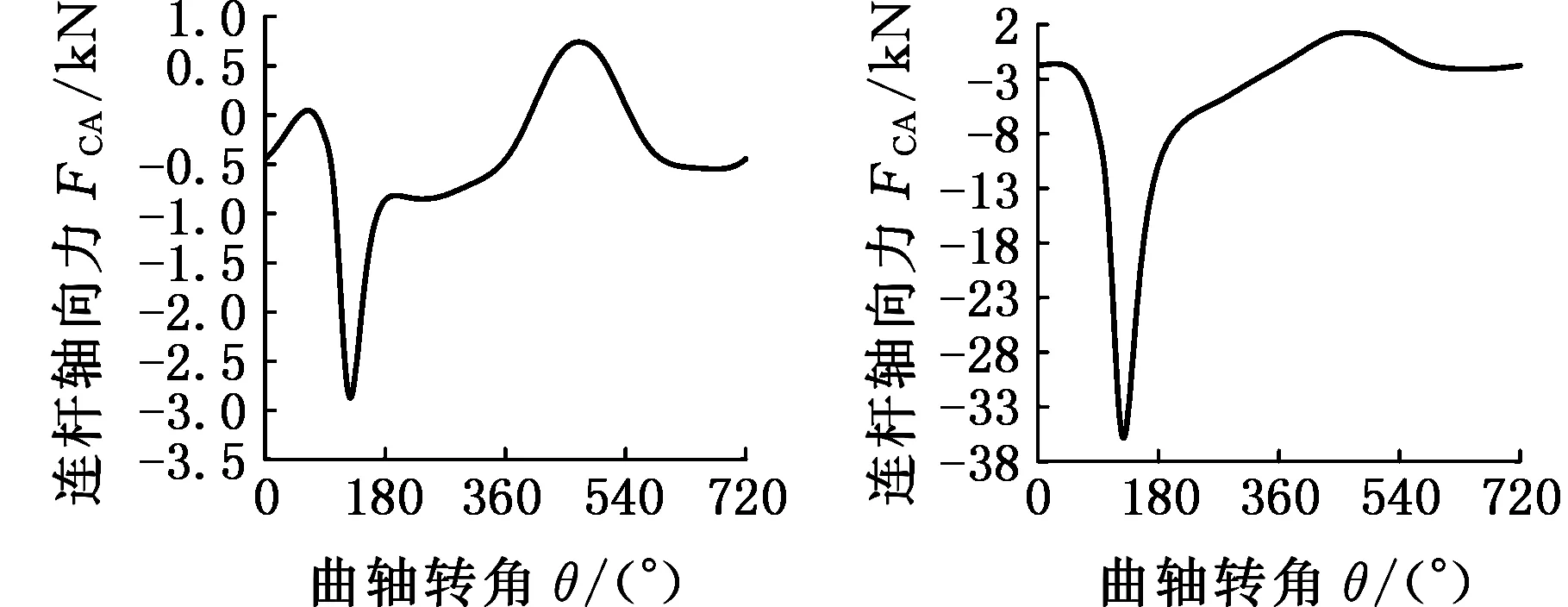
(k)單缸失火時連桿軸向力(l)軸系不對中時連桿軸向力圖4 實驗樣本數據Fig.4 Experimental sample data

將4×31×48個長度為720的向量形式的實驗數據加載至MATLAB中，接下來取某一個轉速下得到的四個信號數據，將曲軸端轉矩、飛輪慣性力矩、曲柄銷處的連桿力和連桿軸向力依次存儲為第一至第四行，得到一個大小為4×720的矩陣。按照此方法，將每一個轉速下得到的信號數據存儲為矩陣，最終得到31個大小為4×720的矩陣。由定義4可知該矩陣即為張量的正面切片X::k。將正面切片矩陣歸一化處理后，接下來創建大小為4×720×31的單位張量，并將31個大小為4×720的矩陣依次賦值給該單位張量的正面切片，從而完成一個三階張量型發動機狀態樣本的構建。按照此方法完成48個張量型發動機狀態樣本的構建，隨機選取24個樣本作為訓練集，剩余24個樣本作為測試集，用于后續的算法驗證。

3.2 實驗結果分析

為驗證張量型發動機狀態樣本構建方法和HOSVD-HOOI張量Tucker分解算法的有效性，實驗首先使用張量Tucker分解算法進行數據特征提取，并分別采用網格參數優化法、遺傳算法、粒子群算法對分類模型中的參數進行尋優，得到三種優化算法下的預測準確率和分類模型學習時間；接下來不使用Tucker分解算法，直接將向量型樣本數據輸入分類器，同時也采用上述三種參數尋優法對分類模型中的參數進行尋優，得到三種優化算法下的預測準確率和分類模型學習時間。

將發動機正常工作、單缸失火、軸系不對中三種狀態分別用類別標簽0、1、2表示，圖5給出了采用張量Tucker分解進行特征提取，并使用遺傳算法對分類模型中的參數進行尋優時得到的分類結果：正常工作狀態8個樣本全部正確分類；單缸失火故障有7個樣本被正確分類，1個樣本被誤分為軸系不對中故障；軸系不對中故障有7個樣本被正確分類，1個樣本被誤分為單缸失火故障。24個測試樣本正確分類22個，預測準確率為91.67%。圖6給出了未進行張量Tucker分解提取特征，使用遺傳算法對分類模型中的參數進行尋優時得到分類結果：正常工作狀態8個樣本全部正確分類；單缸失火故障有7個樣本被正確分類，1個樣本被誤分為軸系不對中故障；軸系不對中故障有6個樣本被正確分類，2個樣本被誤分為單缸失火故障。24個測試樣本正確分類21個，預測準確率為87.50%。

圖5 張量Tucker分解后的分類結果Fig.5 Classification results after tensor Tucker decomposition

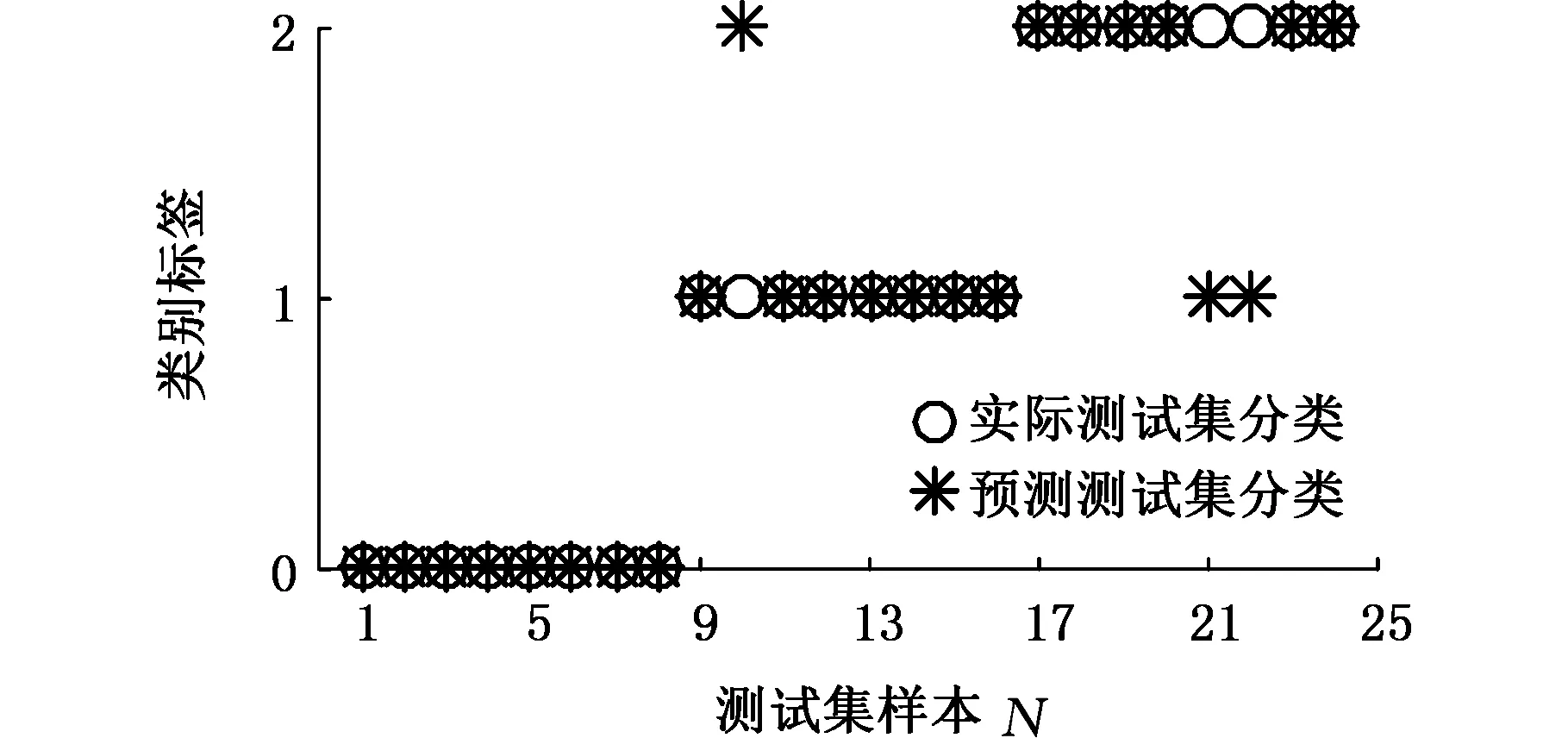
圖6 未進行張量Tucker分解后的分類結果Fig.6 Classification resultswithout tensor Tucker decomposition

將6次實驗結果繪制成表1，由表1可以看出，所有實驗結果的預測準確率均達到了80%以上，滿足工程應用的需求。對比三種參數優化算法，使用張量Tucker分解算法進行數據特征提取后，網格尋優法得到的分類準確率最高，粒子群算法次之，遺傳算法最低；未進行特征提取、直接將向量型樣本數據輸入分類器后，網格尋優法得到的分類準確率最高，遺傳算法次之，粒子群算法最低。無論是否進行特征提取，使用遺傳算法的模型學習時間最短，粒子群算法次之，網格尋優法最長。且基于張量Tucker分解的數據特征提取方法的預測準確率均高于未進行特征提取得到的預測準確率，且前者學習時間均短于后者，實用性更強。

表1 實驗結果

4 結論

(1)通過采集發動機曲軸端轉矩，飛輪慣性力矩等信號參數，構建了“信號類別×曲軸轉角×轉速”的三階張量形式的發動機狀態樣本，歸一化處理后，基于交替投影的思想，使用HOSVD張量Tucker分解和HOOI張量Tucker分解的聯立求解算法，將高維張量映射成尺寸更小的核心張量。

(2)分別采用網格參數優化法、遺傳算法、粒子群算法對分類模型中的參數進行尋優，以預測準確率和學習時間作為評價指標。實驗結果表明使用網格尋優法得到的預測準確率最高，使用遺傳算法的模型學習時間最短。

(3)將使用張量Tucker分解后得到核心張量向量化后輸入分類器進行訓練，并與未進行特征提取、直接將向量型樣本數據輸入分類器訓練作比較。實驗結果證明基于張量Tucker分解的發動機數據特征提取方法進行故障診斷有著較高的預測準確率和較短的分類模型學習時間，具有較強的實用性。

參考文獻：

[1] 張宇飛, 么子云, 唐松林,等. 一種基于主成分分析和支持向量機的發動機故障診斷方法[J]. 中國機械工程, 2016, 27(24): 3307-3311.

ZHANG Yufei,YAO Ziyun,TANG Songlin, et al. An Engine Fault Diagnosis Method Based on PCL and SVM[J]. China Mechanical Engineering, 2016,27(24): 3307-3311.

[2] HOU C, NIE F, ZHANG C, et al. Multiple Rank Multi-linear SVM for Matrix Data Classification[J]. Pattern Recognition, 2013, 47(1): 454-469.

[3] 楊兵. 基于張量數據的機器學習方法研究與應用[D]. 北京：中國農業大學, 2014.

YANG Bing. Research and Application of Machine Learning Algorithm Based Tensor Representation [D]. Beijing:China Agricultural University, 2014.

[4] KARAMI A, YAZDI M, MERCIER G. Compression of Hyperspectral Images Using Discerete Wavelet Transform and Tucker Decomposition[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2012, 5(2): 444-450.

[5] BENETOS E, KOTROPOULOS C. Non-negative Tensor Factorization Applied to Music Genre Classification[J]. IEEE Transactions on Audio Speech & Language Processing, 2010, 18(8): 1955-1967.

[6] ZHANG Q, WANG Y, LEVINE M D, et al. Multisensor Video Fusion Based on Higher Order Singular Value Decomposition[J]. Information Fusion, 2015, 24(C): 54-71.

[7] BARANYI P. Numerical Reconstruction of the HOSVD Based Canonical Form of Polytopic Dynamic Models[C]// International Symposium on Computational Intelligence & Intelligent Informatics. New York, 2007: 111-116.

[8] SHEEHAN B N, SAAD Y. Higher Order Orthogonal Iteration of Tensors (HOOI) and Its Relation to PCA and GLRAM[C]//SIAM International Conference on Data Mining. Minneapolis, Minnesota, USA, 2007:196-199.

[9] HACKBUSCH W. Tensor Spaces and Numerical Tensor Calculus[M].Heidelberg:Springer, 2012.

[10] KOLDA T G, BADER B W. Tensor Decompositions and Applications[J]. SIAM Review, 2009, 51(3): 455-500.

[11] CARROLL J D, CHANG J J. Analysis of Individual Differences in Multidimensional Scaling via ann-way Generalization of “Eckart-Young” Decomposition[J]. Psychometrika, 1970, 35(3): 283-319.

[12] 劉亞楠.基于圖和低秩表示的張量分解方法及應用研究[D]. 合肥：安徽大學, 2014.

LIU Yanan. Tensor Decomposition and Its Applications Based on Graph and Low Rank Representation[D]. Hefei:Anhui University,2014.

[13] SUN J, TAO D, PAPADIMITRIOU S, et al. Incremental Tensor Analysis: Theory and Applications[J]. ACM Transactions on Knowledge Discovery from Data, 2008, 2(3): 651-678.

[14] 王健峰. 基于改進網格搜索法SVM參數優化的說話人識別研究[D]. 哈爾濱：哈爾濱工程大學, 2012.

WANG Jianfeng. Speaker Recognition Based on Improvedgrid Search Algorithm for SVM Parameter Optimization[D]. Harbin: Harbin Engineering University, 2012.

[15] 汪松泉. 遺傳算法在組合優化中的應用研究[D]. 合肥：安徽大學, 2010.

WANG Songquan. Application of Genetic Algorithm in Combinatorial Optimization[D]. Hefei:Anhui University,2010.

[16] 張麗平. 粒子群優化算法的理論及實踐[D]. 杭州：浙江大學, 2005.

ZHANG Liping. Theory and Practice of Particle Swarmoptimization Algorithm[D]. Hangzhou:Zhejiang University, 2005.