基于列車縱向縮比模型的摩擦力尺寸效應研究

張 凱， 許 平， 姚曙光(中南大學 交通運輸工程學院, 湖南 長沙 410075)

由于列車碰撞事故具有很強的隨機性，因此在積極主動地采取各種措施盡可能避免列車事故的同時，研究列車被動安全防護技術也顯得尤為重要。目前關于列車耐撞性的研究主要是以數值模擬的形式進行[1-6]。然而與汽車、船舶等交通工具單體撞擊不同，列車由多節車輛編組而成，撞擊過程中既有單節車的受撞破壞問題，又有各車輛間的耦合互撞等問題。列車系統的強非線性、邊界條件的復雜性，對數值模擬方法的可靠性和準確性提出了極大地挑戰。實車碰撞試驗是開展列車耐撞性研究最為可靠的方法，但是其代價過于昂貴，耗時較長且難以操作。列車縮比等效碰撞模型為列車的耐撞性研究提供了一種新的研究途徑和方法，這對于多方面、多角度的開展優化動車組的耐撞擊設計，提高列車運營安全性具有重要的現實意義。縮比模型試驗具有操作簡單、可重復性高及結果穩定等優點，廣泛應用于飛機、輪船、汽車以及橋梁結構等領域的耐撞性研究。2008年Tabri[7-9]對2個實船縮比模型進行低速碰撞試驗研究，基于13個試驗工況，研究了2個輪船質量比、碰撞速度、結構響應對于形變吸能的影響；Lowe和Al-Hassani[10]在1972年對10種1∶25的雙層客車縮比模型碰撞行為開展了研究，進行準靜態壓縮和落錘動態沖擊試驗，并指出不同比例模型試驗結果與全尺寸模型的相關性；Xu[11]等根據Buckinham π定理，采用落錘形式，開展了20 t中型油罐車與3種典型鋼橋梁上部結構發展碰撞的縮比模型試驗，研究不同橋梁的上部結構變形失效特征；Zhu等通過采用高速列車的縮比模型開展風洞試驗，研究高速列車的空氣動力學性能[12]。在縮比等效模型中，由于尺寸效應的存在，使得一些參數很難按比例進行縮放，這些沒有被注意到的重要變量，往往被人為的認為是非關鍵因素而不予以考慮，但是這些參數的影響是不容忽略的。本文進行列車1/8比例碰撞縮比試驗，針對列車縱向縮比等效模型中輪軌摩擦力載荷(以下簡稱摩擦力載荷)難以精確縮比的情況，開展大量動力學仿真計算，研究輪軌摩擦系數(以下簡稱摩擦系數)對列車碰撞過程中能量耗散規律的影響，并對摩擦力載荷提出相應的修正措施，實現不同摩擦系數間的相互轉化。

1 列車縱向縮比模型及摩擦力尺寸效應

集中質量動力學模型具有模型簡單、計算速度快等優點，廣泛用于車輛碰撞領域[13-14]。根據列車縱向動力學理論，將組成列車的各節車輛簡化為單一質點，將連接相鄰車輛的車鉤緩沖裝置考慮為非線性彈簧，非線性彈簧同時考慮了緩沖器的加載、卸載特性及壓潰管等吸能裝置的特性曲線。列車縱向碰撞模型僅考慮車體的縱向運動和變形，不考慮列車制動力，每個車體質點所受到的力包括與軌面之間的摩擦力以及相鄰車體之間的非線性彈簧力，利用牛頓第二運動定律，每個車體質點的運動方程為

( 1 )

根據相似性理論，為保證列車原型和縮比模型是相似的，式( 1 )中的物理變量應根據Buckinham定理進行縮放[15]。部分參數的比例因子見表1。

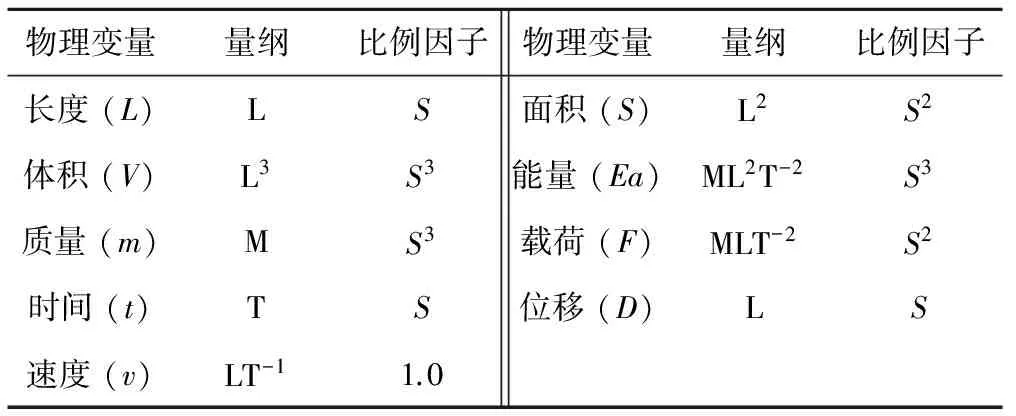
表1 部分比例因子

圖1為相似2節車輛，其質量、載荷及時間根據表1的相似系數進行縮放，則

( 2 )

根據牛頓第二定律，對于2個物體，分別有

( 3 )

( 4 )

將式( 2 )代入式( 3 )，得

( 5 )

對比式( 4 )和式( 5 )得

( 6 )

對于位移，有

( 7 )

然而，由于尺寸效應的存在，很難實現對摩擦力載荷的準確縮放，列車縱向動力學模型中摩擦力的表達式為

Ffi=Fn·μ

( 8 )

式中：Fn為法向力；μ為摩擦系數。列車縱向碰撞模型中，車體所受法向力(Fn)的大小等于車輛受到的重力mg。根據表1，質量(m)按照比例因子S3進行縮放，重力加速度(g)比例因子為1，即重力載荷同樣以比例因子S3進行縮放，而不是理論上要求的S2，因此重力載荷不能滿足相似性要求。為保證摩擦力載荷滿足相似性要求，必須對無量綱參數摩擦系數μ進行縮放，對于摩擦系數為0.1的一個原模型而言，在1/8比例的縮比模型中，它的摩擦系數達到了0.8，這是很難精確實現的。

列車縱向縮比模型研究的是列車碰撞在縱向上的運動，不涉及垂向上的重力載荷。但是，由重力載荷引起的縱向摩擦力載荷的尺寸效應是不容忽略的，必須研究摩擦系數對于列車碰撞能量耗散規律的影響，并采取一定的修正措施。

2 列車小比例縱向縮比模型碰撞試驗

以國內某主型8編組動車組為例，參考歐洲標準EN 15227[16]，碰撞場景選取條件為：一列8編組動車組以25 km/h速度與另一列相同8編組動車組發生正面碰撞。開展列車小比例模型試驗，車體簡化為質量按比例因子縮放的質量塊；緩沖器使用力學特性較為接近的橡膠元件代替；壓潰管和主吸能結構等吸能裝置采用受壓力值較為平穩的不同強度的蜂窩來代替，為避免壓縮過程中出現左右嚴重偏載情況，試驗過程中蜂窩一分為二并對稱分布在兩邊。

標準規定工況為8編組動車組的對撞，然而，將一個8編組動車組的縮比模型列車運動起來并達到一定的速度，是比較困難的，出于經濟成本考慮，對碰撞場景進行簡化設計，見圖2。使用一個質量與列車縮比模型相等的臺車來代替運動列車，保留運動列車前端的吸能結構。臺車前端的吸能結構與靜止列車縮比模型一同放在工裝的滑動軌道內，并同靜止列車模型的前端——圖2中的撞擊界面對稱。

根據文獻[14]，列車在碰撞過程中的變形及吸能主要集中在頭車和次節車，次節車以后各結構的變形量較小。因此，對于整列車縮比模型的設計，做了進一步合理簡化，省去了2車以后車輛間的車體載人區蜂窩以及部分壓潰管吸能蜂窩，見圖2。碰撞界面1布置為左右對稱的頭部吸能結構，從中間往兩邊分別為橡膠緩沖器、壓潰管和主吸能結構；碰撞界面2的吸能結構布置為左右對稱的中間車鉤橡膠緩沖器、壓潰管和車體承載區；碰撞界面3及其以后碰撞界面僅布置單個緩沖器和壓潰管。結合試驗場所的實際情況，本次列車縮比試驗采用1/8比例模型，縮比試驗模型的詳細參數見表2。

表2 縮比模型設計

試驗場景見圖3。試驗過程中，臺車經加速裝置加速到25 km/h速度后，沿平直軌道運動。實測臺車剛開始接觸靜止蜂窩時的撞擊速度為23.4 km/h(6.499 m/s)，比設定值(25 km/h)略低，這是臺車運動過程中輪軌磨耗引起的。圖4給出了通過高速攝影捕捉到的撞擊試驗前、試驗中及試驗后的場景。

表3列出了試驗過程中各位置蜂窩的最大變形量，由于橡膠元件的變形量難以測量且吸能量較少，因此在這里不予考慮。碰撞界面2以后的撞擊界面吸能蜂窩沒有發生變形，表中沒有一一列出。圖5為各車輛的速度曲線，由于高速攝影儀的拍攝范圍所限，因此重點拍攝了運動臺車和靜止1～5車的運動過程。

表3 各蜂窩的壓縮量及吸能量

3 摩擦系數對列車能量耗散的影響規律

基于動力學軟件ADAMS，建立列車縱向碰撞的原模型，模擬臺車對8編組動車組的碰撞過程。在列車質量分布、碰撞速度及列車端部吸能結構保持不變的條件下，分別改變臺車和8編組動車組摩擦系數的大小，研究不同摩擦系數下列車碰撞各撞擊界面吸能規律。開展5種不同摩擦系數(0、0.06、0.16、0.26和0.36)下臺車對8車編組的動車組碰撞仿真計算，共計25種工況，碰撞速度與試驗速度保持一致。表4為運動臺車摩擦系數等于0.36時對應的各碰撞界面最大壓縮量隨8編組動車組摩擦系數變化的計算結果，其中μ1為運動臺車摩擦系數，μ2為靜止8編組動車組的摩擦系數。

由表4可知，在臺車對8編組動車組的碰撞過程中，能量吸收主要集中在頭車碰撞界面，其他碰撞界面的能量耗散相對較小，因此本文接下來主要研究摩擦系數對頭部碰撞界面壓縮量(D)的影響。

圖6為在不同的μ1下，D隨μ2的變化規律，圖7為μ1=μ2時，D隨摩擦系數的變化規律曲線。由圖6、圖7可知，摩擦系數對于車輛碰撞過程中的能量耗散有著十分重要的影響。靜止8編組動車組的摩擦系數越大，頭車碰撞界面的最大壓縮量也越大；運動臺車的摩擦系數越大，頭車碰撞界面的最大壓縮量越小；當運動臺車與靜止8編組動車組的摩擦系數一致時，頭車碰撞界面的最大壓縮量隨摩擦系數的增加而增加。增加動車的摩擦系數，減小靜止車的摩擦系數可以有效減緩車輛發生碰撞時的破壞程度，且從總體上而言，摩擦系數的增加起到減緩碰撞的作用。

表4 μ1=0.36時，各撞擊界面的最大壓縮量 mm

4 摩擦系數間的相互轉化關系

根據上述分析，在列車縱向碰撞模型中，摩擦系數的影響是不容忽視的，對于摩擦系數難以精確縮比的情況，必須根據實際情況加以修正。

采用最小二乘法對動力學仿真計算得到樣本點進行擬合，得到頭車碰撞界面最大壓縮量D隨μ1、μ2變化的三階響應曲面，見圖8。響應面的具體表達式為

D=4.216-9.393×μ1+6.715×μ2+

( 9 )

表5為最小二乘法的擬合質量，由表5可知，響應面模型的判定系數在0.98以上，認為響應面模型的精度達到要求。為進一步驗證模型的擬合精度，通過拉丁超立法采樣方法隨機生成5個樣本點，動力學仿真計算結果同響應面擬合結果對比見表6，最大相對誤差為5.35%。

表5 最小二乘法擬合質量

表6 響應面模型驗證

1/8小比例模型試驗中，試驗臺車與軌道間為滾動摩擦，摩擦系數取0.12，模型與工裝軌道間為滑動摩擦，摩擦系數取0.17(鋁和鋼的滑動摩擦系數為0.17)。對應的實車模型中，為保證摩擦力載荷滿足相似性要求，摩擦系數應除以相應的比例因子，得到1∶1比例實車仿真計算下運動車的摩擦系數為0.015，靜止車的摩擦系數為0.021。由表達式( 9 )獲取的D值(減去緩沖器長度)與列車小比例模型試驗結果進行對比，見表7。

表7 響應面擬合值同試驗結果對比

由表7可知，響應面得到的頭車碰撞界面最大壓縮量與列車小比例模型試驗轉換過來的結果吻合較好，相對誤差為8.85%，說明響應面模型是可靠的。

這對縮比模型試驗具有非常重要的作用，因為按照現有理論，將小比例縮比模型試驗的試驗數據還原處理后，得到的都是摩擦系數較小工況下列車碰撞結果，這并不是真實的碰撞情況。而通過相應的響應面模型，可以獲取真實摩擦系數下列車碰撞界面最大壓縮量和吸能量。

取μ1=0.015、μ2=0.021，開展相應的動力學仿真計算，得到的車輛速度變化曲線同列車小比例碰撞試驗轉換成實車后的試驗數據進行比較。圖9分別為臺車及1～5車的速度曲線。

5 結論

(1) 通過不同摩擦系數下，運動臺車對靜止8編組動車組的碰撞仿真，得到了摩擦系數對列車碰撞過程中能量耗散的影響規律。研究結果表明，在列車縱向碰撞模型中，摩擦系數的影響是不容忽略的。增加運動車的摩擦系數，減小靜止車的摩擦系數可以有效減緩車輛發生碰撞時的破壞程度，且從總體而言，摩擦系數的增加可以減緩碰撞過程。動力學仿真結果與試驗結果吻合較好，說明采用動力學計算來分析摩擦系數對列車耗能規律的影響是可靠的。

(2) 采用最小二乘法對動力學仿真計算的樣本點進行擬合，得到了頭部碰撞界面最大壓縮量D隨μ1、μ2變化的三階響應曲面。針對列車縱向碰撞模型縮放過程中，摩擦系數難以精確縮比的情況，利用該響應面模型可以實現不同摩擦系數間的相互轉化，對列車小比例模型試驗有著十分重要的意義。

(3) 開展列車1/8比例模型縱向碰撞試驗，頭部碰撞界面最大壓縮量的響應面擬合結果與小比例試驗結果吻合較好，相對誤差為8.86%，證明該響應面模型是可靠的，研究結果可用于指導列車小比例碰撞試驗。

參考文獻：

[1] 田紅旗, 許平. 吸能列車與障礙物撞擊過程的研究和分析[J]. 長沙鐵道學院學報, 2002, 20(3):55-60.

TIAN Hongqi, XU Ping. Analysis of Collision between Energy-absorbing Train and Barrier[J]. Journal of Changsha Railway University, 2002, 20(3):55-60.

[2] 張在中, 姚曙光. 城市軌道車輛吸能結構設計[J]. 鐵道科學與工程學報, 2013, 10(3):94-98.

ZHANG Zaizhong, YAO Shuguang. Design of Energy Absorption Structure for Urban Track Vehicle[J]. Journal of Railway Science and Engineering, 2013, 10(3):94-98.

[3] 謝素超, 周輝. 基于Kriging法的鐵道車輛客室結構優化[J]. 中南大學學報(自然科學版), 2012, 43(5):1990-1998.

XIE Suchao, ZHOU Hui. Optimization on Passenger Compartment Structure of Railway Vehicle Based on Kriging Method[J]. Journal of Central South University (Science and Technology), 2012, 43(5):1990-1998.

[4] 李健, 高廣軍, 董海鵬, 等. 帶隔板薄壁方管的耐撞性研究[J]. 中南大學學報 (自然科學版), 2014, 45(7):2481-2488.

LI Jian, GAO Guangjun, DONG Haipeng, et al. Research on Crashworthiness of Thin-walled Square Tubes with Diaphragms[J]. Journal of Central South University (Science and Technology), 2014, 45(7):2481-2488.

[5] 楊超, 朱濤, 肖守訥. 列車車體鋁合金動態力學性能及其對吸能的影響[J]. 中南大學學報 (自然科學版), 2015, 46(7):2744-2749.

YANG Chao, ZHU Tao, XIAO Shoune. Dynamic Mechanical Properties of Aluminum Alloy Used in Carbodies of Trains and Effect on Energy Absorption[J]. Journal of Central South University (Science and Technology), 2015, 46(7):2744-2749.

[6] 常寧, 劉國偉. 軌道車輛切削式吸能過程仿真[J]. 中南大學學報(自然科學版), 2010, 41(6):2444-2450.

CHANG Ning, LIU Guowei. Simulation for Energy- absorbing Process of Railway Vehicle in Metal-cutting Way[J]. Journal of Central South University (Science and Technology), 2010, 41(6):2444-2450.

[7] TABRI K, VARSTA P, MATUSIAK J. Numerical and Experimental Motion Simulations of Nonsymmetric Ship Collisions[J]. Journal of Marine Science and Technology, 2010, 15(1):87-101.

[8] TABRI K, MATUSIAK J, VARSTA P. Sloshing Interaction in Ship Collisions—An Experimental and Numerical Study[J]. Ocean Engineering, 2009, 36(17):1366-1376.

[10] LOWE W T, AL-HASSANI S T S, JOHNSON W. Impact Behaviour of Small Scale Model Motor Coaches[J]. Proceedings of the Institution of Mechanical Engineers, 1972, 186(1):409-419.

[11] XU L J, LU X Z, SMITH S T, et al. Scaled Model Test for Collision Between Over-height Truck and Bridge Superstructure[J]. International Journal of Impact Engineering, 2012, 49(3):31-42.

[12] ZHU H, YANG Z. Numerical study on scale of high speed train model for wind tunnel testing[C]//IEEE Electrical and Control Engineering (ICECE), 2011 International Conference on. New York: IEEE, 2011:725-728.

[13] DIAS J P, PEREIRA M S. Optimization Methods for Crashworthiness Design Using Multibody Models[J]. Computers and Structures, 2004, 82(17):1371-1380.

[14] LU G.Energy Absorption Requirement for Crashworthy Vehicles[J]. Proceedings of the Institution of Mechanical Engineers, Part F:Journal of Rail and Rapid Transit, 2002, 216(1):31-39.

[15] 余同希, 盧國興, 華云龍. 材料與結構的能量吸收[M]. 北京:化學工業出版社, 2006:50-58.

[16] CEN. EN 15227-2011 Railway applications-Crashworthiness requirements for railway vehicle bodies[S]. German:DE-DIN, 2011.