有軌電車荷載作用下路基應(yīng)力響應(yīng)分析

王浩然

(1.上海市城市建設(shè)設(shè)計研究總院(集團)有限公司,上海 200125; 2.同濟大學(xué)地下建筑與工程系,上海 200092)

0 引 言

隨著國民經(jīng)濟的迅猛發(fā)展,城市建設(shè)日新月異,隨著國民生活水平的不斷提高,私人汽車的保有量不斷增加,然而隨后由此引發(fā)了一系列環(huán)境問題,頻頻出現(xiàn)的霧霾天氣,堅定了國家對大氣污染堅決治理的決心。有軌電車具有高效、安靜、環(huán)保等優(yōu)點,近些年來越來越受到各地區(qū)的關(guān)注。我國現(xiàn)代有軌電車尚屬起步階段,缺乏相對應(yīng)的規(guī)范來指導(dǎo)設(shè)計,目前只能參照普通鐵路、地鐵等相關(guān)規(guī)范。在已有的工程項目設(shè)計中,設(shè)計人員發(fā)現(xiàn)有軌電車荷載水平明顯要低于傳統(tǒng)地鐵和鐵路等交通動載,前者在運營期的運行速度要明顯低于后者。因此,理論上有軌電車荷載作用于地基產(chǎn)生的動應(yīng)力擴散效應(yīng)與鐵路路基相比將有顯著的差異性。本文將采用三維顯式動力有限元,對有軌電車應(yīng)力響應(yīng)特性及傳播機理進行分析。

1 有軌電車基本參數(shù)

1.1 路基基床參數(shù)

有軌電車路基采用整體道床結(jié)構(gòu),其標(biāo)準(zhǔn)橫斷面如圖1所示,基床中各結(jié)構(gòu)層材料參數(shù)如表1所示。至于地基土材料參數(shù),根據(jù)連續(xù)介質(zhì)理論,地基土采用彈性材料不會給應(yīng)力計算帶來太大的誤差。上海第③層土的壓縮模量為2.2～5.9 MPa[1],取平均值4 MPa。有限元程序中需要輸入的土層模量是彈性模量,彈性模量可取壓縮模量的6.5倍[2]。

圖1 有軌電車路基標(biāo)準(zhǔn)橫斷面(單位:mm)Fig.1 Subgrade standard cross section of tramcar (Unit:mm)

表1基床材料參數(shù)

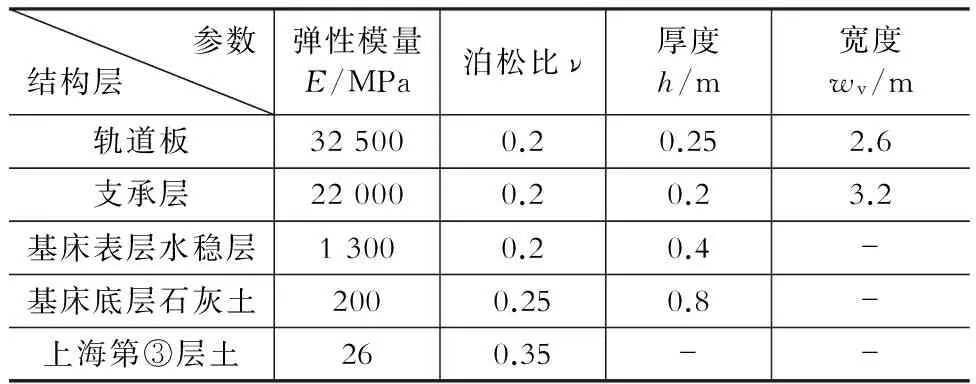
Table 1 Material parameters of subgrade bed

1.2 車輛及軌道參數(shù)

有軌電車車輛軸距1.7 m,定距11.1 m,滿載軸重12.5 t,設(shè)計速度70 km/h。軌道板上下行分開,單塊軌道板寬2.6 m、長12.5 m、厚0.25 m,采用C40鋼筋混凝土板,軌道扣件間距0.6 m,車輛模型如圖2所示。

2 模型建立

2.1 荷載施加

對于整體道床可認(rèn)為輪軌荷載由5個彈性扣件承擔(dān),分擔(dān)比為0.1,0.2,0.4,0.2,0.1,并經(jīng)彈性扣件傳遞至軌道板,當(dāng)考慮臨近輪軸的影響時,如圖3所示,縱向分布總長度4.1 m。荷載橫向分布范圍等于軌道板寬度2.6 m。

輪軌荷載可以以半正弦波脈沖表示[3],如公式(1)所示。

p(t)=Psin2(2πft)

(1)

式中,p(t)為輪載;P為輪載峰值;f為荷載作用頻率。

輪載峰值P可以根據(jù)經(jīng)驗公式計算[4],如公式(2)所示。

P=P靜(1+0.003v)

(2)

式中,P為輪載峰值;P靜為靜輪載;v為速度,km/s。

荷載作用頻率f可以根據(jù)車輛定距11.1 m及行車速度v求得,不同行車速度所對應(yīng)的荷載頻率如表2所示。

表2荷載頻率

Table 2 Loading frequency

整體道床結(jié)構(gòu)假設(shè)路基面荷載均勻分布,如圖4所示,因此每對輪軸下的軌道板豎向荷載為

圖4 荷載分布Fig.4 Load distribution

以上所述的有軌電車移動半正弦波荷載可以通過VDLOAD用戶子程序的二次開發(fā)實現(xiàn)。

2.2 建模

1) 人工邊界選取

采用有限元模擬靜力問題時,只需要保證邊界與所關(guān)心的區(qū)域足夠遠(yuǎn)即可忽略邊界效應(yīng)對結(jié)果的影響。但是進行動力問題模擬時,應(yīng)力波會在邊界處發(fā)生虛擬反射,為了避免應(yīng)力波反射,需要設(shè)置人工邊界條件。ABAQUS 顯式分析模塊基于Zienkiewicz[5]的無限元理論及Lysmer[6]的黏性理論創(chuàng)立了無限元人工邊界。在建模中,無限元的節(jié)點排列是有特定要求的,它必須按照逆時針的規(guī)律進行排序,而且單元的第一個面要求是有限元和無限元的交界面,如圖5所示。無限元的延伸反向不能交叉,圖6給出了正確和錯誤的無限元示例[7]。

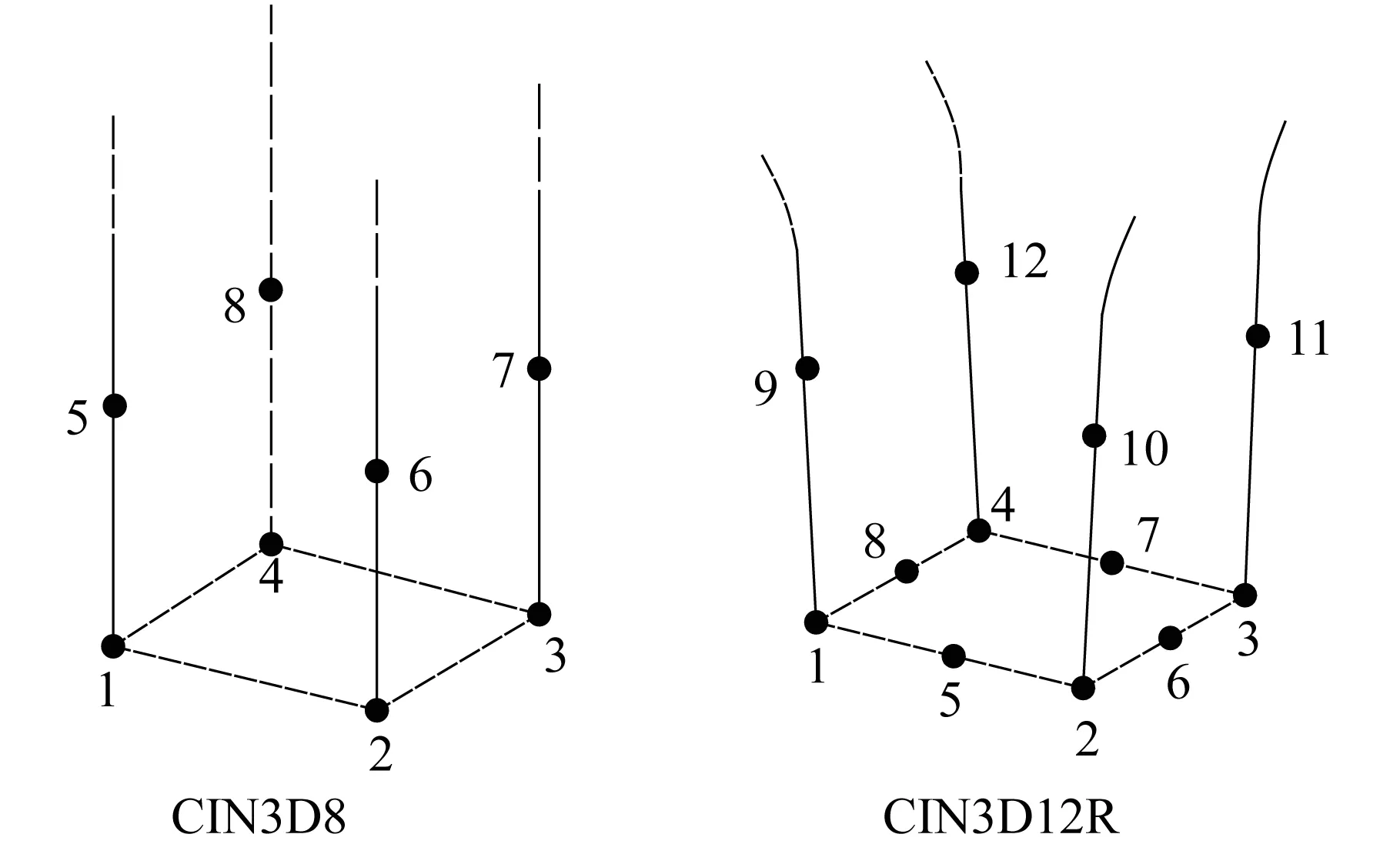
圖5 無限元節(jié)點編號規(guī)則Fig.5 Arrangement rules of infinite element nodes

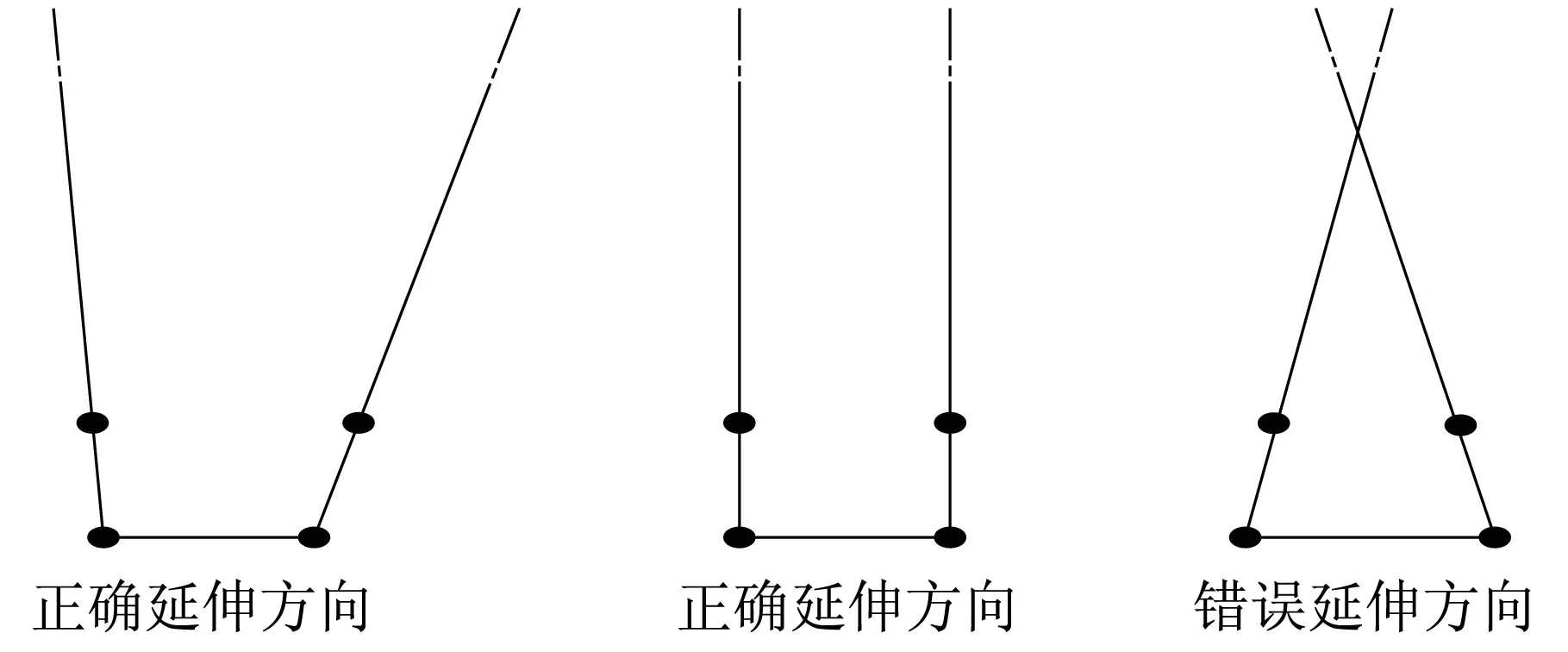
圖6 無限元延伸方向Fig.6 Extending direction of infinite element

2) 模型幾何形狀

要保證對邊界處的應(yīng)力波具有良好吸收效果,一方面需要選取合適的人工邊界,另一方面需要建立合適的幾何模型。當(dāng)應(yīng)力波以不同的入射角入射到人工邊界時,人工邊界吸收效果會有差異[8]。Connolly建立了拉長的球形模型[9],使得移動荷載激起的應(yīng)力波能最大限度地以較優(yōu)入射角的方式進入邊界,從而提高了人工邊界的吸收效果。

直接在Abaqus建立拉長半球形模型時,邊界處無限元單元節(jié)點號無法按程序所要求的順序進行排列,對此本文采用Matlab軟件編制無限元節(jié)點生成程序,使得模型節(jié)點能按Abaqus軟件的要求進行排列。綜合以上所述,可以建立有限元模型及相應(yīng)網(wǎng)格分別如圖7和圖8所示。

3 計算結(jié)果

3.1 正常運營速度下路基應(yīng)力響應(yīng)

有軌電車的最高運行速度是70 km/h,一般來說,實際的運行速度會保持在25 km/h左右。由圖9、圖10可知,荷載經(jīng)過引起的附加豎向應(yīng)力σz隨深度增加,其幅值迅速衰減,在深度0.7 m的位置,附加應(yīng)力衰減了50%。對于荷載駛近與駛離時,荷載移動帶下方各點經(jīng)受了3次半正弦波荷載的激振,因此在進行路基鋪筑時,需要更加注意上中墊層的壓實質(zhì)量,并提高其疲勞強度。根據(jù)相應(yīng)《上海市建筑地基基礎(chǔ)設(shè)計》中軟土地基中附加應(yīng)力占自重應(yīng)力的10% 的判斷標(biāo)準(zhǔn),可求得動應(yīng)力影響深度約2.9 m。

圖7 三維有限元模型Fig.7 Three-dimensional finite element model

圖8 網(wǎng)格劃分Fig.8 Finite element mesh

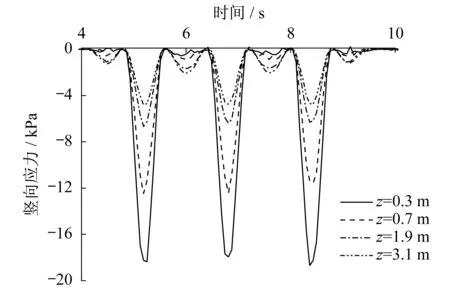
圖9 豎向應(yīng)力σz隨時間變化規(guī)律Fig.9 Vertical stress σz vs time

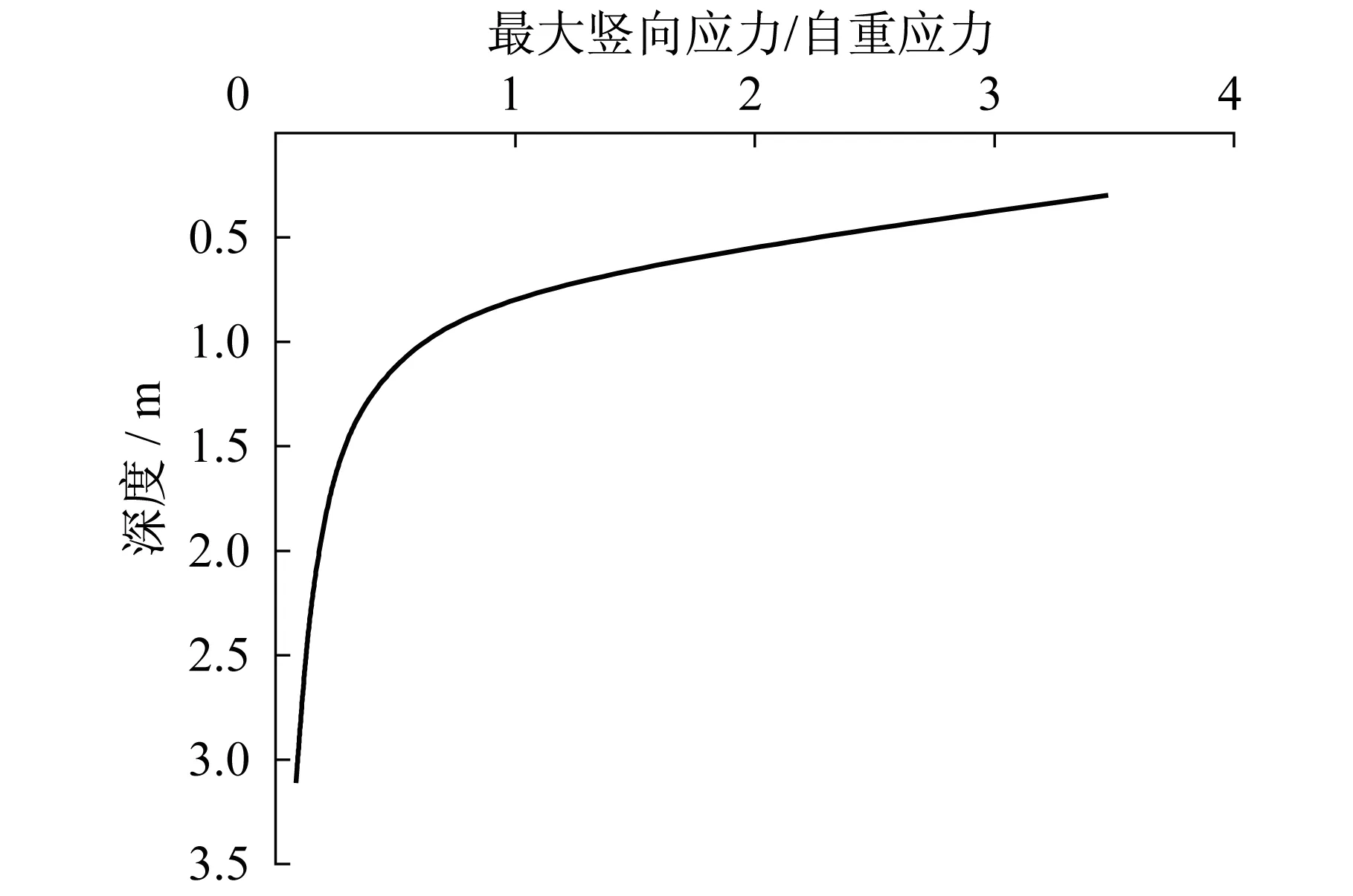
圖10 最大豎向應(yīng)力隨深度變化規(guī)律Fig.10 The maximum vertical stress vs depth

3.2 運營速度對路基應(yīng)力響應(yīng)的影響

考慮到有軌電車不會一直以恒定速度運行,不同路段或運營工況下,其運營速度會發(fā)生變化,最高運營速度可達到70 km/h。本節(jié)將對速度與應(yīng)力響應(yīng)之間的關(guān)系進行分析。由圖11可知,不同速度下豎向附加應(yīng)力隨深度的衰減規(guī)律基本相同,隨著速度的增加,應(yīng)力的影響深度不斷加大,以軟土地基中附加應(yīng)力等于自重應(yīng)力10%的標(biāo)準(zhǔn)判斷,運營速度從10 km/h到70 km/h變化時,應(yīng)力影響深度從2.8 m增加到3.2 m。有軌電車以最大運營速度為70 km/h,此速度下應(yīng)力影響深度達到3.2 m,地基沉降計算深度或地基處理設(shè)計深度可以參照此深度進行。

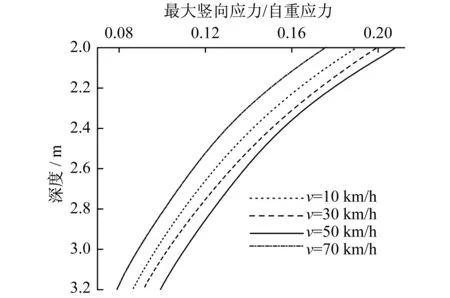
圖11 不同速度下最大豎向應(yīng)力隨深度變化規(guī)律Fig.11 The maximum vertical stress vs depth at different speed

4 結(jié) 論

(1) 荷載經(jīng)過引起的附加豎向應(yīng)力σz隨深度增加,其幅值迅速衰減,在深度0.7 m的位置,附加應(yīng)力衰減了50%。每運行一次路基下方個點都經(jīng)受了3次半正弦波荷載的激振,因此要提高上中墊層的壓實質(zhì)量保證抗疲勞強度。以附加應(yīng)力占自重應(yīng)力的10% 的標(biāo)準(zhǔn),該速度下動應(yīng)力影響深度約2.9 m。

(2) 附加動應(yīng)力峰值及影響深度與運營速度存在正相關(guān)的關(guān)系,當(dāng)有軌電車達到最大運營速度70 km/h時,動應(yīng)力影響深度為3.2 m,該值可作為路基沉降計算深度及地基處理深度的參考值。

[1] 37-2012 D G J.上海市巖土工程勘察規(guī)范 [S]].出版社,2002.

37-2012 D G J.Code for investigation of geotechnical engineering[S].Location,Press,2012.(in Chinese)

[2] 中國振動工程學(xué)會土動力學(xué)專業(yè)委員會.土動力學(xué)工程應(yīng)用實例與分析[M].北京:中國建筑工業(yè)出版社,1998:193-200.

Special Committee of Soil Dynamics,Chinese Society for Vibration Engineering.Applications and analyses of soil dynamics in engineering[M].Beijing:China Architecture & Building Press,1998:193-200.(in Chinese)

[3] 薛富春,張建民.移動荷載作用下高速鐵路軌道-路基-地基耦合系統(tǒng)振動加速度的空間分布特征[J].巖土工程學(xué)報,2014,12:2179-2187.

Xue Fuchun,Zhang Jianmin.Spatial distribution of vibration accelerations in coupled rail-embankment foundation system on high-speed railway under moving loads[J].Chinese Journal of Geotechnical Engineering,2014,36(12):2179-2187.(in Chinese)

[4] 屈曉輝,崔俊杰.客運專線鐵路路基設(shè)計技術(shù)[M].北京:人民交通出版社,2008.

Qu Xioahui,Cui Junjie.Design technology of railway subgrade for passenger dedicated line[M].Beijing:China Communications Press,2008.(in Chinese)

[5] Zienkiewicz O C,Emson C,Bettess P.A novel boundary infinite element[J].International Journal for Numerical Methods in Engineering,1983,19(3):393-404.

[6] Lysmer J.Finite dynamic model for infinite media[C]Proc.of ASCE,1969:859-877.

[7] 費康,張建偉.ABAQUS 在巖土工程中的應(yīng)用[M].北京:中國水利水電出版社,2010.

Fei Kang,Zhang Jianwei.Application of ABAQUS in geotechnical engineering [M].Beijing:China Water Power Press,2010.(in Chinese)

[8] Kouroussis G,Van Parys L,Conti C,et al.Using three-dimensional finite element analysis in time domain to model railway-induced ground vibrations[J].Advances in Engineering Software,2014,70:63-76.

[9] Connolly D,Giannopoulos A,Forde M C.Numerical modelling of ground borne vibrations from high speed rail lines on embankments[J].Soil Dynamics and Earthquake Engineering,2013,46:13-19.