柱截面變化對框架結構現澆板受力性能的影響研究

賈傳果 胡鵬飛 張付杰

(1.山地城鎮建設與新技術教育部重點實驗室,重慶 400045; 2.重慶大學土木工程學院,重慶 400045)

0 引 言

我國現行混凝土結構設計規范規定,在樓板角部宜沿兩個方向正交、斜向平行或放射狀布置附加鋼筋。對于小截面柱而言,此法可以有效地控制樓板柱角處裂縫。對于高層或超高層建筑的下部樓層,隨著總層數的增加,柱(主要承受其上所有樓層的豎向荷載)截面越來越大,而梁(主要承受其上一層的樓面荷載)截面變化不大,這使得對應的樓板更接近于異形板。這種情況下,樓板的計算和配筋往往還沿用單向板或雙向板的設計方法和構造要求,忽略異形板受力尤其是應力分布上的特殊性。在異形樓板轉角處易出現應力集中[1-3],也容易出現板的脆性沖切破壞[4],從而導致樓板開裂。

為此,本文結合實際工程,采用ANSYS軟件進行大截面柱框架結構樓板的數值模擬。從樓板主拉應力、彎矩、屈服線以及開裂程度等方面,探討在豎向荷載作用下柱截面變化對樓板的影響,為大截面柱框架結構樓板的設計及構造措施提供一定的參考。

1 豎向荷載作用下樓板受力性能分析

1.1 算例

本文設計了一層3×3跨框架結構模型,如圖1所示,跨度(L)為4 800 mm,層高為3 000 mm,梁高500 mm,梁寬250 mm,柱截面寬度(C)為500～1 800 mm。

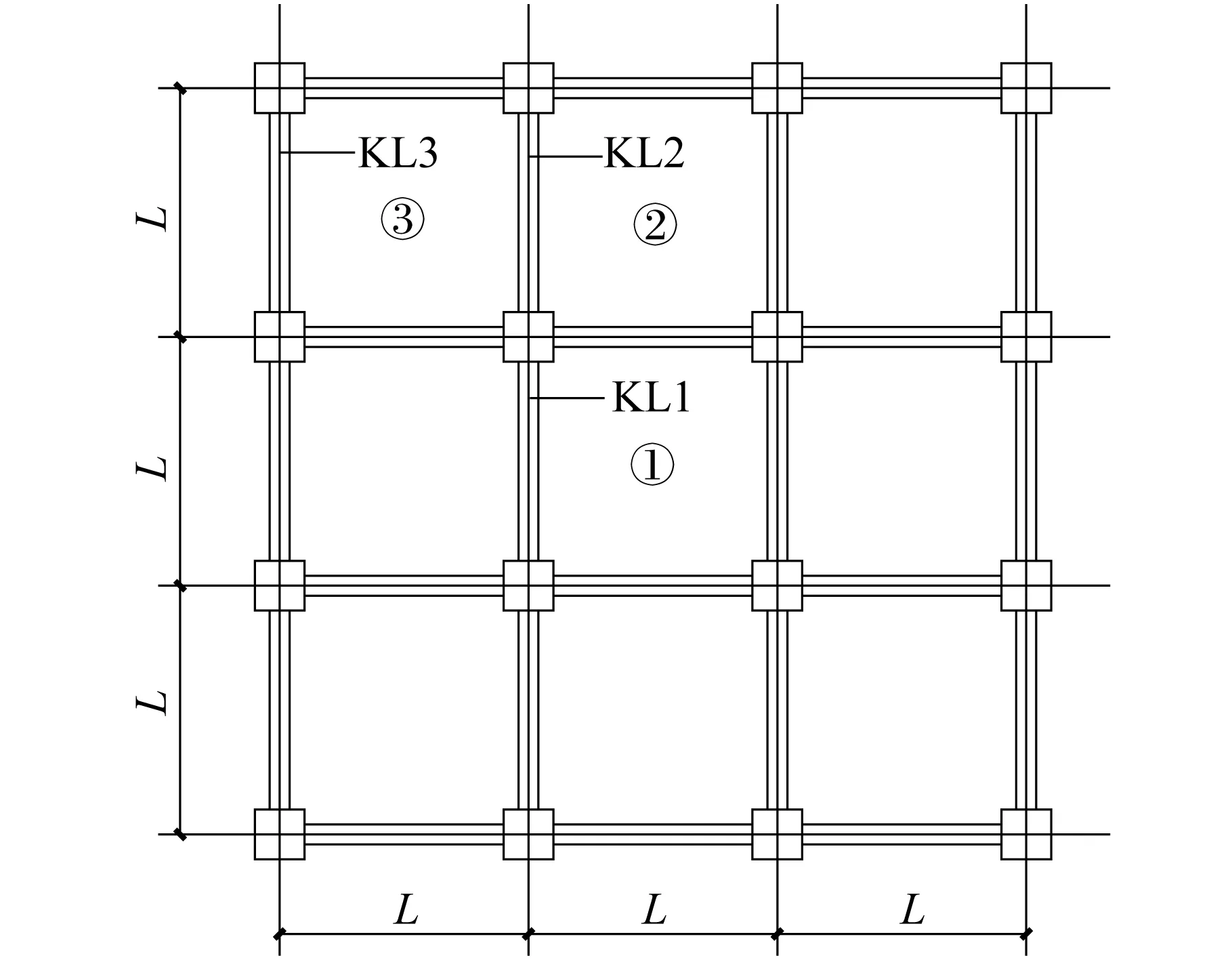
圖1 模型平面圖Fig.1 Model layout

本節涉及到工程中常用的三種板格,具體如下:內板格,如圖1中板①所示;邊板格,如圖1中板②所示;角板格,如圖1中板③所示。另外,實際工程中還涉及多種荷載布置形式[1]。本文討論三種,分別為滿布荷載、棋狀荷載1、棋狀荷載2,如圖2所示。

本文采用ANSYS軟件進行樓板的受力性能分析[5]。鋼筋采用Link8單元,鋼筋為HRB400級鋼筋,泊松比為0.3;混凝土采用Solid65單元,強度等級為C30,泊松比為0.2。后文裂縫分析(包括2.5節樓板屈服線、3節的大截面柱框架結構實際工程分析和4節的樓板構造措施探討)采用如圖3所示的混凝土和鋼筋本構關系,其余均進行彈性分析,混凝土彈性模量取3×104MPa,鋼筋彈性模量取2×105MPa。除自重外,還考慮3 kN/m2的豎向荷載。

圖2 荷載布置形式Fig.2 Load arrangement

圖3 材料本構模型Fig.3 Material constitutive model

1.2 柱角處樓板主拉應力

后文中所提到的實際工程中,柱角處樓板的開裂較嚴重,故首先分析柱角處樓板的主拉應力。為反映柱截面大小對板受力的影響,本文引入柱跨比,即柱截面寬度C和板跨度L的比值。圖4-圖6分別為內板格、邊板格和角板格在三種不同荷載布置形式下的柱角處主拉應力隨柱跨比的變化規律。可以看出,柱角處主拉應力先隨著柱跨比的增加而增加。其原因在于,隨柱截面的增大,柱對樓板的約束加強,樓板上的荷載部分直接傳給柱。

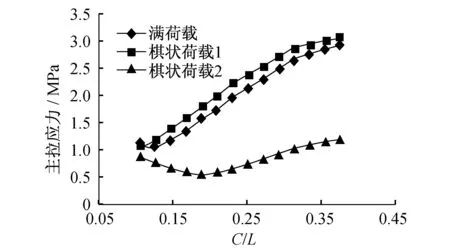
圖4 內板格板頂柱角處主拉應力Fig.4 Principal tensile stress of inner slab

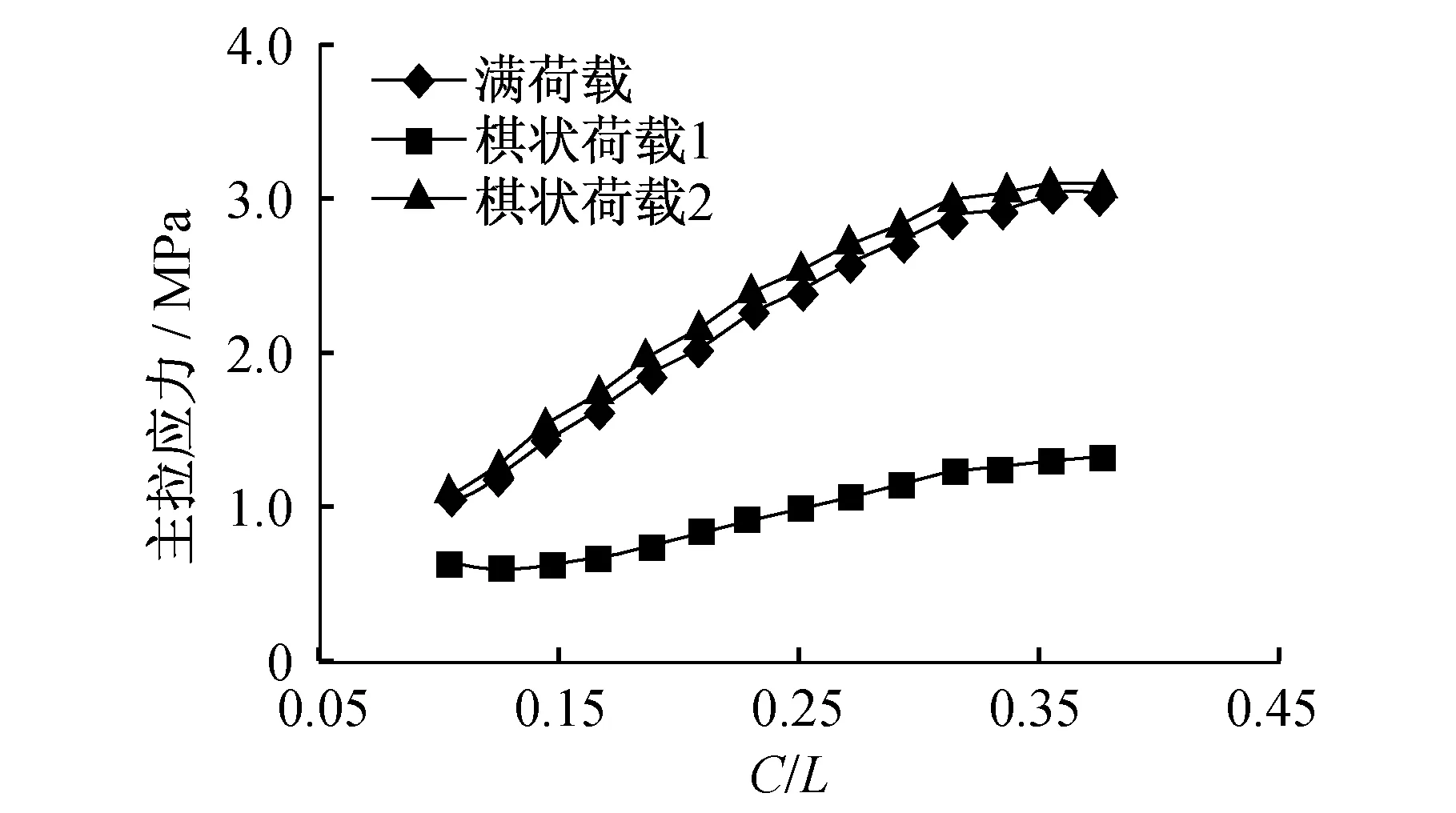
圖5 邊板格板頂柱角處主拉應力Fig.5 Principal tensile stress of side slab

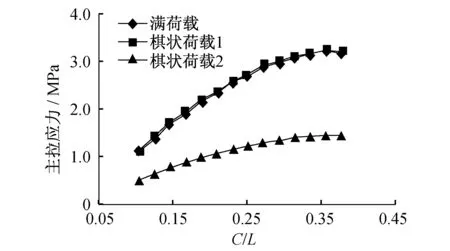
圖6 角板格板頂柱角處主拉應力Fig.6 Principal tensile stress of corner slab

1.3 板頂主拉應力

圖7和圖8分別給出小柱截面(以500 mm柱截面為例)和大柱截面(以1 800 mm柱截面為例)框架結構樓板在棋狀荷載1作用下的板頂主拉應力分布圖。對比發現,柱截面的增大對板頂主拉應力分布影響較大;柱截面較小時,梁邊主拉應力最大;柱截面較大時,柱角處主拉應力最大,且受力集中現象更嚴重。

圖7 小截面柱板頂主拉應力Fig.7 Slab principal tensile stress of slender column

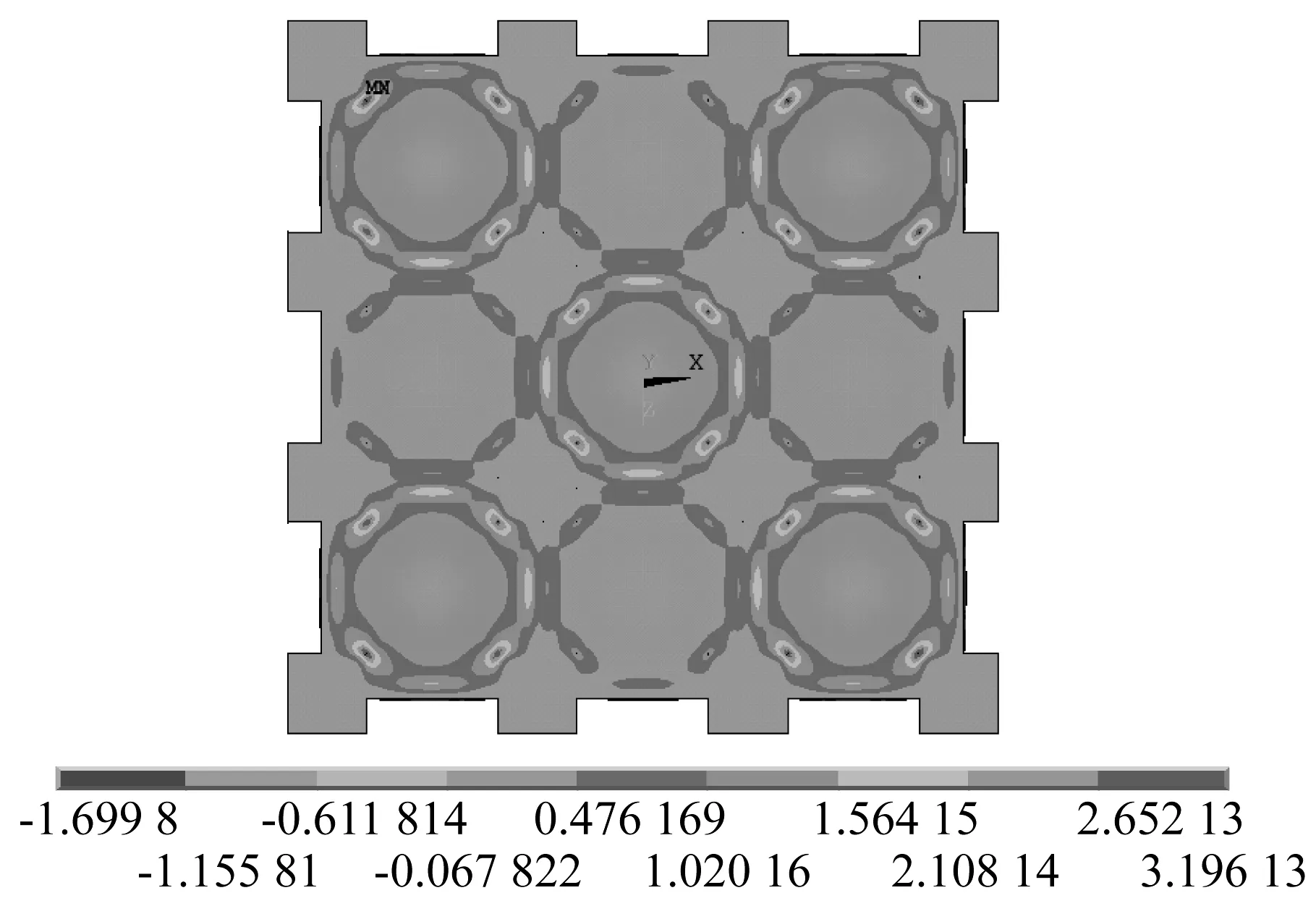
圖8 大截面柱板頂主拉應力Fig.8 Slab principal tensile stress of fat column

比較圖7和圖8,可見內格板的板頂主拉應力差距明顯且具有代表性。圖9給出了內板格在柱角處和梁跨中處的板頂主拉應力隨柱跨比的變化規律。可以看出,隨柱跨比的增加,梁跨中附近內板格板頂主拉應力減小;柱角處板頂主拉應力隨之增加;在柱跨比約為0.25處兩線相交。可見,隨著柱跨比的增加,樓板板頂裂縫控制重點從梁邊轉到柱角處。

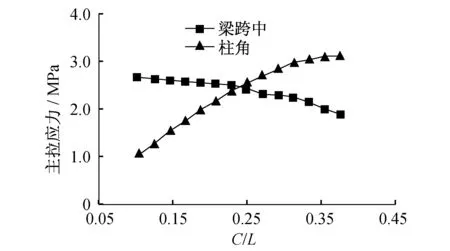
圖9 內板格板頂主拉應力Fig.9 Principal tensile stress of inner slab

1.4 樓板彎矩

為簡化計算,本節僅考慮內格板,且采用雙向均為單跨的框架結構為研究對象,其1/4模型如圖10所示。具體尺寸如下:跨度(L)采用4 800 mm,層高為3 000 mm,梁截面為300 mm×500 mm (梁的寬度變大主要為實現內板格的邊界約束),柱截面(C)在600～1 600 mm之間變化,板厚為120 mm。板采用雙層雙向10@150鋼筋,梁受拉和受壓區均為6根22的鋼筋,箍筋為10@100,框架柱配筋率為2%,鋼筋均為HRB400級鋼。

圖10 有限元計算模型Fig.10 The FE analysis model

本節考慮了板對角線上26個節點和板跨中線29個節點上50 mm寬板帶的彎矩,其中節點位置如圖11所示,分析板帶彎矩隨離柱角的距離和柱跨比的變化規律(圖12和圖13)。

圖11 節點示意圖Fig.11 Schematic drawing of nodes

從圖12可以看出,同一柱截面下,板帶彎矩從柱角負彎矩增大至板中心正彎矩;隨柱截面增大柱角處負彎矩先增大后減小,板中心正彎矩一直減小,反彎點(零彎矩點)逐漸向板中心偏移。從圖13可以看出,同一柱截面下,板帶彎矩從梁跨中處負彎矩增大至板中心正彎矩;隨柱截面增大梁跨中處板的負彎矩和板中心正彎矩均有減小趨勢,反彎點在板跨中線上基本固定不變。

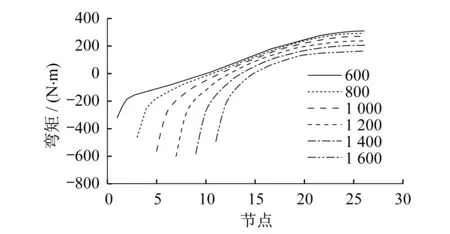
圖12 對角線上板帶彎矩Fig.12 Strip bending moment at diagonal line

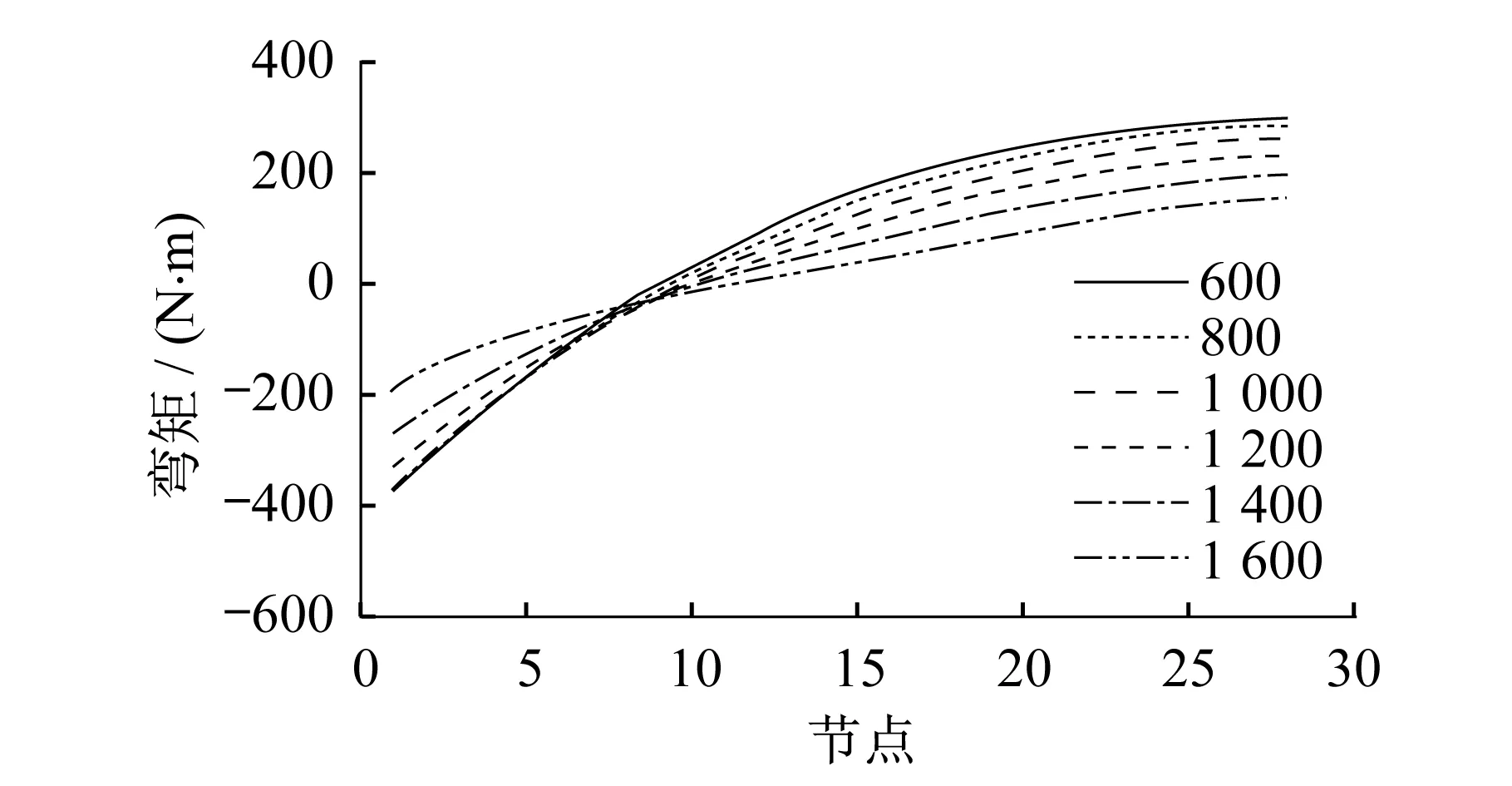
圖13 跨中板帶彎矩Fig.13 Strip bending moment at slab center line

分析圖12和圖13,可以繪制出板的零彎矩線,如圖14所示。《混凝土結構設計規范》(GB 50010—2010)第9.1.4條規定,支座負彎矩鋼筋向跨內延伸的長度應根據負彎矩圖確定,并滿足鋼筋錨固要求。從圖中可以看出,當柱截面較小時,按照矩形板的負彎矩圖來確定支座負彎矩鋼筋的延伸長度,可以覆蓋圖中的負彎矩區域;但柱截面較大時,按矩形板配筋無法覆蓋整個負彎矩區域。因此,對于大截面柱框架結構樓板,需適當增大支座負彎矩鋼筋的延伸長度。

1.5 樓板屈服線

樓板在開裂以前荷載較小時,彎矩是按照彈性平板理論分布的。開裂以后,彎矩分布由于開裂截面處抗彎剛度減小而產生了變化。隨著進一步加載,在最大彎矩的截面上出現了受拉鋼筋的屈服,板在屈服截面上會形成很大的曲率變化,同時,相應的彎矩實際上維持在極限抵抗彎矩上不變。再進一步加載,板會出現大的彎矩重分布。當板荷載繼續增大時,從最先屈服的那一點開始,直到由足夠數量的屈服點形成屈服線。這些屈服線把板分為許多板塊,并最終形成破壞機構。形成破壞機構的屈服線體系通常稱為屈服線模式[1]。通常,板四邊固結的雙向板在均布荷載作用下的屈服線如圖15所示。

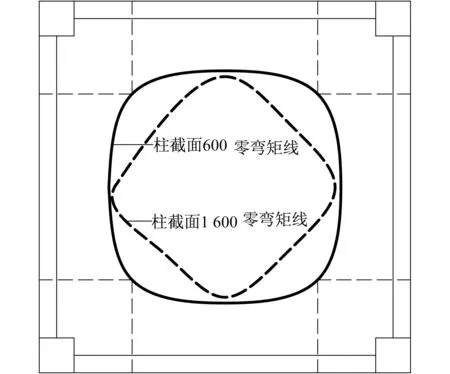
圖14 零彎矩線示意圖Fig.14 Schematic of the zero bending line

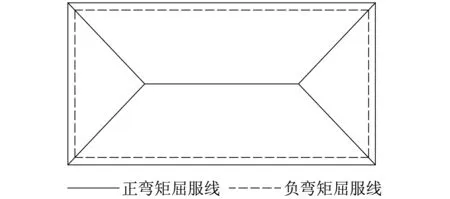
圖15 屈服線示意圖Fig.15 Schematic of the yield line

本節用ANSYS建立兩種非線性工況,研究樓板屈服線隨柱截面變化情況。工況一:柱截面為600 mm;工況二:柱截面為1 600 mm。如圖16所示,工況一(小截面柱)的負彎矩屈服線沿梁邊,正彎矩屈服線通過柱且與梁成45°,均與圖15的屈服線一致。從圖17可以看出,工況二(大截面柱)的負彎矩屈服線近似為沿梁跨中分布并經過柱角的八邊形。正彎矩屈服線近似為經過梁跨中的十字形。大截面柱的樓板正負彎矩屈服線可近似為如圖18所示的模式。

板的極限分析有上限法和下限法[1],上限法較常用。上限法求出板的極限荷載低于真實解的前提是假定的破壞機構是正確的。顯然柱截面較大時,傳統假定的正彎矩屈服線不正確,通過其求得板所能承受的極限荷載可能高于真實值。因此,對于大截面柱框架結構樓板,采用矩形板的極限分析,偏不安全。

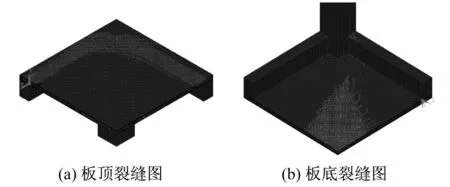
圖16 小截面柱板裂縫圖Fig.16 Slab crack distribution of slender column

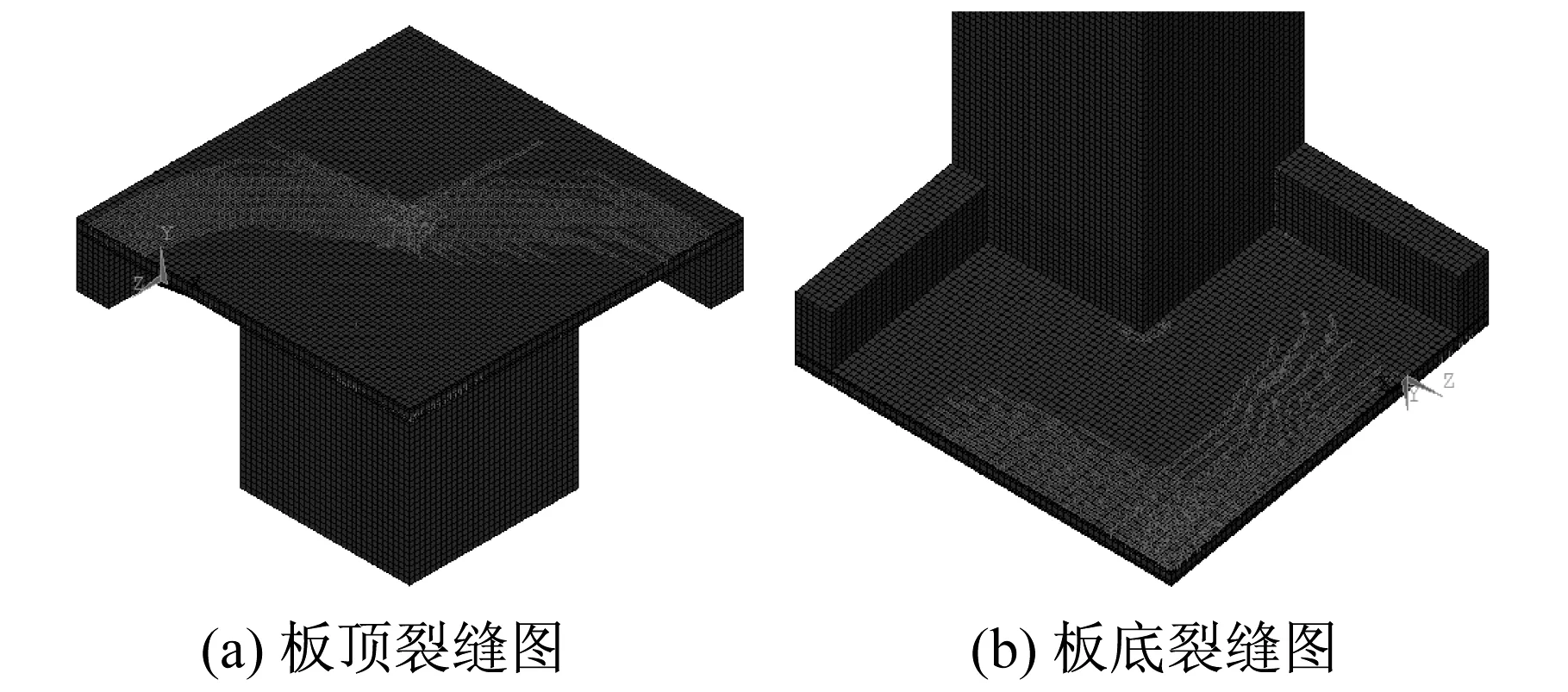
圖17 大截面柱板裂縫圖Fig.17 Slab crack distribution of fat column

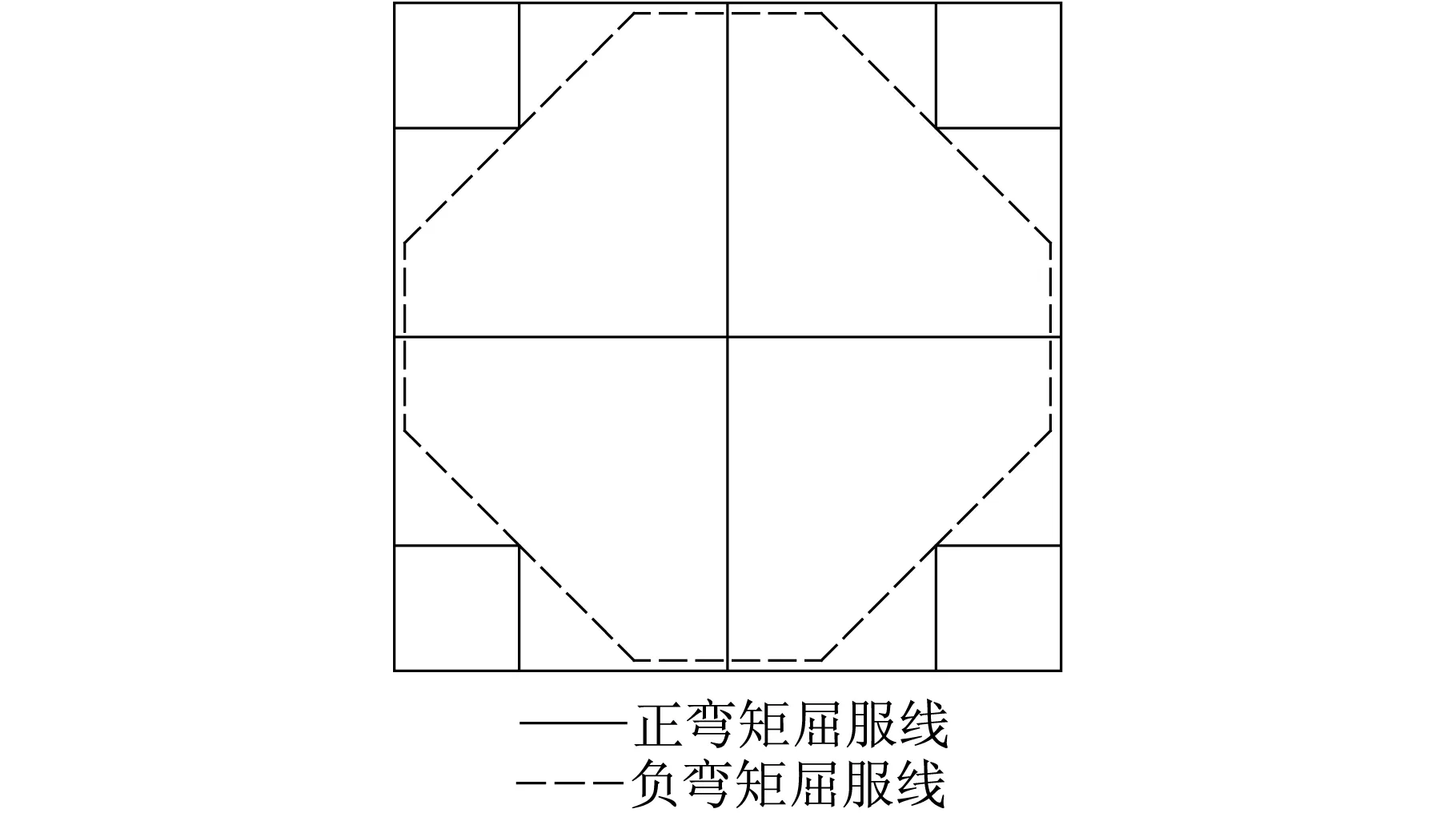
圖18 大截柱樓板屈服線示意圖 Fig.18 Slab yield line of fat column

2 大截面柱框架結構實際工程分析

本節通過ANSYS對某大截面柱框架結構實際工程中樓板開裂比較嚴重的一部分進行非線性有限元分析,對比有限元計算結果與實際工程樓板開裂情況,驗證ANSYS分析結論的有效性和準確性。

在車間的一角，有個碩大的池子，里面裝滿紅褐色的液體，聞那氣味估計是一種化工原料，木材加工廠老板收購來的一部分質地堅硬的木材，都被加工成木方，浸泡在里面。剛開始賈鵬飛不懂這是做什么的，后來聽工友介紹說浸泡的木材，經過高溫蒸干定型，再拿去打造高檔的紅木家具，由于材質細密，內外木質泛紅，與真的紅木就沒有什么差別了。想想商場幾萬元一張的餐桌，這“紅木家具”真是暴利。

2.1 模型概況

模型梁柱布置及部分尺寸如圖19所示,主梁截面為350 mm×700 mm,次梁截面為250 mm×500 mm,板厚120 mm,層高為5.7 m。構件材料強度和本構關系同算例1.1。板底雙向配筋均為6@160,板面配6@160的負彎矩鋼筋。鋼筋均為HRB335級鋼。ANSYS分析采用整體式模型,混凝土采用Solid65單元。

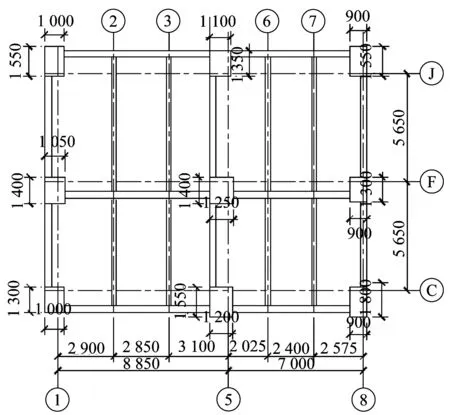
圖19 梁柱平面布置示意圖(單位:mm)Fig.19 Position of beam and column (Unit:mm)

2.2 板的裂縫及結論

ANSYS計算的板頂裂縫如圖20所示。實際工程中樓板開裂情況如圖21所示(為便于辨別,圖中裂縫均已描繪處理。對比圖20和圖21可知:①裂縫出現的位置基本位于柱子附近,與實際工程出現的裂縫情況類似;②靠近柱子的部分裂縫走向和角度與實際工程相同。上述分析表明:應用ANSYS進行鋼筋混凝土樓板分析是可行的。

圖21 實際工程板面裂縫Fig.21 Surface cracks on slabs

3 樓板構造措施探索

鑒于大截面柱產生裂縫的規律,本節研究其在豎向荷載作用下,不同構造配筋對板頂裂縫控制的影響,并提出有效可行的構造措施。

3.1 算例

本節采用ANSYS軟件進行非線性分析。模型具體尺寸:跨度(L)采用4 800 mm,層高為3 000 mm,梁截面為300 mm×500 mm,柱截面(C)為1 600 mm×1 600 mm,板厚為120 mm。混凝土采用Solid65單元,構件的混凝土強度等級均取C30,抗拉強度采用其標準值為2.01 MPa,泊松比為0.2,膨脹系數為1×10-5/℃。除自重外,考慮3 kN/m2的樓面活荷載,溫差取25°。板底雙向配筋均為10@150,板面配10@100的負彎矩鋼筋。梁受拉和受壓區均為6根22的鋼筋,箍筋為10@100,柱子配筋率為2%,鋼筋均為HRB400級鋼。

3.2 不同柱截面下板的裂縫分布

為對比柱截面變化對框架結構樓板裂縫控制的影響,本節介紹以下三種算例。

算例1:柱截面為600 mm,支座負彎矩鋼筋伸入板內1 300 mm,如圖22所示。

算例2:柱截面為1 000 mm,距柱邊1 000 mm范圍內的支座負彎矩鋼筋伸入板內2 000 mm,其余支座負彎矩鋼筋伸入板內1 300 mm,如圖23所示。

算例3:柱截面為1 600 mm,距柱邊1 000 mm范圍內的支座負彎矩鋼筋伸入板內2 600 mm,其余支座負彎矩鋼筋伸入板內1 300 mm,如圖24所示。

從圖22-圖24可以看出,柱截面為600 mm時板頂未見開裂現象;柱截面為1 000 mm時板頂在柱角處有裂縫;柱截面為1 600 mm時樓板開裂現象比較明顯,主要為與梁呈45°的板角裂縫及柱、板結合部裂縫。

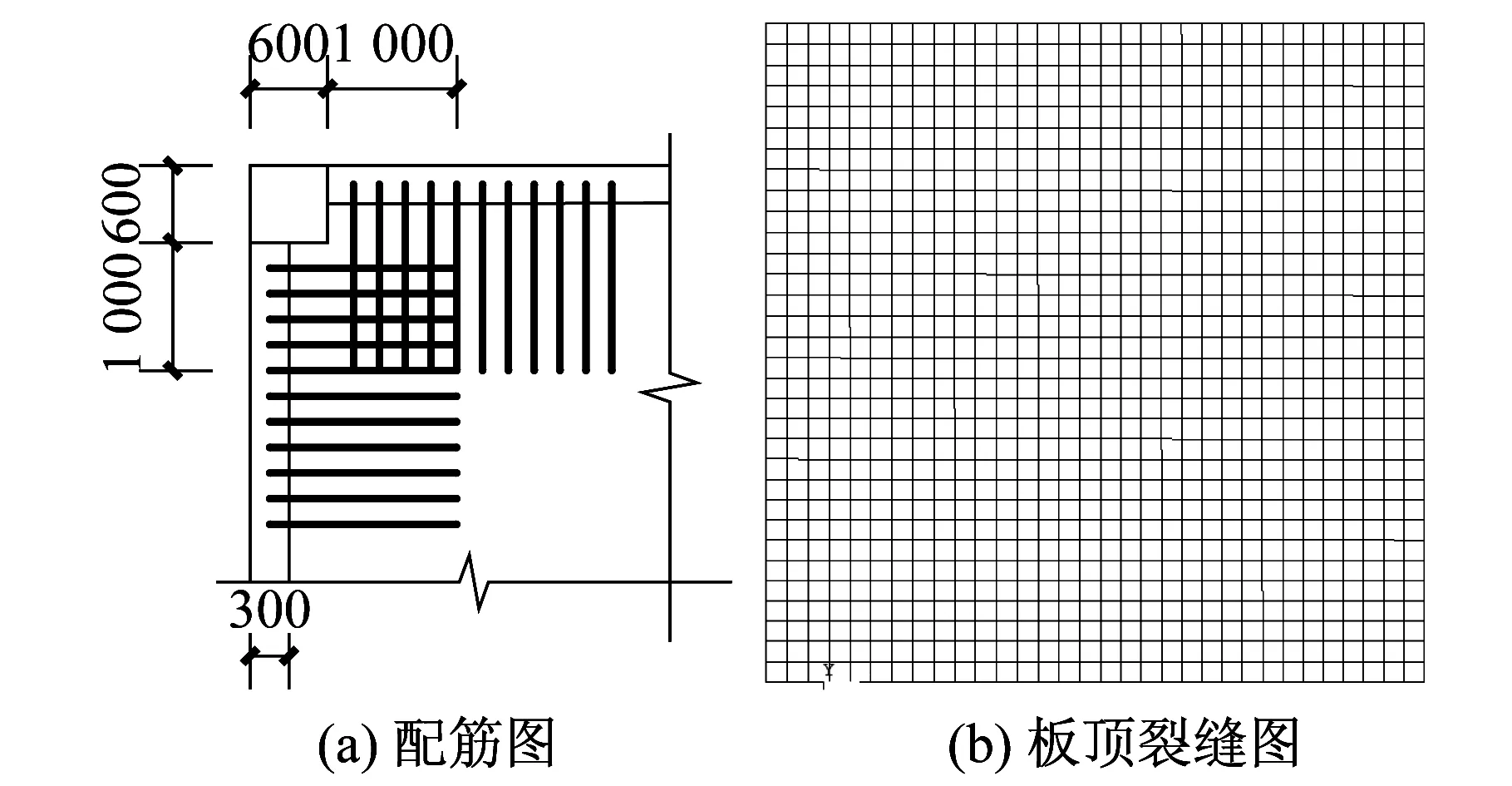
圖22 算例分析1 (單位:mm)Fig.22 The first case study (Unit:mm)

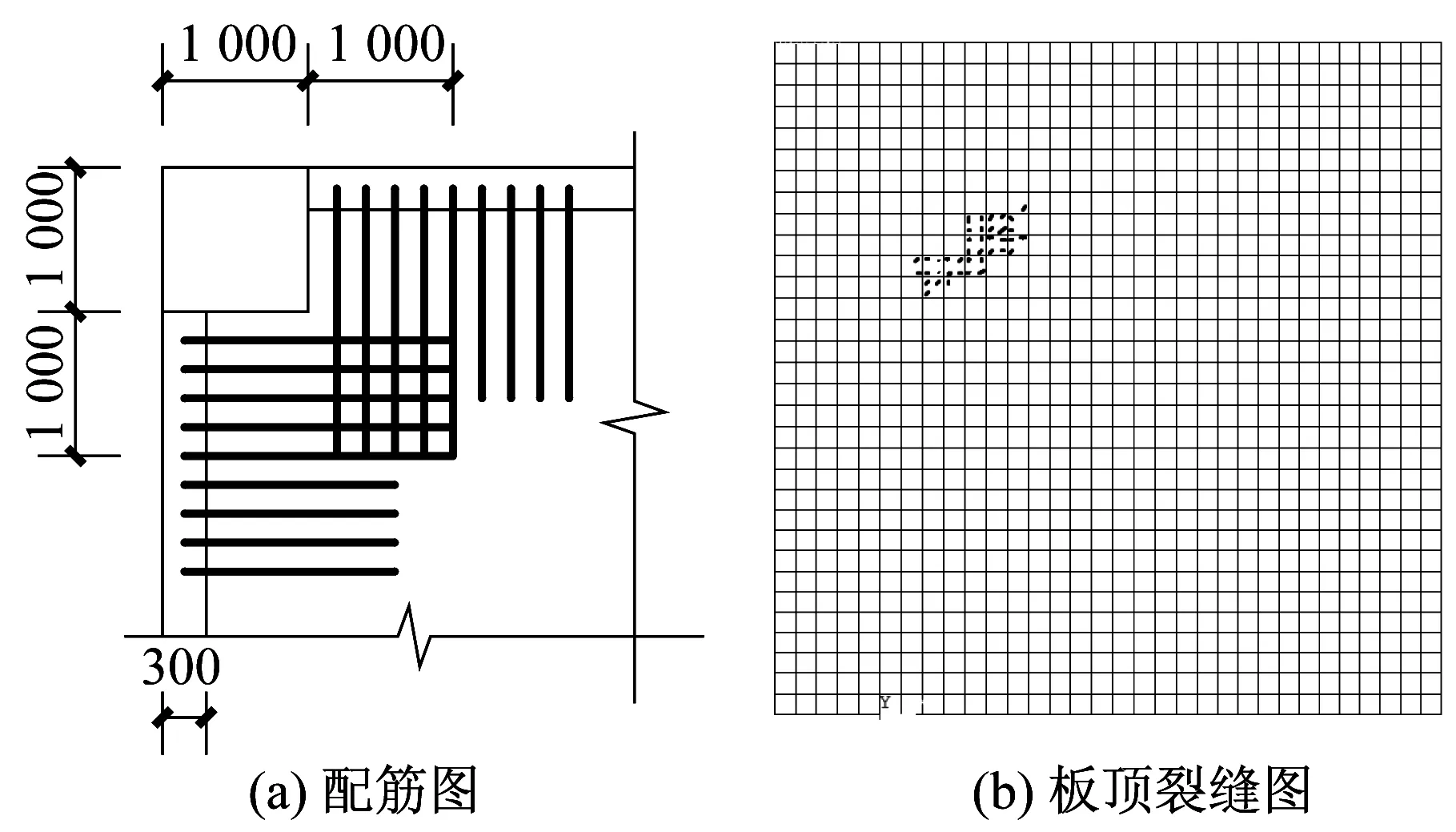
圖23 算例分析2 (單位:mm)Fig.23 The second case study (Unit:mm)

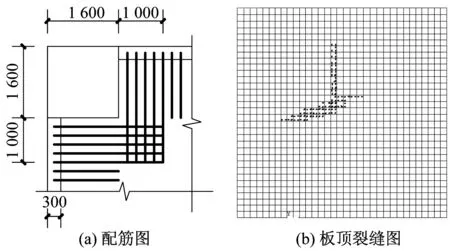
圖24 算例分析3 (單位:mm)Fig.24 The third case study (Unit:mm)

從以上三個算例可以看出:柱截面越小,板頂的裂縫現象越少;柱截面越大,裂縫現象越明顯。對于算例三的大截面柱的樓板裂縫現象嚴重,現對其進行局部加密配筋,建立算例4,配筋如圖25所示。

圖25 算例分析4 (單位:mm)Fig.25 The forth case study (Unit:mm)

算例4中的構造措施對大截面柱柱角處裂縫控制不理想,如果繼續增配鋼筋,會使柱角處鋼筋過去不易綁扎。因此,僅考慮加強配筋無法滿足大截面柱裂縫控制要求。參考無梁樓蓋板柱節點的結構形式,在算例3的基礎上增加托板,如圖26算例5所示。

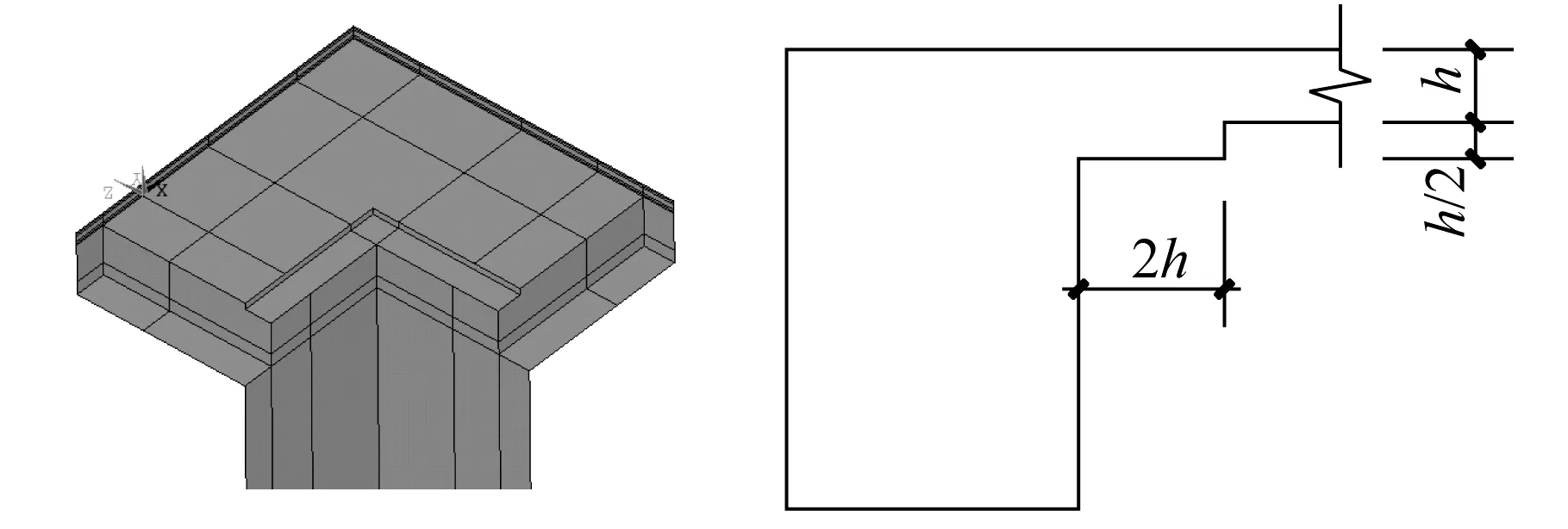
圖26 算例分析5的模型及尺寸示意圖Fig.26 Model and dimension of the fifth case study

圖27為算例5板頂裂縫圖。從兩圖中可以看出,加上托板后,樓板柱角處未見有開裂現象。因此,加托板等構造措施可以有效地解決柱角處裂縫問題。

圖27 算例分析5的板面裂縫Fig.27 Slab crack of the fifth case study

5 結 論

(1) 豎向荷載作用下,板柱角處板頂主拉應力隨柱截面增加而增加,且增幅顯著;梁跨中板頂主拉應力隨柱截面的增加而減小;隨柱截面增加,板頂最大主拉應力從梁跨中處向柱角處轉移。

(2) 豎向荷載作用下的樓板板帶彎矩:隨柱截面增大柱角處樓板負彎矩先增大后減小,沿樓板對角線方向板帶的反彎點逐漸向板中心偏移,板跨中板帶反彎點位置基本不變;梁跨中處樓板負彎矩隨柱截面增大而減小;柱截面變化對樓板零彎矩線有顯著影響,按矩形板布置負彎矩鋼筋無法覆蓋大截面柱框架結構樓板的負彎矩區域。

(3) 豎向荷載作用下的樓板屈服線:柱截面變化對樓板彎矩屈服線影響顯著;柱截面較小時,樓板負彎矩屈服線為沿著梁邊分布的四邊形,正彎矩屈服線近似為沿板對角線成X形;但當柱截面較大時,樓板負彎矩屈服線近似為沿梁跨中分布并經過柱角的八邊形,正彎矩屈服線近似為經過梁跨中的十字形;對于大截面柱框架結構樓板,按照矩形板進行塑性計算,因屈服線假定有誤而偏不安全。

(4) 樓板裂縫控制:大截面柱框架結構樓板裂縫主要有板、柱結合部裂縫和板角斜裂縫;采用不同的柱角處構造措施其裂縫控制效果不同;相比而言,在柱角處配置正交鋼筋并加上托板可有效地控制大截面柱框架結構樓板裂縫。

[1] Park R,Gamble W L.Reinforced Concrete slabs,Second Version[M].USA:Wiley,1999.

[2] 童申家,童岳生,栗海濤,等.復雜邊界支撐的鋼筋混凝土矩形板的極限設計[J].建筑結構,2004,34(6):25-27.

Tong Shenjia,Tong Yuesheng,Li Haitao,et al.Limit design of reinforced concrete rectangular slabs with complex boundary[J].Journal of Building Structures,2004,34(6):25-27.(in Chinese)

[3] Bungale S.Taranath.Reinforced concrete design of Tall Buildings[M].Talyor & Francis Group,2010.

[4] 劉文珽,黃承逵.配置抗沖切鋼筋的混凝土異形柱-板柱連接試驗研究[J].土木工程學報,2005,38(3):23-29.

Liu Wenting,Huang Chengkui.Experimental investigation on the behavior of slab-nonrectanglular column connections with shear reinforcement[J].China Civil Engineering Journal,2005,38(3):23-29.

[5] 李占鴻.虹橋機場周邊某既有住宅陽臺改造加固的ANSYS 有限元分析及荷載試驗驗證[J].結構工程師,2014,30(3):175-180.

Li Zhanhong.Analysis by ANSYS and load test verification of the strengthened balcony of existing residential around hongqiao airport[J].Structural Engineers,2014,30(3):175-180.(in Chinese).

[6] Burgess I.Yield-line plasticity and tensile membrane action in lightly-reinforced rectangular concrete slabs[J].Engineering Structures,2017,138:195-214.