潤滑狀態下導軌結合面法向動態接觸剛度實驗研究

任 鵬 王立華 汪純鋒

昆明理工大學機電工程學院，昆明,650500

0 引言

機床中各結合面的動態性能對機床整體的動力學特性有著重要的影響。滑動導軌作為功能性部件在機床上應用廣泛。導軌結合面的接觸形式在微觀角度表現為線接觸或點接觸，故結合面的剛度在很大程度上影響機床的加工精度[1]。為了使滑動導軌結合面的動態特性參數更加準確，一些專家進行了相關研究。田紅亮等[2]根據赫茲接觸基礎理論，進行了兩圓柱微凸體間的法向接觸剛度推導。莊艷等[3]在彈塑性理論的基礎上，推導出不同的變形類型下，單對微凸體在側接觸情況下的法向接觸剛度，并通過實驗驗證了該推導方法的可靠性。STARZYNSKI等[4]通過超聲波法測量了三種不同接觸面下結合面的接觸剛度和剪切剛度，發現接觸剛度是非線性的。QIN等[5]研究了潤滑狀態下線接觸模型，在彈流潤滑模型基礎上得到接觸剛度模型，在較大載荷、相對低速、小曲率微凸體的等效半徑情況下，該模型計算結果與赫茲接觸剛度很相近。苗青[6]總結出不同因素對靜剛度的影響規律。胡殿印等[7]提出了一種基于模態實驗的結合面接觸剛度計算方法，并驗證了計算方法的準確性。BRIZMERA等[8]等應用了一種利用有限元法求解阻尼器接觸剛度的方法，該方法的研究對象為一個圓弧表面和一個平面之間的結合面接觸，并不符合真實的微觀粗糙表面的結合面接觸。BERTHOUD等[9]在實驗的基礎上分析了結合面正壓力和材料屬性對結合面接觸剛度的影響。劉意等[10]在前人實驗的基礎上創立了一種可以改進實驗的方法，使實驗誤差有效減小。唐強等[11]提出了一種三維真實的粗糙結合面接觸剛度研究方法，利用奧林巴斯LEXT OLS4000激光共焦顯微鏡獲取了粗糙結合面的真實微觀形貌，利用軟件處理后建立三維模型并導入ANSYS軟件進行計算。

綜上所述，目前的導軌接合面接觸特性研究多將構件接觸表面假設為各向同性的半球型微凸體模型，對圓柱微凸體接觸的研究較少。

本文搭建了動態信號測試系統實驗平臺，通過測試結合面的動態特性參數，得到了結合面動態固有頻率從而得到結合面的法向動態剛度，并探究了載荷、速度、有無潤滑對結合面動態剛度的影響規律。

1 滑動導軌結合面動態特性建模

根據機床的布局，滑動導軌安裝在地面，工作臺等運動部件安裝在滑塊上，而滑塊和導軌中間通過結合面連接，它們之間多為線接觸或點接觸。導軌與地面、工作臺與滑塊之間多為螺栓連接,剛度遠大于結合面的接觸剛度，因此,增大結合面接觸剛度就可以有效改善機床整體剛度。考慮潤滑狀態后，導軌結合面潤滑剛度模型如圖1所示。圖1中，Cin是入口區阻尼，h是油膜厚度，F是載荷，u是相對滑動速度，Kin是入口區剛度，Koil是油膜剛度，Kn是單個微凸體剛度，δ是變形量，r是接觸區半徑。考慮油膜潤滑的情況，整個接觸區域可分為三部分：潤滑油入口區、赫茲接觸區、潤滑油出口區。

圖1 結合面微觀彈流潤滑接觸模型Fig.1 Microscopic binding surface model in contact EHL

如圖1所示，結合面接觸的彈流潤滑接觸模型可等效為入口油膜剛度、接觸區油膜剛度和接觸區法向剛度組成的串并聯模型。由串并聯結構關系可知，導軌結合面的綜合法向剛度[12]

(1)

對于線接觸彈性流體動力潤滑問題，DOWSON等[13]利用數值模擬和實驗測量的方法得到了大量數據，擬合出了計算最小油膜厚度與中心油膜厚度的經驗公式。Dowson-Hamrock量綱一最小油膜厚度的經驗公式為[13]

(2)

量綱一中心油膜厚度經驗公式為

(3)

u*=η0u/(E*r)G*=αlE*
W*=F/(E*r)

式中，上標“*”表示量綱一；u*為速度參數；G*為材料參數；αl為黏壓指數，一般取αl=2.210-8Pa-1；W*為載荷參數;ω為接觸區內外彈性變形；E*為量鋼一彈性模量。

根據Hertz接觸理論得單個微凸體的法向接觸剛度：

(4)

式中，E為彈性模量；A為接觸面積。

在式(3)中，對中心油膜厚度求偏導即可得到載荷與中心油膜厚度hc的關系[14]，即

(5)

由此可知,油膜剛度與接觸表面速度、載荷和潤滑情況有關。根據式(5)可知，當載荷增大時油膜剛度應增大；滑動速度增大時油膜剛度應減小。

2 潤滑導軌結合面實驗臺設計

以機床y向滑動導軌為模型，搭建圖2所示的測試系統，用于識別滑動狀態下結合面動態特性參數，測出不同結合面正壓力(下稱“面壓”)或不同滑動速度下結合面剛度參數。其中，滑塊材料為HT200，導軌材料為45鋼，潤滑油為加德士導軌油ISO68，接觸面積A=0.031 2m2，試驗動滑塊質量m=25.98 kg，表面粗糙度數據如表1所示，測試3次，取平均值。

圖2 滑動導軌結合面動態特性測試系統Fig.2 Test system for characteristic parametersof sliding trail interface

Ra1Ra2Ra3Ra平均值導軌表面0.8140.7830.8260.808滑塊表面0.7770.7940.8420.804

滑動導軌結合面動態特性參數測試裝置示意圖見圖3。在模態分析時設置好各項參數，由信號發生器發出掃頻信號，由數據采集器采集數據并輸入計算機，通過變換得各點頻響函數，由峰值共振法得到滑動導軌結合面的單位面積動剛度。

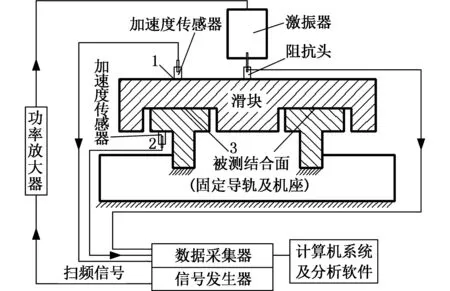
圖3 測試裝置示意圖Fig.3 Schematic diagram of the testing device

如圖3所示，測量微凸體的變形與固定導軌變形(固定導軌的位移為基礎位移)，求兩者變形之差即為結合面3處的位移。由于無法直接測得結合面的變形大小，且滑塊與固定導軌剛度遠大于結合面剛度，故用滑塊1處的數據表示滑塊3處的數據，用固定導軌2處的數據表示固定導軌3處的數據。為盡可能減小誤差，激振點應選質心位置，激振系統應與滑塊同步運動以保持激振同步。

導軌結合面的法向單位面積動剛度Ks識別步驟如下：①測得滑塊及固定導軌的頻響函數HX(ω)、HY(ω)；②利用峰值共振法得到滑動導軌系統整體的固有頻率fn，然后通過公式

K=m(2πfn)2

(6)

計算系統的等效剛度K；③根據結合面面積A計算出結合面單位面積法向動剛度Ks。

3 結合面動剛度的實驗研究

電機低速轉動時易產生爬行現象，轉速較高時則不會發生爬行現象，且滑塊滑動速度是影響機床導軌穩定性的重要因素，因此滑動速度與結合面的動態特性有很大關系。

機床在加工工件時，切削力的產生會引起滑動導軌結合面的載荷變化，因此分析面壓對滑動結合面動態特性的影響具有重要意義。

在速度和面壓一定時，比較有無潤滑情況下結合面剛度的大小，查看有無潤滑對結合面剛度的影響。各影響因素的取值見表2。

3.1 無潤滑狀態不同因素對動剛度的影響

3.1.1滑塊速度對剛度的影響

在5種不同滑塊速度下進行測試并與靜態數據進行對比，令滑塊的相對運動速度v為0，20，25，30，35，40 mm/s。繪制各點的頻響函數曲線，并進行程序運算處理，最后計算得到各實驗條件下結合面單位面積剛度。

表2 滑動結合面動態特性的影響因素

以滑塊運動速度v=30 mm/s，面壓p0=0時的實驗為例，測試得到加速度頻響函數曲線如圖4所示。

圖4 加速度頻響函數曲線Fig.4 Acceleration frequency-response function curve

根據圖4，當頻響函數峰值對應的相位是90°或-90°時，該峰值對應的頻率即為該系統的固有頻率，故系統的固有頻率fn為406.3 Hz，由式(6)計算得該滑動導軌系統的法向等效剛度K為1.693×108N/m，由此得到滑動導軌結合面的單位面積法向動剛度Ks為5.427 GN/m3。

同理，實驗得到不同速度下的單位面積法向動剛度，如圖5所示。

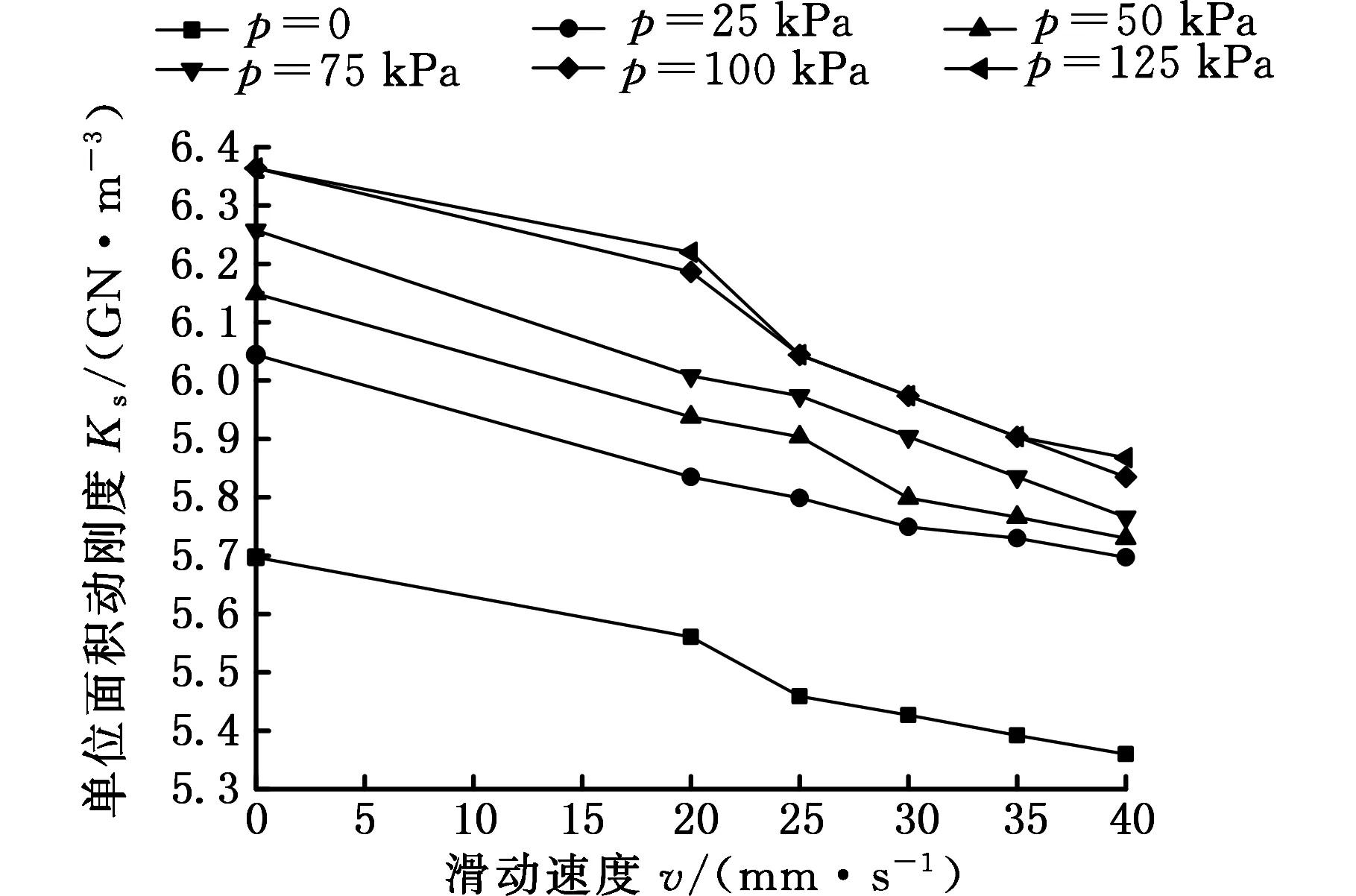
圖5 不同速度下鋼-鑄鐵導軌單位面積動剛度變化曲線Fig.5 Curves of dynamic stiffness of steel-cast iron guide under different velocities

相比靜止情況，滑動導軌結合面運動狀態下的法向剛度減小，這是因為運動過程中接觸對不斷地改變，且接觸對減少的速度遠大于新接觸對產生的速度，而速度越大，接觸對改變的頻率越高，導致結合面實際接觸面積遠小于靜止狀態下的實際接觸面積，故其單位面積動剛度小于靜止狀態下的單位面積動剛度。速度的加快會使實際接觸面積減小，所以滑動導軌結合面的等效剛度也變小。但在結合面所受面壓較大時，實際接觸面積變化較小，剛度變化趨勢略微平緩。

3.1.2面壓對剛度的影響

實驗通過螺栓在法向對結合面施加不同預緊力矩進行加載。面壓分別為0，25，50，75，100，125 kPa。通過兩個螺栓加載，如圖6所示，沿滑塊運動方向分布于滑塊中心，距前后各49 mm。

圖6 加載螺栓分布示意圖Fig.6 Loading bolt distribution schematic diagram

測得加載用螺栓直徑為12 mm，計算得各面壓對應的螺栓加載力矩Tn分別為1.9，3.7，5.6，7.5，9.4 N·m。測得不同情況下的頻響函數曲線，通過等效單自由度程序處理，計算得各面壓下結合面單位面積法向動剛度,如圖7所示。

導軌結合面的法向動剛度隨著面壓的增大而增大，因此適當增加面壓會增大導軌結合面的法向動剛度。當面壓增加到100 kPa之后，法向靜剛度變化趨于平緩。

3.2 潤滑狀態下不同因素對動剛度的影響

3.2.1滑動速度對剛度的影響

在導軌結合面上均勻涂上加德士導軌油ISO68，驅動電機令滑塊以0，20，25，30，35，40 mm/s的運動速度滑動,繪制出各速度下各點的頻響函數曲線，最后計算得到各實驗條件下結合面單位面積動剛度，如圖8所示。

圖8 速度對結合面動剛度的影響Fig.8 The influence of velocity on the dynamic stiffness

在靜止狀態下由于潤滑油膜填充了微凸體間的間隙，故在油膜剛度的作用下，不同載荷對法向剛度影響較小，輕載低速狀態下剛度變化較大，法向剛度隨著滑動速度的增大而降低。

3.2.2面壓對剛度的影響

在潤滑條件下，對結合面進行5組相同的加壓實驗，加載面壓分別為0，50，100，150，200 kPa。測得結合面動剛度隨面壓的變化曲線(圖9)。由圖9可知，面壓的增大一般會導致單位面積動剛度的增大，因為面壓增大會使接觸對的接觸面積增大，未接觸的微凸體也會產生新的接觸對，總體實際接觸面積增大，故單位面積動剛度有所增大。當面壓增大到一定值時，接觸對的變形能力降低，加壓對接觸面積的影響不大，故此時面壓對結合面單位面積動剛度的影響較小，單位面積動剛度變化趨于平緩。

圖9 面壓對結合面動剛度的影響Fig.9 The influence of surface pressure on dynamic stiffness

3.3 有無潤滑狀態下結合面剛度比較

潤滑和干摩擦狀態下結合面動靜剛度如圖10所示。由圖10可知，相同狀態下，添加潤滑介質可以增大結合面動剛度5%左右。當速度由0增加到40 mm/s時，干摩擦狀態下結合面的動剛度減小約7 GN/m3，而潤滑狀態下的結合面動剛度減小5 GN/m3，有效說明了潤滑介質可以改善結合面剛度。

(a)p=0 (b)p=25 kPa

(c)p=50 kPa (d)p=75 kPa

(e)p=100 kPa (f)p=125 kPa圖10 潤滑和干摩擦狀態下結合面動靜剛度對比Fig.10 Comparison of static and dynamic stiffness with lubrication and dry friction

根據潤滑機理，結合面滑動會產生兩種不同的潤滑油膜：一種為物理油膜，即潤滑油在范德華力的作用下使油膜中的極性分子定向排列成一層分子膜吸附到導軌表面；另一種是化學吸附膜，即主要依靠潤滑油極性分子中的有價電子與導軌表面的金屬電子產生的化學結合力。微觀上，結合面表面凹凸不平存在很多溝壑，溝壑中會殘留部分潤滑油，當滑動速度大到一定數值時，會發生微觀層面的流體動壓潤滑現象。而微觀層面的動壓潤滑形成的油膜使得兩接觸表面并未直接接觸，中間保持油膜層，提高了潤滑油膜的承載能力，從而有效增大了結合面的動態剛度。

由以上實驗結果可知：當載荷增大時，油膜剛度增大；滑動速度增大時，油膜剛度減小。與前文中式(5)所示規律一致。

滑動速度、面壓、有無潤滑對結合面剛度的影響如圖11所示。

圖11 影響因素分析三維圖Fig.11 Three dimensional diagram of influencefactors analysis

4 結論

(1) 滑動速度的增大會使結合面動剛度減小，當結合面面壓較大或存在潤滑時，速度對動剛度的影響較小，反之,面壓較大且干摩擦狀態下速度對動剛度影響較大。

(2) 面壓的增大可以提高結合面動剛度，但增大到一定值時動剛度變化趨于平緩。

(3) 潤滑油膜可以有效改善結合面動剛度。本文通過實驗說明，在載荷較小時油膜對結合面整體動剛度影響較大，不可忽略。

參考文獻：

[1] 巫修海,朱壯瑞.基于模態試驗的機床導軌滑塊結合面的參數識別研究[J]. 機械制造，2007,45(8):64-66.

WU Xiuhai, ZHU Zhuangrui. Parameter Identification of Slide Block Joint Surface of Machine Tool Guideway Based on Modal Test [J]. Machinery Manufacturing,2007,45(8):64-66.

[2] 田紅亮,朱大林,秦紅玲.固定接觸界面法向靜彈性剛度[J].應用力學學報, 2011,28(3):318-322.

TIAN Hongliang, ZHU Dalin, QIN Hongling. Normal Static Elastic Stiffness of Fixed Contact Interface[J]. Journal of Applied Mechanics, 2011,28(3):318-322.

[3] 莊艷，李寶童，洪軍，等.一種結合面法向接觸剛度計算模型的構建[J].上海交通大學學報,2013,47(2):180-186.

ZHUANG Yan, LI Baotong, HONG Jun,et al. Construction of a Calculation Model for Normal Contact Stiffness of Joint Surface[J]. Journal of Shanghai Jiao Tong University,2013,47(2):180-186.

[4] STARZYNSKI G, BUCZKOWSKI R. Ultrasonic Measurements of Contact Stiffness between Rough Surfaces[J]. Journal of Tribology,2014,136(3):034503.

在進行課本劇內容的準備過程中，我們一定要按照尊重原文內容的原則進行創作，然后結合學生的認知和心理特點改編課文，讓學生經過對課本劇的學習能夠快速理解文章，發揮課本劇教學優勢，增加對文章的掌握程度。

[5] QIN W, CHAO J, DUAN L. Study on Stiffness of Elastohydrodynamic Line Contact[J]. Mechanism & Machine Theory,2015,86(86):36-47.

[6] 苗青.數控機床導軌結合面的接觸剛度分析[D].洛陽：河南科技大學, 2014.

MIAO Qing. Contact Stiffness Analysis of the Joint Surface of Numerical Control Machine Tool [D]. Luoyang：Henan University of Science and Technology, 2014.

[7] 胡殿印,司武林,魏佳明.一種基于模態實驗的接觸剛度計算方法[J].航空動力學報, 2015, 30 (1):76-81.

HU Dianyin, SI Wulin, WEI Jiaming. A Method for Calculating Contact Stiffness Based on Modal Experiments[J].Journal of Aeronautical Power, 2015, 30 (1):76-81.

[8] BRIZMERA V, KLIGERMANA Y, ERSIONA L. Elastic-plasric Spherical Contact under Combined Normal and Tangential Loading in Full Stick[J]. Tribology Letter, 2007, 25(1):61-70.

[9] BERTHOUD P, BAUMBERGER T. Shear Stiffness of a Solid-solid Multi-contact Interface[J]. Mathematical Physical and Engineering Science,1998,454:1615-1634.

[10] 劉意,劉恒,易均.切向接觸剛度測量方法的理論改進[J].西安交通大學學報, 2012,46(1):66-69.

LIU Yi, LIU Heng, YI Jun. Theoretical Improvement of Measurement Method for Tangential Contact Stiffness [J]. Journal of Xi'an Jiaotong University, 2012,46(1):66-69.

[11] 唐強,王崴,龔水清.三維真實粗糙接合面法相接觸剛度研究[J].機械設計, 2012,29(11):8-11.

TANG Qiang, WANG Wei, GONG Shuiqing. Study on Phase Contact Stiffness of Three Dimensional Real Rough Joint Method [J]. Machine Design, 2012,29(11):8-11.

[12] 李昌,孫志禮.基于彈流潤滑理論的深溝球軸承動態虛擬仿真[J].航空動力學學報,2009,24(4):951-956.

LI Chang, SUN Zhili. Dynamic Virtual Simulation of Deep Groove Ball Bearing Based on Elastohydrodynamic Lubrication Theory [J]. Journal of Aerodynamics,2009,24(4):951-956.

[13] DOWSON D, HAMROCK B J. Numerical Evaluation of the Surface Deformation of Elastic Solids Subjected to a Hertzian Contact Stress[J]. Tribology Transactions, 1976, 19(4):279-286.

[14] 曹樹謙,張文德,蕭龍翔.振動結構模態分析:理論、實驗與應用[M].天津:天津大學出版社, 2014.

CAO Shuqian, ZHANG Wende, XIAO Longxiang. Modal Analysis of Vibration Structures: Theory, Experiment and Application[M]. Tianjin: Tianjin University Press,2014.