常用坐標系之間的轉換方法研究

劉可可，陳亮，馬麗亞

（中國船舶重工集團公司第七一三研究所，河南 鄭州 450015）

在測量和GPS應用中，坐標系的概念及相互之間的轉換是必不可少的，任何測量和繪圖工作都要在一定的參考系中進行。在導航系統中常用到的坐標系包括地理坐標系、地心地固坐標系和導航坐標系。

1 坐標系概述

（1）地理坐標系（t系，hlL,,）。地理坐標系OX tttZY，其原點位于運載體所在的點，tX軸沿當地緯線指東， Yt軸沿當地子午線指北， Zt軸沿當地地理垂線指下并與 Xt， Yt軸構成右手直角坐標系。其中 Xt軸與 Yt軸構成的平面即為當地水平面； Yt軸與 Zt軸構成的平面即為當地子午面。

（2）地球坐標系（e系， X ,Y ,Z）。地球坐標系OXeYeZe，其原點取在地心，Ze軸沿極軸(地軸)方向，Xe軸在赤道平面與本初子午面的交線上， Ye軸也在赤道平面上并與 Xe， Ze軸構成右手直角坐標系。地球坐標系與地球固連，隨地球一起轉動，因此又稱為地心固聯（ECEF，Earth-Centered，Earth-Fixed）坐標系。地球繞極軸作自轉運動，并且沿橢圓軌道繞太陽作公轉運動。地球表面任意一點的位置均可用經度和緯度來確定。

（3）導航坐標系（n系， N ,E ,D）。導航坐標系是一種當地地理坐標系。它是指在導航時，根據導航系統工作所需要而選取的用來作為導航基準的坐標系。原點O在載體的重心，Oyn指向北，Oxn指向東，Ozn沿垂直方向指向地。故此坐標系亦稱為北東地（NED）坐標系。

2 坐標系之間的轉換

一個坐標系到另一個坐標系之間的轉換，可以通過繞不同的坐標軸3次旋轉來實現。假設直角坐標系OXYZ，繞X軸旋轉一個角度α，坐標旋轉矩陣用Cx(α)表示，則：

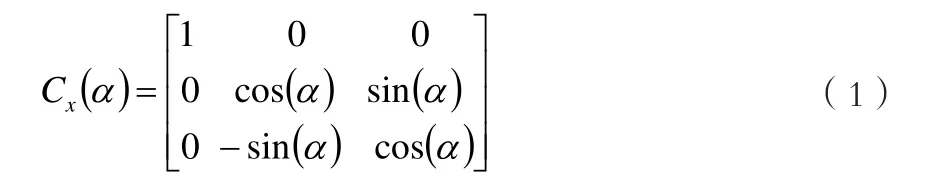
繞Y軸旋轉一個角度β，坐標旋轉矩陣用 Cy(β)表示，則：

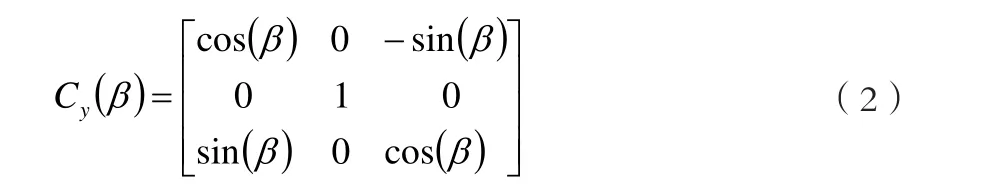
繞Z軸旋轉一個角度γ，坐標旋轉矩陣用 Cz(γ)表示，則：

由上可知，坐標系之間的轉換是通過 Cx(α)、Cy(β)、 Cz(γ)這3個獨立變換的乘積得到的。

（1）地理坐標系與地球坐標系之間的轉換。已知目標在地理坐標系下的緯度、經度、高度(L ,l ,h)，計算在ECEF下的坐標(X ,Y ,Z)，公式如下：

其中，l的取值是相對于格林威治子午線的。

為了避免L的迭代，也可以采用以下公式計算L：

常采用以下公式計算h：

（2）地球坐標系（e系）與導航坐標系（n系）之間的轉換。已知原點坐標記為緯度 L0、經度 l0和橢球高h0，根據公式（4）可以計算出地球的原點坐標 X0、 Y0、Z0。導航坐標(N ,E ,D)可以用下式計算得到：

從導航坐標到地球坐標的逆轉換公式如下：

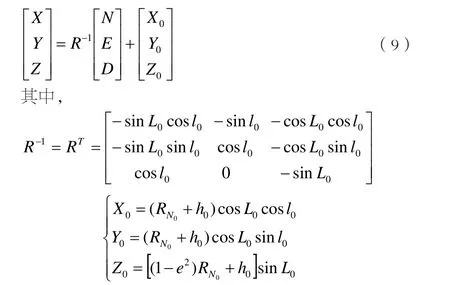
RN0為緯度 L0處的卯酉圈半徑，

（3）地理坐標系(t系)與導航坐標系(n系)之間的轉換。通過前面的介紹，導航坐標系可以由地理坐標系推算得到。也可以進行直接轉換，其轉換公式如下：

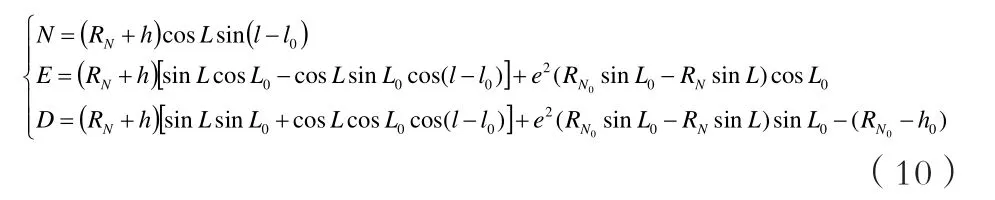
將導航坐標系坐標 ),,( DEN 逆變換為經度、緯度和高度 )h,,( lL ，具體過程如下所述。

首先將導航坐標系坐標轉換為地理坐標系坐標，即計算 ),,( ZYX ，公式如下：

然后將地球坐標系坐標轉換為地理坐標，公式如公式（5）所示，此處不再贅述。

3 仿真結果及分析

設置初始緯度L：36．41°，經度l：94．9°，高度h：4500米。下面以地球坐標系轉換為地理坐標系為例，其仿真結果如下圖1、2。

圖1 地球坐標系下的曲線

從圖2的曲線趨勢可以看出，初始高度為4500米，升高到約10000米時落下，又到約同一個高度，并且緯度、經度變化不大，所以得出圖1地球坐標系轉換為圖2地理坐標系，轉換過程是對的。由以上兩個圖可以看出上述轉換過程是正確的。

本文對于常用坐標系之間的轉換方法研究，不僅對衛星、導彈等高精度定位提供重要技術，并且能夠為組合導航系統數據進行密切銜接，實現數據融合等奠定基礎。

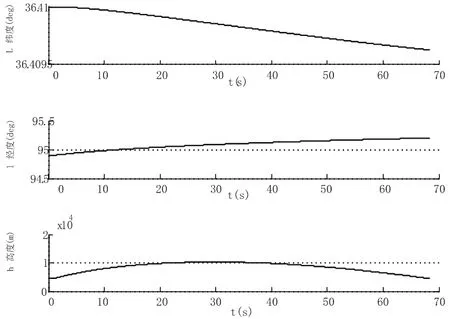
圖2 地理坐標系下的曲線

參考文獻:

[1]魏子卿．2000中國大地坐標系及其與WGS84的比較[J]．大地測量與地球動力學，2008,28(5):1-4．

[2]MORITZ H．The Geodetic Reference System 1980[J]．Journal of Geodesy，2000,(74):128-133．

[3]胡銳．慣性輔助GPS深組合導航系統研究與實現[D]．南京理工大學,2010．

[4]胡瑞,薛曉中,孫瑞勝等．制導炸彈中坐標系轉換的誤差分析及修正[J]．彈道學報，2008,20(4):36-40．

[5]王解先,王軍,陸彩萍．WGS-84與北京54坐標轉換的問題[J]．大地測量與地球動力學，2003,20(3):70-73．