已加工表面熱源模型研究及磨削溫度場數(shù)值模擬

王德祥, 孫樹峰, 顏丙亮, 劉新福, 江京亮

(1.青島理工大學(xué)機(jī)械工程學(xué)院, 266520, 山東青島; 2.山推道路機(jī)械有限公司研究院, 272103, 山東濟(jì)寧)

磨削加工需要極高的能量比,絕大部分能量都在磨削區(qū)轉(zhuǎn)化為熱量[1]。磨削加工時傳入工件的熱量會在工件表層產(chǎn)生高溫以及極大的溫度梯度,導(dǎo)致工件產(chǎn)生熱損傷。磨削溫度場是研究磨削熱損傷的重要依據(jù)。

隨著計算機(jī)技術(shù)的快速發(fā)展,數(shù)值模擬技術(shù)成為研究磨削溫度場的重要方法。利用計算機(jī)進(jìn)行磨削溫度場的數(shù)值模擬,需要建立磨削溫度場的數(shù)值仿真模型。磨削溫度場的數(shù)值仿真模型可以分為淺磨模型和深磨模型[2],如圖1所示。淺磨模型不需要建立砂輪和工件接觸表面與工件已加工表面之間楔形區(qū)域的幾何模型,直接將熱源施加到已加工表面上;深磨模型需要建立楔形區(qū)域的幾何模型,并且需要劃分極為精細(xì)的網(wǎng)格,而楔形區(qū)域內(nèi)的網(wǎng)格一般具有較大的長寬比,容易導(dǎo)致計算結(jié)果不準(zhǔn)確[2]。因此,淺磨模型更加方便,常用于磨削溫度場的數(shù)值模擬。已加工表面熱源的分布形狀是進(jìn)入工件已加工表面的熱流密度分布,是利用淺磨模型研究磨削溫度場的重要基礎(chǔ)。目前,在利用淺磨模型進(jìn)行磨削溫度場的數(shù)值模擬時,一般把已加工表面熱源的分布形狀假設(shè)為直角三角形[3]、三角形[4]、拋物線[5]和橢圓[6]等形狀。但是,已加工表面熱源的分布形狀會隨著磨削工藝條件改變,上述假設(shè)都是基于特定的磨削工藝條件,不能普遍適用于所有的磨削工況。

(a)淺磨模型 (b)深磨模型圖1　磨削溫度場數(shù)值仿真模型

本文基于圓弧熱源模型、砂輪和工件接觸表面直角三角形熱源,計算了被磨工件的無量綱磨削溫度場,利用溫度匹配法進(jìn)行了反傳熱分析,建立了已加工表面熱源分布形狀的計算方法,采用有限元方法建立了磨削溫度場的數(shù)值仿真模型(淺磨模型),仿真計算了工件的磨削溫度場,并同實驗結(jié)果進(jìn)行了對比。

1　已加工表面熱源分布形狀計算方法

1.1　無量綱磨削溫度場計算

由于磨削區(qū)未變形切屑厚度沿砂輪和工件接觸表面趨于線性分布,并且磨削熱流密度與未變形切屑厚度幾乎成正比[7]。因此,砂輪和工件接觸表面熱源的分布不會隨著磨削工藝條件改變,接近于直角三角形分布,如圖2所示。

圖2　工件磨削區(qū)的熱源分布

在計算已加工表面熱源的分布形狀時,首先建立如圖2所示的直角坐標(biāo)系,然后基于圓弧熱源模型[8]、砂輪和工件接觸表面直角三角形熱源,計算被磨工件的無量綱磨削溫度場。無量綱磨削溫度場的表達(dá)式為

(1)

式中:vw是工件速度;α是工件材料的熱擴(kuò)散率,且α=k/(ρc),k、ρ和c分別是工件材料的熱導(dǎo)率、密度和比熱容;qw是傳入工件的平均熱流密度;T(x,z)是工件的磨削溫度場;lc是磨削接觸弧長,且lc=(aeds)1/2,ae是磨削深度,ds是砂輪直徑;λ是積分變量,表示接觸表面上任意一點;φi是接觸表面上任意一點處的接觸角,且λ=dsφi;K0是零階二類修正貝塞爾函數(shù);f(λ)是描述接觸表面熱源分布形狀的形函數(shù),對于直角三角形熱源,其形函數(shù)為

f(λ)=-2λ/lc

(2)

1.2　已加工表面熱源的形函數(shù)計算

(3)

式中:[xa,xb]是已加工表面熱源的分布區(qū)域;s(ω)是描述已加工表面熱源分布形狀的形函數(shù);ω是積分變量,表示已加工表面熱源分布區(qū)域內(nèi)的任意一點。

在計算已加工表面熱源的形函數(shù)時,首先將已加工表面熱源的分布區(qū)域等分為m個區(qū)間,然后利用溫度匹配法[10]進(jìn)行反傳熱分析,可得以下方程組

(4)

(5)

式中:ωi和ωi+1是第i個區(qū)間的積分下限和積分上限,表述為

(6)

最后,對式(4)進(jìn)行數(shù)值求解,即可得到描述已加工表面熱源分布形狀的形函數(shù)s(ω)。

圖3　已加工表面熱源的分布形狀

在不同的磨削工藝參數(shù)下,將求得的已加工表面熱源分布形狀繪于圖3,圖中vs是砂輪轉(zhuǎn)速。由圖3可得,已加工表面熱源的分布形狀隨著磨削工藝條件而改變,將已加工表面熱源的分布形狀假設(shè)為某一特定形狀,并不適用于所有的磨削工況。因此,在利用淺磨模型對磨削溫度場進(jìn)行數(shù)值模擬時,必須根據(jù)具體的磨削工藝條件,計算相應(yīng)的已加工表面熱源分布形狀。

2　磨削溫度場數(shù)值仿真模型

本文采用有限元模擬軟件ANSYS 14.0建立磨削溫度場的數(shù)值仿真模型(淺磨模型),如圖4所示,具體的建模過程如下所述。

2.1　幾何模型及網(wǎng)格劃分

在建立數(shù)值仿真模型時,建立了工件的二維幾何模型。工件的長度是60 mm,高度是12 mm。為了方便加載熱源,工件已加工表面的網(wǎng)格尺寸劃分為磨削接觸弧長的1/30。沿工件的高度方向,劃分了30個網(wǎng)格,并且已加工表面附近的網(wǎng)格劃分得更加細(xì)密。以上網(wǎng)格劃分已通過網(wǎng)格獨立性驗證,足以獲得準(zhǔn)確的計算結(jié)果。單元類型選擇二維八節(jié)點平面熱效應(yīng)單元PLANE77。

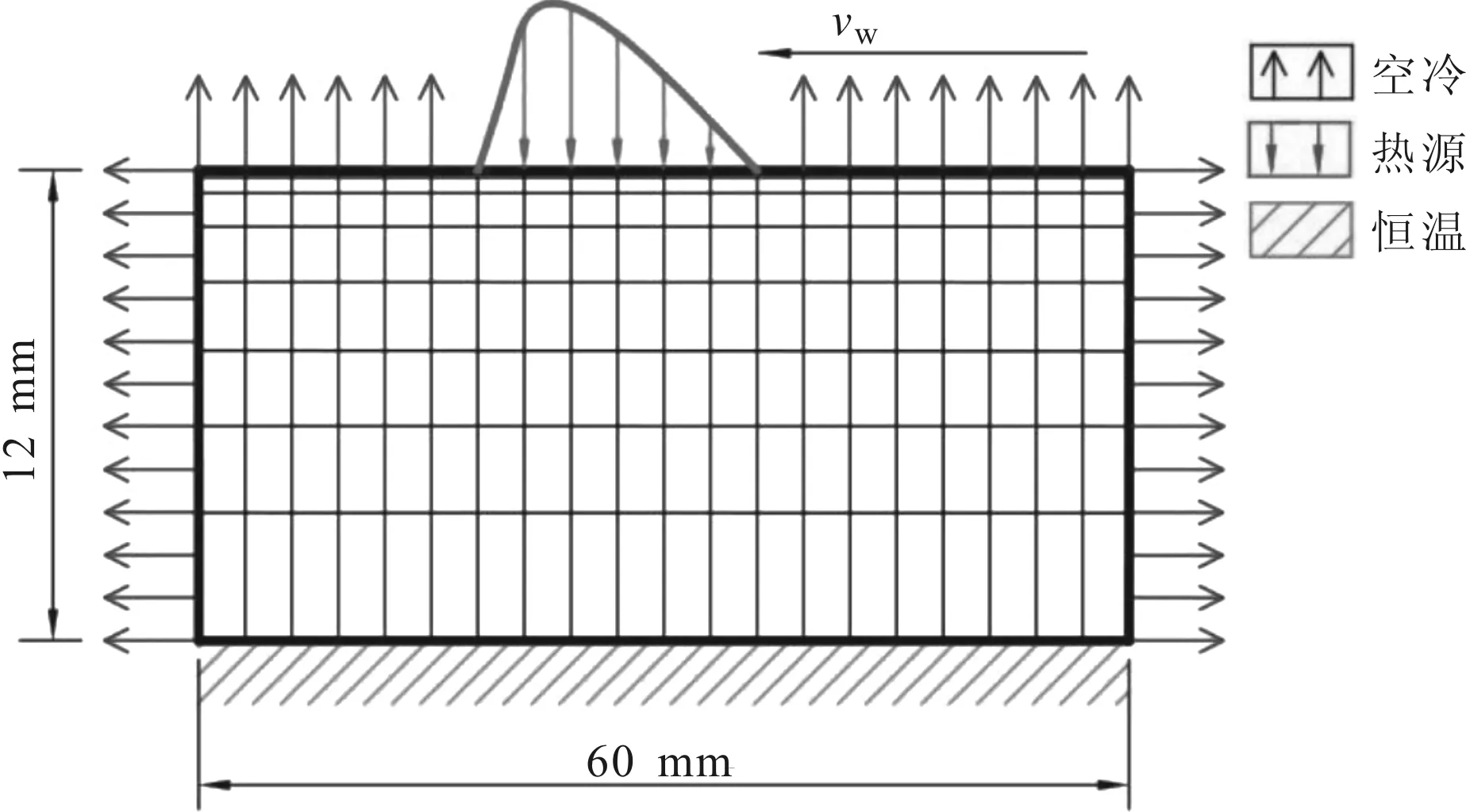
圖4　磨削溫度場數(shù)值仿真建模示意圖

2.2　材料特性

工件材料是淬硬軸承鋼GCr15,砂輪磨粒材料是白剛玉,兩種材料的熱物性參數(shù)如表1所示。

表1　兩種材料的熱物性參數(shù)[11]

注:文獻(xiàn)[11]中的工件材料是AISI 52100,其材料特性接近于GCr15;白剛玉的熱物性參數(shù)用于計算砂輪與工件之間的熱量分配比。

2.3　邊界條件

在建立數(shù)值仿真模型時,將周圍環(huán)境溫度設(shè)置為20 ℃,將工件底面設(shè)置為恒溫絕熱。干磨時,由于工件與周圍環(huán)境之間的對流換熱系數(shù)在20～100 W/(m2·K)之間,并且磨削溫度場的數(shù)值仿真模型對對流換熱系數(shù)的微小變化不敏感,因此將對流換熱系數(shù)設(shè)置為60 W/(m2·K)[12]。

在模擬工件的磨削溫度場時,將已加工表面熱源加載到工件的已加工表面上,如圖4所示。在計算已加工表面熱源的熱流密度分布qwf(ω)時,首先通過磨削實驗測量切向磨削力Ft,再利用式(7)計算砂輪和工件接觸表面上的平均熱流密度

q=Ftvs/(blc)

(7)

式中:b是磨削寬度。

然后分析磨削區(qū)熱量分配關(guān)系,計算砂輪與工件之間的熱量分配比ε[11]和傳入工件的平均熱流密度qw,并且qw=εq,ε的表達(dá)式如下

(8)

式中:kg是磨粒的熱導(dǎo)率;ro是磨粒接觸半徑。

最后計算描述已加工表面熱源分布形狀的形函數(shù)s(ω),并最終得到已加工表面熱源的熱流密度分布qwf(ω)=qws(ω)。

在計算已加工表面熱源的熱流密度分布qwf(ω)時,算得的形函數(shù)s(ω)實際上是m個離散值,并且只有ω∈[-lc,0]內(nèi)的s(ω)離散值參與計算qwf(ω)。因此,算得的qwf(ω)也是一系列的離散值。在進(jìn)行數(shù)值模擬時,將qwf(ω)的離散值施加到已加工表面熱源分布區(qū)域內(nèi)的節(jié)點上。由于沿工件的長度方向網(wǎng)格尺寸劃分為磨削接觸弧長的1/30,那么在已加工表面熱源分布區(qū)域內(nèi)有31個節(jié)點,因此算得的qwf(ω)應(yīng)有31個離散值。為了獲得31個qwf(ω)離散值,在計算形函數(shù)s(ω)時,假設(shè)已加工表面熱源的分布區(qū)域為[-3lc,2lc],并將已加工表面熱源的分布區(qū)域等分為150個區(qū)間,即m=150。

在數(shù)值模擬過程中,已加工表面熱源沿磨削方向步進(jìn),并隨時更新已加工表面的對流換熱條件。

3　磨削力與磨削溫度測量實驗

采用MKL7120×6 CNC強(qiáng)力磨床開展平面磨削實驗,磨削工藝條件如表2所示。在每次磨削之前,都進(jìn)行砂輪修整。采用YDXM-III97型測力儀測量磨削力,采用Ti32型熱成像儀測量磨削溫度,磨削力與磨削溫度測量實驗的示意圖[12]如圖5所示。在測量磨削溫度時,設(shè)置熱成像儀的成像像素為320×240,空間分辨率為1.25×10-3rad,最小焦距為15 cm。

圖5　磨削力與磨削溫度測量實驗示意圖[12]

4　結(jié)果及討論

根據(jù)如表2所示的磨削工藝條件,開展磨削力與磨削溫度測量實驗,計算傳入工件的平均熱流密度qw與已加工表面熱源的形函數(shù)s(ω),并對工件的磨削溫度場進(jìn)行數(shù)值模擬。切向磨削力Ft的實驗測量結(jié)果與平均熱流密度qw的計算結(jié)果如表3所示。

表2　磨削工藝條件

根據(jù)表3中的第1、3、5組磨削工藝參數(shù),將求得的形函數(shù)s(ω)繪于圖6。利用求得的qw與s(ω)

表3　Ft測量值與qw計算值結(jié)果

計算已加工表面熱源的熱流密度分布qwf(ω),利用數(shù)值仿真模型模擬工件的磨削溫度場。在表3中第1組磨削工藝參數(shù)下,溫度場分布的實驗測量結(jié)果與數(shù)值模擬結(jié)果見圖7,發(fā)現(xiàn)兩溫度場分布雖然略有差異,但是總體上較為相近。

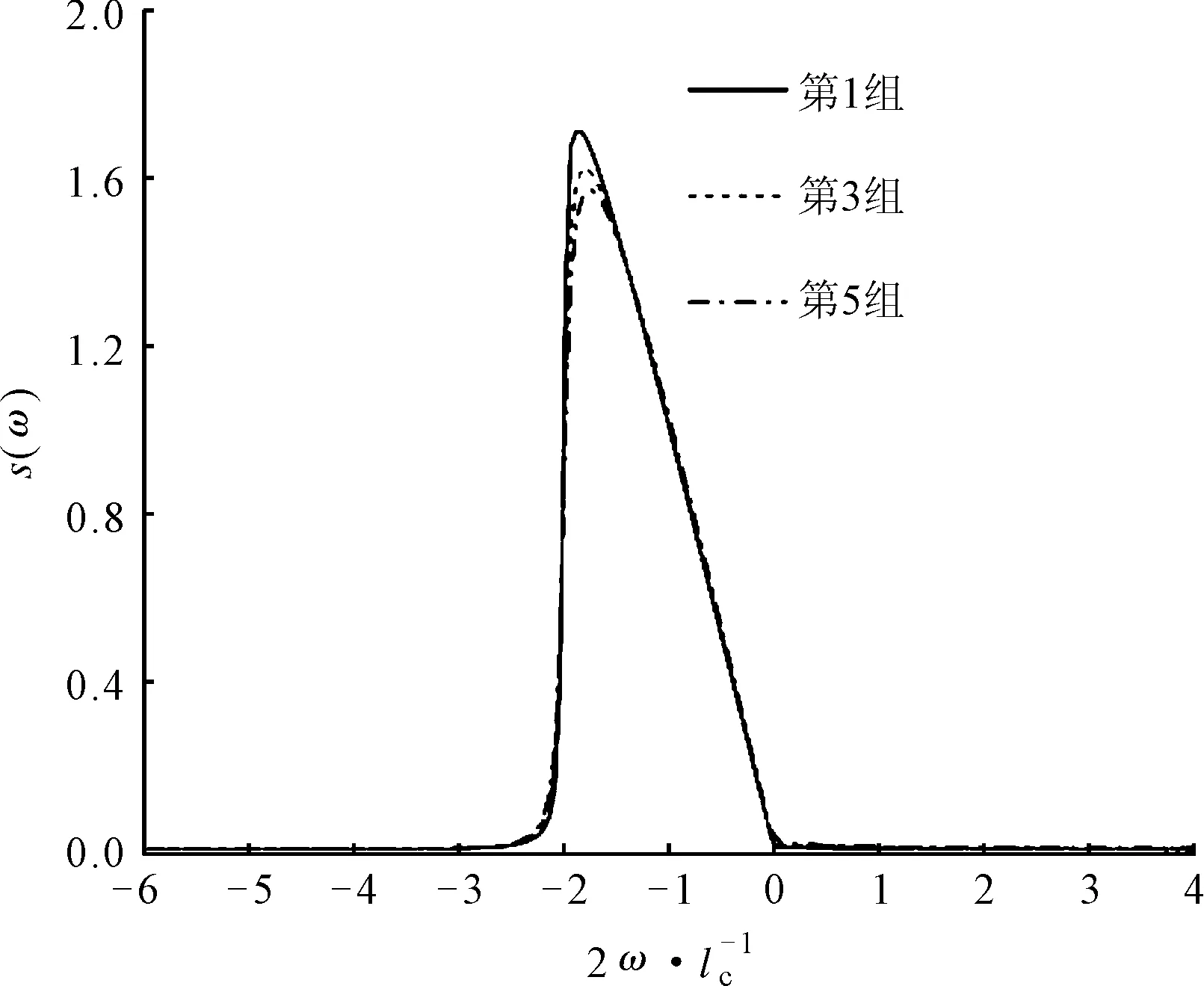
圖6　不同磨削條件下的已加工表面熱源形函數(shù)s(ω)

(a)實驗結(jié)果

(b)模擬結(jié)果圖7　溫度場分布的測量結(jié)果與模擬結(jié)果

圖8　磨削區(qū)已加工表面溫度分布

在表3中第1組磨削工藝參數(shù)下,磨削區(qū)已加工表面溫度分布的測量與模擬結(jié)果見圖8,發(fā)現(xiàn)兩者具有較好的一致性。

在如表3所示的磨削工藝參數(shù)下,磨削區(qū)已加工表面最高溫度的測量與模擬結(jié)果見圖9。利用測量結(jié)果的算術(shù)平均值計算相對誤差,結(jié)果見圖9,發(fā)現(xiàn)最高溫度的模擬值與測量值之間最大相對誤差是9.5%,最小相對誤差是0.8%。

圖9　磨削區(qū)已加工表面最高溫度及相對誤差

5　結(jié)　論

本文建立了已加工表面熱源分布形狀的計算方法,利用淺磨模型計算了磨削溫度場,結(jié)論如下。

(1)已加工表面熱源的分布形狀隨著磨削工藝條件而改變,將已加工表面熱源的分布形狀假設(shè)為某一特定形狀,并不適用于所有的磨削工況。

(2)建立的磨削溫度場數(shù)值仿真模型(淺磨模型)可以準(zhǔn)確地模擬工件的磨削溫度場,磨削區(qū)已加工表面最高溫度的模擬值與測量值之間相對誤差在0.8%～9.5%之間。

(3)利用淺磨模型對磨削溫度場進(jìn)行數(shù)值模擬時,采用本文方法不需預(yù)先假設(shè)已加工表面熱源的分布形狀,即可根據(jù)具體的磨削條件,獲得相應(yīng)的熱源分布形狀。

參考文獻(xiàn):

[1]MALKIN S, GUO C. Thermal analysis of grinding [J]. CIRP Annals-Manufacturing Technology, 2007, 56(2): 760-782.

[2]ANDERSON D, WARKENTIN A, BAUER R. Comparison of numerically and analytically predicted contact temperatures in shallow and deep dry grinding with infrared measurements [J]. International Journal of Machine Tools and Manufacture, 2008, 48(3): 320-328.

[3]ANDERSON D, WARKENTIN A, BAUER R. Experimental validation of numerical thermal models for dry grinding [J]. Journal of Materials Processing Technology, 2008, 204(1): 269-278.

[4]MAHDI M, ZHANG L. The finite element thermal analysis of grinding processes by ADINA [J]. Computers & Structures, 1995, 56(2/3): 313-320.

[5]WANG X, YU T, SUN X, et al. Study of 3D grinding temperature field based on finite difference method: considering machining parameters and energy partition [J]. International Journal of Advanced Manufacturing Technology, 2016, 84(5/6/7/8): 915-927.

[6]SHAH S M, NELIAS D, CORET M. Numerical simulation of grinding induced phase transformation and residual stresses in AISI-52100 steel [J]. Finite Elements in Analysis and Design, 2012, 61: 1-11.

[8]ROWE W B, JIN T. Temperatures in high efficiency deep grinding (HEDG) [J]. CIRP Annals-Manufacturing Technology, 2001, 50(1): 205-208.

[9]JAEGER J C. Moving sources of heat and the temperature of sliding contacts [J]. Proceeding of the Royal Society of New South Wales, 1942, 76: 203-224.

[10] GUO C, MALKIN S. Inverse heat transfer analysis of grinding: part 1Methods [J]. Journal of Engineering for Industry, 1996, 118: 137-142.

[11] ROWE W B. Thermal analysis of high efficiency deep grinding [J]. International Journal of Machine Tools and Manufacture, 2001, 41(1): 1-19.

[12] 王德祥, 葛培琪, 畢文波, 等. 磨削弧區(qū)熱源分布形狀研究 [J]. 西安交通大學(xué)學(xué)報, 2015, 49(8): 116-121.

WANG Dexiang, GE Peiqi, BI Wenbo, et al. Heat source profile in grinding zone [J]. Journal of Xi’an Jiaotong University, 2015, 49(8): 116-121.