超聲載荷下TC4鈦合金的疲勞壽命分析

蘇勝，郭利軍，張東博，高琦，王彤宇

?

超聲載荷下TC4鈦合金的疲勞壽命分析

蘇勝1，郭利軍2，張東博1，高琦3，王彤宇1

(1. 長春理工大學機電工程學院，吉林長春 130022；2. 凌云科技集團有限責任公司，湖北武漢 430040； 3. 中國科學院聲學研究所東海研究站，上海 201815)

通過計算裂紋尖端應力強度因子及疲勞裂紋擴展速率d/d，由C. Paris模型推導出安全壽命N，由Bathias公式計算“啞鈴”狀鈦合金試樣的裂紋擴展壽命。通過理論計算和有限元分析超聲疲勞“啞鈴”狀試樣，得出應力最大位置。利用有限元仿真和實驗數據分析TC4鈦合金疲勞壽命。在20 kHz的超聲疲勞試驗中，試樣的斷口位置表明：TC4鈦合金材料內部缺陷是試樣萌生裂紋使斷裂位置偏離最大應力處的主要原因。并得出疲勞裂紋萌生階段壽命決定“啞鈴”狀試樣的疲勞壽命。

疲勞壽命；應力強度因子；有限元；斷裂力學

0 引言

隨著工業技術的發展，諸多工程應用，如航空航天、鐵路運輸、生物醫學等，其材料和構件常面臨長時間、低幅載荷的重復作用，載荷次數高達千兆次，極易產生疲勞[1]，造成重大的安全事故。例如：2007年，美軍F-15C鷹式戰斗機在做空中纏斗飛行訓練時，因桁梁出現了金屬疲勞問題，突然凌空解體。因此，研究超高周循環載荷作用下材料的疲勞行為和發生機理比較重要。

在臨床應用中，超聲手術刀具有刀口整齊、止血快、熱損傷區域小、產生煙霧少、療效好等優點，迅速成為超聲外科臨床介入治療的重要手段[2]。對于頻率=55 kHz的超聲手術刀，工作1小時就經受了2×108次超高周振動。為了避免因超聲手術刀疲勞斷裂而造成的醫療事故，目前臨床中采用超聲手術刀使用一次即丟棄的方案。因此，開展超聲手術刀疲勞特性的研究，探索超聲刀疲勞壽命的評估方法，提高超聲刀的抗疲勞性能[3-6]，延長手術刀的使用壽命，以確保手術的安全性，具有重要的意義。

在傳統的疲勞試驗中，設計試樣默認材料為均勻連續介質[7]，主要是根據材料的曲線，運用線性累計損傷理論來估計構件的疲勞壽命，沒有考慮材料缺陷(如表面劃痕、金屬夾雜、腐蝕坑、鍛造缺陷等)造成的各種類型的裂紋。帶著這種裂紋的構件，在交變載荷下，即使載荷低于材料本身的疲勞強度極限，裂紋也會很快擴展并斷裂。本文以斷裂力學為依據，將構件裂紋根部的材料元取出，制成光滑的疲勞試樣。在超聲載荷作用下進行疲勞試驗，用以模擬構件受交變應力時鈦合金的疲勞行為。通過研究鈦合金的應力疲勞行為以及萌生裂紋時的擴展速率，計算出試樣的疲勞壽命。通過裂紋尖端應力強度因子，分析裂紋擴展壽命與總壽命的關系。為提高結構件的抗疲勞性能和延長結構件的使用壽命，提供參考依據。

1 疲勞試樣的制備

1.1 試驗材料

試樣材料是從寶雞金屬加工廠購買的TC4(Ti- 6Al-4V)合金棒材。其主要化學成分(質量分數，%)和力學性能見表1和表2。表2中，是彈性模量，σ是抗拉強度，σ是屈服強度是斷面收縮率。

表1 試樣的化學成分(%)

表2 材料的力學性能

1.2 試樣的理論計算

在拉伸疲勞試驗中，疲勞試樣必須滿足諧振條件。為了縮短試樣長度并加速疲勞試驗，試樣通常設計為“啞鈴”狀，如圖1所示。

圖1 啞鈴狀試樣

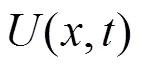
式中，E為材料的動態彈性模量。

設試樣沿軸向各段的截面面積為：

為了獲得最大的應力放大系數，使試樣中間圓柱段的長度不為零。TC4的諧振長度、應力應變場及材料特性決定了試樣的幾何尺寸。

設試樣滿足諧振條件，通過參照文獻[8]中的設計方法，用分離變量法解方程，得出當“啞鈴”狀試樣中間設計為圓柱形時，具有較高的應力放大系數的結論，可通過解析計算獲得這種試樣的諧振長度。經計算得出本文使用的超聲疲勞試樣的幾何尺寸，如表3所示。

表3 試樣幾何尺寸(單位：mm)

1.3 試樣的仿真分析

對稱的超聲疲勞試樣(如圖1所示)兩端自由，通過數值分析可以得出最大應力位于試樣中間的圓柱截面，試樣端部保持最大位移值，圓弧中間點最大應力處為振動位移節點，應力最大時，位移最小(如圖2所示)。試樣沿軸方向位的位移大小和應力值歸一化后如圖3所示。

圖2 試樣振動位移云圖

圖3 試樣形變和應力值

一般疲勞循環在105周次以上稱為高周疲勞[9]，對于具有明顯缺陷(如夾雜、縮孔)的材料，疲勞破壞常源于缺陷處[10]。所以，盡量選取中間為圓柱段的試樣，這樣即使最大缺陷不在試樣中間，試樣的疲勞斷裂也會在接近最大應力處發生。

2 疲勞壽命分析

2.1 疲勞裂紋擴展速率估算

疲勞壽命由疲勞裂紋形成和裂紋擴展兩部分決定。當疲勞裂紋起裂并擴展時，超聲波在試樣材料連續體中傳播，而在裂紋面上反射，導致裂紋閉合效應減小，裂紋尖端的塑性區也較小[11]。本文測量得到了斷口處裂紋萌生區域從初始裂紋半徑()到第一擴展區半徑(0)，引用C. Paris模型預測超聲疲勞實驗條件下TC4材料的疲勞裂紋擴展速率為[12]

對式(4)采用Euler數值積分的方法得到TC4試樣的疲勞壽命[12]：

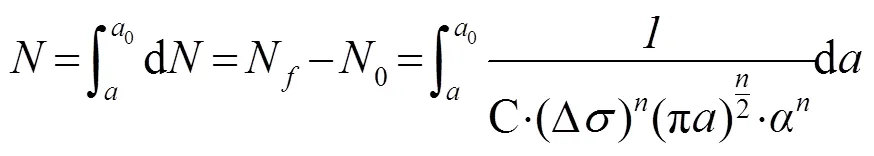
對式(5)進行計算得出N=7.46×109，對數壽命為lgN=9.872。

2.2 疲勞壽命有限元仿真分析

采用有限元軟件疲勞模塊分析，設置參數為：應力比-1，20 kHz，max=330 MPa，由此得到的疲勞仿真結果如圖4所示。通過數值分析獲得試樣在循環1.70×109周次時的對數壽命為lgN= 9.230，這與式(5)中的計算結果相接近。壽命最小處為試樣中間段區域，說明此區域最先出現疲勞裂紋，最后使試樣斷裂。

圖4 試樣疲勞壽命云圖

3 試驗及其結果分析

3.1 疲勞試驗系統

如圖5所示，超聲疲勞試驗系統由超聲發生器、超聲換能器、位移放大器、試樣、測控系統(計算機控制系統、激光位移傳感器)和冷卻系統組成。

圖5 超聲疲勞試驗系統

試驗時，試件在超聲波作用下發生軸向受迫振動，系統的振動頻率在(20±0.5) kHz范圍內，根據試樣材料的基本力學性能，設置應力幅值為330 MPa，用激光測振儀探測試樣表面裂紋。試驗過程中試樣發熱，用紅外熱像儀測得實驗過程中試樣的表面溫度。為避免對試驗結果造成影響，冷卻系統為恒溫水域，控制試樣溫度在60℃左右。

3.2 斷口分析

當試件出現疲勞裂紋時，試件諧振頻率下降，系統諧振狀態發生變化，試件有刺耳的聲音發出，系統報警，此時記錄試驗循環周次及應力水平等數據，直至試樣斷裂再次記錄。

在超高周循環下，試樣的疲勞斷裂更易從試件內部缺陷處開始，超聲疲勞試驗裂紋多數發生在試樣的外表面[4]。盡管有些夾雜、縮孔等缺陷并不在試樣中間最大應力處，但疲勞破壞仍會從這些缺陷處起裂。圖6所示為TC4“啞鈴”狀試樣在頻率為20 kHz超聲疲勞試驗中發生疲勞斷裂的情形，試樣的疲勞破壞明顯偏離試樣的最大應力處。

在掃描電子顯微鏡下對超聲疲勞試樣斷口進行觀察，結果發現：超聲疲勞試樣的裂紋有內部萌生和表面萌生兩種機制。圖7顯示了裂紋萌生時，初始裂紋形成位置一般有夾雜物。內部初始裂紋所受約束較大而且不受外部環境的影響，研究表明裂紋內部萌生疲勞極限高于裂紋表面萌生疲勞極限[13]。如圖7(a)所示，材料內部疲勞裂紋附近產生二次裂紋所需的時間更久。超聲負載試驗中，疲勞裂紋從試樣表面萌生。在下列情況下，裂紋萌生位置由表面轉入內部：(1) 材料內部有尺寸較大的夾雜物缺陷；(2) 材料表層硬度遠高于內部或試樣表面存在殘余壓應力，如圖7(b)所示。圖8為某試樣斷口的形貌，圖9為其細節圖。由圖8、9可知，在A區域產生了二次裂紋，當位錯塞積形成的應力達到理論斷裂強度時，滑移帶在晶界上引起的應變不斷增加，晶界開裂形成二次裂紋。疲勞裂紋擴展的解理面及疲勞裂紋附近的二次裂紋并沒有和初始裂紋聚合在一起。在超聲負載下，材料疲勞總是在應力最高、強度最弱的局部位置上形成。疲勞源常萌生于層片板條界面，TC4域團間的二次裂紋并不擴展。

圖6 試樣斷裂后的照片

圖7 試樣斷裂位置-1

圖8 試樣斷裂位置-2

圖9 試樣斷裂位置-2的細節圖

本文實驗過程中發現，材料裂紋萌生位置在材料內部。文獻[14]表明，在超高周疲勞試驗中，裂紋萌生的位置在材料內部產生。試樣斷裂的位置偏離應力圓柱中間最大應力處。通過對疲勞斷口進行分析發現，斷口處材料存在夾雜物，如圖7(b)所示。因此，材料內部裂紋缺陷并不產生在試樣最大應力處，但疲勞裂紋仍會從這些缺陷處產生。

3.3 試驗數據分析

表4給出了本次試驗的試驗數據結果，在超聲波金屬探傷儀中，由于編號1、2的試樣顯示有微弱的回波，其余試樣無回波，可見材料的內部缺陷降低了試樣的疲勞壽命。仿真分析默認材料是均勻的連續介質，仿真分析結果與試驗數據對比結果表明，試樣(編號為3、4、5、6)的疲勞壽命接近于數值分析結果。

表4 TC4試樣的超高周疲勞試驗結果

對表4數據利用文獻[15]的方法，得出應力值為330 MPa、斷裂率為50%、95%、99%時試件的安全壽命分別為：

本文根據Bathias的推導，在=330 MPa應力值條件下，裂紋擴展階段壽命N可表示為[12]

表5 TC4試樣疲勞壽命試驗結果比較

4 結論

本文通過數值分析計算，獲得了超聲疲勞“啞鈴”狀試樣的幾何尺寸及疲勞壽命，對比試驗數據結果，傳統的計算方法默認裂紋頂端局部疲勞應變，本文通過分析裂紋局部應變，得出如下結論：

(1) 材料內部裂紋缺陷是試樣萌生疲勞裂紋使斷裂位置偏離最大應力處的主要原因；

(2) TC4“啞鈴”狀試樣的疲勞壽命主要是由疲勞裂紋萌生階段決定，裂紋擴展壽命占安全壽命的比重很小。

[1] WANG Qingyuan, BATHIAS C, KAWAGOISHI N, et al. Effect of inclusion on subsurface crack initiation and gigacycle fatigue strength[J]. International Journal of Fatigue, 2002, 24(12): 1269- 1274.

[2] 周紅生, 許小芳, 程茜, 等.超聲手術刀的優化設計[J]. 聲學技術, 2012, 31(5): 48-52. ZHOU Hongsheng, XU Xiaofang, CHENG Qian, et al. The optimum design of ultrasonic scalpel[J]. Technical Acoustics, 2012, 31(5): 48-52.

[3] GAO Yukui，YAO Mei，SHAO Peige. Another mechanism for fatigue strength improvement of metallic parts by shot peening[J]. J Mater Eng Perform, 2003, 12(4): 507-511.

[4] WU Yanzeng ,WANG Qingyuan, OUYANG Qianlin. Influence of subjection to plasma nitriding surface modifications on ultra-high cycle fatigue behavior of Ti-6Al-4V[J]. Applied Mechancis and Materials, 2012, 105-107(4): 1731-1735.

[5] NIKITIN A, Bathias C. Crack path in aeronautical titanium alloy under ultrasonic torsion loading[J]. Frattura ed Integrita Strutturale, 2016, 10(35): 213-222.

[6] 李慶芬. 斷裂力學及其工程應用[M]. 哈爾濱: 哈爾濱工業大學出版社, 2007: 132-175. LI Qingfen. Fracture mechanics and engineering application[M]. Harbin: Harbin Institute of Technology Press, 2007: 132-175.

[7] 陳傳堯. 疲勞與斷裂[M]. 武漢: 華中科技大學出版社, 2008: 130-150. CHEN Chuanyao. Fatigue and fracture[M]. Wuhan: Huazhong University of Science and Technology Press, 2008: 130-150.

[8] 薛紅前, 陶華, BATHIAS C. 超聲疲勞試樣設計[J]. 航空學報, 2004, 25(4): 425-429. XUE Hongqian, TAOHua, BATHIAS C.Ultrasonic fatigue specimen design[J]. Acta Aeronautica Et Astronautica Sinica, 2004, 25(4): 425-429.

[9] 王清遠, 劉永杰. 結構金屬材料超高周疲勞破壞行為[J]. 固體力學學報, 2010, 31(7): 496-503. WANG Qingyuan, LIU Yongjie. Ultra-high cycle fatigue behavior of structural metal materials[J]. Chinese Journal of Solid Mechanics, 2010, 31(7): 496-503.

[10] 中國航空研究院. 應力強度因子手冊[M]. 北京: 科學出版社, 1981: 396-400. China Aviation Research Institute. Stress intensity factor manual [M]. Beijing: Science Press, 1981: 396-400.

[11] 張安哥, 朱成久. 疲勞、斷裂與損傷[M]. 成都: 西南交通大學出版社, 2006: 99-107. ZHANG Ange, ZHU Chengjiu. Fatigue、fracture and damage [M]. Chengdu: Southwest Jiaotong University Press, 2006: 99-107.

[12] BATHIAS C, PARIS C. Gigacycle fatigue in mechanical practice [M]. Newyork: Marcel Dekker, 2005: 105-180.

[13] 楊王玥, 強文江. 材料力學行為[M]. 北京: 化學工業出版社, 2009: 74-127. YANG Wangyue, QIANG Wenjiang. Mechanical behavior of materials[M]. Beijing: Chemical Industry Press, 2009: 74-127.

[14] 胡燕慧, 張崢, 鐘群鵬, 等. 金屬材料超高周疲勞研究進展[J]. 機械強度, 2009, 31(6): 979-985. HU Yanhui, ZHANG Zheng, ZHONG Qunpeng, et al. Research progress on ultrahigh cycle fatigue of metal materials[J]. Journal of Mechanical Strength, 2009, 31(6): 979-985.

[15] 鄭修麟. 金屬疲勞的定量理論[M]. 西安: 西北工業大學出版, 1994: 168-200. ZHENG Xiulin. Quantitative theory of metal fatigue[M]. Xi'an: Northwest University of Technology, 1994: 168-200.

Fatigue life analysis of TC4 titanium alloy under ultrasonic loading

SU Sheng1, GUO Li-jun2, ZHANG Dong-bo1, GAO Qi3, WANG Tong-yu1

(1. School of Mechatronical Engineering Changchun University of Science and Technology, Changchun 130022, Jilin, China;2. Ling Yun Science＆Technology Group CO. LTD.,Wuhan 430040,Hubei,China;3.Shanghai Acoustics Laboratory,Chinese Academy of Sciences, Shanghai 201815, China)

The position of maximum stress in the ultrasonic fatigue test of dumb-bell shaped TC4 titanium alloy specimen is determined by theoretical calculation and the finite element simulation. In the 20 kHz ultrasonic fatigue test, the fracture position of the specimen shows that the internal defect of TC4 material is the main reason of the crack initiation to make the fracture position deviated from the maximum stress position. The fatigue life of TC4 is analyzed by finite element simulation and experimental data. By calculating the stress intensity factor at crack tip and the fatigue crack growth rate, the safety lifeNis derived from the C.Paris model. The Bathias formula is used to calculate the crack propagation life of the dumb-bell shaped specimen, and the fatigue life of the specimen is determined by the crack initiation life.

fatigue life; stress intensity factor; finite element; fracture mechanics

TB553

A

1000-3630(2018)-01-0057-05

10.16300/j.cnki.1000-3630.2018.01.010

2017-11-15;

2018-01-23

國家自然科學基金項目(11474042、11774382、11574348)

蘇勝(1987－), 男, 吉林長春人, 碩士, 研究方向為現代機械設計理論與方法。

王彤宇, E-mail: wty_salas@126.com