一種快速求解寬頻簡正波的方法

朱飛龍，李風華，Eric I. Thorsos

?

一種快速求解寬頻簡正波的方法

朱飛龍1,2，李風華1，Eric I. Thorsos3

(1. 中國科學院聲學研究所聲場聲信息國家重點實驗室，北京 100190；2. 中國科學院大學，北京 100049；3.Applied Physics Laboratory, University of Washington WA, 98105 USA)

針對寬帶信號的簡正波解，傳統的求解簡正波數值方法常常需要重復計算本征值方程，計算效率低。文中將頻率的變化當作擾動，提出利用微擾理論得到參考頻率附近的簡正波解。該方法具有直接、精確、高效的特點，計算得到的水平波數和本征函數與KRAKENC程序計算結果吻合較好，兩種方法計算得到的脈沖波形最大相關系數大于0.97。

微擾理論；簡正波；寬帶信號；脈沖波形

0 引言

簡正波方法在水聲學中有著廣泛的應用。自從Pekeris最早于1948年發表了關于簡正波的理論[1]后，簡正波方法取得了長足的發展。簡正波方法的最初應用，就是準確求解本地簡正波的本征值和本征函數。除了少數理想的波導可以得到簡正波的解析解外，大部分實際應用都需要借助現有程序得到簡正波的數值解。現在得到廣泛應用的求解簡正波的程序有KRAKEN[2]，適用于深海環境的廣義相積分簡正波[3]和適用淺海環境的波束位移射線簡正波(Beam Displacement Ray Mode，BDRM)[4]方法也可以快速地得到簡正波解。

在考慮寬頻信號的時候，比如1/3倍頻程帶寬，上述傳統的程序需要多次重復計算簡正波的本征方程，計算效率低。為此針對吸收性波導環境，王寧等[2]提出了哈密頓方法，通過降低本征值搜索維度，一定程度上提高了簡正波的求解速度，并將該方法應用到求解寬頻信號的簡正波[6]。很多學者提出了間接求解寬頻簡正波的方法。Robert等[7]通過對本征函數進行分解，在參考頻率的簡正波已知時，利用蓋勒金方法得到寬帶信號簡正波的近似解，但是該方法的精度不高。王寧等[8]將本征值問題轉化成動態系統問題，通過矩陣運算，直接得到了參考頻率附近頻率的簡正波解。Tindle等[9]針對海水聲速剖面水平變化的環境，利用微擾理論直接得到了本地簡正波解。本文提出一種由微擾理論直接得到寬帶信號簡正波解的方法。

1 微擾簡正波理論

在水平不變波導環境下，分層介質中假定各層內的密度是常數，此時深度分離的本征值方程[10]

在有限海深環境下，本征值方程式(1)有無窮多個離散解。當波導環境不存在吸收時，本征值和本征函數都是實數，并且本征函數相互正交，構成一個完備集[11]。當海底存在吸收時，本征值和本征函數是復數，此時本征函數滿足不含復共軛的雙正交歸一性(Bi-orthogonality)[12-13]，即

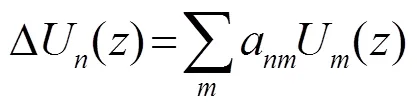
新的簡正波同樣要滿足本征方程，將新的參數值代入式(1)中，忽略二階微擾項，化簡后得到本征水平波數變化量為

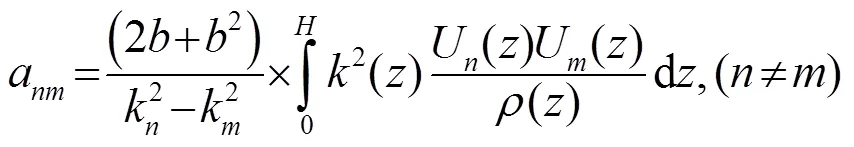
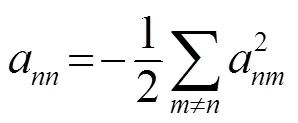
2 淺海波導環境

建立如表1所示的淺海水平不變波導，為了計算方便，在基底厚度50 m處人為加入真空層。參考簡正波的本征值和本征函數由KRAKENC方法計算得到，對應的參考頻率為中心頻率800 Hz。聲場計算中的簡正波號數為30，其中包含25號波導模式簡正波。在微擾法計算中使用的簡正波號數為40。

表1 淺海波導環境參數

2.1 單頻驗證

注意到在圖1中，頻率850 Hz時本征水平波數的誤差比750 Hz時的誤差大。主要是因為隨著頻率增加，前40號簡正波內正則模式簡正波(波導模式和耗散模式簡正波)[14]數量也會增加，增加的簡正波來自于更高號的耗散模式簡正波。但是微擾法得到的簡正波正則模式和連續模式數量不變，所以會導致高號簡正波特別是高號正則模式簡正波的誤差較大。

相反，當頻率減小時，前40號簡正波內正則模式簡正波數量減少，而微擾法保持了正則模式簡正波的數量，所以依然能得到相對較高精度的本地簡正波。因此增加簡正波的號數，以及適時插入本地真實的簡正波可以提高計算精度。

圖2給出了在頻率850 Hz下，本文方法與KRAKENC方法計算得到的第10號簡正波本征函數值的對比。從圖2中看出，微擾法近似結果與KRAKENC方法計算得到的結果吻合很好。

綜上結果可知，本文提出的微擾法得到的簡正波解與KRAKENC方法直接計算得到的結果吻合較好，精度較高。此外，在MATLAB程序中，本文方法計算一次簡正波的時間約為0.47 s；而在相同環境下，KRAKENC方法計算一次簡正波時間為57.35 s，是本文方法的100倍，可見本文方法計算效率很高。

圖1 水平波數估計值與KRAKENC方法計算結果對比，參考頻率800 Hz

圖2 頻率850 Hz下，第10號簡正波本征函數值對比，參考頻率800 Hz

2.2 脈沖波形

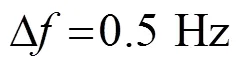
從圖3看出，兩種方法結果吻合很好。根據波形相關系數公式

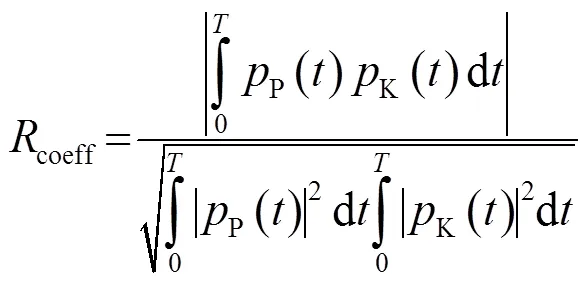
其中：是由微擾法得到的時域波形；是由KRAKENC方法計算得到的時域波形；T是逆傅里葉變換得到的時域波形周期。計算得到兩種方法的波形相關系數，顯然結果是非常精確的。其中本文方法所用時間為98.16 s，KRAKENC方法計算結果所用時間為6 805 s，是本文方法的70倍。

3 深海環境驗證

建立深海水平不變波導環境，海水深度為4 000 m，一次實測的海水聲速剖面如圖4所示。海底參數如表2所示，為了計算方便，在基底厚度505 m處人為地加入了真空層。參考中心頻率為100 Hz，聲場計算中包含了150號簡正波，用于微擾法計算的簡正波號數為200。

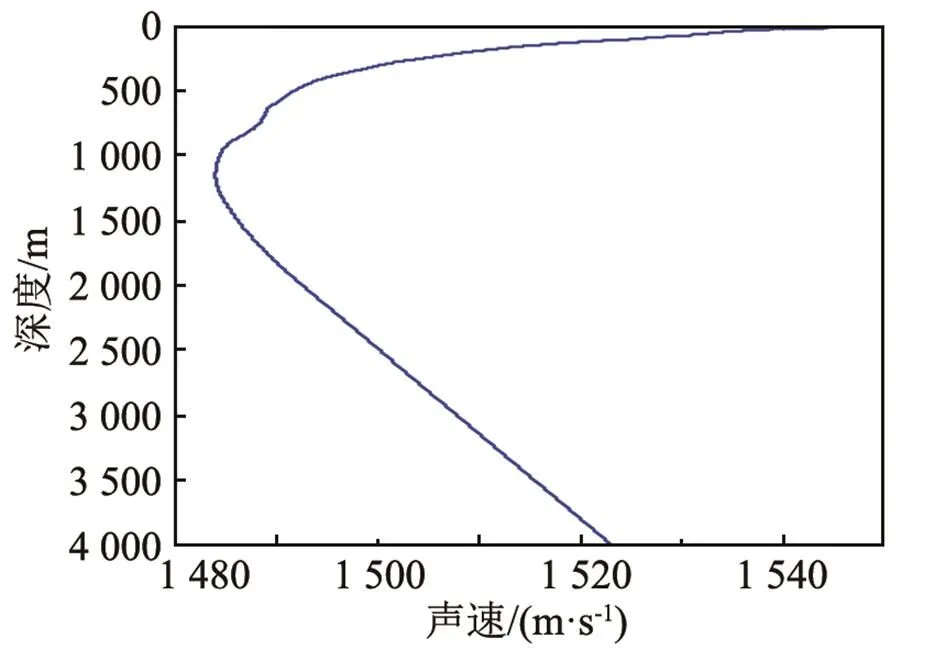
圖4 海水聲速剖面

位于200 m深度的脈沖聲源，中心頻率為100 Hz，帶寬為20 Hz。圖5給出了在距離60 km、接收深度1 000 m處，由本文方法得到的時域波形與KRAKENC方法計算結果的對比。從圖5中看出，兩種方法的波形結果吻合較好，并且兩個時域波形的最大互相關系數約為0.91。當只取峰值到達附近的波包時，兩種結果的波形最大互相關系數可以達到0.972，這樣的精度可以滿足大部分聲場計算的需求。此外，在深海環境下，本文一次簡正波計算時間為2.4 s，而KRAKENC方法計算時間則約為76.4 s，是本文方法的30倍。

表2 深海海底參數

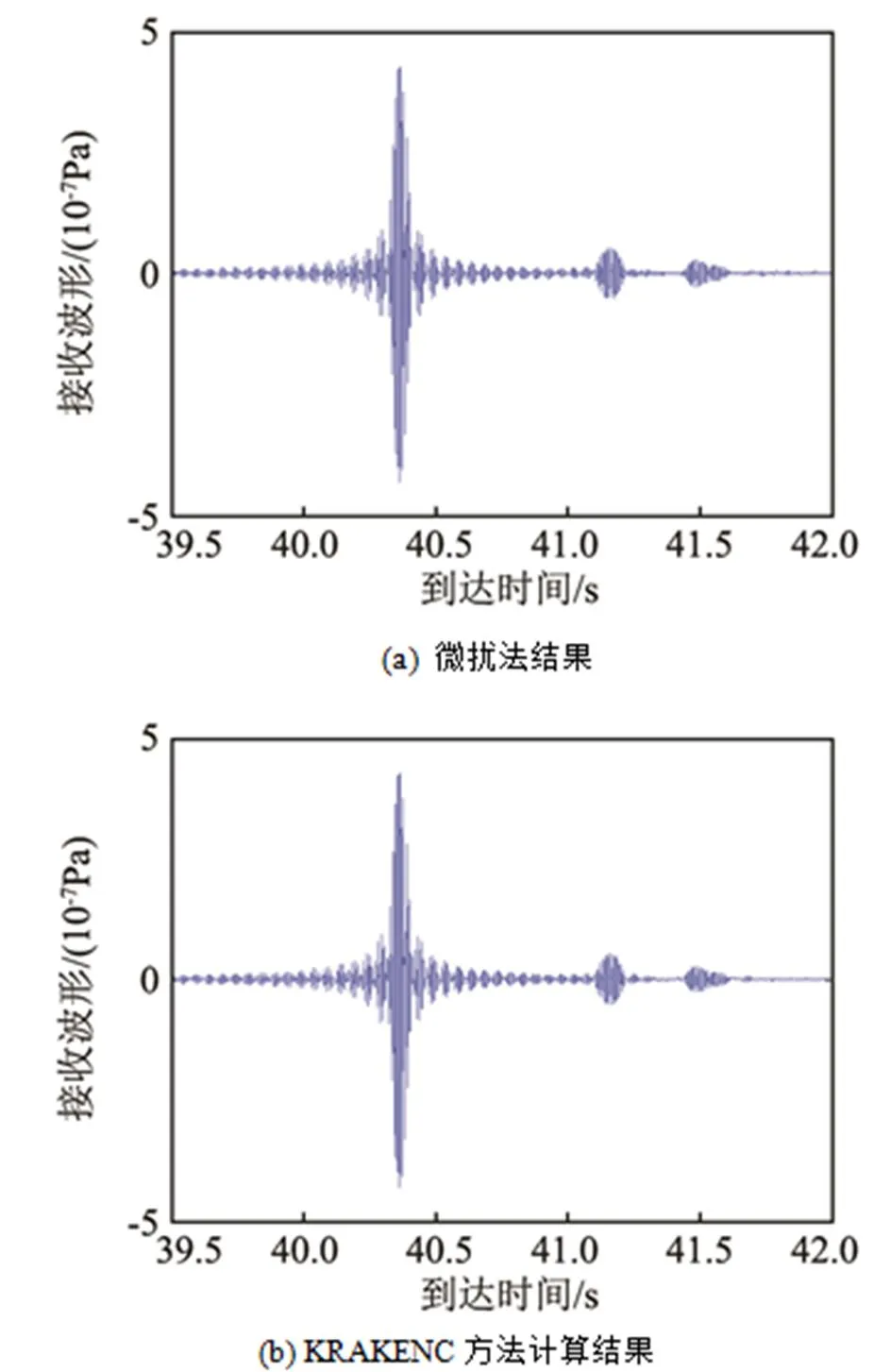
圖5 接收時域波形，聲源深度200 m，中心頻率100 Hz，帶寬20 Hz，接收距離60 km，接收深度1 000 m

4 結論

本文利用微擾理論，提出了一種快速求解寬帶信號簡正波的方法。本文方法有以下優點：

(1) 可以直接得到參考頻率附近簡正波的本征值和本征函數，適用于深海和淺海波導環境，應用范圍廣；

(2) 計算速度快，一次簡正波的計算時間比KRAKENC方法快30倍以上；

(3) 計算精度較高，本文方法得到的簡正波水平波數和本征函數與KRAKENC方法計算結果吻合較好，在淺海環境下得到的時域脈沖波形與KRAKENC方法計算結果最大相關系數為0.99，在深海環境下，峰值所在的波包最大相關系數大于0.97。

[1] PEKERIS C L. Theory of propagation of explosive sound in shallow water[J]. Geol. Soc. Am. Mem, 1948, 27: 1.

[2] PORTER M B. The KRAKEN Normal Mode Program. 2009. http://oalib.hlsresearch.com/Modes/AcousticsToolbox/manualtml/kraken. html.

[3] 張仁和, 何怡, 劉紅. 水平不變海洋聲道中的 WKBZ 簡正波方法[J]. 聲學學報, 1994, 19(1): 1-12. ZHANG Renhe, HE Yi, LIU Hong. WKBZ mode approach to sound propagation in horizontally stratified oceans[J]. Acta Acustica, 1994, 19(1): 1-12.

[4] ZHANG Renhe, LI Fenghua. Beam-displacement ray-mode theory of sound propagation in shallow water[J]. Science in China(Series A), 1999, 42(7): 739-749.

[5] WANG N, WANG H Z. A Hamiltonian solver for finding modal eigenvalues[J]. J. Comput. Acoust., 2010, 18(3): 259-266.

[6] WANG Haozhong, WANG Ning, GAO Dazhi. A Hamiltonian method for finding broadband modal eigenvalues[J]. J. Acoust. Soc. Am., 2012, 131(2): 1047-1054.

[7] ROBERT A K, KNOBLES D P. A practical application of the Galerkin method to the broadband calculation of normal modes for underwater acoustics[J]. J. Acoust. Soc. Am., 1995, 98(3): 1682- 1698.

[8] WANG Ning, LIU Jin zhong. New approach to the normal mode method in underwater acoustics[J]. Chinese Physics, 2002, 11(5): 456-460.

[9] TINDLE C T, O’ DRISCOLL L M, HIGHAM C J. Coupled mode perturbation theory of range dependence[J]. J. Acoust. Soc. Am., 2000, 108(1): 76-83.

[10] JENSEN F B, KUPERMAN W A, PORTER M B, et al. Computational ocean acoustics[M]. 2ndedition. New York: Springer, 2011.

[11] WILCOX C H. Sound Propagation in stratified fluids[M]. New York: Springer, 1984, Chaper 2, Section 1: 13-17, Chaper 3, Section 9: 104-116.

[12] FRIEDMAN B. Principles and techniques of applied mathematics [M]. New York: Wiley, 1956: Chapter 4.

[13] WAXLER R. A vertical eigenfunction expansion for the propagation of sound in a downward-refracting atmosphere over a complex impedance plane[J]. J. Acoust. Soc. Am., 2002, 112(6): 2540-2552.

[14] BUCKINGHAM M J, GIDDENS E M. On the acoustic field in a Pekeris waveguide with attenuation in the bottom half-space[J]. J. Acoust. Soc. Am., 2006, 119(1): 123-142.

A fast method for broadband normal mode computation

ZHU Fei-long1,2, LI Feng-hua1, Eric I. Thorsos3

(1. State Key Laboratory of Acoustics, Institute of Acoustics, Chinese Academy of Sciences, Beijing 100190, China;2. University of Chinese Academy of Sciences, Beijing 100049, China;3. Applied Physics Laboratory, University of Washington WA, 98105, USA)

For the broadband normal mode computation, conventional normal mode numerical code needs to be used repeatedly, which lowers the computational efficient. Viewing the change of frequency as perturbation, a fast method based on perturbation theory is presented in this paper. This method is direct, fast and accurate. Numerical simulations in shallow water and deep ocean are performed, the calculated horizontal wave-numbers and modal eigen-functions by this method agreewell with those obtained by KRAKENC method, and the maximum cross correlation between the impulse waveforms calculated by thetwo methods is greater than 0.97.

perturbation theory; normal mode; broadband signal; impulse waveform

O427

A

1000-3630(2018)-01-0038-05

10.16300/j.cnki.1000-3630.2018.01.007

2017-04-21;

2017-06-19

國家自然科學基金資助項目(11125420)

朱飛龍(1989－), 男, 江西贛州人, 博士研究生, 研究方向為水聲物理。

李風華, E-mail: lfh@mail.ioa.ac.cn