基于貝葉斯定理的異重流水卷吸經驗式不確定性研究

張維凱

浙江大學海洋學院,浙江 舟山 316000

泥沙異重流是水庫和河流入海口地區常發生的現象。當密度較大的挾沙水流遇到密度較小的水體時下潛并沿底部運動形成。科學利用異重流可以給我們的生產生活帶來很大的方便，如合理利用水庫異重流排沙可以減小水庫淤積；異重流在海洋形成的沉積區常常富含豐富的資源。國內外學者通過野外觀測、實驗和數值模擬對異重流取得了豐碩的研究成果[1-5]。特別地，異重流數值模擬由于具有很好的經濟性和時效性，越來越得到廣泛的應用。但是，異重流數學模型也存在一定的局限性，即一些物理量的計算要使用經驗關系式，如異重流層平均模型中需要引用泥沙侵蝕經驗式和水卷吸經驗式[6]。而水卷吸經驗式對異重流數學模型的計算結果影響很大，這是因為異重流與環境流體的密度差是其驅動力，卷吸水多，則異重流泥沙濃度低，反之則高，由此影響異重流與環境流體的密度差。經驗式是基于實驗數據，通過數學方法擬合得到的，存在很大的不確定性。這是因為，異重流發生在水下，難以觀測到，實驗室條件下的異重流具有較強的非恒定性，使得獲取大量高精度的野外及實測數據來率定經驗式存在很多困難[7]。

Wang和Cao提出一套基于貝葉斯定理的Metropolis-Hastings采樣法（以下簡稱概率法），能夠利用少量標準貫入實驗的數據得到大量不排水條件下楊氏模量的等效樣本[8,9]。采用這種方法的好處是可以獲得經驗系數的大量樣本，供我們分析其統計特征，對于傳統的經驗系數率定方法，得到的固定的經驗系數取值，可以預見的是，當實測數據增加或存在誤差時，經驗系數的取值將會發生變化。本文將這種方法應用于水卷吸經驗式（式1）的不確定性分析中，并將采樣系數由一個擴展為兩個，首先使用概率法獲得經驗系數的大量樣本（第一節），然后分析經驗系數樣本的統計特征。

1 水卷吸經驗式不確定性研究方法

1.1 水卷吸經驗式的介紹

Parker等提出了水卷吸經驗式[10]：

其中，ew為水卷吸系數，A=0.00153、B＝0.0204為Parker率定的經驗系數取值，Ri=Rgch/u2為理查德森數，R為有效重力，g為重力加速度，c為層平均泥沙濃度，h為厚度，u為層平均速度。

1.2 基于貝葉斯定理的Metropolis-Hastings采樣法

本文采用Metropolis-Hastings采樣法，對經驗系數N1=B/A和N2=1/A進行采樣，若假定經驗系數N1服從均值為μ1，標準差為σ1的正態分布，經驗系數N2服從均值為μ2，標準差為σ2的正態分布，那么等式2左邊服從均值為μ1+μ2Ri，標準差為的正態分布。對采樣過程敘述如下。

用Data指代實測值（即從實驗中獲得的異重流相關的Ri，ew數據），用m指代經驗系數組合，m=N1,N2），用P(m/Data)表征給定實測數據時，經驗系數某組取值的概率。根據貝葉斯定理，有[11-13]：

其中，下標j表示經驗系數樣本的序號，n為總樣本數（n=8萬），P(m)為先驗分布（即無實測數據條件下，經驗系數某組取值的概率），P(Data/m)為似然函數（即，對于給定的經驗系數取值，公式1計算值與實測值之間的擬合程度），（3）式分母為一個歸一化常量，在采樣過程中不變化，無需計算，（4）、（5）、（6）式相乘的結果即為（3）式的分子。ξi為實測的1/ew值，nS為實測值組數（55組）。μ1min、μ1max、σ1min、σ1max分別為N1先驗概率均值μ1的最小值、最大值，標準差σ1的最小值、最大值；μ2min、μ2max、σ2min、σ2max分別為N2先驗概率均值μ2的最小值、最大值，標準差σ2的最小值、最大值。

首先任意選取一組經驗系數值m0～(N1,0,N2,0)；分別以N1,0、N2,0為均值，以N1,0×σ1、N2,0×σ2為標準差，隨機取得一組新的經驗系數值樣本，記為應用式（3）-（7）式計算即的接受概率。當ra大于一個[0,1]之間的隨機數時，接受為新的起點重復上述過程，直至所得樣本取值的概率分布趨于穩定[8]。

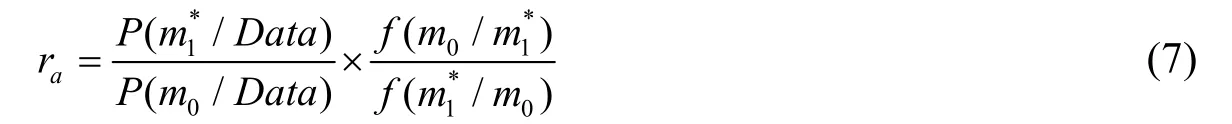
2 經驗系數的樣本分布

由于水卷吸系數應小于0.075[10]，故采樣時，給定限制條件N1≥13.3，在得到N1～N2的樣本后，通過簡單的數學計算，轉換成經驗系數A-B。考慮到A和B相差一個量級，在統計樣本的頻數分布時，首先將樣本A乘以1000，樣本B乘以100，然后以每個樣本點為圓心，0.2為半徑作圓，統計圓內點的頻數，如圖1所示。然后統計依次頻數大于2500，2490，2480……的樣本數，最終得到頻數大于22的樣本總數為76403，得到總樣本數95%的A-B樣本所在的區間范圍，使用同樣方法統計得到25%、50%、75%樣本，如圖2，其中黑色十字為概率最大樣本[A,B]＝[0.0016,0.0249]。顏色由深至淺，依次為25%、50%、75%、95%樣本的區間范圍。占總樣本95%的A-B取值組合中，A-B的區間范圍分別是概率最大A-B值的[51%,630%]和[63%,1200%]，具體范圍見表1。

表1 不同比例經驗系數樣本所在區間范圍Table 1 Interval range of different proportions of empirical coefficients

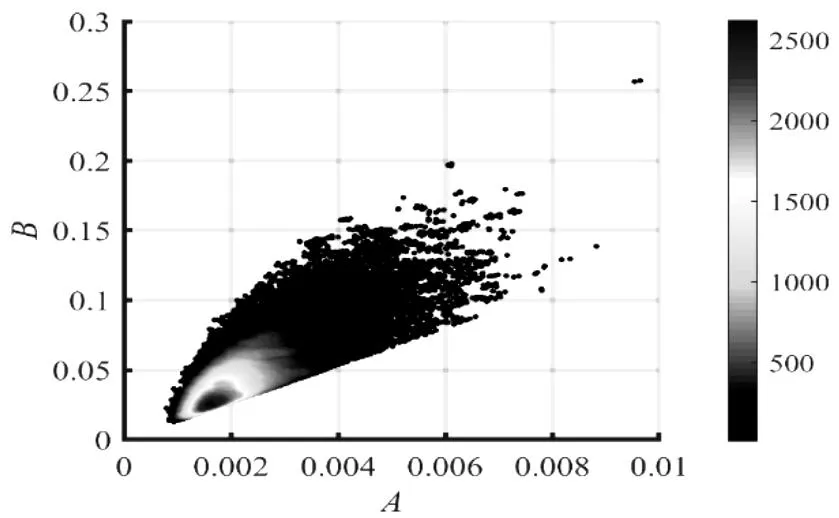
圖1 經驗系數A和B樣本分布Fig.1 Sample distribution of empirical coefficients A and B

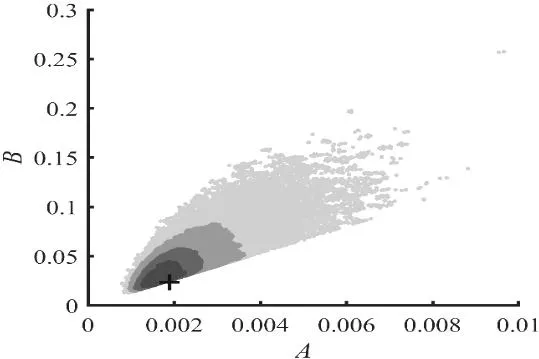
圖2 經驗系數A和B不同比例樣本所在的區間范圍Fig.2 Interval of different proportions of empirical coefficients A and B

圖3 顯示了概率最大系數組合對應的經驗式與原經驗式的對比情況，圖3a為代入概率最大系數組合的公式1與實測數據的擬合圖像，圖3b為原經驗式與實測數據的擬合圖像。可以看出，概率最大系數組合與原公式擬合結果相近。

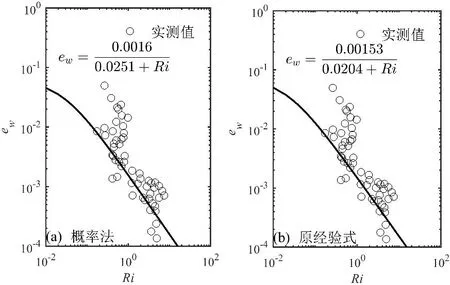
圖3 概率法擬合的經驗式與原經驗式對比Fig.3 Comparison between the empirical formula fitted by probability method and the original formula

3 結論

本文應用基于貝葉斯定理Metropolis-Hastings采樣法對異重流水卷吸經驗式進行了不確定性分析，得到了其中經驗系數組合A-B的大量樣本，并對其進行了分析，結論如下：

（1）通過概率法擬合的最大概率經驗系數組合[A,B]＝[0.0016,0.0249]與原經驗式擬合結果相近，這也說明概率法在擬合經驗式在保證傳統擬合方法的精確度基礎上，也具有更大的優勢（能夠獲得經驗系數其它取值的樣本分布，繼而得到概率密度）。

（2）95%經驗系數A-B的樣本區間范圍比25%樣本區間范圍擴大明顯（A擴大790%，B擴大832%），說明經驗系數的不確定性很大，有可能會對異重流數值模擬的結果產生較大影響。

（3）將相同比例經驗系數組合相對于最大概率系數組合的比例范圍一起比較，可以看出，經驗系數B區間范圍遠遠大于A的范圍，說明經驗系數B的不確定性更大，在率定時要尤其注意。

值得注意的是，這種基于貝葉斯定理的Metropolis-Hastings采樣法還可以應用于其它的公式，分析其中經驗系數的不確定性，且通過公式與公式之間的對比，可以判斷由于實測數據的誤差或稀少造成的經驗式不確定性的大小，當我們模擬異重流需要選取經驗公式時，可以提供一定的參考。

[1]Meiburg E,Kneller B.Turbidity currents and their deposits[J].Annual Review of Fluid Mechanics,2010,42(1)：135-156

[1]嚴忠鑾,安瑞冬,李 嘉,等.濁度型清渾水交界面識別方法及其在水庫異重流觀測中的應用[J].水利水電科技進展,2013,33(6)：71-75

[2]范家驊.渾水異重流水量摻混系數的研究[J].水利學報,2011,42(1)：19-26

[3]賀治國,林挺,趙亮,等.異重流在層結與非層結水體中沿斜坡運動的實驗研究[J].中國科學：技術科學,2016,46(6)：570

[4]趙 琴,李 嘉,安瑞冬.水庫渾水異重流的兩相流模型適用性研究[J].水動力學研究與進展,2010,25(1)：76-84

[5]胡 鵬,胡元園,賀治國,等.泥沙異重流與環境物質交換經驗式對比[J].水科學進展,2017,28(2)：257-264

[6]Wells M,Nadarajah P.The intrusion depth of density currents flowing into stratified water bodies[J].Journal of Physical Oceanography,2009,39(39)：1935-1947

[7]Wang Y,Cao Z.Probabilistic characterization of Young's modulus of soil using equivalent samples[J].Engineering Geology,2013,159：106-118

[8]曹子君,趙騰遠,王宇,等.基于貝葉斯等效樣本的土體楊氏模量的統計特征確定方法[J].防災減災工程學報,2015,35(5)：581-585

[9]Parker G,Fukushima Y,Pantin HM.Self-acceleratingturbiditycurrents[J].Journalof Fluid Mechanics,1986,171：145-181

[10]Traer MM,Hilley GE,Fildani A,etal.The sensitivity of turbidity currents to mass and momentum exchanges between these under flows and their surroundings[J].Journal of Geophysical Research Atmospheres,2012,117(F1)：1009T

[11]Hilley GE,Mynatt I,Pollard DD.Structural geometry of Raplee Ridge mono cline and thrust fault imaged using inverse Boundary Element Modeling and ALSM data[J].Journal of Structural Geology,2010,32(1)：45-58

[12]Ang AHS,Tang WH.Probability concepts in engineering：emphasis on applications to civil and environmental Engineering[M].Beijing：China Architecture&Building Press,2017