粒子群優化PID在變風量空調系統中的應用

王長濤，郭高超,趙劍明,韓忠華,,3,朱　毅

(1.沈陽建筑大學信息與控制工程學院,遼寧 沈陽 110168;2.中國科學院沈陽自動化研究所,遼寧 沈陽 110016;3.中國科學院網絡化控制系統重點實驗室,遼寧 沈陽 110016)

0　引言

變風量(variable air volume,VAV)空調系統以其節能和操作相對簡便的優點，越來越受到人們的重視。目前，空調系統一般都是采用常規的比例-積分-微分(proportion integration differentiation，PID)調節控制器。在特定工況下，傳統的PID控制方式能夠得到較好的效果。但對于變風量空調系統來說，系統在運行時會因自身的一些因素，導致控制性能受到限制。特別是當系統啟動或工況切換時，控制系統很容易出現滯后。目前所使用的控制方式很難達到使用要求[1]。本文提出利用群體智能算法對PID進行整定。

隨著智能算法在控制方面的發展，越來越多的智能控制優化算法被用于PID參數整定。常見的控制參數整定方法有神經網絡算法、Ziegler-Nichois(Z-N)算法、遺傳算法等[2]。與這些算法相比，粒子群算法的優勢就是設定參數少、整體尋優能力強。本文針對變風量空調系統自身的時滯性、非線性、非平穩性以及不確定性等變化特性，采用粒子群算法，對控制器的不足之處進行優化[3]。

1　PID控制器概述

在變風量空調系統中,PID控制對受控對象(即房間溫度數學模型)的準確度要求并不高。PID控制系統結構如圖1所示。

圖1　PID控制系統結構圖

相對應的PID控制器函數表達式為：

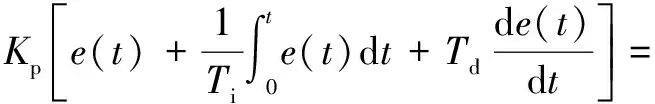
(1)

式中：e(t)為設定值與反饋值的差，即系統誤差；Ti為積分時間的常數；Td為微分時間的常數；Kp為系統誤差信號的比例量權值；Ki為系統誤差信號的積分量權值；Kd為系統誤差信號的微分量權值。

通過Kp、Ki、Kd三個權值，PID控制器能得出控制對象的信息，從而對受控的對象進行驅動。所以，PID在系統中的應用效果主要取決于Kp、Ki、Kd在系統的組合值。對于VAV空調這種非線性系統來說，需要對系統中的PID的參數選取一組合適的組合值，以達到預期的控制效果[4]。

2　改進粒子群優化算法

1995年，Kennedy和Eberhart提出的粒子群優化 (particle swarm optimization,PSO)算法是計算智能領域的一種計劃計算技術[5]。首先設置一個D維空間,其大小是由n個粒子組成的種群x=(x1,x2,…,xn)。在這個D維的搜尋空間里，每個粒子都具有一定的飛行速度。空間中的粒子都可用相對應的向量來體現，而這個向量也是隱藏的最優解。通過目標函數，可對每個粒子所在位置xi進行適應度值計算。第i個粒子的速度為vi=(vi1,vi2,…,viD)T，其個體極值為Pi=(Pi1,Pi2,…,PiD)T,種群中粒子的尋優極值Pg=(Pg1,Pg2,…,PgD)T。粒子群被初始化為一組隨機的粒子，經過迭代來更新位置和速度。

更新方程式如式(2)和式(3)。

(2)

(3)

式中：xid為粒子的位置；vid為粒子的速度；c1和c2為粒子增速的常數；r1和r2為均勻分布的隨機常數，取值范圍為[0,1],其主要作用是增加粒子飛行時的隨機性，通常都是通過比較最后的效果來固定取值。

基本粒子群更新過程如圖2所示。圖2中：Pbestid(t)為粒子目前所處較佳位置；gbestid(t)為粒子在整個粒子群中目前所處較佳位置。

圖2　基本粒子群更新過程示意圖

為了提高基本粒子群算法避免陷入局部極值的能力[6]，引入了慣性權重的概念[7]。PSO具有的最大全局搜索能力主要取決于vmax的取值。當vmax的值很小時，會影響粒子在全局中的搜索能力，慣性權重的作用也體現不出，粒子群只能限制于局部搜索。相反，當vmax的值很大時，可以通過找到適當的ω值來調節粒子群，從而擴大粒子搜索范圍并提升全局搜索能力。因此，只需要一個恰當的ω值，粒子既能實現局部搜索，也能實現全局搜索[8]。其速度更新公式為：

(4)

式中：ω為一個非負數。

當ω為0時，即基本粒子群算法。ω作為約束粒子速度的慣性權重，約束后的粒子更新方式與基本粒子群粒子的速度更新方式相同。2001年，Y.Shi研究發現，當ω較小時,粒子群算法近似于局部搜索算法，即具有很強的局部開發能力，能夠以很快的收斂速度找到全局最優解。相反，當ω較大時，粒子群具有很強的全局搜索能力，但其收斂速度較慢且失敗的概率較大。為此，不少學者通過在算法進化過程中自適應地改變慣性權重系數，以滿足算法進化的需要。所以，本文中的慣性權重不是一個定值，而是隨時間線性減小的函數。

3　PSO算法優化PID參數

對PID控制器參數的優化問題，都是尋找更合適的三個參數：比例、積分和微分系數，即Kp、Ki、Kd，使最后系統的性能指標更好。本文采用PSO算法對PID的參數進行整定。PSO算法優化PID參數的原理圖如圖3所示。

圖3　PID參數優化原理圖

如圖3所示，本文在Matlab軟件上進行PSO算法優化PID控制器的研究，并在Simulink環境中建立PID控制流程模型圖，最后通過編輯程序來實現粒子群算法的優化。PID控制器的系統模型和PSO算法程序的連接介質是粒子，其表示的是PID控制器參數及其相對應的適應度值。本文采用誤差絕對值乘時間積分(integrated time absolute error,ITAE)的性能評價指標作為粒子群優化中的適應度函數，其函數形式為：

(5)

目前，從硬件上來說，PID控制器操作簡單，易于在計算機上實現；從原理上來說，優化后的參數使系統具有良好的穩定性以及較快的響應時間；從描述系統的誤差范圍來說，有很多性能指標，如誤差平方積分(integrated square error,ISE)、誤差絕對值積分(integrated absolute error,IAE)、ITAE等。本文采用ITAE指標，即算法的適應度函數。

3.1　PSO算法調整PID參數

PSO算法調整PID參數的步驟如下。

①粒子群初始化。其中包含參數設置并產生粒子群。隨機產生一組粒子，數量為N，維數為3。最大迭代次數為100。粒子搜索目標空間范圍為：

xi(t)∈[xmin,xmax]

xmax=[Kpmax,Kimax,Kdmax]

xmin=[Kpmin,Kimin,Kdmin]

速度范圍為：

Vi(t)∈[vmin,vmax]

粒子群算法如下：

(6)

(7)

則xi(t)=swarmi(t)=[Kpi,Kii,Kdi]。

②對當前第t代粒子群的適應度函數值進行計算。

Ji(t)=J[xi(t)]

式中：i=1,2,…,N;t=1,2,…,100。

此時的目標函數是對粒子群中每個粒子適應度值的評估。

③將當前得出的適應度值與種群中每個粒子的當前最佳位置作比較。

如果Ji(t)>JPbesti(t)，則JPbesti(t)=Ji(t),Pbesti(t)=swarmi(t)。

④將當前得出的適應度值與種群中每個粒子的歷史全局最佳位置作比較。

如果Ji(t)>Jgbesti(t)，則Jgbesti(t)=Ji(t),gbesti(t)=swarm(i)。

⑤粒子的位置和速度根據式(3)和式(4)進行調整。慣性權重的函數形式為：

(8)

式中：ωmax和ωmin為慣性權重的最值，ωmax=0.9、ωmin=0.4。

⑥粒子速度的約束條件為：

(9)

式中：i=1,2,…,N;t=1,2,…,100。

⑦粒子搜尋約束條件為：

(10)

式中：i=1,2,…,N;t=1,2,…,100。

⑧PSO算法優化PID參數流程如圖4所示。

圖4　PID參數優化流程圖

圖4中，迭代終止的條件是：選擇最大迭代次數或粒子群搜索到的最佳值，并達到了設定的最小值(即閾值)。

3.2　試驗與仿真研究

變風量空調系統控制的主要對象是室內溫度。室內溫度受外界因素、室內散熱電器、人流量等多種因素變化的影響。故變風量空調系統是一個摻雜多種因素的熱力學系統。因此，難以建立精確的空調房間數學模型[9]。本設計在不考慮其他因素時，假定房間的溫度是均勻分布的。通過查閱相關的文獻資料，確定空調房間模型的傳遞函數為：

(11)

對目標函數的最大值進行變換時，粒子對應的系數為函數的最佳值。粒子群算法以代碼形式創建Matlab.m文件，參數的設置是通過粒子在空間中搜尋得到的。首先，需要對粒子群程序中的參數以及Simulink環境中的模塊進行設置；然后，設置程序中種群的粒子總數N。種群的數量與計算機CPU的消耗情況成正比；目標函數的平均最優解并非呈線性增長，而是先減小再增大。較大或較小的種群量都會降低算法在搜索中的隨機概率，減少平均迭代的次數。根據本次種群的數量N=100,本文設置最大的迭代次數為100。慣性權重隨著粒子迭代從ωmax=0.9遞減到ωmin=0.3。經過多次試驗對比，當ω=0.6時，分析平均最優解、平均迭代次數和平均消耗CPU的時間等參數，全局最優率最高。選取學習因子，即加速常數c1、c2。當c1和c2的組合比較適當時，其目標函數的平均最優解較高，優化效果良好。調節c1、c2的不同組合即調節解的離散程度，以控制算法的探索和開發[10]。通過幾組數據的比較，得到當c1=c2=2時，全局最優率較高。以系統誤差e(t)為輸入，以3個算法優化參數為輸出，創建了功能塊編程形式的空調系統。

這里要強調的是：針對變風量空調房間溫度的調節控制問題，若以某個參數固定值進行算法優化，必然無法達到預期效果。所以，在參數取值時，只有通過折中的方式兼顧。

PSO_PID控制系統模型如圖5所示。

圖5　PSO_PID控制系統模型

在Matlab程序實現的過程中，需要一部分程序實現智能算法與Simulink環境下PID模型之間的參數傳遞。PID模型參數傳遞程序如表1所示。

表1　PID模型參數傳遞程序

在粒子值向PID模型傳遞參數的過程中，x為粒子群算法傳遞來的空間粒子。首先，利用調用函數assignin,分別將x(1)、x(2)、x(3)賦值給工作區Workspace中的PID參數Kp、Ki、Kd，以實現智能算法程序向PID模型的參數傳遞。然后，利用調用函數sim，實現對Simulink環境中PID控制系統的階躍響應仿真。PID_model是Simulink環境中PID控制系統的文件名，設定的運行時長為[0,120]，控制系統模型輸出端子out1的值為返回的y_out。最后，實現ITAE性能指標向x(1)、x(2)、x(3)的復制。

4　仿真結果分析

為了驗證改善后的PID控制器對房間溫度的控制效果[11]，分別采用基本粒子群算法和Z-N算法對PID進行整定。仿真優化曲線如圖6所示。

圖6　仿真優化曲線

根據圖6，加權后粒子群算法整定得到參數Kp=300,Ki=0.067,Kd=106.54。優化后的ITAE變化曲線如圖7所示，ITAE=0.405。

圖7　優化后的ITAE變化曲線

通過使用Z-N算法、基本粒子群算法和加權后的粒子群算法來優化PID控制器的參數，并將優化結果運用到變風量空調溫度控制系統中，得到VAV系統在不同算法下階躍響應對比圖，如圖8所示。

圖8　階躍響應對比圖

通過圖7中的變化曲線能夠看出，優化程序在運行的過程中，適應度值越來越小，直到穩定在一個固定值，表明粒子在不斷地尋找較好的參數值。由圖8可以看出，本次設置滯后的時間為12 s，每一種控制方式都有不同振蕩情況的跳躍。Z-N算法整定之后的PID控制收斂速度比較緩慢，上升的時間相對較快，但是系統調節的時間較長，同時超調量也相對較大。這對于空調房間溫度的控制沒有達到很好的效果，滯后時間較長，不利于在空調工況切換時使用。引入基本粒子群算法后，PID控制的速度明顯加快，振蕩有所改善，系統調節時間和變化幅度較短，滯后時間縮短了大約3 s。使用粒子群算法對PID控制器的參數賦值運算后，幾乎消除了超調量，并明顯縮短了上升時間。通過以上分析可知，本文使用的優化算法適用于空調系統，對房間溫度滯后問題的優化效果明顯，提高了系統的控制性能。

5　結束語

本文針對具有二階慣性、純滯后特點的被控對象(即變風量空調系統)，采用粒子群智能算法的優化策略，對PID控制器各參數進行優化；同時,采用基本粒子群算法以及Z-N算法進行整定，并對結果進行比較。從三種算法對PID參數整定的仿真結果可看出，加權后的粒子群算法實現了對變風量空調這種非線性系統的實時溫度控制。

通過分析變風量空調溫度系統在應用中的不足，提出了一種基于改進粒子群算法優化PID參數的方法。這種優化方法應用到具有多種變化特性的變風量空調系統中，提高了系統的控制性能。

參考文獻:

[1] ZHAO Z,YU N.The application of advanced control technologies in air conditioning system-a review[J].Advance in Building Energy Research,2017,11(1):52-66.

[2] SAHU R K,PANDA S,ROUT U K,et al.Teaching learning based optimization algorithm for automatic generation control of power system using 2-DOF PID controller[J].International Journal of Electrical Power & Energy Systems,2016,77(1):287-301.

[3] FREIRE H,OLIVEIRA P B M,PIRES E J S.From single to many-objective PID controller design using particle swarm optimization[J].International Journal of Control,Automation and Systems,2017,15(2):918-932.

[4] 蔡超,周武能.人工蜂群算法整定PID控制器參數[J].自動化儀表,2015,36(8):74-77.

[5] 王華國,孫玉坤,王博,等.改進的PSO-FNN在發酵軟測量中的應用[J].自動化儀表,2016,37(3):62-64.

[6] WANG G G,HOSSEIN G A,YANG X S,et al.A novel improved accelerated particle swarm optimization algorithm for global numerical optimization[J].Engineering Computations,2014,31(7):1198-1220.

[7] 楊智,陳穎.改進粒子群算法及其在PID整定中的應用[J].控制工程,2016,23(2):161-166.

[8] SUN W,XU Y.Using a back propagation neural network based on improved particle swarm optimization to study the influential factors of carbon dioxide emissions in Hebei Province,China[J].Journal of Cleaner Production,2016,112(2):1282-1291.

[9] ZHU Y,JIN X,DU Z,et al.Simulation of variable refrigerant flow air conditioning system in heating mode combined with outdoor air processing unit[J].Energy and Building,2014,68(s1-2);571-579.

[10]ZHANG H,HU J,BU W.Research on fuzzy immune self-adaptive PID algorithm based on new smith predictor for networked control system[J].Mathematical Problems in Engineering,2015(10):1-6.

[11]呂磊,章國寶,黃永明.基于蝙蝠算法的PID參數整定[J].控制工程,2017,24(3):548-553.