基于蟻群算法的六自由度并聯平臺控制參數優化

周　亮，馬訓鳴

(西安工程大學機電工程學院，陜西 西安 710048)

0　引言

Stewart平臺具有結構簡單、剛度大、承載能力強、運動負荷小以及積累誤差小等優勢[1]。Stewart平臺由六套閥控缸電液位置伺服系統組成，而液壓缸系統的連接將影響其相互間各通道的輸出和控制，導致系統控制精度的下降以及負載的交聯耦合。一般而言，為了提高整個系統的控制精度，主要采用提高單通道抗干擾性和控制精度的方法。而非線性時變的單通道電液位置伺服系統具有參數變化大、阻尼比小、非線性程度高等特點[2]。比如通過采用閉環比例控制系統,利用該系統的振蕩周期和臨界比例增益獲得PID控制器的3個參數值，即常規的PID控制參數整定方法(Z-N法)[3]。因為該方法并未獲得伺服控制參數的最優值，所以易使系統產生超調現象。Charles C[4]為了改進傳統自適應方法在計算逆動力學模型方面的不足，提出了一種非補償模型參考自適應控制方法。但由于該方法必須以平臺的緩慢運動變化作為前提條件，故不適用于運動變化較快的平臺。呂彬[5]提出了通過遺傳算法調節PID控制器參數的方法，但搜索較精確的解需要較多的時間。由于參數的選擇決定解的優化與否，且遺傳算法參數選擇大部分取決于經驗，故參數的選擇經驗顯得尤為重要。此外，還有一些學者為了最優化某種性能指標，通過神經網絡調節PID控制器的參數。

1　基于蟻群算法的PID控制系統設計

1.1　PID控制器參數優化原理

在PID控制系統中，與PID位置算式[6]對應的PID增量算式為：

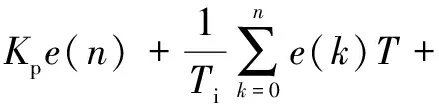
(1)

式中：Δu(n)為本次控制量的增量；e(n)為本次控制偏差；Kp為比例系數；Ti為積分時間常數；Td為微分時間常數；T為采樣周期。

在式(1)中，假設被控對象的模型和采樣周期已知，只要Kp、Ti和Td這3個參數確定，PID控制器就可以使控制系統的某個性能指標達到最優。

工業控制過程中，使用較普遍的策略是PID控制。PID控制具有魯棒性好、算法簡單、可靠性高等優點。蟻群算法由于具有正反饋、分布式、自組織等優點，是一種魯棒性較強的仿生進化算法[7]。因此，本文采用基于蟻群算法的PID控制器對Stewart平臺非線性模型進行控制，有效地避免了常規PID控制算法的局限性，改善了其性能。蟻群算法的PID參數優化系統框圖如圖1所示。

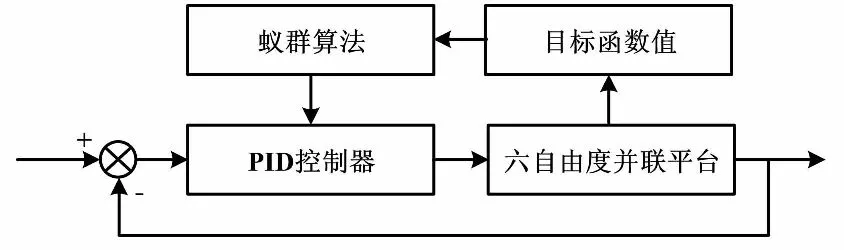
圖1　PID參數優化系統框圖

1.2　蟻群算法設計

①構建爬行路徑。

段海濱[8]對螞蟻爬行路徑進行設計改造。按規則：Kp有6個有效數位，即小數點前2位、小數點后4位；Ti和Td都有5個有效數位，分別為小數點前1位、小數點后4位。把這3個參數抽象地表示在xoy平面上，作為螞蟻節點和爬行路徑，如圖2所示。假設有16條垂直于x軸的等長度且等間距的線段：L1，L2,…，L16。圖2中的橫坐標為L1～L16在x軸上的位置，分別代表Kp、Ti和Td的數位。然后，對線段進行9等分，則各個線段都會有10個節點，表示每個節點在各個線段上可能取10個值，分別為0～9。如節點(3，7)表示Kp的第3個數位(即Kp值小數點后第1位)值為7。

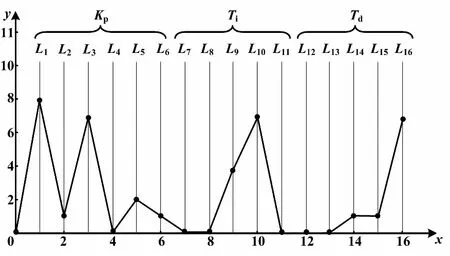
圖2　螞蟻節點和爬行路徑

在蟻群的爬行路徑中， PID控制器參數和各個節點構成映射關系，3個參數的計算公式為：

(2)

圖2中，螞蟻的爬行路徑為(8-1-7-0-2-1-0-0-4-7-0-0-0-1-1-8)。按照式(2)，可表示一組PID控制器參數為(81.702 1，0.047 0，0.011 8)。

②建立目標函數。

目標函數需保證系統具備良好性能，因此必須以系統的性能指標為依據。采用單一的目標函數作為傳統的工程優化指標，很難使伺服控制系統的動態性能達到最佳狀態。為了得到更好的動態性能，可定義目標函數為：

(3)

式中：σ為超調量；tr為上升時間；ts為調整時間；σ0、tr0和ts0為采用傳統Z-N法[3]得到的系統性能指標；λα、λtr和λts為加權系數，λσ+λtr+λts=1。根據經驗，λσ、λtr和λts分別取為0.6、0.2和0.2。

σ、tr和ts的約束條件為:

(4)

③路徑點的選擇。

蟻群根據基準路徑，按照每個節點的信息量(即轉移概率)，依次選擇所有節點并生成蟻群路徑。每個節點的信息量決定蟻群轉移概率，而蟻群爬行路徑又是根據基準路徑上每個節點的信息量的變化而變化的。若所有螞蟻都是從坐標原點出發，經節點(xi,yi)爬行到下一個節點(xi+1,yj+1)，則按照隨機規則選擇路徑。若設Pk(xi,yi,j,t)為該時刻第k只螞蟻爬行的概率，則：

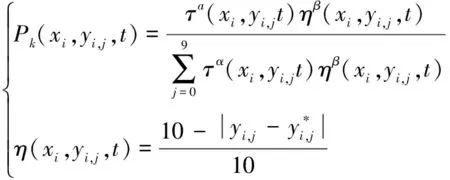
(5)

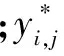
④信息素的更新。

啟發信息會因為殘留信息過多而被吞沒。為了防止該狀況的發生，在蟻群實現一次循環后，需要更新各個節點的殘留信息。

因此，在(t+n)時刻，路徑(i,j)上的信息量可按以下規則進行調整：

(6)

式中：ρ為信息素揮發系數；Δτij(t)為此次循環中路徑(i,j)上的信息素增量，初始時刻Δτij(0)=0；m為蟻群的規模。

(7)

式中：Q為信息素強度；Jk為目標函數值。

對信息素揮發系數ρ采用自適應控制策略，可以提高求解的效率，即將該系數變成如下閾值函數：

(8)

式中：ρmin為最小信息素揮發系數。

通過上述分析，得到基于蟻群算法的六自由度PID控制參數最優解算法流程圖，如圖3所示。

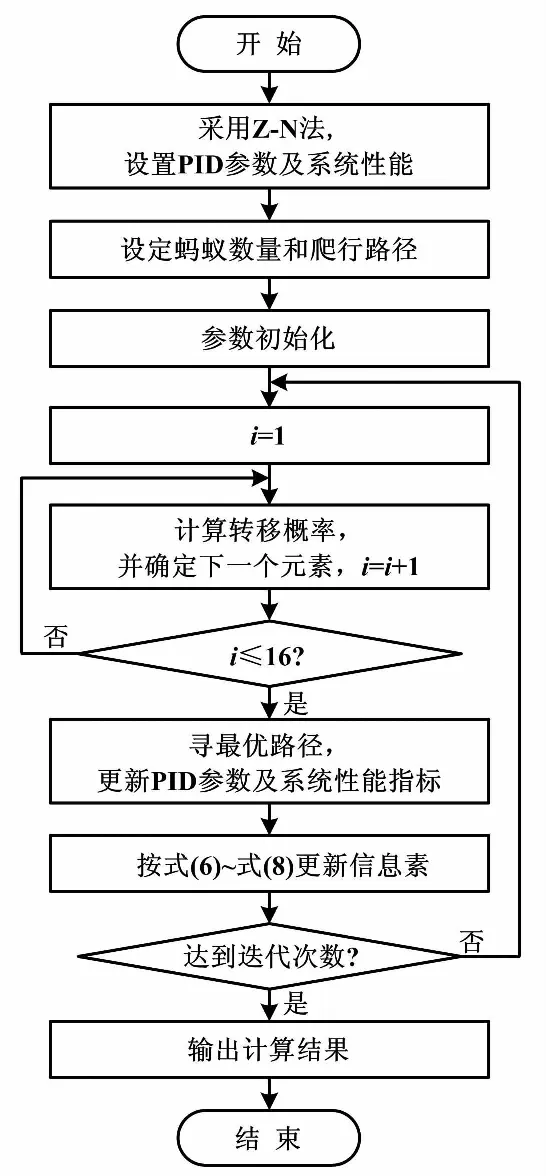
圖3　算法流程圖

2　系統的數學模型及仿真

因為Stewart平臺的6個液壓伺服通道是相同的，如果要為控制器設計提供依據，則只需要對單通道進行傳遞函數推導。Stewart平臺單通道伺服系統的廣義被控對象為功率放大器、比例閥、液壓缸及其負載。被控對象結構如圖4所示。

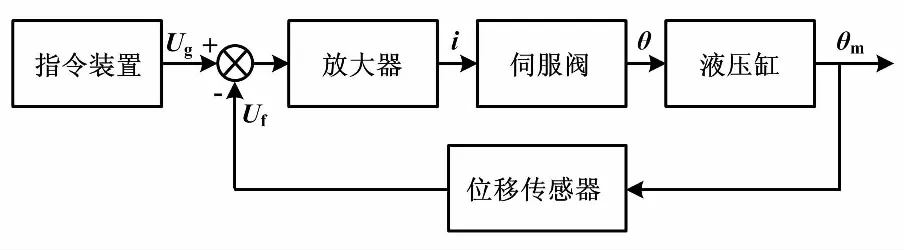
圖4　被控對象結構圖

以下討論各個環節的傳遞函數[9]。

①放大器傳遞函數的確定。

本伺服系統采用電流負反饋型伺服放大器。由于其動態特性可以忽略不計，故輸入電壓Ug和輸出電流ΔI近似成比例，其增益Ka為：

(9)

②位移傳感器傳遞函數的確定。

循環式真空噴砂系統使用負壓系統進行砂粒的回收工作，系統所需負壓由真空源提供，常用的真空源種類有高壓離心風機、羅茨風機、真空泵和氣動真空發生器等[7].用于金屬砂粒回收的壓力必須達到30～60 kPa，且應具有足夠的空氣流量.常見的高壓離心風機，壓力較高，但空氣流量較低，回收能力較弱，適于磨料的短距離回收或小密度、小顆粒噴砂介質的回收，如塑料砂粒和植物型砂粒等.羅茨風機能夠提供所需的較高壓力，但工作噪聲較大.真空泵雖可以達到較高壓力，但常用的真空泵流量都比較小，不適用于大量砂粒的回收.氣動真空發生器，氣體流量很小，也不適用砂粒的回收.

本伺服系統采用的是MTS公司的磁致伸縮傳感器，其動態特性可以忽略不計，傳遞函數也可以作為比例環節處理。其傳遞函數為：

(10)

③伺服閥傳遞函數的確定。

系統采用的是HVM064型比例換向閥，其傳遞函數為：

(11)

式中：Q0為伺服閥的空載流量；ΔI為伺服閥的工作電流；Ksv為伺服閥的流量增益；ζsv為伺服閥的阻尼比；ωsv為伺服閥的固有頻率。

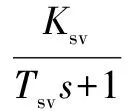
④液壓缸傳遞函數的確定。

由于負載特性沒有彈性負載，故液壓馬達和負載的傳遞函數為：

(12)

式中：θm為伺服油缸輸出量；θ0為伺服油缸輸入量；Ap為伺服油缸的內徑面積；ζh為阻尼系數；ωh為液壓缸的固有頻率。

通過上述分析，可得到六自由度平臺的單通道伺服系統框圖，如圖5所示。

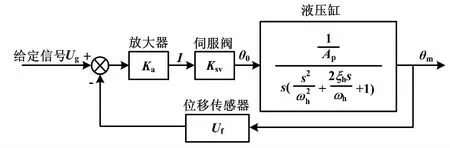
圖5　單通道伺服系統框圖

忽略干擾的影響，由圖5可得系統的開環傳遞函數為：

(13)

式中：qn為伺服閥的額定流量；ps為實際供油壓力；In為伺服閥的額定電流；psn為通過額定流量時伺服閥的壓降；Vt為油缸兩腔的總控制容積；Mt為轉動慣量；βe為液壓油的有效體積的彈性模量。

液壓伺服系統參數值如表1所示。

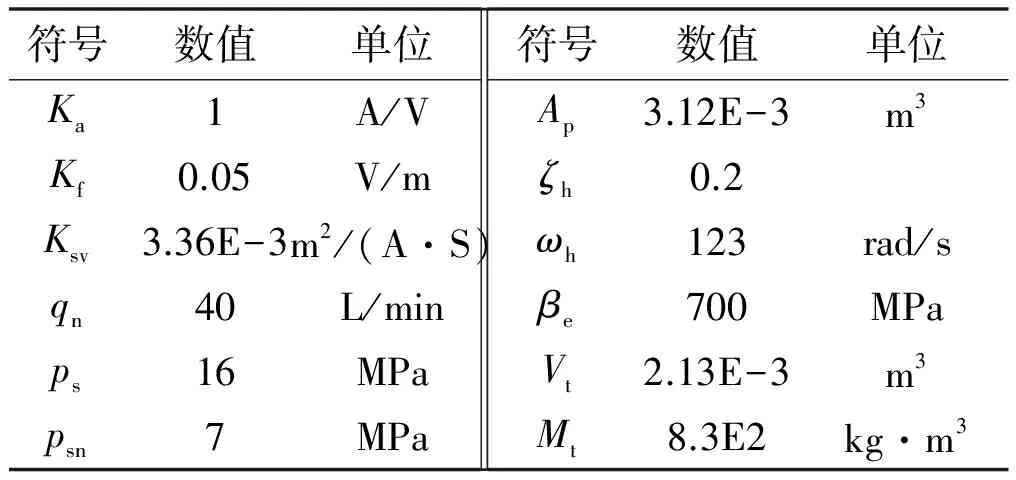
表1　液壓伺服系統參數

蟻群算法的主要初始化參數如表2所示。

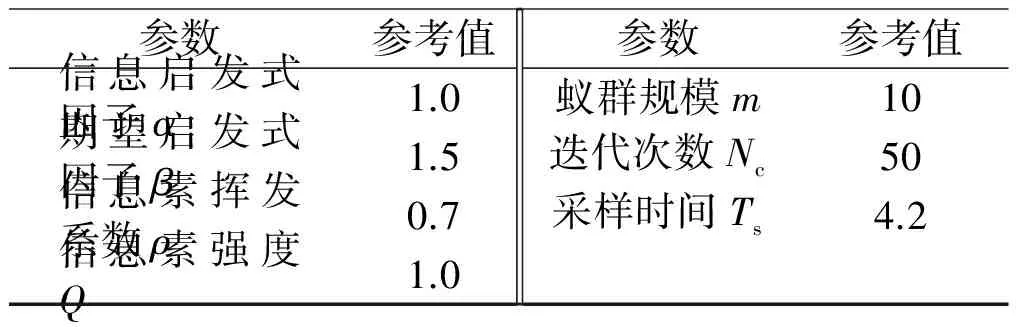
表2　主要初始化參數

通過Matlab軟件，利用蟻群算法，對Z-N法求出的PID控制參數進行仿真。PID 控制器蟻群設計的系統的階躍響應曲線如圖6所示。

由圖6可以看出，采用Z-N法系統的超調量為68.01%；而采用改進的蟻群算法，超調量僅為16.97%，系統的動態性能得到了顯著的改善。

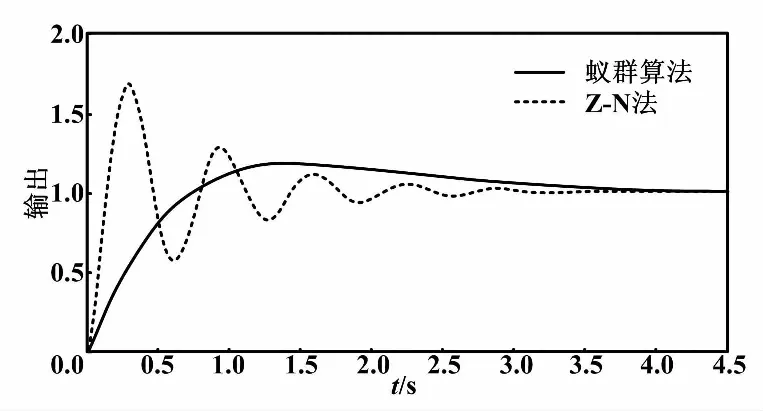
圖6　階躍響應曲線

蟻群算法的最優值進化曲線如圖7所示。

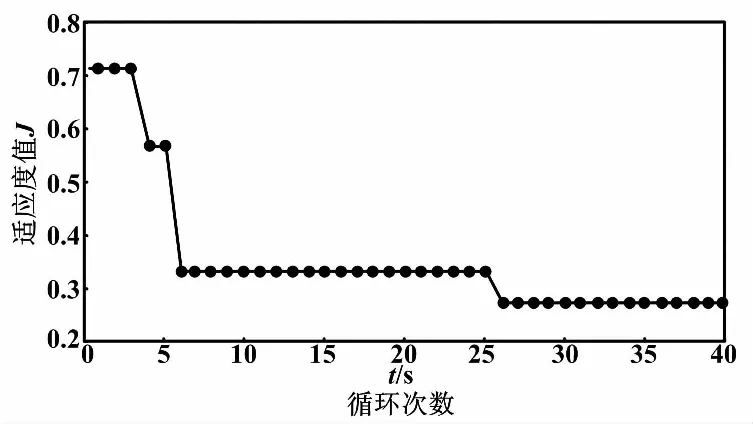
圖7　最優值進化曲線

Z-N法和蟻群算法的PID參數和性能指標如表3所示。

表3　PID參數和性能指標

3　結束語

基于六自由度并聯平臺的 PID控制參數優化問題，提出了蟻群 PID優化算法。該優化算法能夠提高響應速度，有效減少伺服系統的超調。同時，本文提出了一個具有不完全微分的最優PID控制器設計方法。該方法具有一定的有效性及應用價值，可在理論和實踐方面作進一步的探索。由于該優化策略不依賴被控對象的確定數學模型，解決問題更便利，適應性更強，因此可以應用于其他平臺控制參數的優化問題。算法的參數需要根據經驗設定。設定的參數不同，優化的效果也不同，從而在一定程度上限制了蟻群算法的應用。

參考文獻:

[1] 汪勁松,黃田.并聯機床-機床行業面臨的機遇與挑戰[J].中國機械工程,1999,10(10):60-65.

[2] 李磊.六自由度并聯平臺運動規律及控制方法研究[D].哈爾濱:哈爾濱工程大學,2007.

[3] ZIEGLER J G,NICHOLS N B.Optimum settings for automatic controllers[J].Transactions of the A.S.M.E.,1942,64(11):759-765.

[4] NGUYEN C C,ANTRAZI S S,ZHOU Z L.Adaptive control of a Stewart platform-based manipulator[J].Journal of Robotic Systems,1993,10(5):657-687.

[5] 呂彬,董建園.基于遺傳算法的六自由度并聯平臺的控制[J].計算機工程與應用,2015,51(2):76-81.

[6] 陶永華,尹怡欣,葛蘆生.新型PID控制及其應用[M].北京:機械工業出版社,1998.

[7] 詹士昌,吳俊.基于蟻群算法的 PID 參數優化設計[J].測控技術,2004,23(1):69-71.

[8] 段海濱.蟻群算法及其應用[M].北京:科學出版社,2005.

[9] 周亞超.并聯式六自由度液壓運動平臺的分析與研究[D].合肥:合肥工業大學出版社，2015.