發酵罐KPCA與SVR軟測量技術的研究

李浩光,于云華，沈學峰,黃　磊

(1.中國石油大學勝利學院，山東 東營 257061；2.中國石油大學(華東)信息與控制工程學院，山東 東營 257061)

0　引言

青霉素發酵過程具有較強的非線性、時變性和不確定性，發酵過程中的基質濃度等關鍵生物參數因缺乏專用傳感器，難以實現實時在線測量[1-4]。

針對生物發酵過程的復雜性、多樣性，以及發酵過程中各過程變量與重要輸出變量之間存在的非線性關系[5-9]，提出了一種基于核主成分分析-支持向量機回歸(kernel principal component analysis-support vector regression,KPCA-SVR)的非線性回歸軟測量方法。該方法采用核函數為高斯核函數(Gaussian kernel function，GKF)的核主成分分析(kernel principal components analysis,KPCA)法，將數據映射到高維空間中，并對映射后的數據作非線性特征提取；再利用支持向量機回歸(support vector regression,SVR)法建立軟測量模型，對菌體濃度、基質濃度和產物濃度等變量進行預測。試驗結果表明，與常規方法比較，基于KPCA-SVR的軟測量模型能夠更好地跟蹤真值的變化趨勢，且具有更高的預測精度，可以實現青霉素反應過程中關鍵變量的實時在線測量。

1　KPCA特征提取算法的原理

主成分分析(principal components analysis，PCA)是一種無監督線性特征提取方法，常用于高維數據的降維。而KPCA是一種無監督非線性特征提取方法。KPCA將核映射方法引入主成分分析，能夠有效處理非線性數據；通過非線性函數變換，將獲取的數據映射到高維特征空間中進行處理，以捕捉原始數據的非線性分布特性[10-12]。生物發酵過程中獲取的輔助變量與輸出變量也存在非線性的關系，采用KPCA方法可以構建適用于發酵過程的回歸預測模型。

若原始空間為Rn，輸入數據X有m個樣本，其中各樣本為n維，則X=[x1,x2,…,xm],xi=[xi1,xi2,…,xin],i=1,2,…,m。定義H為高維特征空間(Hilbert泛函空間)，假設映射Φ：Rn→H,則對任意xi∈Rn，可以通過非線性變換Φ將其投影至高維空間：

xi→Φ(xi)

(1)

定義核函數:

K=Φ(X)TΦ(X)=[k(xi,xj)]m×m

(2)

式(2)中:

k(xi,xj)=〈Φ(xi)T,Φ(xj)〉=Φ(xi)TΦ(xj)

(3)

將非線性函數Φ投影至H空間，求得協方差矩陣：

(4)

設協方差矩陣C的特征值為λ、特征向量為V，則：

λV=CV

(5)

存在由特征向量V={Φ(x1)，Φ(x2)，…,Φ(xm)}構成的子空間，則必然存在α={α1，α2，…,αm}，并滿足：

(6)

對式(5)作如下變換：

λ[Φ(xk)×V]=Φ(xk)CVk= 1,2，…，m

(7)

根據式(4)、式(6)、式(7)，可得：

(8)

再將式(8)整理后得到：

(9)

將式(2)、式(3)代入式(9)，化簡可得:

mλα=Kα

(10)

由此可解出特征值λ和關于K矩陣的特征向量α。

在計算協方差矩陣前，首先需要進行數據中心化處理。因此，在上述計算中，K需要經過中心化才能進行下一步計算，即計算特征向量和特征矩陣。經過數據中心化之后的K矩陣變為：

(11)

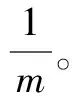
核函數需要滿足Mercer條件。常見的核函數如下。

①線性核函數：K(x,y)=xTy+1。

②多項式核函數：K(x,y)=(xTy+1)p。

④sigmoid核函數:K(x,y)=tanh(axy+c)。

2　支持向量機回歸的原理

SVR是基于統計學習理論發展而來的一種方法，在涉及小樣本數、非線性和高維數據空間的問題時具有一定的優勢。該方法通過升維，在高維空間中構造線性決策函數。為適應訓練樣本集的非線性，傳統的擬合方式一般是在線性方程中加入高階項。但該方法存在過擬合的問題。SVR算法采用核函數的方法可以避免這一問題。因此，使用核函數代替線性方程中的線性項，可以實現算法“非線性化”，進而實現非線性回歸[13-15]。

對于分類問題，支持向量機相當于標記樣本為有限集。支持向量機回歸的問題就是標記集合為不可數。其訓練集表示如下：

S={(x1,y1),(x2,y2),…,(xi,yi)|xi∈Rn,yi∈R}

SVR可分為線性SVR和非線性SVR兩種。

(1)線性SVR：對于給定的樣本集S及?ε>0,若空間Rn中超平面f(x)=+b(w∈Rn,b∈R)滿足|yi-f(xi)|≤ε、?(xi,yi)∈S，則稱f(x)=+b是樣本集合S的ε-線性回歸。

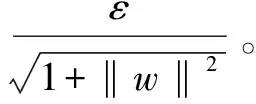
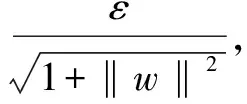
ε-線性回歸問題等價于以下優化問題：

(12)

引入松弛變量，并使用Lagrange 乘子法，得到式(12)的對偶形式：

(13)

(2)非線性SVR：對于空間Rn中線性不可分樣本集S，使用非線性函數φ將S變換至高維特征空間，并在該高維特征空間中進行線性回歸，再變換至原始空間Rn中。其對偶優化如式(14)：

(14)

非線性SVR實現方法如下。

①尋找一個核函數K(s,t)，使得K(xi,xj)=<φ(xi),φ(xj)>。

(15)

③計算b：

(16)

④構造非線性函數：

(17)

3　軟測量模型的建立

3.1　試驗數據的獲取

根據青霉素發酵機理以及生產經驗，選取時間、溫度、反應熱量、通氣量、攪拌速度、發酵罐壓力、溶氧量值、反應器體積、熱水流速、冷水流速、CO2濃度、葡萄糖添加率、基質添加率作為模型的輸入量，基質濃度、菌體濃度、青霉素濃度作為模型的輸出量。試驗共采集了15個發酵批次的數據，采樣間隔時間為4 h，獲得3個離線輸出參量(產物濃度、菌體濃度、基質濃度) 。本文將發酵生產過程中離線化驗的測量值作為預測模型的輸出真值。為保證模型包含足夠多的數據量，通過多項式插值法得到每隔15 min的在線檢測數據，建立青霉素發酵數據庫。青霉素發酵試驗單個批次的發酵時間大約為180～200 h。由于采集到的樣本數據來自于不同的批次，為便于建立數學模型，應首先對樣本數據進行歸一化預處理[11]。

3.2　模型建立

青霉素發酵過程采用基于KPCA特征提取的SVR分析，軟測量模型如圖1所示。

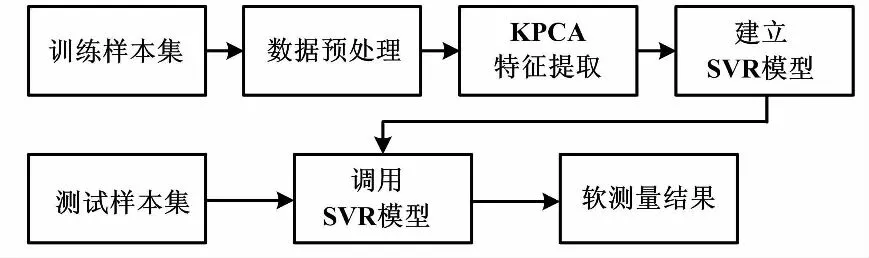
圖1　軟測量模型

首先，選取訓練樣本集，進行歸一化預處理。選取KPCA的核參數，對歸一化預處理后的數據KPCA進行特征提取，消除輸入變量之間的相關性，提取有效信息，并降低特征空間的維數。再將提取得到的非線性主成分作為SVR的輸入，建立數學模型。測試集用來檢驗所建模型的預測能力。將測試集樣本代入模型計算，得到測試集樣本所對應的預測結果。在測試時，使用留一法來進行交叉驗證，以檢驗所建模型的預測與泛化能力[12]。本試驗使用的數據分析軟件為Matlab 2016b。

3.3　試驗及結果分析

為了檢驗所建KPCA-SVR模型的準確性及其泛化能力，采用測試樣本集對該模型的性能進行試驗驗證。KPCA-SVR模型預測結果如圖2所示。

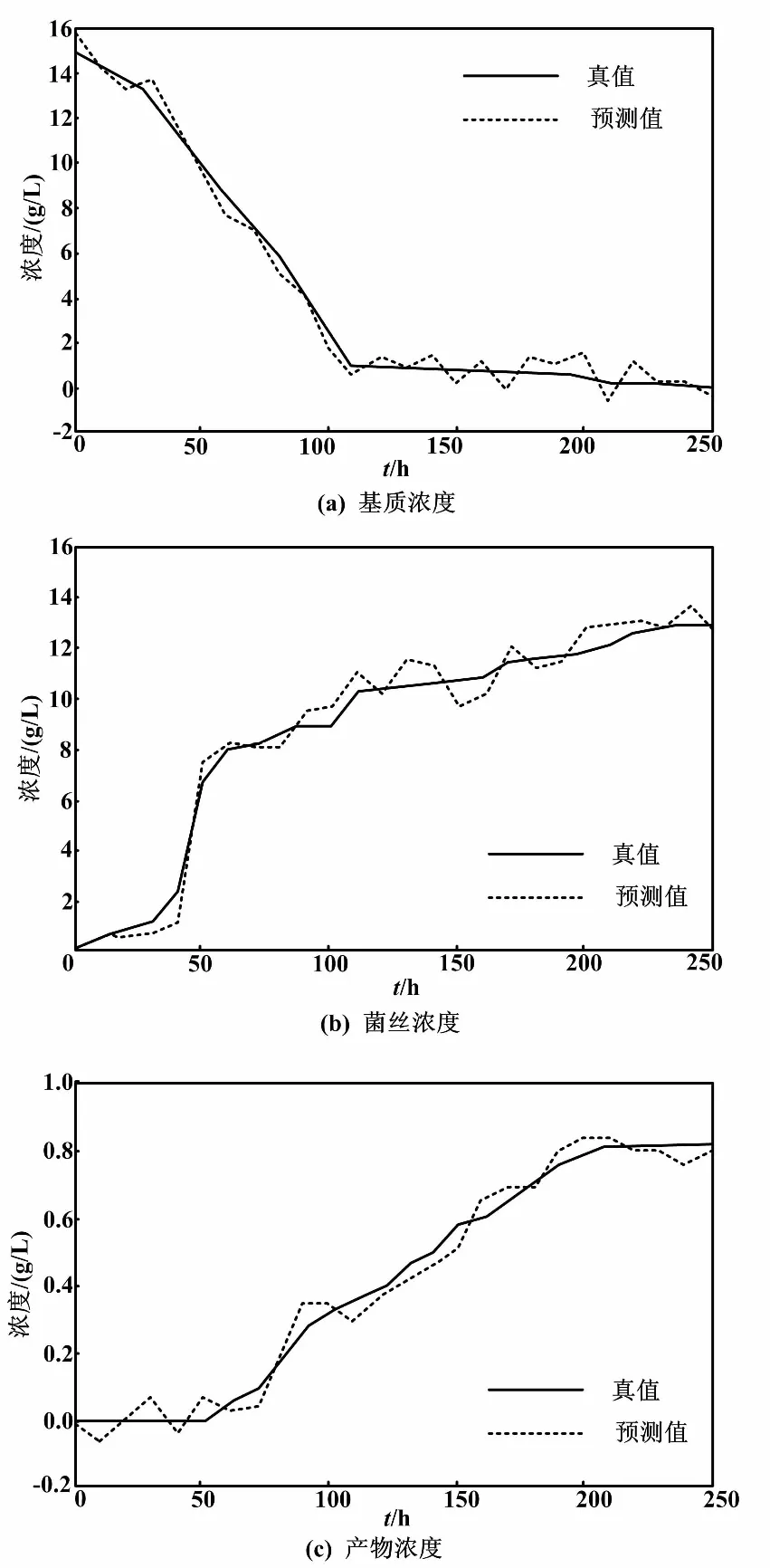
圖2　KPCA-SVR模型預測結果

從圖2中可以看出，采用KPCA-SVR軟測量建模的輸出預測值(軟測量值)，能夠很好地跟蹤發酵反應過程的真值(離線測量值)。以圖2(b)為例，模型預測值在上升過程中能夠跟蹤真值的變化，具有較好的跟蹤性能，證明了KPCA-SVR的軟測量模型能夠較準確地輸出預測值。即使只有15個批次的總樣本量，KPCA-SVR仍具有較好的泛化能力。

為檢驗KPCA-SVR方法的預測性能，將該方法與其他幾種常規的回歸預測方法進行了對比試驗。試驗中使用了偏最小二乘回歸(partial least squares regression,PLSR)、主成分回歸(principal component regression,PCR)、主成分-支持向量機回歸(principal component analysis-support vector regression,PCA-SVR)、反向傳播神經網絡(back propagation artificial neuronal network,BPANN)等幾種預回歸測方法，并采用相關系數、平均相對誤差和最大相對誤差這3個預測性能的評價指標來比較幾種回歸模型的預測效果。多種預測方法性能對比如表1所示。

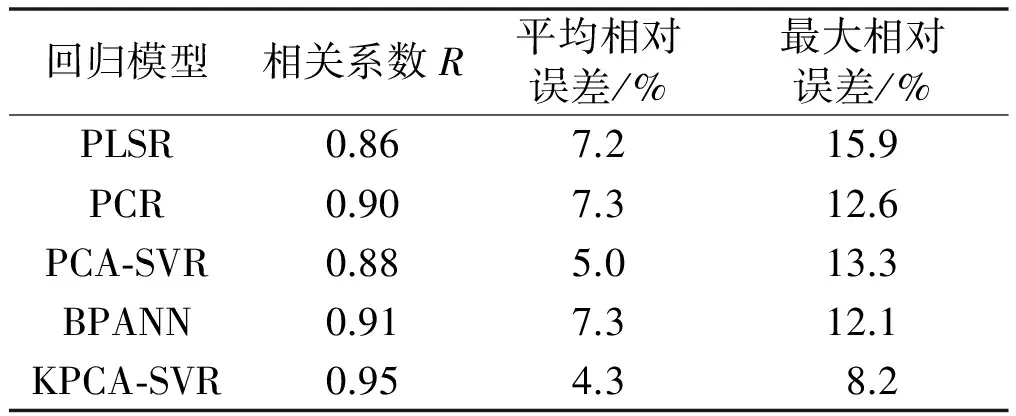
表1　多種預測方法性能對比

由表1可以看出，KPCA-SVR方法預測得到的產物濃度值的最大相對誤差為8.2%、平均相對誤差為4.3%、相關系數為0.95，為幾種回歸方法中最優的性能指標。該方法所得預測值與真值具有較好的相關性，預測值具有較高的精度，可以為青霉素發酵罐在線實時控制提供可靠的參數依據。

4　結束語

針對發酵過程中某些生化參數難以通過專用傳感器實時在線測量的問題，本文將KPCA與SVR相結合，建立了青霉素發酵過程中三個參量濃度的軟測量模型。首先，利用KPCA對樣本數據進行特征提取，剔除數據中的冗余信息，提取得到包含有效信息的主成分，達到特征降維的目的；然后，利用SVR建立青霉素發酵過程的預測模型，并與其他常規建模方法進行對比試驗。試驗結果表明，KPCA-SVR軟測量模型的測量精度高、跟蹤性能好、泛化能力強。與其他方法相比，KPCA-SVR具有更高的預測精度，在一定程度上為青霉素的優化生產提供了參數保證，是一種有效的軟測量建模方法。該軟測量方法可以滿足青霉素發酵過程產物濃度的測量要求，同時也可以用于其他類似的生化發酵過程測量。

參考文獻:

[1] 薛堯予,王建林,于濤,等.基于改進 PSO 算法的發酵過程模型參數估計[J]. 儀器儀表學報,2010,31(1):178-182.

[2] 王博,孫玉坤,嵇小輔,等.基于PSO-SVM逆的賴氨酸發酵過程軟測量[J]. 化工學報,2012,63(9):3000-3007.

[3] 黃永紅，孫麗娜，孫玉坤，等．海洋蛋白酶發酵過程生物參數的軟測量建模[J]．信息與控制，2013，42(4):506-510．

[4] 曹鵬飛，羅雄麟．化工過程軟測量建模方法研究進展[J]．化工學報，2013，64(3):788-800．

[5] 黃麗，孫玉坤，嵇小輔，等．基于CPSO與LSSVM融合的發酵過程軟測量建模[J]．儀器儀表學報，201l，32(9)：2066-2070．

[6] 吳文元，熊智華，呂寧．支持向量回歸在乙烯裂解產物收率軟測量中的應用[J]．化工學報， 2010，61(8):2046-2050．

[7] 唐志杰，唐朝暉，朱紅求．一種基于多模型融合軟測量建模方法[J]．化工學報，2011，62(8):2248-2252．

[8] 劉國海，周大為，徐海霞，等．基于SVM的微生物發酵過程軟測量建模研究[J]．儀器儀表學報，2009，30(6)：1228-1232．

[9] 孫玉坤，王博，黃永紅，等．基于聚類動態LS-SVM 的L-賴氨酸發酵過程[J]．儀器儀表學報，2010，31(2):404-409．

[10]唐勇波，桂衛華，彭濤．變壓器油中氣體的多核核主元回歸預測模型[J]．電機與控制學報，2012，16(11):92-98．

[11]張學工.模式識別[M].3版.北京：清華大學出版社，2010.

[12]嚴衍祿，陳斌，朱大洲.近紅外光譜分析的原理、技術與應用[M].北京:中國輕工業出版社，2007.

[13]THEODORIDIS S,KOUTROUMBAD K.模式識別[M].4版.北京：電子工業出版社，2010.

[14]VLADIMIR N V.統計學習理論的本質[M].張學工,譯.北京：清華大學出版社，2000.

[15]瑞明.支持向量機理論及其應用分析[M].北京：中國電力出版社,2007:152-153.