冷熱電聯供型微電網系統多目標日前優化調度

羅　平，韓露杰，孫作瀟，呂　強，陳巧勇

(1.杭州電子科技大學自動化學院，浙江 杭州 310018；2.國網浙江省電力公司杭州供電公司，浙江 杭州 310009)

0　引言

微電網系統可通過優化控制其可控發電單元和儲能系統的出力，實現系統運行成本或污染物排放量最小的優化調度目標，故近年來受到學術界和工業界的廣泛關注[1-3]。冷熱電聯供(combined cooling heating and power，CCHP)型微電網相比于普通微電網，具有運行模式多樣、能源利用率高、控制靈活、供電可靠性高以及環境污染小等特點，受到各國的廣泛重視，已經成為第二代能源技術的重點研究對象[4-6]。但由于冷熱電聯供型微電網內部的能源結構和設備之間的耦合關系復雜，特別是冷熱電聯供系統的熱電耦合現象，使得優化調度方案的確定變得非常困難。而采用 “以熱定電”或“以電定熱”的運行方式，在一定程度上起到了熱電解耦的作用，但不利于實現熱電負荷的統一協調調度[6]。

目前，針對CCHP型微電網優化調度問題，研究者們已取得了一定的研究成果[6-11]。

①文獻[6]以包含風機、光伏、熱電聯供系統、電鍋爐、燃料電池和儲能系統的并網型微電網為例，求得調度周期內各微電源的最佳出力及系統運行成本。

②文獻[7]提出了基于母線式結構的CCHP型微電網優化模型，對系統中的各設備進行了獨立建模，并采用0-1混合整數線性規劃算法對系統進行了日前經濟優化調度。

③文獻[8]將微型能源網中的能源分為冷、熱、電和氣四種形式，提出了基于集中互聯能源交換網絡的CCHP型微能源網供能構架，并采用Hessian矩陣迭代的內點法對采用該構架建立的經濟優化模型進行了求解。

④文獻[9]以經濟、環保的綜合成本為目標函數，建立了CCHP微網系統的環保經濟調度模型，并采用混沌粒子群優化算法對其進行了優化求解。該研究結果表明，蓄熱蓄冷裝置調整了燃氣輪機的出力，提高了系統運行的經濟性。

⑤文獻[10]計及光伏和熱電負荷的隨機性，綜合考慮運行費用和污染氣體排放量，建立了多目標機會規劃模型，并采用隨機模擬技術和Pareto最優解集進行了求解。

⑥文獻[11]考慮了風電的隨機性，在目前的電力市場環境下，利用場景產生和消除方法進行了微電網的熱電聯產優化調度。

但以上文獻在建立優化目標時，大多直接選定單個目標函數進行優化求解，缺少對其他相關因素的考慮；或者是通過加權或者模糊化的方法，將多目標優化問題轉換為單目標優化問題進行求解，導致調度方案適用范圍有限、調度計劃缺乏靈活性。

本文以某一居民小區日常能源供應為例，建立了以系統運行成本和環境治理成本最小為優化目標的CCHP型微電網優化調度模型。為了提高算法的求解速度和Pareto前沿分布的均勻性和多樣性，采用基于優秀粒子引導的改進粒子群算法對該模型進行優化求解，給出了夏季典型日優化調度問題的Pareto前沿。分析了某夏季典型日的多目標優化調度方案，并與“以熱定電”和“以電定熱”的運行方式的調度結果進行了對比。

1　CCHP型微電網系統模型

本文研究的CCHP型微電網系統主要由風力發電系統、光伏發電系統、燃氣輪機發電系統、空調以及儲能系統組成。風力和光伏發電系統均采用最大功率跟蹤模式發電，以最大限度地利用可再生能源[9]。微型燃氣輪機在發電的同時，將產生的煙氣余熱等低品質熱能用于驅動溴化鋰吸收式冷熱水機組制冷/熱能。儲能系統包括蓄電池和蓄熱/冷槽。空調通過調節蓄熱/冷槽、溴化鋰冷熱水機組出力與冷/熱負荷三者之間的功率平衡，達到既可作為電負荷，又可作為冷/熱源參與冷/熱負荷調度的目的。CCHP型微電網基本結構如圖1所示。

圖1　CCHP型微電網基本結構圖

1.1　燃氣輪機發電系統模型

燃氣輪機發電系統在發電的同時，將回流換熱器排出的高溫煙氣余熱用于驅動溴化鋰吸收式制冷機產生冷/熱能，能源綜合利用率可達80%以上。該系統的數學模型[12]如下：

(1)

Qgt-co=QGT×COPco

(2)

Qgt-he=QGT×COPhe

(3)

式中：Pe和ηe分別為燃氣輪機的輸出功率和發電效率；QGT為燃氣輪機高溫尾氣的煙氣余熱量；ηL為燃氣輪機的散熱損失系數；Qgt-he、Qgt-co和COPhe、COPco分別為燃氣輪機高溫尾氣余熱提供的制熱/冷量與溴冷機的制熱/冷系數。

1.2　儲能系統模型

儲能系統包括電儲能系統與熱/冷儲能系統。其中，電儲能系統選取蓄電池作為儲能設備。其儲能容量與蓄電池充放電功率應滿足[11]：

EES(t)=(1-τ)EES(t-1)+

(4)

式中：EES(t)為t時刻蓄電池的儲能容量；τ為蓄電池的自放電率；PES_ch(t)、PES_dis(t)和ηsch、ηsdis分別為蓄電池在t時刻的充/放電功率和充/放電效率。

對于熱/冷儲能系統，采用蓄熱/冷槽進行蓄熱/冷。該系統夏天可蓄冷、冬天可蓄熱。其所儲能量的計算式為[13]：

R=ρVCPεαΔT

(5)

式中：R和V分別為蓄熱/冷槽中的可用能量和可用水的體積；ρ為水的密度；CP為水的比熱容；α為蓄熱/冷槽容積的利用率；ε為蓄熱/冷槽的完善度；ΔT為蓄熱/冷槽進水溫差。

蓄熱/冷槽的動態模型[14]可表示為：

HHS(t)=(1-μ)HHS(t-1)+

(6)

式中：HHS(t)為t時刻蓄熱/冷槽的熱儲能容量；μ為蓄熱/冷槽的散熱損失率；QHS_ch、QHS_dis和ηhch、ηhdis分別為蓄熱/冷槽在t時刻的蓄熱/冷功率及蓄熱/冷效率。

1.3　空調模型

空調將電能轉換成冷能或熱能，每小時消耗的電能與產生的熱/冷能的關系可表示為：

Qec-co=PE×COPec-co

(7)

Qec-he=PE×COPec-he

(8)

式中：Qec-co、Qec-he分別為空調的制冷量與制熱量；PE為空調的輸入電功率；COPec-co、COPec-he分別為空調制冷和制熱能效比。根據不同的能效標準，空調的制冷/熱能效比的取值范圍為2.3～3.6。

2　多目標優化調度模型

選取24 h內，蓄電池、蓄熱/冷槽和微型燃氣輪機在每小時內的出力，為CCHP型微電網優化調度問題的優化變量。在滿足各單元物理約束和系統運行約束的條件下，通過合理安排可控微源和儲能系統的出力，使系統的運行成本和環境治理成本最低。

2.1　目標函數

目標函數為系統總的運行成本f1(X)和系統污染物排放治理費用即環境成本f2(X)。

f1(X)=JE(X)+JO(X)+JF(X)+JB(X)

(9)

(10)

式中：JE(X)為微電網系統與大電網的電能交互成本；JO(X)為設備的運行維護成本；JF(X)為燃氣輪機的燃料成本；JB(X)為蓄電池和蓄冷槽的折舊成本；n為污染物的種類；Vi為第i項污染物的排放治理費用；Qi(X)為第i項污染物的排放量。

因此，CCHP型微電網的目標函數可表示為：

F(X)=min{[f1(X),f2(X)]T}

(11)

2.2　約束條件

2.2.1設備物理約束

設備物理約束通常是由于設備運行的物理極限所致，需強制滿足，否則會對設備本身甚至整個微電網系統造成永久性損害。

①蓄電池。

蓄電池首先應該滿足充放電功率約束，即：

-PES_ch_max≤PES≤PES_dis_max

(12)

式中：PES_ch_max和PES_dis_max分別為最大允許的充、放電功率；PES為蓄電池功率。

通過等價轉換，式(12)的約束可轉換成兩相鄰時刻蓄電池荷電狀態(stage of charge,SOC)值應滿足的約束[15]。

SOCi+1-SOCi>δ

(13)

式中：SOCi和SOCi+1分別為兩相鄰時刻的蓄電池SOC值。在不同運行狀態下(充電或放電狀態)，δ值不同。

②燃氣輪機。

燃氣輪機發電功率Pgen(t)應當滿足功率的上、下限：

Pgen-min≤Pgen(t)≤Pgen-max

(14)

式中：Pgen-min為發電機的最小啟動功率；Pgen-max為最大發電功率，一般取額定功率值。

此外，燃氣輪機還應滿足爬坡率的約束：

(15)

式中：Pup、Pdown分別為發電機爬坡率的上、下限。

2.2.2系統運行約束

①功率和能量平衡約束。

系統在運行時，應當滿足功率平衡。

Pload(t)=Pgen(t)+PES(t)+PPV(t)+PWT(t)

(16)

式中：Pload(t)、PPV(t)、PWT(t)分別為負荷預測功率、光伏和風力預測發電功率；PES(t)為蓄電池充放電功率。

同時，系統還需滿足系統冷/熱能平衡：

(17)

式中：Qload(t)、Qair(t)分別為熱/冷負荷、空調制熱/冷量；Qhs為蓄熱/冷槽釋放的熱/冷量。

②儲能設備狀態初始時刻和結束時刻相同。

由于CCHP型微電網優化調度呈現周期性，因此，儲能設備蓄電池和蓄熱/冷槽的能量在調度周期內的初始和結束時刻應保持一致，即應滿足如下表達式。

SOCsES=SOCeES

(18)

SOCshs=SOCehs

(19)

式中：SOCsES、SOCeES和SOCshs、SOCehs分別為調度周期內初始時刻和終止時刻蓄電池的荷電狀態以及蓄熱/冷槽的儲熱/冷水平。

2.3　約束處理方法

針對如式(12)～式(15)所示的設備物理約束，采用硬約束處理的方法，即將違背約束的運行變量強制賦值為邊界值。而對于如式(16)和式(17)所表示的系統運行約束中的功率平衡約束，則采用降維處理方法[16]，即假設等式中有N個變量，選取其中(N-1)個變量作為自變量，剩余1個變量為因變量。因變量值由其他自變量的值和約束等式共同確定。由于本文研究的微電網運行在并網狀態，因此將Pgrid(t)作為因變量。

式(18)和式(19)表示的約束與儲能設備的物理約束在時間上具有耦合性，很難進行解耦處理。因此本文采用罰函數法進行處理，將違背的約束作為懲罰項加入總的運行成本，形成如式(20)所示的新的目標函數。

F′(X)=F(X)+β×|SOCi+1-SOCi|

(20)

式中：β為約束懲罰因子。

3　優化算法

為提高傳統多目標粒子群優化(multi-objective particle swarm optimization,MOPSO)算法的尋優性能，本文提出了一種基于優秀粒子指導的MOPSO算法。改進的MOPSO算法流程如圖2所示。

圖2　改進的MOPSO算法流程圖

改進的MOPSO算法先利用遺傳算法，求解以運行成本最低為目標的CCHP型微電網系統優化調度模型；再利用遺傳算法，求解以環境治理成本最低為目標的CCHP型微電網系統優化調度模型，得到相應的調度結果。將這兩個優化調度結果作為兩個個體隨機賦給多目標粒子群算法的初始種群，并利用MOPSO算法對原始的多目標優化問題進行求解，得到對應的Pareto前沿。

4　算例分析

4.1　基礎數據

CCHP型微電網的優化調度周期為1 d，單位調度時間Δt為1 h。微型燃氣輪機額定輸出功率為60 kW，最小啟動功率為18 kW，發電效率為0.3，散熱損失系數為0.16；使用燃料為天然氣，其熱值為9.7 Wh/m3，價格為3.3元/m3。假設微型燃氣輪機的余熱煙氣全部供給溴化鋰吸收式冷熱水機組，則該機組的制冷性能系數為1.2，制熱性能系數為0.9。空調的制冷和制熱性能系數為2.7。蓄電池和蓄熱槽的充放率為0.9，折舊成本為0.05元/(kWh)，容量為200 AH，兩相鄰時刻SOC最大變化值為0.3。

微電網系統和大電網的污染物排放系數以及處理成本如表1所示。

表1　污染物排放系數以及處理成本

夏季典型日參數預測值如圖3所示。

圖3　夏季典型日參數預測值曲線

4.2　夏季典型日優化的調度結果分析

改進算法夏季典型日調度方案的Pareto前沿如圖4所示。

圖4　改進算法的Pareto前沿

對圖4中Pareto前沿最左邊的一個點，即運行成本最低時系統的調度結果進行分析。此時，運行成本和環境成本分別為1 051.1元和755.0元。當運行成本最低時，電功率調度結果如圖5所示。

圖5　電功率調度結果(運行成本最低)

從圖5中可以看出：對電能單元調度結果起主要調節作用的是蓄電池和微型燃氣輪機。蓄電池在4:00、5:00、17:00、18:00、19:00、24:00處于充電狀態，在12:00、14:00、15:00、21:00、22:00處于放電狀態，其余時刻不工作。微型燃氣輪機在11:00、12:00、13:00、14:00、15:00、16:00、20:00、21:00處于啟動狀態且以額定功率運行，其余時刻處于停機狀態。也就是說，蓄電池在整個調度周期內主要經歷了兩次充放電。其中：4:00～5:00、5:00～6:00這兩個時段大電網電價較低，蓄電池處于充電狀態；而在12:00～15:00這一時段，蓄電池大部分處于放電狀態,并在電價相對較高的時段以最大功率放電。

空調作為可變負荷，將電能轉換成冷能，與蓄冷槽和溴化鋰吸收式制冷機共同調節系統內冷負荷的供需平衡。當運行成本最低時，熱/冷功率調度結果如圖6所示。

圖6　熱/冷功率調度結果(運行成本最低)

由圖6可知，溴化鋰吸收式制冷機工作狀態與微型燃氣輪機的運行狀態一致，即在11:00、12:00、13:00、14:00、15:00、16:00、20:00、21:00處于工作狀態。蓄冷槽在5:00、18:00、19:00處于儲能狀態，在12:00、14:00、21:00、22:00處于放電狀態。在電價較高時，由于微型燃氣輪機的啟動，系統內的冷負荷大部分由溴化鋰吸收式制冷機來承擔，在此基礎上的部分冷負荷缺額則由空調和蓄冷槽共同承擔；在電價相對較低時，冷負荷幾乎全部由空調制冷量來承擔，例如1:00、2:00、3:00、4:00、6:00、7:00、8:00、9:00、17:00、23:00。

由以上分析可知，蓄冷槽的運行狀態與蓄電池相似，但總的充放量相對較少。這是因為空調的制冷性能系數較高，本文選取2.7。這意味著空調消耗1 kWh的電量可“搬運”2.7 kWh的冷量，使得蓄熱槽在轉移冷能時的成本相對低廉，即蓄冷槽的能量轉移和存儲收益(即通過高價蓄能低價放出賺取的差價)沒有蓄電池那么明顯。另一方面，蓄冷槽的折舊成本也較低。如果想要賺取利潤，蓄冷槽放出能量的收益要大于儲能和折舊成本的總和。因此，在差價相對較小的情況下，蓄冷槽賺取利潤的空間也相應減少。

4.3　“以熱定電”方式運行的調度結果分析

當系統采用“以熱定電”的方式運行時，可通過求出滿足冷負荷需求時微型燃氣輪機排放的煙氣余熱量，得到對應的發電功率。此時，微型燃氣輪機應首先滿足冷負荷需求。若最大運行功率仍不能滿足其冷負荷的需求，則需空調制冷；若微型燃氣輪機的發電量在滿足電負荷以后仍有剩余，則可向大電網出售。運行周期結束后，其運行成本和環境成本分別為1 936.1元和359.9元。“以熱定電”方式下，電功率調度結果如圖7所示。

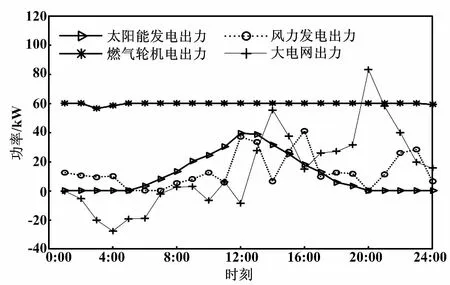
圖7　電功率調度結果(以熱定電)

由圖7可知，燃氣輪機在整個周期內基本以額定功率運行，這主要是由于冷負荷過大引起的。由于冷、電負荷大小不匹配，當電負荷較小而冷負荷較大時，微型燃氣輪機發出的多余電量一方面可用于空調補充缺額冷負荷所用電量，另一方面可售予大電網。當電負荷和冷負荷都較大時，缺額的電負荷功率只能向大電網購買。

4.4　“以電定熱”方式運行的調度結果分析

當系統采用“以電定熱”的方式運行時，根據日前預測的電能負荷以及風、光功率出力，可求出凈電負荷。通過凈電負荷確定微型燃氣輪機的出力，若此時的凈電負荷大于微型燃氣輪機的額定功率，則缺額功率由大電網補充。微型燃氣輪機在發出電量的同時，若產生的供冷量仍不能滿足冷負荷，則缺額冷負荷由空調制冷彌補；若此時溴化鋰吸收式制冷機組產生的冷量有剩余，則丟棄。運行周期結束后，系統的運行成本和環境成本分別為1 719元和 362.9元。“以電定熱”方式下，電功率調度結果如圖8所示。

圖8　電功率調度結果(以電定熱)

由圖8可知：在1:00～13:00這一時段，凈電負荷小于微型燃氣輪機額定功率，因此完全由微型燃氣輪機供應。此時由溴化鋰吸收式制冷機組制取的冷量不能滿足冷負荷的需求，缺額的冷負荷只能由空調補充，因此大電網在此時段一直處于售電狀態。在14:00～21:00這一時段，冷負荷和電負荷都較大，微型燃氣輪機即使以額定功率運行，仍不能滿足系統的缺額電功率，只能通過向大電網購電的方式進行彌補。而在24：00時，電功率調度結果出現了丟棄制冷量的現象。這也暴露了系統“以電定熱”狀態運行的弊端，即冷、電負荷不匹配，而電負荷相對冷負荷較高時，會產生能量浪費的情況。

5　結束語

本文針對某大型住宅小區并網模式運行下CCHP型微電網系統的日前優化調度問題，以系統運行成本和污染物治理成本最低為目標，將微型燃氣輪機、蓄電池、蓄熱/冷槽三類可控單元中每時段的出力作為優化變量，在滿足系統運行以及模型約束的條件下，建立了日前多目標優化調度模型。

為了提高算法的求解速度、完善Pareto前沿的性能，采用基于優秀粒子指導的MOPSO算法對模型進行求解，并與“以熱定電”和“以電定熱”這兩種運行方式的調度結果進行了對比。對比結果表明，在后兩種運行方式下，微型燃氣輪機的出力或者完全跟蹤冷/熱負荷，無法參與電能調度；或者完全跟蹤電負荷，無法參與冷熱負荷調度。而CCHP型微電網系統由于存在儲能系統，可以通過合理的調度方式實現熱電的協調、統一調度，提高了能量的利用率，實現了系統的優化運行。

參考文獻:

[1] 劉增環，李潔.基于Multi-agent的微電網運行與研究控制[J].自動化儀表,2015,36(4):13-17.

[2] AKI H.The penetration of micro CHP in residential dwellings in Japan[C]//Power Engineering Society General Meeting.IEEE,2007:1-4.

[3] 董昕昕，孫偉卿，張巍，等.能源互聯網背景下的多能源輸送網絡聯合建模[J].自動化儀表，2017，38(1)：16-19.

[4] 張巍,董昕昕,孫偉卿,等.能源互聯網中的綜合能源系統研究[J].自動化儀表,2017,38(1):12-15.

[5] 袁越,曹陽,傅質馨,等.微電網的節能減排效益評估及其運行優化[J].電網技術,2012,36(8):12-18.

[6] 李正茂,張峰,梁軍,等.含電熱聯合系統的微電網運行優化[J].中國電機工程學報,2015,35(14):3569-3576.

[7] 王成山,洪博文,郭力,等.冷熱電聯供微網優化調度通用建模方法[J].中國電機工程學報,2013,33(31):26-33.

[8] 徐青山,曾艾東,王凱,等.基于Hessian內點法的微型能源網日前冷熱電聯供經濟優化調度[J].電網技術,2016,40(6):1657-1665.

[9] 戚建文,任建文,渠衛東,等.冷熱電聯供微網環保經濟調度研究[J].電測與儀表,2016,53(16):90-95.

[10]顧偉,吳志,王銳.考慮污染氣體排放的熱電聯供型微電網多目標運行優化[J].電力系統自動化,2012,36(14):177-185．

[11]徐立中,楊光亞,許昭,等.考慮風電隨機性的微電網熱電聯合調度[J].電力系統自動化,2011,35(9):53-60.

[12]魏兵,王志偉,李莉,等.微型燃氣輪機冷熱電聯產系統經濟性分析[J].熱力發電,2007,36(9):1-5.

[13]崔恒志,黃奇峰,楊世海,等.冷熱電聯供型微電網容量規劃優化研究[J].江蘇電機工程,2013,32(3):39-41.

[14]吳雄,王秀麗,別朝紅,等.含熱電聯供系統的微網經濟運行[J].電力自動化設備,2013,33(8):1-6.

[15]LUO P,SUN Z X,ZHU S C,et al.The dynamic multi-objective optimal dispatch of grid-connected micro grid[C]// Proceedings of the 35th Chinese Control Conference,2016:2804-2809.

[16]洪博文,郭力,王成山,等.微電網多目標動態優化調度模型與方法[J].電力自動化設備,2013,33(3):100-107.