基于時變T-Copula模型的中國股市國際一體化研究

談勇賢，郭 頌

（上海財經大學 金融學院，上海 200120）

0 引言

股市一體化作為經濟全球化和金融自由化下資本市場的主要發展趨勢，其學術研究價值不言而喻。迄今為止，諸多學者分別基于不同的樣本和不同的檢驗方法對全球范圍內的股市一體化現象進行了探討研究。早期的研究主要關注發達國家股市之間的一體化進程，從研究方法來看，早期多數學者考察股市的一體化進程基本都是采用傳統的VAR脈沖響應、多元GARCH簇方法以及線性Granger因果檢驗等分析方法。然而上述研究方法仍然存在一些不足：其一是只能考慮時間序列有限階滯后影響，通常金融時間序列之間具有復雜的因果關系，伴隨著序列非平穩、自相關、異方差以及共線性等影響，而上述檢驗模型很難實現甄別，以致最后的結論可靠性較差。其二是上述檢驗方法從本質上來說都是一種線性因果關系檢驗，經濟全球化和金融自由化使得國際金融市場面臨結構更復雜的互動關系，金融危機的教訓提示應當更加關注股票市場極端價格波動引發的傳染效應，顯然傳統的溢出效應層面的考察并不能有效滿足復雜結構下的股票市場一體化進程的研究。其三是上述檢驗模型通常只能靜態地刻畫股市聯動以及股市傳染。

與現有文獻相比，本文具有如下特點：一是在一體化研究框架下，分別從聯動性與傳染性兩個方面全面系統地分析了全球范圍內的股市一體化程度，形成對現有文獻的有益補充。二是分析了以金磚國家為代表的中國市場的股市世界一體化程度，同時基于中國市場系統內部，研究了中國股市與其他金磚國家股市的聯動性、傳染性，并且從股市傳染強度視角，比較了金磚五國股票市場的系統重要性；基于成熟市場系統，對比研究了中國股市的世界一體化程度與成熟市場的世界一體化程度；三是首次基于時變動態Copula技術刻畫了股票市場相關結構，并在此基礎上，通過Kendall秩相關系數與尾部相關系數分別刻畫不同股市之間的聯動性與傳染性；四是在股市一體化模型構建與實證研究中，充分考慮到不同股市之間的非線性相關結構以及一體化程度的動態變化特征，全面展現不同股市之間相關結構的演化過程。

1 模型構建、樣本選取和數據說明

1.1 Copula函數估計相關結構

通常情況下，股票市場價格收益率序列往往存在“波動性集聚”，呈現“尖峰厚尾”的非對稱特征，并且多數情況下伴隨著“杠桿效應”，傳統的分布統計分析不能很好地擬合收益率序列的分布，也不能預測股票價格在極端情形下的變化特征。另外，傳統的GARCH模型往往將擾動項設定為正態分布，然而當時間序列存在厚尾狀態時，其異常波動情形比在正態分布下更容易發生，這時將擾動項設定為偏t分布可以更精確地刻畫價格波動過程。綜合考慮，本文對各個股票價格收益率建立ARMA(p,q)-GJRGARCH(1,1,1)-偏t模型以刻畫各國指數的邊緣分布。模型表達形式如下：

第一個方程為股票收益率的條件均值方程，p和q為其滯后階數，其最優值通過BIC準則確定；第二個方程表示對股票收益率殘差序列εi,t進行標準化處理；第三個方程為股票收益率的條件波動方程，其中wi為常數參數，αi為滯后平方殘差項系數，表示未來信息對股票價格的影響程度，βi波動滯后方差項系數，表示波動的記憶性，即上期波動對于當期波動的影響程度。第四個方程為標準化殘差序列ei,t服從峰度參數為ηi，偏度參數為λi的偏t分布。

接下來，對各個國家指數邊緣分布進行結構Copula函數擬合。根據Copula函數在單調增變化下Copula函數保持不變的性質可知，由于ri,t和rj,t分別是ei,t和ej,t的單調增函數，因此對收益率序列ri,t和rj,t之間相關結構的研究可以轉換為對其標準化殘差序列ei,t和ej,t之間相關結構的研究。在擬合Copula函數之前，需要對標準化殘差序列ei,t和ej,t進行概率積分變換，以得到滿足二元Copula函數變量定義域的U（0，1）時間序列，如果經過積分概率變換后的時間序列ui,t和uj,t均服從均勻分布，則可以進行Copula函數擬合估計。考慮到標準化殘差序列ei,t和ej,t均服從偏t分布，本文選擇橢圓類的T-Copula函數進行結構相關性估計。T-Copula函數本質上是一個結構相關參數為ρ和自由度參數為φ的二元t分布函數，同時，由于Copula函數中的結構相關參數ρ為二元函數分布下的相關性度量，所以可以充分反映各種線性以及非線性相關性信息。

然而上述T-Copula函數的相關結構參數ρ是靜態的，不能夠反映標準化殘差序列ei,t和ej,t（也就是指數收益率序列ri,t和rj,t）的動態變化關系，需要將相關結構參數進行結構性動態演化，基于Manthos Vogiatzoglou（2010）等學者的研究，最能夠有效描述T-Copula函數條件相關矩陣的動態過程是DCC過程，所以本文假設相關結構參數ρ的條件相關矩陣服從動態DCC(1,1)過程，從而得到動態時變相關結構參數ρt，具體表達式如下：

其中，是et的樣本協方差矩陣，是主對角元素為Qt平方根，非對角線元素為0的2×2階矩陣，模型參數約束滿足φ+ψ＜1;φ,ψ∈(0,1)。

1.2 聯動性與傳染性的刻畫

接下來，本文對股票價格收益率進行聯動性效應與傳染性效應刻畫。聯動性的最主要特征是股票價格同步波動的相關性，即ri,t和rj,t同步上漲或者下跌，能夠有效描述這一特征的相關性度量被稱為一致性度量。經常使用的一致性度量是Kendall秩相關系數τ，其具體定義如下：

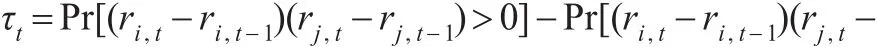
如果表示成Copula函數的形式，則為：

而根據傳染性的定義，本文關心的是當某個股票價格異常上漲或下跌（主要是下跌）波動時對于另一個市場股票價格的影響程度，即二者之間的尾部相關性。能夠有效描述這一特征的相關性度量被稱為尾相關度量。最經常使用的尾相關度量是上下尾相關系數λu和λl，其具體定義如下：

而當Copula函數為時變T-DCC-copula函數時，尾相關度量上下尾相關系數和與時變結構相關系數ρt之間具有如下的關系：

1.3 樣本選取與數據說明

成熟市場方面，本文選取老牌資本主義發達國家，主要是德國、法國、英國以及日本。對于世界市場，作為全球最具影響力的股市，美國股市的變化往往左右著其他國家股市的變化，其國際影響甚為重要，毫無疑問是最重要的世界市場。代表性指數選取方面，依次選取中國上證綜合指數作為中國股市指數代表；成熟市場方面，選取英國富時100指數、德國法蘭克福DAX30指數、法國CAC40指數、日經225指數作為成熟市場指數代表；選取美國S&P500指數作為世界市場指數代表。這些指數也是多數學者的普遍選擇，上述各個國家市場指數分別記為：CN（中國）、BR（巴西）、SA（南非）、IN（印度）、RE（俄羅斯）、USA（美國）、GM（德國）、FR（法國）、UK（英國）和JP（日本）。

本文選取的樣本期間是從2005年1月4日至2015年11月20日。刪除因節假日不同等導致交易日指數缺失的數據，最后得到2093組日數據。指數日收益率通過對日收盤價做一階對數差分得到，為了減少計算誤差，日收益率均乘以100，即rt=100*ln(Pt/Pt-1)，其中rt為指數在t日的日收益率，Pt為指數在t日的收盤價，Pt-1為指數在t-1日的收盤價，這樣就得到了指數的日收益率序列。

2 實證分析

各個國家市場指數日收益率序列的基本描述性統計如下頁表1所示。

由表1可知，在樣本考察期內，中國市場整體收益率均值水平均高于成熟市場以及世界市場，而作為世界市場的美國市場收益率平均水平保持在0左右。與之相對應的是中國市場的收益率標準差也要高于成熟市場以及美國市場，這說明中國市場在保持高收益率的同時，其自身風險狀態也比較高。所有指數的偏度值均小于0，說明上述指數收益率均呈現后尾狀態，而峰度值都超過了4，說明尖峰效應明顯。所有指數的JB檢驗統計量都很顯著，說明上述指數序列都不服從標準正態分布，基于傳統正態分布的溢出效應檢驗會導致偏差。Q（10）檢驗表明，在滯后10階、10%的顯著水平下，除了德國市場指數以外，其他市場指數均具有自相關性，而ARCH效應檢驗表明，在滯后10階，1%的顯著性水平下，上述指數序列仍然具有明顯的條件異方差性，呈現顯著的“波動性集聚”狀態；ADF單位根檢驗和KPSS平穩性檢驗均表明，在1%的顯著水平下，上述各個指數都是平穩的。因此，總體來看，所有指數序列都具有尖峰、后尾和條件異方差的特點。

表1 各國指數收益率的統計性描述

考慮到上述特點，接下來本文將使用ARMA(p,q)-GJRGARCH(1,1,1)-偏t模型來模擬上述指數序列的邊緣分布，其結果如表2所示。

表2 ARMA(p,q)-GJRGARCH(1,1,1)-偏t模型的參數估計結果

由表2可知，在條件均值方程ARMA(p,q)中①本文設定ARMA(p,q)中的最高滯后階數為5階，并且依據BIC準則來確定最優滯后階數，結果發現所有的股票指數序列的最優滯后階數為：p=0，q=0，即條件均值模型實際上為ARMA(0,0)形式，故參數只有一個μ。，所有股市均值溢出效應均不顯著。在條件波動方程GIRGARCH(1,1,1)參數估計結果中，在10%的顯著性水平下，常數項w均很顯著；對于滯后平方殘差項的系數α而言，中國市場指數的系數α在10%的顯著性水平下都很顯著，而世界市場以及除了德國之外的其他成熟市場的系數α均不顯著，這說明中國股票市場當期價格容易受到前期新信息的顯著影響，而前期相關信息卻不會對成熟股票市場以及世界股票市場當期價格產生顯著性影響，成熟股票市場的有效性程度高于中國市場；對于波動滯后方差項的系數β來說，所有市場指數的系數值在1%的顯著性水平下都很顯著，這說明，無論是中國市場還是成熟市場以及世界市場，股票價格波動都具有記憶性，即前期價格波動會顯著影響后期股票價格波動；在偏t分布方程的參數估計結果中，所有股市指數的非對稱參數λ和峰度參數η在1%的顯著性水平下都很顯著，說明所有股市指數序列都具有尖峰和后尾特征，并且呈現有偏狀態。Q(10)、ARCH分別是針對標準化殘差序列et進行的滯后10階自相關檢驗與異方差檢驗，檢驗結果表明在5%的顯著性水平下，標準化后的殘差序列均已無明顯自相關與異方差特征。而對標準化殘差序列et經過積分變換后的序列ut行K-S分布擬合檢驗，結果表明在1%的顯著性水平下所有序列ut都通過了K-S檢驗，說明它們均服從U(0,1)分布。綜合來看，建立ARMA(p,q)-GJR GARCH(1,1,1)-偏t模型可以很好地對上述股票指數邊緣分布進行描述，并且可以發現不同股市價格波動的一些重要信息，從而可以建立時變Copula模型來準確研究不同國家股市之間的相關結構。

3 中國股市與成熟股市的世界一體化差異

下頁表3給出了成熟股市市場指數與美國S&P 500指數的T-DCC-Copula函數擬合結果。

由表3可以看出，在10%的顯著性水平下，所有二元分布T-Copula函數自由度參數均很顯著，說明T-Copula函數可以較好地度量股票指數的相關結構，同時每個相關結構DCC動態演化參數（尤其是第二個參數）顯著性很高，說明與中國市場股市相比，成熟股市與世界股市的相關性動態變化特征更加明顯，所以時變T-DCC-Copula模型可以有效地刻畫成熟股市與世界股市整體相關結構及其動態變化特征。

下頁圖1給出了包括德國、法國、日本以及英國在內的老牌發達資本主義國家成熟市場與美國市場的動態Kendall系數變化情況，同時為了進行比較研究同時還給出了中國股市與美國股市的動態Kendall系數變化情況。

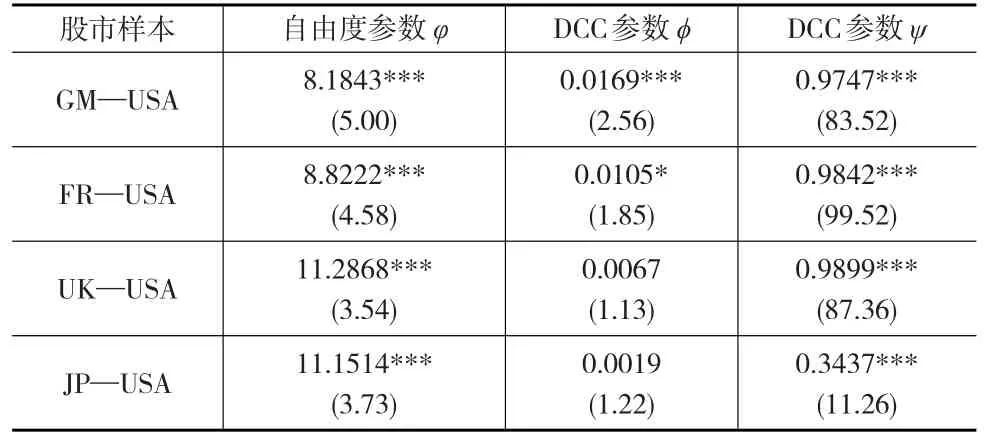
表3 時變Copula模型的參數估計結果

圖1 中國股市、成熟股市與世界股市的動態Kendall系數

由圖1可以看出，發達國家的成熟市場的世界一體化程度也不盡相同，其中德國、法國以及英國股市與美國股市的動態Kendall系數走勢波動情況基本一致，系數平均水平為0.4左右，而波動區間也基本是在[0.3，0.5]上，而日本股市與美國股市的動態Kendall系數走勢情況卻與上述國家不同，其系數值的平均水平為0.1左右，并且其波動區間也是位于[0.095，0.015]上，整體來看，成熟市場的股市世界一體化程度要普遍高于中國市場的世界一體化程度，依據經濟基礎假說，這主要與其對外貿易活躍程度有關。

就金融危機以及歐債危機期間的聯動性來看，歐洲成熟市場的動態Kendall系數表現基本一致，即在2008年之后，歐洲成熟市場與美國市場的動態Kendall系數逐漸升高，并且在金融危機與歐債危機期間保持較高的聯動程度，動態Kendall系數值基本維持在0.5左右，并且波動較小，并且高聯動程度的持續時間較長，基本上直到2014年才逐漸下降到正常水平，而后又開始逐漸升高，這說明，在危機期間，成熟市場與世界股市的聯系較穩定時期更為密切，并且危機事件對于成熟股市的世界一體化聯動性影響時間較長。相比之下，在危機期間，日本市場的動態Kendall系數表現和中國股市有些相同，并沒有出現明顯的系數變化情況，而是維持之前的平均水平上下波動，說明危機事件對于亞洲股市的世界一體化聯動程度影響很低，不過總體來看，日本股市的世界一體化程度仍然高于中國股市。

圖2顯示了在樣本考察期內，發達國家成熟股市與美國股市之間的動態上下尾部系數（或者）走勢及其波動情況，即股市傳染性的動態變化情況。德國股市與美國股市的動態上下尾部系數（或者）最高，波動區間為[0.1，0.3]，平均水平超過了0.2，接下來是法國股市與英國股市，動態上下尾部系數（或者）平均水平大致為0.15，大致也在[0.1，0.3]上波動，而日本股市與美國股市的動態上下尾部系數（或者）卻較低，其平均水平大約為0.016，波動區間為[0.0155，0.017]，但是仍然高于中國股市以及大部分新興股市與美國股市的動態上下尾部系數（或者），并且就整體水平來看，與中國市場相比，成熟市場的世界一體化程度較高，同時相互之間的傳染性也較高。

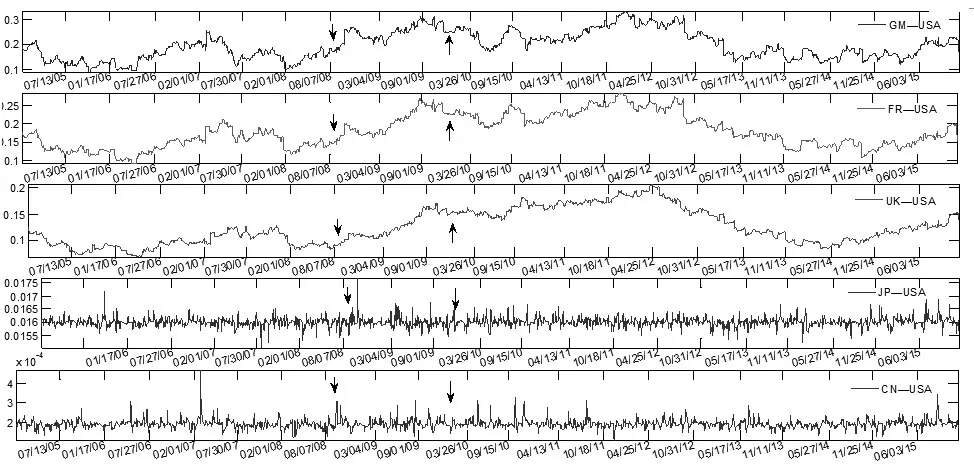
圖2 中國股市、成熟股市與美國股市的動態尾部系數

在圖2中同樣標注了美國金融危機以及歐洲次貸危機發生的時間節點，通過該時間節點前后的動態上下尾部系數（或者λl）走勢波動情況，可以窺探危機事件對于成熟股市與世界股市在危機期間的傳染性情況。具體來說，2008年金融危機發生后，歐洲成熟股市與世界股市的傳染性急劇上升，遠遠超過正常水平，之后隨著歐洲債務危機的發生，由于歐洲成熟市場與債務國之間的政治經濟聯系程度較高，歐債危機的持續蔓延再次推動傳染性逐漸升高，達到樣本時間內的最高處，并且一直持續到2012年底左右，才開始逐漸下降，而日本股市與美國股市之間的傳染性在金融危機發生后迅速升高，但是又迅速下降，危機事件的沖擊效應持續時間很短，而中國股市和美國股市之間的傳染性在危機期間波動不大，基本上不明顯，所以上述事實說明了隨著股市一體化程度的不同，某個國家市場受到金融危機的影響持續時間也不同，當與世界股市的聯動性較高時，金融危機的傳染持續時間較長，而當聯動性程度較低時，受危機影響的程度較低。

因此，成熟股市與世界股市之間的傳染性整體水平較高，尤其是在金融危機以及歐債危機期間，傳染性不再是某個時間節點的特有現象，而是持續顯著的長期性現象。當危機信息蔓延時，成熟市場股市收益率的波動由于在短期內劇烈波動，以此對投資者的心理預期產生影響，使得成熟市場與世界市場的股票價格異常波動，并且由于預期性因素的持續性，這種異常波動產生的傳染性也持續顯著，所以在股市世界一體化進程中要格外關注傳染性。

4 結論及建議

本文基于聯動性與傳染性的視角，考慮到股市結構的時變與非線性特征，運用動態Copula技術刻畫股票市場相關結構，進而通過秩相關系數與尾相關系數度量不同股市間的聯動性與傳染性，分析了中國股市與世界股市的聯動性、傳染性，并且對比研究了中國股市的一體化程度與成熟市場的一體化程度。結果表明：就中國市場的世界一體化程度而言，隨著中國市場與世界股市聯動性的提高，股市間的傳染性也在提高，尤其是在金融危機以及歐債危機期間；當前階段中國股市的世界一體化程度要比中國市場一體化程度要低。無論是聯動性還是傳染性，成熟市場的世界一體化程度普遍比中國市場尤其是中國股市要高，成熟股市與世界股市的聯動性在金融危機期間得到顯著提高，同時傳染性也得到顯著提高，并且持續時間較長，所以隨著股市世界一體化程度的提高，股市間的傳染并不再是某一時間或時點的特有現象，而是一種持續顯著的較長期性現象。

繼續推進中國股市國際一體化進程是應對經濟全球化以及提升國際影響力的必然途徑，而當前中國股市的整體國際一體化程度較低，所以一方面要繼續加強同世界市場在金融開放、資本流動等方面的深化合作，逐漸提高我國股市的系統重要性與國際影響力；另一方面要時時關注一體化進程中的風險傳染，在股市國際化較低的情況下，股市傳染是短期股市價格異常波動的特有現象，所以當下我國股市國際化進程要以穩為主，循序漸進，避免激進式改革可能引發的外界風險渠道傳染，而隨著股市國際化程度的提高，股市傳染將會是較長期的持續性現象，因此長遠來看，提高資金配置效率，完善價格發現機制，提高市場有效性才能避免市場主體估計不足或者過度反應，從容應對外界風險沖擊。

參考文獻：

[1]Dooley M，Hutchison M，Transmission of the U.S.Subprime Crisis to Emerging Markets：Evidence on the Decoupling Recoupling Hypothesis[J].Journal of International Money and Finance，2009,28(8).

[2]Modi A G，Patel B K，Patel N R.The Study on Co-movement of Selected Stock Markets[J].International Research Journal of Finance and Economics，2010，(47).

[3]Aloui R，Alissa M S B，Nguyen D K，Global Financial Crisis，Extreme Interdependences，and Contagion Effects：The Role of Economic Structure?[J].Journal of Banking and Finance,2011，35(1).

[4]Samarakoon P.Stock Market Interdependence，Contagion，and the U.S.Financial Crisis：The Case of Emerging，Frontier Markets[J].Journal of International Financial Markets，Institutions and Money，2011,(21).

[5]馬君璐，吳蕾，靳曉婷.美國危機向亞洲中國市場傳染過程中的多米諾效應研究[J].世界經濟，2012，(6).

[6]何光輝，楊咸月，陳詩一.人世以來中國證券市場動態國際一體化研究[J].經濟研究，2012，(10).

[7]趙進文，蘇明政，邢天才.未預期收益率，傳染性與金融危機——來自上海市場與世界市場的證據[J].經濟研究，2013，(4).

[8]王健.中美股市聯動性——基于極大重疊離散小波變換的研究[J].世界經濟文匯,2014,(2).

[9]梁琪,李政,郝項超.中國股票市場國際化研究：基于信息溢出的視角[J].經濟研究,2015，(4).

[10]劉源,邱麗萍,劉濤.ARCH簇模型在股市風險價值測度中的應用[J].特區經濟,2017,(1).