一種處理內置離群值投資風險準備金的方法
艾小娟
(西北工業大學 人文與經法學院,西安 710072)
0 引言
有序金融市場中,市場穩定運行,資本價格變化是一個連續、光滑的運行曲線,投資者投資收益或風險為資產標的、投資者風險態度、投資期限等變量的函數。但是,當出現如國家政策重大調整、行業突發公共危機、自然災害不可抗力等重大不確定性事件時,金融市場價格尤其是相應行業的金融指數會出現短期內的跳躍式變化,給金融市場投資者帶來不確定的投資風險。從統計角度看,市場波動下的跳躍式數據就是金融市場價格運行曲線上的尖峰點或波谷點,在極端情況下甚至表現為單個或多個的離群值(outlier)。統計學上,離群值又叫逸出值,它是指在一系列數據中凸顯于其他數據的一個或幾個數值較大或較小者,有的甚至呈多倍差異的遞增或縮減。根據chanwennt準則,如果某數值偏離被測對象統計均值的概率低于1/2N(N為被測樣本個數),則判定該數值為離群值,應該予以慎重考慮或調整處理。本文擬推介一種處理離群數據的統計方法,即改進鏈梯法,并以投資期內出現了異常事件的金融投資為研究案例,運用改進鏈梯法,對其風險損失在進展年的增量準備金及累計準備金作出估計。
1 鏈梯法的一般算法
流量三角形興起于精算領域,是一種用于預測事故在保險進展年可能發生理賠的次數或金額的精算方法。流量三角形結構(見表1),其間,為一隨機變量組,Xi,j表示事故在第i年發生后第j進展年的增量賠付額。令第n+1年為精算年,則當i+j≤n時,Xi,j是已知的,其數據集合為上流量三角形,當i+j>n(以后各年)時,Xi,j未知,其數據組合成下流量三角形,即為要預測的未決賠付額。

表1 流量三角形數據結構圖
在具體預測時,經典算法有分離法、賠付金進展法、鏈梯法等,本文擬運用鏈梯法實施風險損失預測。令Xi,j為事故年i、進展年j的增量賠付,Si,j為累計賠付,則有:

其中,進展因子序列{ }fj→j+1|j=0,1,...,J-1 及其無偏估計滿足:
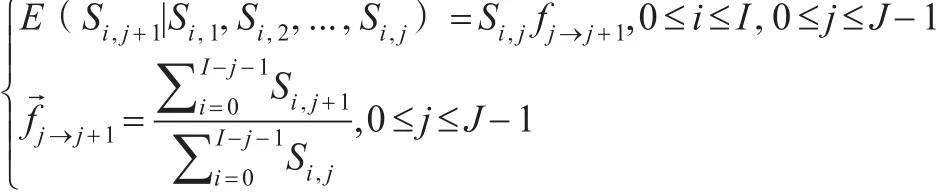
于是,得到鏈梯法一般算法:
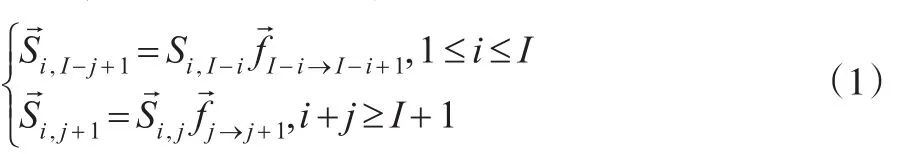
由式(1)可得事故年i時點的賠付估計量-Si,I-i,(1≤i≤I),進展年總賠付估計量
2 改進的鏈梯法及其對離群數據的診斷與調整
本文根據鏈梯法思想,改進進展因子模型,測試出現離群數據時的賠付損失問題,并進一步識別離群數據可能出現的位置,診斷導致離群賠付的原因。為此,首先定義進展因子流量三角形:
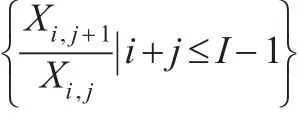
單一離群數據可干擾1~2個進展因子,于是,本文用增量中位數表述累計均值,得到第j個進展年的進展因子如下:
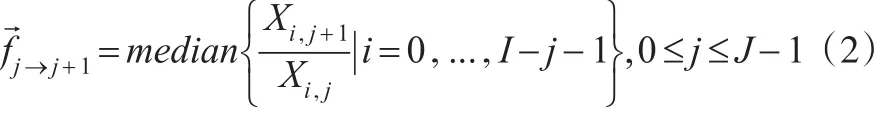
2.1 對 j=0進展年離群數據的識別與調整
令增量賠付損失額Xi,j( )i+j≤I服從泊松分布,且相互獨立,又令其中,為殘差,φ為分散參數,滿足:

可得流量三角形上三角數據個數N=(I+1)(I+2)/2,其中,p=2I+1為待估參數個數。接下來計算上三角增量賠付殘差,保持上三角(即i+j≤I期間)的累計賠付不變,于是其累計賠付真實值可用測算擬合值替代,從事故發生年i到第j年的累計賠付擬合值→通過第j+1進展年的賠付除以相應的進展因子得到,公式如下:
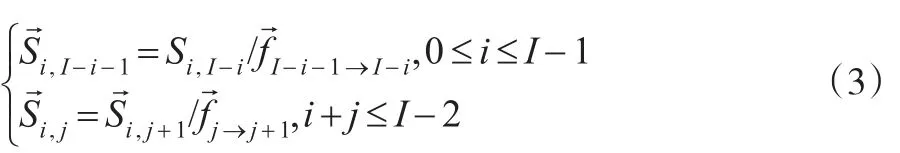

聯立公式(2)至公式(4),得到上三角增量賠付擬合值,如公式(5)所示:
接下來考察上三角(即i+j≤I期間)有(I+1)(I+2)/2個殘差的情景,此時的進展年(j(j=0))賠付額存在離群數據,這些賠付離群數據是我們要調整的對象。令進展年j(j=0)及進展年j(j=1)的賠付殘差分別為rk,0、rk,1。rk,1為離群數據和非離群數據時的調整賠付Xk,0為:

2.2 對 j≠0進展年離群數據的識別與調整
首先計算進展年j(j≠0)的進展因子,參照進展年0的算法,可得的計算公式,如下:


在判定賠付殘差ri,j統計量特征后,運用箱線圖(Boxplot)判定規則考察賠付殘差的離群特性。如果賠付殘差具有離群特性,則離群殘差k)由以下公式得出:

于是,調整殘差可通過逆向變換得到,再參照公式(3)至公式(6)得到調整離群數據后的增量賠付及累計賠付
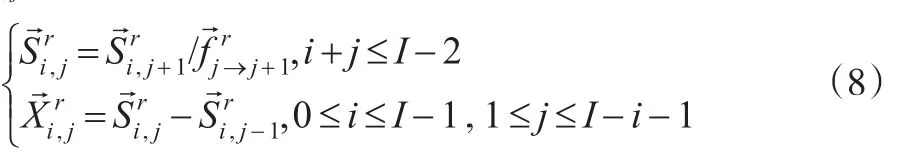
其中進展因子為:
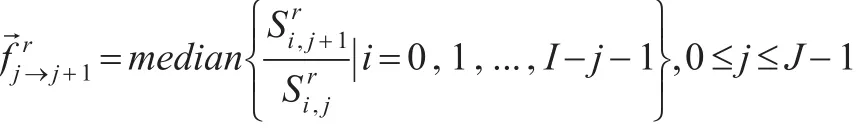
3 實證分析
本文研究案例選自高盛2006年(投資基年,i=0)投資的經典案例,2008年由美國金融市場次貸危機,最后演變成全球性的世界金融危機,所以,本文的事故發生年即為2008年(i=2),根據其公司投資的報表數據,本文將其繪制成如下流量三角形(見下頁表2所示)。
根據表2流量三角形數據實施鏈梯法估計,得到預測結果如下頁表3所示,可以看出,鏈梯法得出的投資風險損失準備金為
表4(見下頁)是采用改進了的鏈梯法對未來投資風險損失準備金的估計結果。從計算結果可以看出,由于表2的原始數據中存在8個離群數據,它們分別為事故年i=2的所有增量損失X2,0、X2,1、X2,2、X2,3、X2,4、X2,5、X2,6、X2,7。相比于其他數據,X2,0至X2,7相對較高,這可能是由2008年美國資本市場爆發的次貸危機造成的。為了消除這單一不確定性因素,接下來擬采取改進了的鏈梯法對這些異常離群值實施調整,并據此預測未來增量損失額及累計損失準備金。從表4可知,采用改進了的鏈梯法估計的投資風險準備金為僅為,與表3結果存有顯著不同。
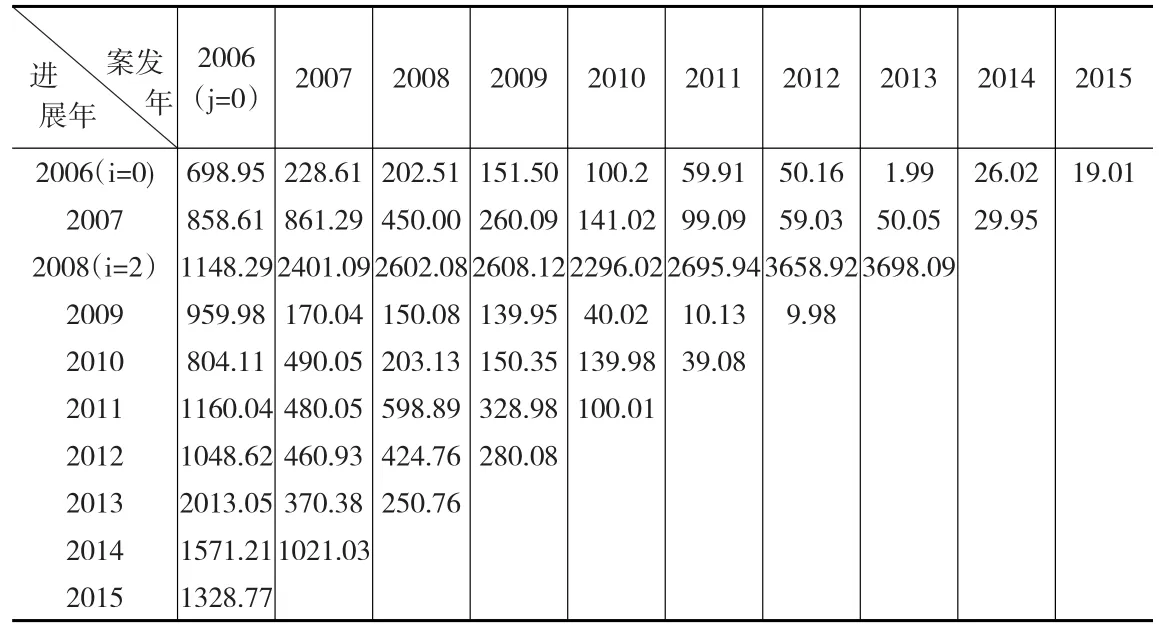
表2 高盛公司經典投資案例真實流量三角形 (單位:萬美元)

表3 鏈梯法對未來風險損失準備金的估計 (單位:萬美元)
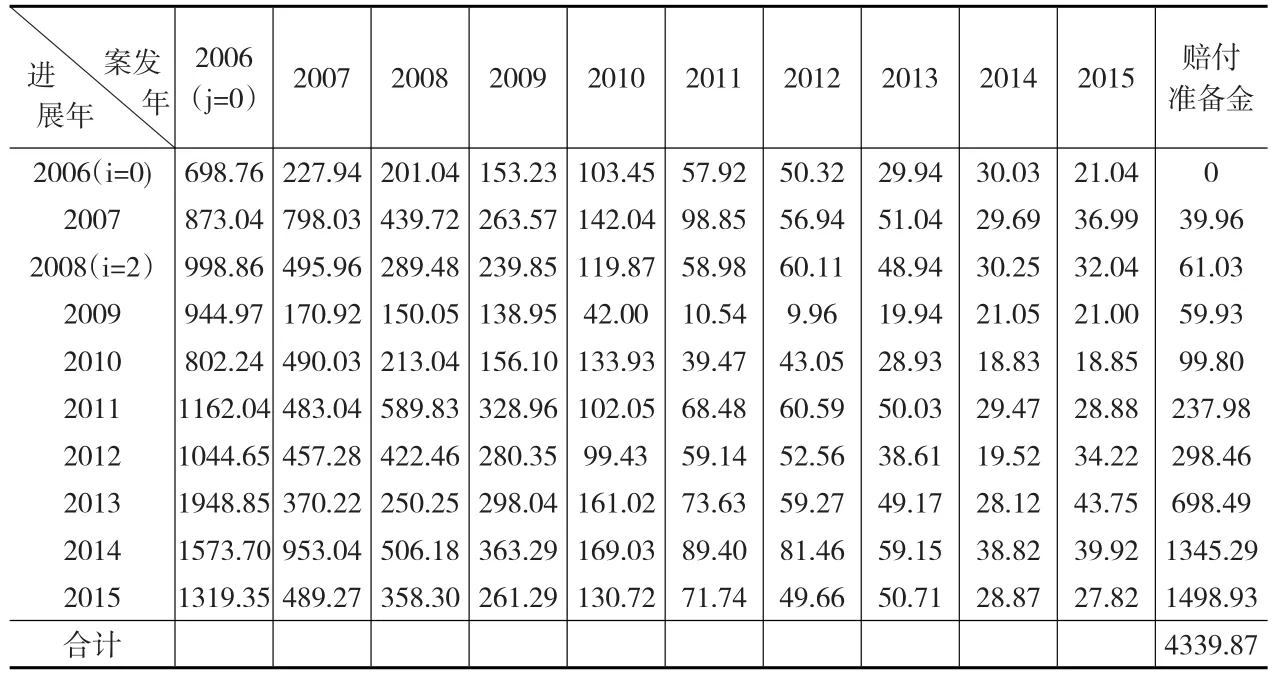
表4 改進鏈梯法對未來風險損失準備金的估計 (單位:萬美元)
從以上分析可知,相對于傳統鏈梯法,改進了的鏈梯法對事故發生后的未來損失準備金的估計明顯趨于平緩。因為這種算法剔除了現實中存在的過于極端的不確定性,所以此方法預測出的賠付準備金更接近于理性情況,更能穩定市場各參與主體。當然,盡管極端事件發生的概率很小,在作出決策時,我們也要考慮現實經濟生活中可能出現的重大不確定性事件(如2008年由于次貸危機事件確實引發了全球經濟危機),分析異常離群數據出現的位置,實施更為穩健的風險金融政策,比如可以結合改進鏈梯法對未來損失準備金的估計與傳統鏈梯法估計的差額,設定投資風險損失基金,確保金融投資企業有一個安全的資金邊際。
4 結束語
實證研究表明,采用改進了的鏈梯法對投資風險準備金實施預測是可行的。改進鏈梯法能夠診斷離群值并確定其所處位置,并據此調整風險損失流量三角形,進而調整風險損失準備金。可見,通過改進了的鏈梯法能夠平滑風險賠付,減少離群數據對風險損失賠付估計的影響,穩定金融市場各參與主體,避免市場非理性行為的發生。當然,在投資實務中,也要高度重視離群值對投資決策的影響,因為無視離群數據,可能造成低估風險損失,在防范不當之時,極端情況可能導致投資主體破產。所以,本文也要分析離群數據出現的原因,判斷其對未來收益的可能影響,并對改進鏈梯法的預測值加以修正或設置風險損失準備基金,以提高投資主體金融決策的穩健性與準確性,確保投資的金融邊際安全。
參考文獻:
[1]Stefanski L A,Carroll R J,Ruppert D.Optimally Bounded Score Functions for Generalized Linear Models With Applications to Logistic Regression[J].Biometrika,1986,73(2).
[2]Rousseeuw P,Leroy A.Robust Regression and Outlier Detection[J].New York:Wiley 1987.
[3]Tay F E H,Cao L.Application of Support Vector Machines Financial Time Series Forecasting[J].Omega:The International Journal of Management Science,2001,(29).
[4]Hess K T,Schmidt K D.A Comparison of Models for the Chain-Ladder Method.HESS K T,SCHMIDT K D.Insurance:Mathematics andEconomics.2002,31(3).
[5]Lauer F,Bloch G.Incorporating Prior Knowledge in Support Vector Machines for Classification:A Review[J].Negro Computing,2008,71(7).
[6]陳明鏡.準備金“鏈梯法”與三種過原點回歸模型[J].西南民族大學學報:自然科學版,2011,(4).

