帶有缺失數據的分位數回歸模型的參數估計

丁先文，陳建東，朱小芹

（江蘇理工學院 數理學院，江蘇 常州 213001）

0 引言

關于線性回歸模型的統計分析一直都是統計學的熱點研究課題。基于最小二乘估計方法對回歸模型進行統計分析已被廣泛研究并應用在各個領域。然而，普通的最小二乘回歸（均值回歸）只能描述協變量對響應變量均值的影響，而不能刻畫對響應變量條件分布的影響，而且當誤差的方差比較大或數據中存在異常點時，最小二乘方法的有效性將備受挑戰。Koenker和Bassett（1978）[1]提出了分位數回歸模型，隨后對該模型進行了系統的研究和推廣。通過估計不同的條件分位數函數，分位數回歸可以系統地刻畫協變量對響應分布的影響。此外，分位數回歸模型對誤差分布不作任何假設，這使得分位數回歸模型得到了許多研究者的深入研究并在各領域得到了廣泛應用。關于分位數回歸模型的研究進展和詳細介紹，見Koenker（2005）[2]。

在許多實際問題中，如抽樣調查、臨床試驗、經濟調查等，由于被調查對象不愿回答問題等各種因素，經常會導致缺失數據的產生。對缺失數據的統計研究是近年來統計學的熱點研究問題。Little和Robin（2014）[3]定義了三種不同的數據缺失機制，即完全隨機缺失、隨機缺失（MAR）和不可忽略缺失。在實際運用中，通常假設數據的缺失機制是MAR，即缺失數據只與完全觀測的數據有關。在對缺失數據進行統計分析時，一種常用的方法是只用觀測數據進行統計推斷，這在缺失率較大時會產生較大的統計偏差；另一種方法就是對每一個缺失值采用某種統計方法進行插補，然后對插補后的數據集進行統計分析。有關缺失數據方面的介紹，見Little和Robin（2014）[3]。

近年來，對帶有缺失數據的分位數回歸模型的統計分析引起了一些研究者的興趣。如Sherwood（2013）[4]考慮了協變量隨機缺失下分位數回歸模型的參數估計問題；Liu和Yuan（2016）[5]基于經驗似然方法研究了加權分位數回歸的參數估計問題。然而，他們的方法都考慮了協變量隨機缺失并只利用了觀測數據信息進行分析，這在數據的缺失率較大時會帶來較大的估計誤差。關于響應變量隨機缺失下分位數回歸模型的統計分析很少有文獻報道。李乃醫等（2015）[6]研究了響應變量隨機缺失下非線性回歸模型的參數的經驗似然置信域問題。本文研究了響應變量隨機缺失下分位數回歸模型的參數估計問題，利用參數插補方法對缺失的響應變量進行多重插補，然后基于插補后的數據集對回歸模型進行參數估計。計算結果表明該方法在缺失率較大的情況下也可以得到有效的參數估計。另外，提出的方法對數據中的異常值并不敏感且當誤差分布為重尾分布時，也有較好的估計結果。

1 模型

1.1 參數估計方法

考慮下面的線性回歸模型：

其中Yi與Xi分別表示響應變量及p維協變量，β是p維的回歸系數，εi為具有未知分布函數的隨機誤差項。在給定Xi的條件下，令Yi的τ條件分位數為βτ且滿足其中 0＜τ＜1 。設 {Xi,Yi,為來自模型（1）的獨立同分布的隨機樣本，其中Xi可被完全觀測，Yi可能缺失。假定δi=1表示Yi可觀測，δi=0表示Yi缺失。本文假定Yi的缺失機制為隨機缺失（MAR）,即 πi=P(δi=1|Xi,Yi)=P(δi=1|Xi)，πi在文獻中常被稱為傾向得分（Propensity score）。

對響應變量隨機缺失的情形，參數估計可采用成對刪除方法，即：

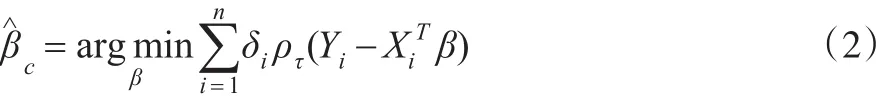
其中ρτ(t)=t(τ-I(t≤0))為檢查函數，I(.)為示性函數。這種估計方法在缺失率較大的情形下，估計量的偏差會變大，使得估計結果不可信。處理缺失數據的另外一種常見的方法是考慮對每個缺失的響應變量行多次插補，然后基于插補后的數據集進行參數估計。令{y:F(y|Xi)≥u}是Yi在給定協變量Xi下的第u個條件分位數，其中u為來自均勻分布的一個隨機數，F(y|Xi)是給Y在給定協變量Xi下的條件分布函數。注意到，在響應變量Yi隨機缺失下，有F(y|X=Xi,δi=1)=F(y|X=Xi,δi=0)成立，這樣就有Qu(yi|X=Xi,δi=1)=Qu(yi|X=Xi,δi=0)。在這里，本文假設線性模型Qu(Yi|Xi)=XTiβu。在MAR的假設下，E{δiXi[I(Y＜XTiβu)-u]}=0。

因此，可以得到βu的一個相合估計為：

相比于只利用觀測數據進行參數估計，該估計方法即使在缺失率較大時也可以得到一個穩健的參數估計結果。另外，與通常的非參數插補方法相比，即使協變量維數p很大時，該方法也是可行的。

1.2 計算方法

關于分位數回歸模型的參數估計，通常的計算軟件都可實現。目前較為流行和廣泛采用的方法是利用R軟件中的軟件包quantreg進行計算。假設為來自模型（1）的獨立同分布的隨機樣本，不失一般性，假定前n1個Yi可觀測，后n-n1個Yi不可觀測，即將原始樣本分為兩部分。模型的參數估計過程如下：

（1）隨機產生m個均勻分布的隨機數{u1,u2,...,um}；

（3）基于觀測數據{Xk,k=n1+1,...,n}和步驟（2）的結果，對缺失的Yi進行插補，即對每個Yk，其插補值為

以上計算過程中的（2）和（4）可以調用R中的quantreg軟件包實現。

2 模擬計算

為實施模擬，本文從以下模型中產生數據：

其中β=(1,2,3)T為三維待估參數向量，對應的Xi的每一個分量都獨立同分布于標準正態分布，Yi根據模型產生，模型誤差服從以下分布：M1：標準正態分布N(0,1)；M2：自由度為3的t分布t(3)；M3：混合正態分布0.1N(0,1)+0.9N(0,10)；M4：混合拉普拉斯分布 0.1Lap(0,1)+0.9Lap(0,10)。假設缺失概率其中,γ的取值為以下兩種情形：C1：γ=(0.85,1.50,1.50,0.85)T；C2：γ=(-1.80,0.50,1.50,0.85)T，相應的響應變量Yi的缺失率分別為25%和60%。本文對缺失的Yi進行多重插補，插補的次數設定為m=10次。通過多次模擬可知，插補10次后，參數估計結果就很穩定，并且插補后的估計結果對插補次數并不敏感。將模擬計算獨立重復1000次，計算結果如表1和下頁表2所示。表中Bias表示1000次重復模擬的參數估計的均值與真實值的絕對偏差，SD表示1000次模擬的參數估計的標準差，RMS表示1000次模擬的參數估計的均值與真實值之差的平方和的平方根。

表1 缺失率為25%時的模擬計算結果

表2 缺失率為60%時的模擬計算結果

從表1和表2可以看出：

（1）對兩種估計方法，減少缺失率有利于減小估計的偏差和提高估計的精度；

（2）針對不同的誤差M1至M4，基于文中提出的插補方法得到的參數估計結果比基于完全觀測數據得到的結果具有較小的Bias、SD和RMS，這說明提出的多重插補方法可以減小估計偏差并能提高估計的有效性；

（3）基于插補方法得到的參數估計結果在不同的分位點處表現都很好。

3 總結

本文研究了在響應變量隨機缺失下分位數回歸模型的參數估計問題。傳統的基于成對刪除數據的估計方法沒有利用所有可觀測到的協變量的信息，在數據的缺失率較大時容易產生較大的偏差，降低了估計效率。本文首先基于觀測數據得到了模型的參數估計；其次在MAR假定下，對缺失的響應變量進行了多重插補，從而得到了插補后的數據集；最后基于插補后的數據集對分位數回歸模型進行參數估計。該插補方法在數據的缺失率較大時依然有效，并且由于采用的是參數插補方法，即使當協變量維數很高時，方法依然有效。模擬計算說明了該方法的有效性。本文的方法可以應用于微觀經濟、醫藥追蹤試驗和抽樣調查等帶有缺失數據的各種領域。

參考文獻：

[1]Koenker R,Bassett Jr G.Regression Quantiles[J].Econometrica：Journal of the Econometric Society,1978.

[2]Koenker R.Quantile Regression[M].Cambridge：Cambridge University Press,2005.

[3]Little R J A,Rubin D B.Statistical Analysis with Missing Data[M].New Jersey：John Wiley&Sons,2014.

[4]Sherwood B,Wang L,Zhou X H.Weighted Quantile Regression for Analyzing Health Care Cost Data With Missing Covariates[J].Statistics in Medicine,2013,32(28).

[5]Liu T,Yuan X.Weighted Quantile Regression With Missing Covariates Using Empirical likelihood[J].Statistics,2016,50(1).

[6]李乃醫,李永明,韋盛學.缺失數據下非線性分位數回歸模型的光滑經驗似然推斷[J].統計與決策,2015，(1).