不確定需求下基于魯棒優化的層級設施選址模型

萬 波，陳 琴

（江漢大學a.商學院；b.文理學院，武漢 430056）

0 引言

隨著社會的進步與生活水平的提高，顧客需求的多樣化程度越來越高，需要建立不同層級的設施，以滿足顧客的多樣化需求。層級設施在服務領域廣泛存在，典型的層級設施包括醫院、學校以及急救中心等。層級設施選址在規劃過程中需要考慮諸多的不確定因素，例如顧客對服務的需求具有不確定性，特別是當前城鎮化過程中人口波動所導致的需求波動。此外，選址決策的長期性導致旅行時間、建設成本等相關因素也會隨著時間發生變化。因此，研究不確定性需求下的層級設施選址問題具有重要的意義。

處理不確定性問題的方法包括隨機規劃、模糊規劃以及魯棒優化方法等。隨機規劃需要事前給出不確定參數的概率分布，這在多數情況下是較困難的，而模糊規劃要求事先給出不確定參數的模糊隸屬度函數，其具有一定的主觀性。魯棒優化起源于魯棒控制理論，可以很好地解決由于數據不準確而導致的決策風險，從而得到數據不確定情況下的魯棒最優解[1]。魯棒優化包括相對魯棒優化、絕對魯棒優化以及偏差魯棒優化等，相對后悔值模型通過控制各種情景下目標值與最優值的波動來保持最優解的穩定性，是一種典型的相對魯棒優化模型[2]。

Vincenzo等[3]針對需求、成本等市場因素不確定的情況，以各種情景下相對后悔值的期望值最小化為目標，建立了帶容量限制的魯棒優化模型。胡丹丹和楊超[4]針對截流選址問題中流量的不確定性，建立了魯棒隨機截流選址模型。韋憶立和高詠玲[2]利用相對遺憾值約束來控制實際成本與最優成本的差距，建立了配送中心選址的魯棒優化模型。何珊珊等[5]引入控制參數對各需求點應急物資的需求進行控制，建立了多目標魯棒優化模型。高雷阜等[6]針對不確定因素對應急物資儲備庫選址決策的影響，建立了相應的魯棒優化模型。以上文獻僅對單一層級設施選址問題進行研究，而利用魯棒優化模型對多層級設施選址問題研究鮮見于文獻。Pehlivan等[7]建立了設施與顧客均具有嵌套性的層級設施選址模型，對法國上塞納省婦產科醫院選址進行規劃；Teixeira和Antunes[8]提出了帶容量限制的層級設施選址模型，對學校選址問題進行了研究；Ratick等[9]建立了最大覆蓋層級選址模型，對醫療設施選址問題進行了研究；陳志芬等[10]建立了應急設施層級選址模型，并利用實驗進行了模擬。以上文獻對層級設施選址研究沒有考慮需求的不確定性。本文考慮層級設施選址過程中的需求不確定性因素，建立了基于魯棒優化的層級設施選址模型，并以武漢市某區的醫院為例進行實例分析。

1 問題背景與模型符號

1.1 問題背景

本文的研究對象為多層級的醫院類設施選址問題。首先，醫院服務系統的顧客需求具有不確定性。由于受城鎮化因素的影響，大批農民涌入城市，導致就醫需求出現波動；另外，城市內部的流動性較大，也導致就醫需求不確定性增加。其次，醫院所提供的服務具有層級性與嵌套性。服務設施的層級性是由需求多樣性和需求偏好所決定的，即需要建立多級醫院，以滿足不同層次的需求，這也是國家分級診療制度的要求；同時，層級設施根據其服務水平可分為嵌套型與非嵌套型，本文研究的醫院是典型的嵌套型設施，即高級別設施除提供該層級特有的服務外，還應覆蓋低級別設施所提供的服務。此外，醫院選址需要考慮成本與效用的均衡性。一方面，要考慮成本因素，各級醫院設置最小與最大容量約束；另一方面，醫院需要盡可能發揮資源的利用效率，為全體人民提供醫療服務。

1.2 模型符號

模型有關參數定義如下：

H：表示需求點的需求層次、設施點的服務層級的集合；I：需求點集合，i∈I；

J：設施候選點集合，j∈J；

k：需求點的需求層次和設施點的服務層次，k∈H；t：設施點的服務等級，t∈H；

dij：需求點i到設施候選點j的距離；

uiks：情景s下需求點i第k層的需求量；

bjt：點j所設立t級醫院承擔的最高級服務的最低需求量（下文稱為服務能力最小值）；

Bjtk：點j所設立t級醫院提供的第k層服務的最大服務能力（下文稱為服務能力最大值）；

wjks：情景s下點j承擔的第k層需求量。

同時定義如下的決策變量：

xijks：情景s下如果需求點i第k層需求由點j服務，則xijks=1，否則為0；

yjt：如果點j被選中為t級醫院，則yjt=1；否則為0。

2 模型建立

2.1 p-魯棒優化模型

p-魯棒優化模型是一種相對后悔值模型。設p為相對后悔值限定系數，p≥0；S為情景集，對于特定的情景s而言，Ps為確定的最小化問題，設Ps的最優目標值為，X為所有情景S下問題Ps的可行解，zs(X)為情景s對應的目標值，當時，稱X為問題Ps的p-魯棒解稱為相對后悔值[11]。

p-魯棒優化模型為：

式中，qs為情景s發生的概率；Ω為可行解空間[12]。

2.2 基于魯棒優化的層級設施選址模型

本文建立了基于魯棒優化的層級設施選址（Hierarchical Robust，HR）模型。該模型以實現各情景下的期望需求加權距離最小化為目標，同時考慮各級需求全覆蓋、服務水平的嵌套性、不同層級設施的服務能力約束以及需求就近分配等因素[13]。

其中，（1）式為目標函數，表示各種情景下期望需求加權距離最小化；（2）式對情景s下的需求加權距離進行定義；（3）式表示任意情景下各需求點的所有層級的需求均能得到滿足；（4）式表示各設施候選點只允許建立唯一等級的設施；（5）式表示服務的嵌套性，即設施為相同層級或者低層級的需求提供服務；（6）式表示各情景下設施承擔的各層次的需求量等于由該點服務的所有需求點的對應層次的需求量之和；（7）式表示最小容量約束；（8）式表示最大容量約束；（9）式為魯棒約束；（10）式表示就近分配；（11）式表示決策變量的取值范圍。

3 求解算法

對給定的情景s，若不考慮約束條件（9），則模型HR為確定性分層（Hierarchical Deterministic，HD）優化模型；對給定的情景集S，模型HR為基于情景的分層隨機（Hierarchical Scenario，HS）優化模型：

模型HD和模型HS為混合整數線性規劃模型，模型HR是在模型HS的基礎上加上線性約束（9），因此，模型HR也為混合整數線性規劃模型。而混合整數線性規劃問題是一個典型的NP困難問題，一般沒有多項式時間算法，難以在有效時間內求得最優解。

遺傳算法是一種智能的、有效的優化算法，它根據目標適應度函數對每個個體進行評價，按照優勝劣汰的進化規則不斷得到新的種群，搜索優化種群中的最優個體，從而求得滿意解[14]。由于遺傳算法具有自組織、自適應、自學習性以及并行性等特點，且該算法簡單易行，本文利用遺傳算法求解HR模型，具體算法如下。

步驟1：編碼，產生初始種群P0。

染色體使用整數編碼，表示不同需求點處待建醫院的層級。其中，0表示相應的需求點不建立醫院，1、2、3分別表示相應的需求點建立一、二、三級醫院，如表1所示。隨機產生N條染色體，構成一個初始種群P0。

表1 染色體結構

步驟2：按就近原則進行需求點分配。

（1）將需求點分配給最近的待建設施點；

（2）計算每個設施點分配到的需求量，判斷是否滿足最大服務能力約束，如果是，則將該需求點分配給該設施點，結束；如果否，則轉（3）進行需求點的重新分配；

（3）將未予以分配的需求點分配給次近的待建的設施點，轉（2）重新進行檢查；若繼續不滿足，則分配給第三近的待建的設施點，依此類推；若全部設施點均不能滿足，則將該需求點分配給就近的待建的設施點，結束。

步驟3：利用親和度函數進行約束條件控制。

為保證所建立的醫院能夠正常盈利并提供較好的服務質量，采用罰函數法將約束（7）至約束（9）整合到目標函數中，以δ1,δ2,δ3依次表示約束（7）至約束（9）的懲罰因子，親和度函數定義為：

若As1＞0,則在情景s下未能滿足最小服務能力約束（7）；若As2＞0,表示在情景s下未能滿足最大服務能力約束（8）；若As3＞0,表示在情景s下未能滿足魯棒約束（9）。分析可知，滿足全部約束條件的解，其目標函數Z值一定等于其親和度函數值A。

步驟4：求初始種群P0的目標值。

步驟5：交叉和變異，產生子種群Q0，求其目標值和親和度。

步驟6：采用精英策略產生新的種群R0。

步驟7：判斷是否滿足結束條件，如果否，轉步驟2；否則結束[15]。

4 實例分析

本文以武漢市某區為例，模型相關參數取值如下：設H={k|1,2,3}分別代表三個級別的需求層次與服務層級；t∈H={1,2,3}表示三個層級的醫院級別。設該區有50個需求點，即假設所有需求點均為設施候選點，即J=I[16]。不同層級的醫院對不同層次需求的服務能力不同，Bjtk為j點所設立t級醫院對k級需求的最大服務能力，設0,0;500,1000,0;800,1000,2500}。bjt表示在j點設立t級醫院的最低服務需求量，設bjt={bj1,bj2,bj3}={300,700,1700}。uiks為情景s下需求點i第k層需求的需求量，uik1由統計規律得出，為了模擬城鎮化過程中需求增長的情況，令uiks=uik(s-1)(1+5%),i∈I,k∈H,s∈S，即按每一需求點對各層次需求增長5%來設置情景。設定種群內染色體數為200，交叉概率為0.7，變異概率為0.0876，懲罰系數{{1000,1000,10}，最大迭代次數count=3000。

4.1 算法分析

4.1.1 遺傳算法的收斂性分析

取p=0.2來討論算法的收斂性。由下頁圖1可知，遺傳算法對于求解該問題具有較好的收斂性，當迭代次數count=1913時目標函數收斂，其值收斂于12776。

4.1.2 遺傳算法的有效性分析

HR模型是一個典型的線性優化問題，因此可用LINGO求取最優解。將遺傳算法與LINGO所得結果進行比較，結果如下頁表2所示。表中結果顯示，當p≥0.1時，遺傳算法所求得的滿意解和LINGO求解得到的精確解的相對偏差Δ＜2%，說明相比LINGO而言，遺傳算法具有較高的求解質量。然而，在各種p值情況下，遺傳算法的時間效率遠高于LINGO。因此，遺傳算法求解HR模型具有較高的效率，能夠在較短的時間內獲得滿意解。

圖1 遺傳算法的迭代次數與目標函數值關系圖

表2 遺傳算法與LINGO結果比較

4.2 模型的魯棒性分析

最大相對后悔值是當p值確定時，各種情景下相對后悔值的最大值，最大相對后悔值是度量HR模型的魯棒性的重要指標，最大相對后悔值越小，模型的魯棒性越強[2]。令HD、HR的需求加權距離分別為，當p確定時，令模型HR的相對后悔值，則可求出各種情景下的，令，則可求出p值確定情況下的最大相對后悔值。利用遺傳算法所求出的各種p值的最大相對后悔值，見表3所示。

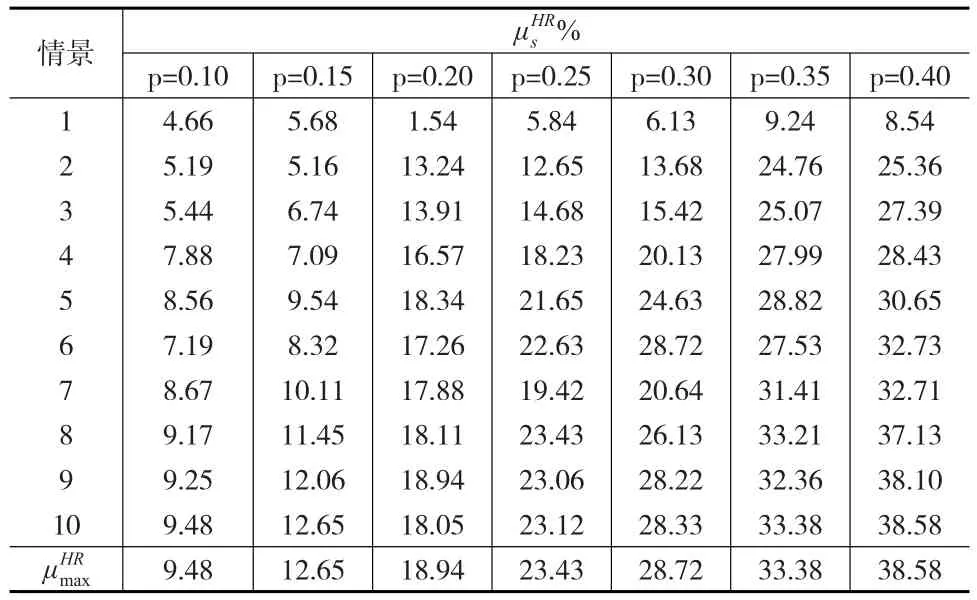
表3 不同p值的最大相對后悔值一覽表

圖2 目標函數值和最大相對后悔值隨p值變化的情況

為直觀起見，用圖2表示目標函數值和最大相對后悔值隨p值變化的情況。由圖2可知，隨著p值的增加，目標函數值呈下降趨勢，即期望旅行成本呈下降趨勢，而最大相對后悔值呈上升趨勢，兩者呈背反規律。這說明p值較小時模型的魯棒性較好，但要為此付出較高的成本代價，決策者需要根據實際情況進行權衡，選擇合適的p值，既減少不確定因素對決策的影響，降低決策風險，同時保證總成本在可控制的范圍之內。

4.3 不同情景概率對HR求解結果的影響

表4為當p=0.1時，不同情景概率下HR模型求得的目標函數值和醫院選址方案。本文選取了4種情況，每一種情況與后一種情況相比而言，q1至q5逐步增大，而q6至q10逐步減少。由表4可知，4種情況下的目標函數值逐漸遞增，這是因為各情景下的不同需求點對各層級的需求量逐步遞增，前幾種情景對應的需求加權距離更小所致。對比4種情況，醫院選址方案有較大變化，說明情景概率對選址結果產生重要影響。

表4 不同情景概率下模型HR的求解結果

5 結束語

針對城鎮化背景下服務設施的層級性與需求的不確定性特點，本文構建了基于魯棒優化的層級選址模型，利用遺傳算法進行求解，并以武漢市某區的醫院選址問題為例進行了案例分析。結果表明，遺傳算法具有較好的收斂性和較高的求解效率。p值較小時模型的魯棒性較好，但要為此付出較高的成本代價，決策者需要根據實際情況進行權衡，選擇合適的p值，使模型的魯棒性能和總成本都在可接受的范圍內。同時，當p值確定時，不同的情景概率對設施選址方案具有重要影響。

參考文獻：

[1]戴軍,關賢軍.大規模應急救援資源配送點選址魯棒優化研究文獻綜述[J].物流技術,2014,33(1).

[2]韋憶立,高詠玲.含時間約束的配送中心選址和能力規劃的魯棒優化[J].統計與決策,2015,(1).

[3]Vincenzo D R,Hartmann E,Gebhard M,Wollenweber J.Robust Capacitated Facility Location Model for Acquisitions Under Uncertainty[J].Computers&Industrial Engineering,2014,(71).

[4]胡丹丹,楊超.a-魯棒隨機截流選址問題的模型和算法[J].中國管理科學,2008,16(6).

[5]何珊冊,朱文海,任晴晴.不確定需求下應急物流系統多目標魯棒優化模型[J].遼寧工程技術大學學報,2013,32(7).

[6]高雷阜,于冬梅,趙世杰.不確定需求下應急物資儲備庫選址魯棒優化模型[J].中國安全科學學報,2015,25(12).

[7]Pehlivan C,Augusto V,Xie X L.Dynamic Capacity Planning and Location of Hierarchical Service Networks Under Service Level Constraints[J].IEEE Transactions on Automation Science and Engineering,2014,11(3).

[8]Teixeira J C,Antunes A P.A Hierarchical Location Model for Public Facility Planning[J].European Journal of Operational Research,2008,185(1).

[9]Ratick S J,Osleeb J P,Hozumi D.Application and Extension of the Moore and ReVelle Hierarchical Maximal Covering Model[J].Socio-Economic Planning Sciences,2009,43(2).

[10]陳志芬,李強,陳晉.城市應急避難場所層次布局研究(Ⅱ)[J].自然災害學報,2010,19(5).

[11]Snyder L V,Daskin M S.Stochastic P-robust Location Problems[J].IIE Transactions,2006,38(11).

[12]馮春,于彧洋.不確定情景下應急物資儲備庫選址問題研究[J].工業工程,2014,17(2).

[13]李婷婷,宋瑞.國家層面綜合客運樞紐分層布局魯棒優化模型[J].東南大學學報：自然科學版,2015,45(1).

[14]萬波.公共服務設施選址問題研究[D].武漢：華中科技大學博士論文,2012.

[15]Berglund P G,Kwon C.Robust Facility Location Problem for Hazardous Waste Transportation[J].Networks&Spatial Economics,2014,(14).

[16]萬波,楊超,黃松,董鵬.基于層級模型的嵌套型公共設施選址問題研究[J].武漢理工大學學報：信息與管理工程版,2012,34(2).