基于預測區間理論的工程造價信息數據統計測算模型

李澤陽，劉 玲，胡奕仁

（1.武漢科技大學 管理學院，武漢430081；2.中國地質大學（武漢）工程學院，武漢 430074）

0 引言

“大數據”具有“5V”特征，即數據類別多（Variety）、數據體量巨大（Volume）、處理速度快（Velocity）、數據真實性（Veracity）、價值密度低、商業價值高（Value）[1]。工程造價信息包含政策法規、招投標信息、計價依據、價格信息、指數信息、指標信息、社會平均成本、社會平均利潤以及典型工程案例分析等，其具有大數據的特征，屬于大數據的范疇[2]。隨著對招標的建設工程實行“五價”備案制度，由建設項目的投資估算、設計概算、招標控制價、合同價、竣工結算等文件的書面及電子數據資料形成工程造價信息大數據[3-5]。

建安造價是工程造價構成中最基本、最重要的部分。可通過及時、真實地統計測算工程造價信息數據以快速、精準地計算新建工程的建安造價[6]。由于建安造價統計測算的影響因素多，變動幅度大[7]，所以目前工程造價主管部門發布的單位造價指標僅是對其均值的測算，未能對同地區、同類工程的單位造價取值區間及其概率做出精確的統計和測算[8]。本文運用統計學方法測算工程造價共享指標，及時、真實地隨機抽樣并處理工程造價信息數據，以貝葉斯學派思想為指導，并運用正態模型參數估計、卡方擬合檢驗、預測區間估計等方法[9-11]，測算出同地區、同類工程的單位造價區間及其概率，為測算新建工程的建安造價及建設投資提供指標和參數，為工程造價信息大數據的挖掘及應用提供一種科學、合理的統計測算方法[12-14]。

本文旨在運用統計學方法解決單位造價測算中存在的離散性、隨機性、不精確性等問題。首先，對原始數據進行預處理，降低時效性、區域性、工程類別等因素對測算結果的影響；然后，結合貝葉斯思想和相關經典統計學理論[9-11]，構建工程造價信息數據統計測算模型；最后，測算出單位造價的預測區間及其概率，以快速、精準地測算新建工程的建安造價及投資估算。

1 研究方法

點估計和區間估計為未知參數提供了很好的信息[10]。有時，相對于總體均值，人們對預測未來觀測值更感興趣。例如，在對工程造價信息數據統計測算研究中，需要利用觀測數據來預測一個新的觀測結果，即投資者對預測新建項目的工程造價更感興趣。估計工程造價的均值和置信區間，只能為新建項目工程造價測算提供一個大致的定位。投資者需要一個關于單個觀測的不確定性說明，而預測區間的建立可以滿足快速、精準地測算新建工程造價的要求。

假設隨機樣本是從未知均值、已知方差的正態總體里得到的[11]。新觀測結果的點估計值為,點估計值的方差為。在新觀測中隨機誤差的方差是σ2。由于新觀測值x0與樣本均值是獨立的，且預測方差是單一觀測隨機誤差的方差和估計均值的方差之和，所以可構造統計量如式（1）所示：

z服從n(z;0,1)。如果利用Z統計量的概率式（2），且將x0置于概率語句的中心，則式（3）成立。

2 工程造價信息數據統計測算模型構建

2.1 原始數據的處理

對同地區、同類工程的單位造價進行隨機抽樣。首先，取同地區、同類工程的單位造價的樣本數據，依據資金時間價值已知現值求終值的等值換算公式（5）[2]，將隨機抽樣的單位造價原始數據換算到同一時點。

處理后的單位造價記為x1,x2,…,xn；由于模型是通過樣本來研究總體，而總體可能出現任何情況，因此可以采用連續性修正，記頻率分布直方圖橫坐標的覆蓋區間為R；其次，對單位造價按大小排序并確定適當的組距，統計落在每個區間的樣本頻數fi，計算得出頻率；最后，以組距為橫坐標、以頻率為縱坐標繪制樣本分布頻率直方圖，觀測樣本數據近似來自于某種分布總體。

2.2 極大似然估計

隨機抽樣收集單位造價樣本觀察值，由于單位造價可看作類似于樣本均值的統計量，因此根據中心極限定理，繪制的樣本分布頻率直方圖最有可能類似正態分布。模型假設隨機樣本來自參數為μ，σ的正態總體，即同類工程的單位造價總體服從正態分布，記分布函數為F（x;μ，σ)。根據極大似然估計原理，X的概率密度函數為式（6），似然函數為式（7）[11]：

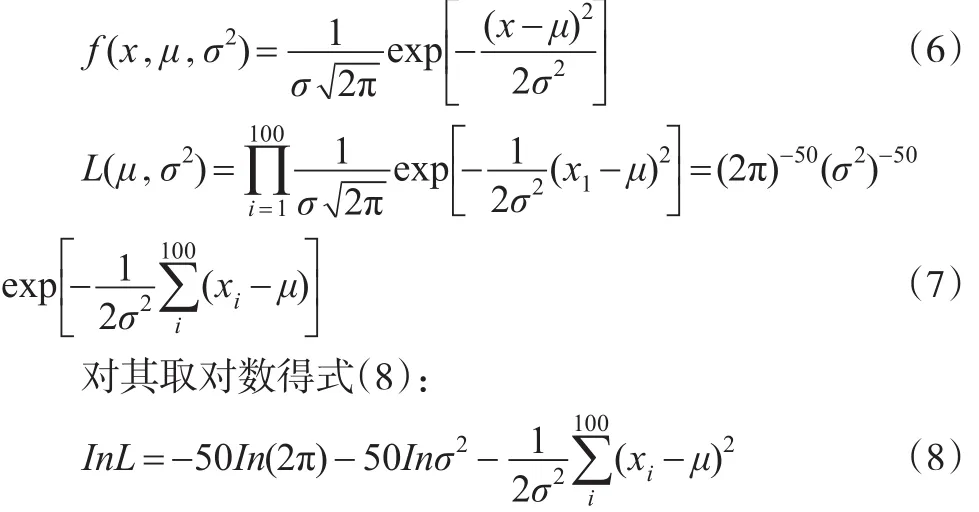
對其求偏導得式（9）：

式（10）即為同類工程的單位造價總體期望和方差的估計值。

2.3 卡方擬合檢驗

總體所屬分布類型的假設是依據觀測隨機樣本頻率分布圖得出，需要進一步檢驗，以上文計算得出的估計值作為參數值對分布類型進行擬合檢驗，檢驗其是否服從正態分布。設x服從正態分布，分布函數記作F(x;μ,σ)，將x取值的全體Ω劃分為k個互不相交的子集A1,A2,A3,…,An,將樣本觀察值x1,x2,x3,…,xn出現在Ai的個數記作2，3...k)，則事件＝Ai{x值在Ai內}的頻率為。計算事件的概率，得pi＝P(Ai)，i=1,2,3…,k。通常頻率與概率存在差異，當試驗次數足夠多時，這種差異將減少并可以忽略不計，即不應該太大，采用形如式（11）的統計量度量樣本與假設分布的擬合程度，其中Ci（在每一項前乘以適當的Ci，是為了使得統計量(11)有一個理想的極限分布）為常數。根據皮爾遜定理[10]，取，采用式（12）作為檢驗統計量。

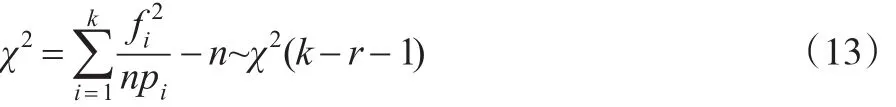
當X服從正態分布時，則式（13）成立。

此時χ2不應該太大，拒絕域為χ2≥G=χ2(k-r-1)。最后檢驗式（14）是否成立。

α為顯著性水平。不等式成立時拒絕原分布服從正態分布，否則就“不拒絕”原分布服從正態分布，即隨機樣本來自正態總體。

2.4 預測區間估計

檢驗隨機樣本正態性則可進行預測區間估計。在實際應用中，單位造價的總體期望和方差是未知的，總體期望和方差的估計值均為統計量，不是定值，若將估計值作為參數值直接導入統計量中進行預測區間估計則勢必會影響計算結果的精確度，造成系統誤差。當n較大時student分布與正態分布相似，統計測算模型用student分布取代正態分布，用s代替σ進行運算，根據預測區間估計理論構造新的統計量，如式（15）：

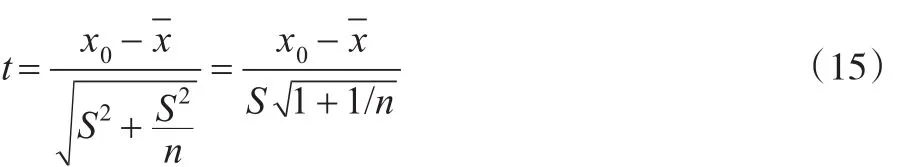
t服從自由度為n-1的student分布，運用T統計量的概率，見式（16）：

將x0置于概率語句的中心，式（17）所描述的事件發生的概率是1-α。

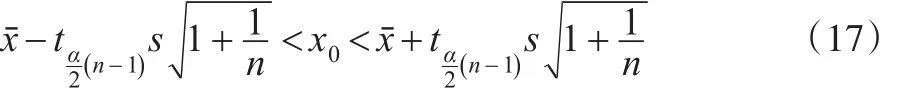
未來觀測x0的100（1-α）%的預測區間為式（18）：

3 實證

隨機抽樣收集某地區2013—2015年多層商品房住宅樓竣工結算的單位建安造價。如表1所示。

年折現率i取2012年末央行發布的貸款利率，即i=6.15%，將表1中2013年和2014年的單位造價，根據資金時間價值的等值換算方法，如公式（5），換算成同一時點的單位造價，整理數據如表2所示。

對數據進行統計與分析，多層商品房住宅樓單位建安造價在（0,1500）區間的頻率為2%，單位建安造價在（1500,1550）區間的頻率為7%，單位建安造價在（1550,1600）區間的頻率為16%，在（1600，1650）區間的頻率為47%，在（1650,1700）區間的頻率為21%，在（1700,1750）區間的頻率為5%，(1750,+∞)區間的頻率為2%，單位造價區間及頻率分布直方圖，如圖1所示。

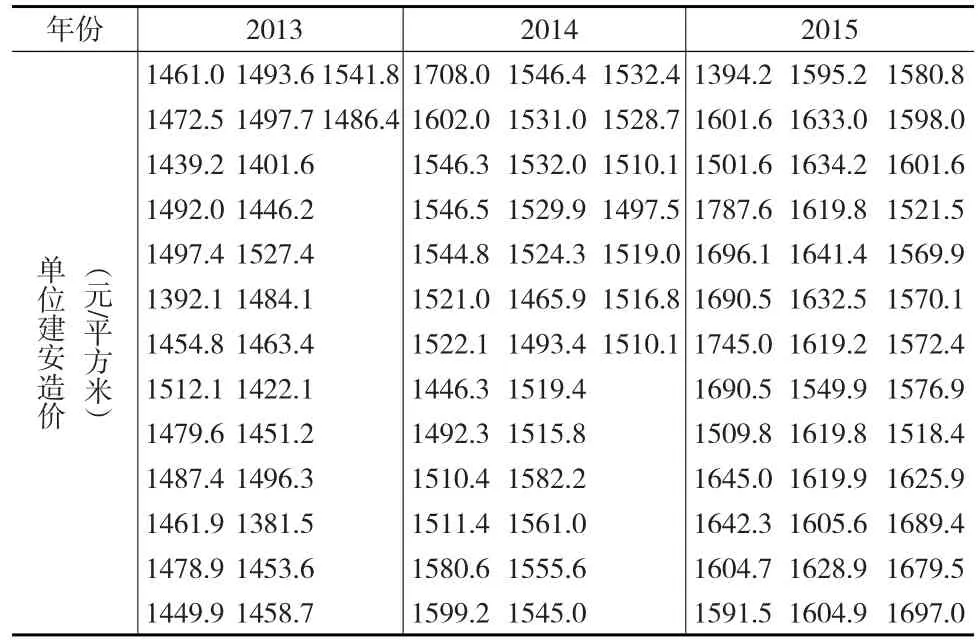
表1 某地區多層商品房住宅樓單位建安造價

表2 單位建安造價區間及頻率

圖1 某地區多層商品房住宅單位建安造價頻率分布圖

假設某地區單位造價符合參數為μ，σ的正態分布，記為X～N（μ,σ2）。設μ，σ為未知參數，x1,x2,… ,x100是來自X的樣本值，樣本均值為1626.3，樣本方差S2為3893.76，n為100，運用極大似然法估計法求得μ=1626.3，計算得出σ=62。以估計值作為參數值，計算時間Ai的概率，得pi=P(Ai)，pi與fi的計算結果，如表3所示。

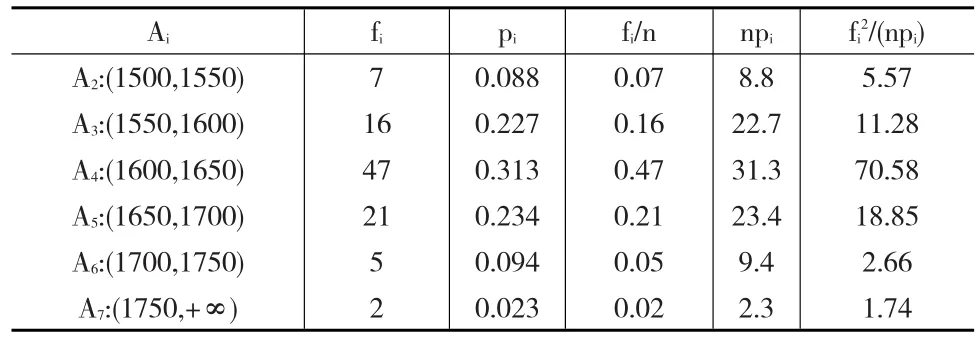
表3 卡方擬合檢驗的結果

由表3得x2＝112.58-100=12.58，依據卡方分布臨界值表可知：故在顯著性水平0.05下，可認為該組隨機樣本數據來自正態分布總體[15]。

根據所構建的預測區間估計模型，取顯著性水平α為0.05，統計測算單位造價區間為（1501.5，1751.0），隨機觀測結果在預測區間的概率為0.95，區間幅度為16.6%，單位造價在此區間內任意點均滿足建安造價測算的誤差要求。取顯著性水平為0.1時，預測區間為（1522.1，1730.5），隨機觀測結果在此預測區間的概率為0.90。同理，模型也可測算出不同顯著性水平下的單位造價預測區間。

一次隨機試驗發生的概率小于0.05即為小概率事件，通常認為小概率事件是不會發生的，即新建工程的單位建安造價一定在顯著性水平為0.05的預測區間范圍內。不同顯著性水平的單位造價預測區間可滿足不同建設工程對預測區間精準度的需求，為快速、準確地測算新建項目的工程造價和科學地投資決策提供模型方法和參數支持。

4 結論與討論

（1）本文構建了基于預測區間理論的工程造價信息數據統計測算模型，并通過實證研究測算出同類工程的單位造價預測區間及其概率，為測算新建同類工程的建安造價和投資估算提供指標和參數，也為全壽命周期工程造價主動管理提供模型和方法。

（2）模型對工程造價信息原始數據進行預處理，減少時效性、區域性、工程類別等因素對測算單位造價的影響，降低了隨機誤差。以貝葉斯學派思想為指導，將μ，σ等參數作為統計量，不直接使用其估計值，用樣本均值和樣本方差導入模型中運算，避免了系統誤差，提高了測算結果的精確度和可靠性。

（3）模型適用于工程造價信息數據的統計與測算，針對工程造價信息數據區域性和時效性的影響，采用指數調整或進行等值換算，將數據導入統計測算模型即可得測算結果。模型方法運算簡便，科學合理，精確度高，易于計算機編程，模型方法可廣泛應用于各種信息數據的統計、分析和測算。若后續研究抽取的樣本數量足夠大，并對處理原始數據的方法加以改進與完善，則模型測算結果會更精準，應用范圍也會更加廣泛。

參考文獻：

[1]陶雪嬌,胡曉峰,劉洋.大數據研究綜述[J].系統仿真學報,2013,(8).

[2]俞立平.大數據與大數據經濟學[J].中國軟科學,2013,（7）.

[3]沈祥華,姚甫昌,王紅兵.建筑工程概預算[M].武漢：武漢工業大學出版社,2008.

[4]馮斌,張建中.工程造價資料積累技術經濟分析指標體系設計及在Excel軟件環境下的應用[J].內蒙古工業大學學報,2005,(11).

[5]彭大敏,王罕.大數據環境下工程造價管理對策分析[J].建筑經濟,2014,(11).

[6]陳小龍,王立光.基于建筑設計參數分析模型的工程造價估算[J].同濟大學學報,2009,37(8).

[7]林琴.編制建設工程造價指標的探討[J].建筑經濟,2005,(2).

[8]吳學偉.住宅工程造價指標及指數研究[D].重慶：重慶大學碩士論文,2009.

[9]陳家鼎，鄭忠國.概率與統計[M].北京：北京大學出版社,2004.

[10]Navidi W.Statistics for Engineers and Scientists[M].China：Tsinghua University Press,2012.

[11]Ronald E.Walpole R H，Myers Sharon L.Probability and Statistics for Engineers and Scientists(Eighth Edition)[M].China：China Machine Pres,2010.

[12]Dong J,Wei FJ.A Study on Life Cycle-Oriented Analysis Method of Project Cost[J].The 1st International Conference on Information Science and Engineering，2009.

[13]董士波,鄭立新.全生命周期工程造價成本分析模型研究[J].9th Pacific Association of Quantity Surveyors Congress,2005.

[14]Dietterich T G,Michalski R S.Learning to Predict Seguences,Machine Learning[M].An Artificial Intelligence Ap-proach,1986.

[15]余建英，何旭宏.數據統計分析與SPSS應用[M].北京：人民郵電出版社,2003.