基于X13-A-S模型的中國食品價格指數研究

王斌會，史立新

（暨南大學 管理學院經濟管理實驗教學中心，廣州 510632）

0 引言

食品價格指數是居民消費價格指數(CPI)的重要組成部分，其波動直接影響居民生活水平和消費需求，與人們的日常生活和經濟社會穩定息息相關。由于人們的消費習慣和經濟波動等的影響，食品價格指數存在著顯著的季節性，沒有經過季節調整的食品價格指數數據往往很難掌握其波動規律。因此，通過季節調整對食品價格的預測及其規律的研究有著重要的理論價值和現實意義。

國際上目前在季節調整方面的最新成果是由西班牙銀行支持、美國普查局開發的X-13-ARIMA-SEATS（簡稱為X13-A-S），該程序在X-12-ARIMA最新版本的基礎上加入了TRAMO/SEATS季節調整程序，已廣泛應用于各國央行和研究機構的經濟分析過程。本文采用2001年1月至2015年9月我國食品價格指數月度定基數據，運用X13-A-S模型對其季節性波動規律進行研究，加入了我國最大的傳統節日春節。并對2015年10月至2016年9月的數據進行了預測。

1 原理與方法

1.1 X13-A-S基本原理

X13-A-S方法結合了X-12-ARIMA和SEATS兩種方法，在操作過程中可以選擇基于季節調整的SEATS模型和基于非參數調整的X-11模型。X13-A-S季節調整方法主要包含三個階段。①通過建立RegARIMA模型對原始序列中存在的各種離群值和歷法效應作預調整，然后對經過預調整后的序列進行向前預測和向后預測來補充數據；②反復嘗試運用不同長度的濾子SI對序列進行移動平均操作，從原序列中分離出各種成分（趨勢循環成分、季節成分和不規則成分等）；③對季節調整后的結果進行各種診斷檢驗。其流程如圖1所示。

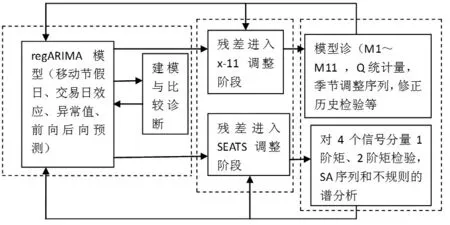
圖1 X13-A-S季節調整流程圖

RegARIMA模型是ARIMA模型與一般線性回歸模型的結合。對時間序列zt建立ARIMA模型：

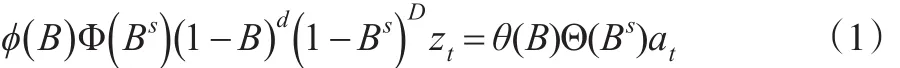
時間序列yt的線性回歸模型：

其中yt為因變量，xit為觀測變量，zt為回歸誤差項，滿足ARIMA模型。

聯立式（1）和式（2）得到RegARIMA模型：

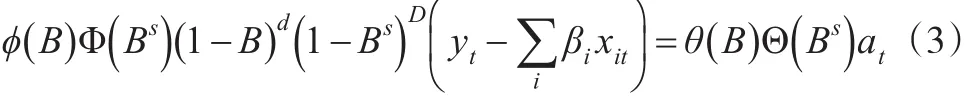
假設誤差項zt差分后得到穩定序列為wt，服從穩定的ARIMA模型，則ARIMA模型簡化為：

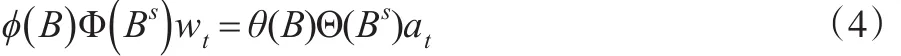
則RegARIMA模型可改寫為：

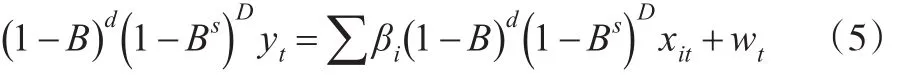
RegARIMA模型不僅繼承了X-11-ARIMA模型中補充首尾數據、延長時間序列的特性，還引入線性回歸對觀測數據的所有效應進行估計和檢驗。此外RegARIMA模型在X-12-ARIMA的基礎上擴大異常值檢驗和預調整的范圍，使時間序列季節調整更準確。

1.2 移動假日效應處理

移動假日是指定期出現但不一定對應著固定的公歷時間的節假日。例如我國的春節、清明節、中秋節和端午節。它們都對應著固定的農歷日期，但其每年所對應的公歷時間卻不是固定的。由于這類節假日的移動性，不能直接采用傳統的移動平均方法剔除其季節性，只能考慮在季節調整的RegARIMA建模階段引入節日回歸變量的方法來剔除其季節性。根據我國的實際情況，對食品價格影響最大的移動假日是春節。春節所帶來的消費高潮對食品價格指數影響顯著。越接近春節，人們會更積極地為即將到來的節日做準備，置辦年貨的活動會越來越頻繁，對食品價格指數的影響也會越來越明顯，此后人們的采辦活動隨著春節的過去而日漸減少直到最后節日影響消除。基于以上情況，擬采用以下方案在RegARIMA建模階段引入節日效應回歸變量：把春節對我國食品價格指數的影響分為兩個階段，第一個階段春節效應的影響每一天都是遞增的，第二個階段的影響每一天都是遞減的。這兩個階段形成“∧型”。若兩個階段的長度分別為n和m，本文設節前第n天的影響權重為1/n，節前第(n-1)天的影響權重為2/n，節前第(n-2)天的影響權重為3/n。以此類推，節前第1天的影響權重為n/n；節后第1天的影響權重為m/m，節后第2天的影響權重為(m-1)/m，同樣類推，節后第m天的影響權重為1/m。第i年j月所對應的影響權重就是當月的節日效應回歸變量的觀測值，其中不受春節效應影響的月份對應的權重為0。將計算出來的每月各天的影響權重加總后得到比例變量P(n)和P(m)，然后對P(n)和P(m)分別進行中心化處理，得到春節效應的節前和節后回歸變量，最后將其加入到regARIMA模型中進行估計，若對應的t檢驗無法通過，即表明該解釋變量影響不顯著，需對兩個階段的起止時期進行調整重新估計模型，不斷調整直到找到最佳的模型為止。

2 數據說明

根據最新公布的CPI構成和權重，我國CPI的商品構成中食品類商品所占的比例為33.6%,其決定著CPI運行的基本趨勢,本文選取我國2001年1月至2015年9月的食品價格指數為研究對象，而將2015年10月至2016年9月的數據用于預測對比，以檢驗模型的預測效果。數據以中華人民共和國統計局網站公布的為準。為了具有可比性，本文應選取食品價格指數的定基數據為研究對象，由于我國食品價格指數的定基數據難以獲取，所以采用固定一個時期為基期,通過對每年同月的同比指數連乘來計算定基比的方法對原始序列進行調整。本文對數據的調整是以2001年為基期,假設2001年各月食品價格指數初始值為100,通過2001年1月至2016年9月的月同比食品價格指數連乘計算得到這段時期的定基指數，如圖2所示。

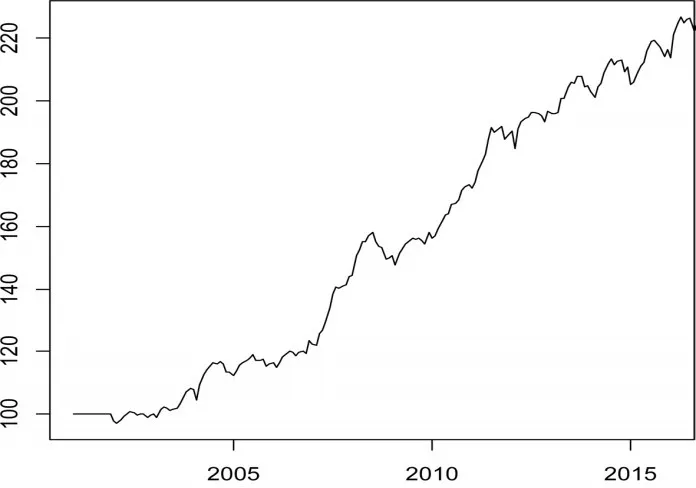
圖2 2001年1月至2016年9月我國食品價格指數定基時序圖

3 模型建立

3.1 模型初設

在季節調整之前，為了避免異方差性對模型造成影響，本文首先對食品價格指數求自然對數。

日歷效應設置包括：①交易日效應。即假設食品價格指數在周一至周五工作日之間存在差別，工作日與非工作日對食品價格指數波動存在影響。②閏年影響。主要表現在2月份長度對食品價格指數的影響。③移動假日效應。本文主要構建春節效應對食品價格指數的影響，考慮我國春節放假的實際情況，中國人一般習慣于從春節前10天左右開始采購年貨，在春節前2天的時候達到置辦年貨的最高峰，之后節日的影響一直持續，直到農歷正月十五元宵節后。本文將春節對食品價格指數的影響設置為“∧型”分布，第一階段設為節前10天到節前2天，即n=8。第二階段設為節前1天到正月十五元宵節結束，也就是m=16。第一段按照遞增的方式，第二段按照遞減的方式。將兩階段各天的影響權重加總后得到比例變量P(n)和P(m)，中心化后得到回歸變量pre_cny和post_cny，將這兩個自定義變量加入回歸方程進行估計。

異常值設置為選擇自動識別4種常見異常值以及季節性異常值。

3.2 模型結果及檢驗

確定日歷效應之后，建立模型，其檢驗結果見表1。

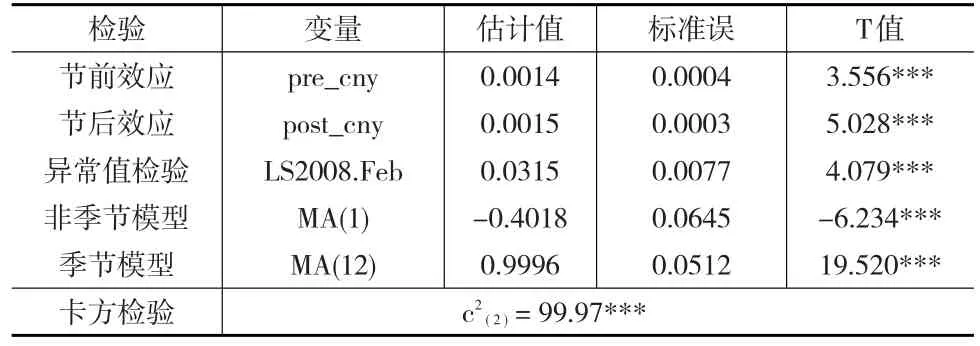
表1 我國食品價格指數季節調整模型檢驗結果

春節效應節前和節后估計值分別為0.0014、0.0015。由t統計量可以看出，春節效應變量pre_cny和post_cny具有很強的顯著性，表明食品價格指數受春節效應影響顯著，春節活動對食品價格指數有正向影響。對春節效應的兩個回歸因子進行卡方檢驗，檢驗兩個回歸因子的聯合顯著性。卡方檢驗的值為99.97，在0.1%的水平上是顯著的。交易日回歸和閏年效應計算表明，食品價格指數的交易日效應和閏年效應不顯著。因此，在分析建模過程中沒有進行交易日和閏年調整。異常值檢驗只檢驗出一個異常值，為2008年2月，異常值類型為水平移動。回歸系數為正值，T值為4.079，影響十分顯著。顯然食品價格指數受到2008年春節期間我國南方發生的罕見雨雪冰凍災害的影響。

接下來是建立ARIMA模型，經過識別和比較X13-A-S方法確定的模型為ARIMA(0,1,1)(0,1,1)，其表示序列經過一次季節差分和一次非季節差分后，為1階非季節移動平均項和一階季節移動平均平穩序列。ARIMA(0,1,1)(0,1,1)的DW統計量為1.98，殘差不存在自相關。

程序設計了11個M統計量和基于M的加權平均運算的Q統計量來檢驗季節調整的質量。M檢驗要求11個M統計量都小于1,Q檢驗則要求由11個M統計量采用不同權數組合加權得到Q值，越小越好。由表2可知，各統計量的值均小于1，因此模型質量較高。

表2 季節調整模型的M1～M11及Q統計量

我國食品價格指數的季節性檢驗結果如表3、表4所示：

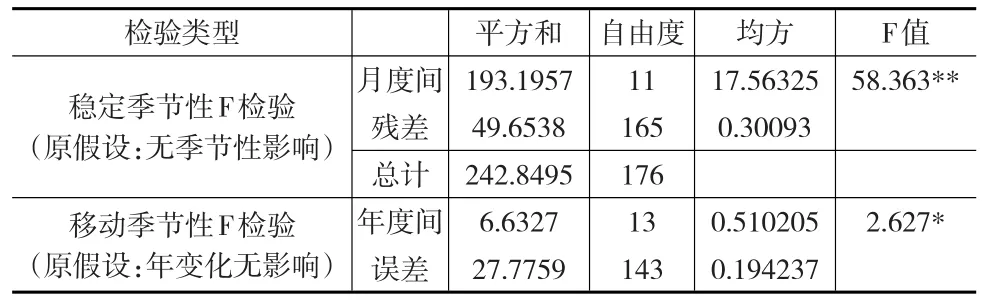
表3 食品價格指數季節性F檢驗

表4 食品價格指數季節性Kruskal-Wallis檢驗

X-11季節調整在估計季節因子時選取的是3×5季節移動濾波，在估計趨勢循環因子時使用9期Henderson趨勢濾波。兩個F檢驗和Kruskal-Wallis檢驗結果表明，在0.1%和1%顯著性水平下，食品價格指數中不僅存在穩定的季節性，還存在移動的季節性,即食品價格指數不僅隨月波動,還隨年波動。1%顯著性水平下接受了原假設，說明經過調整后的序列已經分離出了所有的季節性。

表5 食品價格指數殘差季節性檢驗

3.3 季節調整結果分析

季節調整的主要目標在于通過剔除季節成分，更加直觀地分析所選變量的內在規律和趨勢。模型通過檢驗之后，得到季節調整后的序列。圖3表示季節調整序列和原始序列的趨勢。從圖3可以看出原序列具有明顯的季節性，經過季節調整后序列總體上變得平滑。由季節調整序列可以看出，我國的食品價格指數大致可以分為兩個階段，第一階段：從2001年到2003年下半年，這一時期食品價格指數變化不大，說明期間的食品價格穩定，沒有大幅變化。第二階段：從2003年下半年到2015年，這幾年的食品價格指數呈現長期增長趨勢，其中2008年到2009年之間有短暫下滑，下滑原因則與全球金融危機有關。2008年的世界金融危機抑制了我國經濟增長，使得食品價格指數出現下降的趨勢。

圖3 食品價格指數及其季節調整序列時序圖

圖4為食品價格指數的季節因子和春節效應趨勢圖，容易看出分解出的季節因子的影響顯著不同于春節效應，季節性成分波動明顯，并且不同年份季節性強弱不同，季節性成分在2001年對食品價格指數影響較小，之后影響慢慢增強，2008年達到高峰，之后有所下降，此后幾年，季節性成分保持在一個比較穩定的程度，表明季節性成分對食品價格指數的影響比較穩定。就單個年份來看，在每年1月份左右，食品價格指數會呈現出一個高峰期。之后，人們對食品商品的需求會隨著節日氣氛的消退有所下降，進入全年的低谷期。接下來食品價格指數會在每年的7月份左右又呈現第二個高峰期，隨后又會下降。春節效應主要是春節節日消費因素的影響，春節效應會使食品需求量增加，帶動價格上漲，從而導致食品價格指數上升。春節的影響基本集中在1、2、3月份，對其他月份沒有影響。

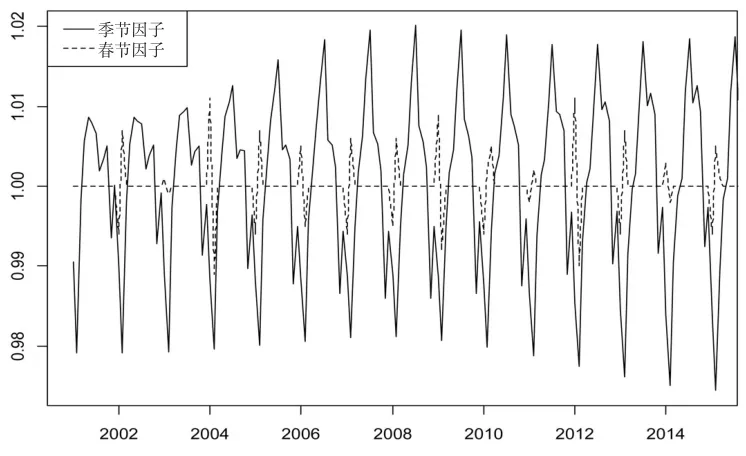
圖4 食品價格指數的季節因子和春節因子

4 模型預測

對食品價格指數的同比數據進行處理后，得到定基比數據，然后運用本文中考慮春節效應的X13-A-S方法進行季節性調整，最后得到的調整效果是令人滿意的，運用該方法對我國2015年10月至2016年9月的食品價格指數進行預測，得到的結果如表6所示，并把實際數據與預測結果進行對比，得出相對誤差。

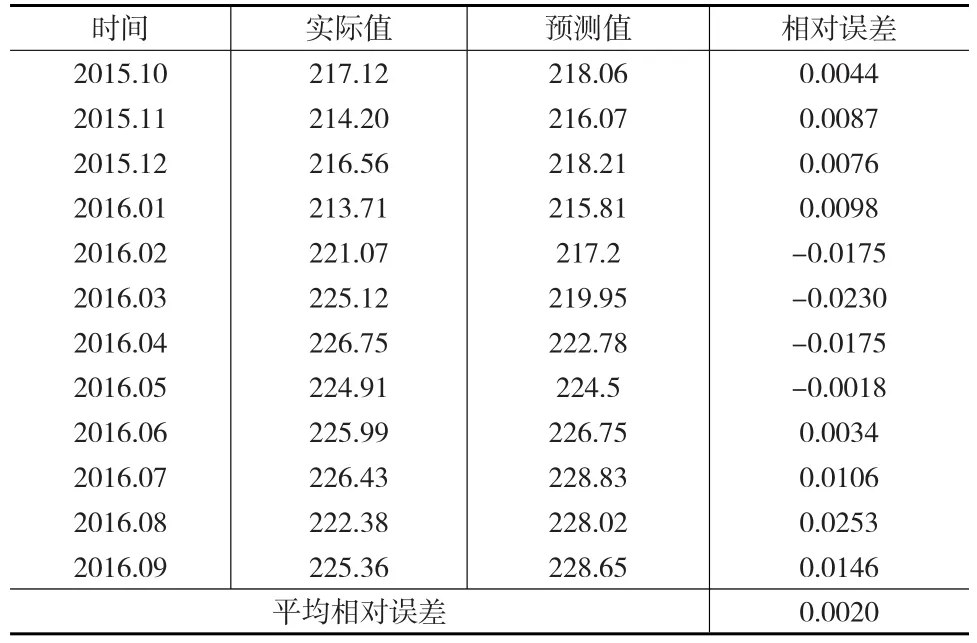
表6 食品價格指數預測值與實際值對比表

從表6可以看出，運用X13-A-S對我國食品價格指數月度數據的預測結果與真實值相差很小，模型的相對誤差非常小，進一步說明季節調整的效果令人滿意。

5 結論

本文根據2001年1月至2016年9月、以2001年為基期的食品價格指數數據，使用最新的X13-A-S方法對其進行季節調整，考慮了我國特有的移動假日春節，模型顯示春節的節前和節后效應都很顯著，而且對食品價格指數有正向作用；檢測的異常值只有1個，為2008年2月；確立模型為(0，1，1)(0，1，1)季節調整模型，通過季節性檢驗和殘差季節性檢驗，其不僅存在穩定的季節性，還存在移動的季節性；M1～M11、Q統計量都小于1，構建的模型較合理。最后使用本文的模型對2015年10月至2016年9月的食品價格指數進行預測，預測值與實際值非常接近，能夠很好地預測我國食品價格指數的走向。

參考文獻：

[1]Bell W R,Hillmer S C.Issues Involved With the Seasonal Adjustment of Economic Time Series[J].Journal of Business and Economic Statistics，1984，（92）.

[2]Findley D F，Monsell B C，Bell W R，et al.New Capabilities and Methods of the X-12-ARIMA Seasonal Adjustment Program[J].Journal of Business and Economic Statistics，1998，（2）.

[3]陳雄強等.貨幣供應量的實時監測——基于季節調整方法[J].上海經濟研究，2011，（7）.

[4]李靜等.我國食品價格變動的屬性特征——基于1996—2010年季度數據的實證分析[J].政府經濟管理，2011，（9）.