二值選擇模型內生性檢驗方法、步驟及Stata應用

袁 微

（上海財經大學 商學院，上海 200433）

0 引言

利用二值選擇模型進行實證研究，有時會遇到解釋變量為內生變量的情形。例如，考察幸福感影響慈善捐贈行為（捐贈/不捐贈）時，幸福感或許為內生變量。其原因是幸福感和慈善捐贈行為存在反向因果關系。具體來講，一方面，個體幸福感顯著正向影響個體慈善捐贈行為[1]；另一方面，個體慈善捐贈行為的發生又顯著提升個體幸福感[2]。幸福感是內生變量，在實證檢驗中使用通常的二值選擇模型將有可能得不到一致估計[3]。對此，要緩解或解決此問題就有必要進行內生性檢驗。

縱觀國內外有關內生性檢驗的文獻，雖然有提及OLS模型內生性檢驗方法、步驟及Stata應用[4-6]，但是卻鮮少提及二值選擇模型內生性檢驗的具體方法、步驟及Stata應用。即使陳強（2014）[6]曾在著作中將二值選擇模型中的Probit模型內生性檢驗作為“選讀”章節，但是其卻并未對此問題進行深入探討。正如以上原因，使得眾多學者，尤其是初學者在進行二值選擇模型內生性檢驗時心存眾多疑問。例如，（1）相對于OLS模型內生性檢驗，二值選擇模型內生性檢驗的具體方法、步驟和Stata應用是什么？（2）對于二值選擇模型中含有的內生變量數量的變化，則又該如何處理？（3）對于二值選擇模型中存在內生變量與其他解釋變量交互的情況，則又該如何處理？以上這些問題均是學者們在進行二值選擇模型內生性檢驗時可能會遇到的問題。因此，本文將以二值選擇模型中的Probit模型為例，根據陳強（2014）[6]提出的Probit模型內生性檢驗原理，圍繞以上問題展開研究，以期能解開學者和初學者們在進行二值選擇模型內生性檢驗時所遇到的困惑。

1 Probit模型內生性檢驗的方法及原理

“工具變量 Probit”（Instrumental Variable Probit，簡稱IV Probit）和“兩步法”（Two-step Method）是學術界公認的兩種檢驗Probit模型內生性的有效方法[7-9]。目前，有眾多學者已對以上兩種方法的原理進行了詳細介紹。本文主要基于已有文獻提出的原理，針對學者們在研究中對Probit模型內生性檢驗的若干疑問進行闡釋。本文將陳強（2014）[6]對Probit模型內生性檢驗的方法及相關原理的介紹如下：

其中，y1i為可觀測的虛擬變量，y*1i為不可觀測的潛變量，y2i是模型中唯一的內生變量。方程（1）稱為“結構方程”（該方程右邊含內生變量），而方程（2）稱為“第一階段方程”或“簡化式方程”（該方程右邊不含內生變量）。

其中，ui的方差被標準化為1，而ρ為的相關系數。顯然，由于υi服從正態分布，故y2i也服從正態分布，因此y2i必須為連續變量。進一步，假設獨立于xi與zi，故在方程（1）中，xi為外生解釋變量。而且，zi可作為方程（1）中內生變量y2i的工具變量，因為zi與內生變量y2i相關，且zi與ui無關。在此模型中，y2i的內生性完全來自于ui與υi的相關性；如果二者的相關系數ρ=0，則y2i為外生變量。因此，對于y2i內生性的檢驗可以通過檢驗“H0:ρ=0”來進行。

由方程（1）至方程（4）所構成的模型，在給定xi與zi的情況下，的條件概率分布已經完全確定。將聯合概率密分解為zi)，可寫出樣本數據( )y1i,y2i的似然函數，然后進行最有效率的MLE估計。此方法稱為“工具變量Probit”。

盡管MLE最有效率，但在數值計算時，可能不易收斂，特別在多個內生解釋變量的情形下。可以使用兩步法。基本思想如下：

在方程（1）中，既然y2i的內生性是由于遺漏了變量υi所造成，那么如果能把υi作為控制變量放入方程（1）即可得到一致估計。雖然方程（2）的擾動項υi不可觀測，但可用OLS殘差作為υi的一致估計。

由于( )ui,υi服從二維正態分布，故根據多元統計知識，ui對于υi的總體回歸方程可以寫為：

其中，Vаr()ui=1。將方程（5）代入方程（1）可得：

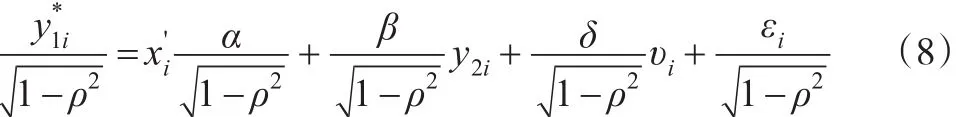
由于方程（8）中的υi不可觀測，故兩步法由以下兩步構成：

第一步：對簡化式方程（2）進行OLS回歸，得到殘差。

第二步：以殘差替代方程（8）中的υi，進行Probit估計，得到對變換后系數的估計。

在使用兩步法的情況下，對y2i內生性的檢驗可通過檢驗原假設“H0:δ=0 ”來進行，如果δ=0 ，則ui與υi不相關。

綜合以上所述可知，Probit模型內生性檢驗的方法主要有MLE和兩步法兩種，但是鑒于兩步法比MLE計算方便且適合在多個內生解釋變量的情形下使用，所以本文將基于兩步法來闡述Probit模型內生性檢驗的具體步驟及Stata應用。

2 不同情況下Probit模型內生性檢驗的步驟及Stata應用

2.1 只含有單個內生解釋變量

其中，y為被解釋變量，x1為內生解釋變量；x2…xn為控制變量；β0、β1、β2…βn為待估計的系數；εi為隨機擾動項。本文假設z1和z2為內生解釋變量x1的工具變量，則可根據以下步驟進行Probit模型內生性檢驗。

2.1.1 初始工具變量檢驗

對于所選擇的工具變量，首先需要進行初步檢測，即檢測工具變量z1和z2的有效性以及判斷x1是否為內生解釋變量。初始工具變量的檢驗的原假設為“H0：內生變量為外生”；備選假設為“H1：內生變量為內生”。初始工具變量的檢驗應該拒絕原假設，不拒絕備選假設。

初始工具變量檢驗的Stata命令：

2.1.2 過度識別檢驗

若模型中含有的內生解釋變量個數等于或少于工具變量個數，則無需進行過度識別檢驗；反之，則需要進行過度識別檢驗[3]。所謂的過度識別檢驗自身為一種卡方檢驗，它是對所選取的工具變量進一步的檢測，以確認所選擇的工具變量均為外生，即與擾動項不相關。它的原假設為“H0：所有工具變量均為外生”；備選假設為“H1：至少存在一個工具變量為內生”。過度識別檢驗應該不拒絕原假設，拒絕備選假設。鑒于模型（9）中所含有的內生解釋變量（x1）個數少于所選取的工具變量（z1和z2）個數，所以需要進行過度識別檢驗。

過度識別檢驗的Stata命令：overid

2.1.3 弱工具變量檢驗

弱工具判斷也叫考察工具的相關性。檢驗內生變量和工具變量的相關性，也就是檢驗模型的回歸系數的極限分布是否是正態分布，是否會扭曲相應統計量的一致性[10]。弱工具變量檢驗的原假設為“H0：內生變量與工具變量不相關”；備選假設為“H1：內生變量與工具變量相關”。弱工具識別檢驗應該拒絕原假設，不拒絕備選假設。

弱工具識別檢驗的Stata命令：

值得注意的是，ivprobit與OLS模型在內生性檢驗步驟上的區別是：OLS模型經過以上三種檢驗之后，還需要進行最后一步檢驗——Durbin-Wu Hausman檢驗，即外生性檢驗，用以檢測IV模型是否優于OLS模型。但是ivprobit模型則不需要再進行Durbin-Wu Hausman檢驗，其原因是ivprobit已經在上述三種檢驗中提供了內生性檢驗（H0：內生變量為外生，及rho＝0）[6]。

綜合以上可知，完整的Probit模型內生性檢驗主要包括三個步驟：初始工具變量檢驗、過度識別檢驗和弱工具識別檢驗。若模型中含有的內生解釋變量個數多于所選取工具變量個數，則需要進行過度識別檢驗；反之，則不需要進行過度識別檢驗。

鑒于處于不同情況下的Probit模型內生性檢驗的方法、原理及步驟并無顯著差異，因此本文將直接書寫相應的Stata命令。

2.2 含有多個內生解釋變量

其中，y為被解釋變量，x1、x2、x3為內生解釋變量；x4,…,xn為控制變量；β0、β1、β2、β3、β4…βn為待估計的系數；εi為隨機擾動項。本文假設z1、z2和z3分別為內生解釋變量x1、x2和x3的工具變量，則可根據以下步驟進行Probit模型內生性檢驗。

2.2.1 初始工具變量檢驗

初始工具變量檢驗的Stata命令：

ivprobity x4…xn（x1x2x3=z1z2z3）,first twostep

2.2.2 過度識別檢驗

由于模型（10）中含有的內生解釋變量（x1、x2和x3）個數等于所選取的工具變量（z1、z2和z3）個數，則無需進行過度識別檢驗。

2.2.3 弱工具變量檢驗

弱工具識別檢驗的Stata命令：

weakiv ivprobityx4…xn（x1x2x3=z1z2z3）,twostep

2.3 含有單個內生解釋變量，且該變量與其他解釋變量存在交互項

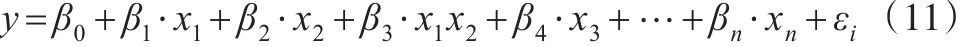
其中，y為被解釋變量，x1為內生解釋變量；x2為外生解釋變量；x1x2為內生解釋變量x1和外生解釋變量x2的交互項；x3,…,xn為控制變量；β0、β1、β2、β3、β4…βn為待估計的系數；εi為隨機擾動項。本文假設z1和z2為內生解釋變量x1的工具變量，則可根據以下步驟進行Probit模型內生性檢驗。

2.3.1 初始工具變量檢驗

模型（11）中x1x2是內生解釋變量x1和外生解釋變量x2的交互項，因為x1是內生解釋變量，所以交互項x1x2也是內生解釋變量。在進行初始工具變量檢驗之前，針對交互項x1x2，需要先分別生成工具變量z1和z2與外生解釋變量x2的交互項z1x2和z2x2。其相應的Stata命令為：genz1x2＝z1*x2；genz2x2＝z2*x2。完成以上操作，便可進行初始工具變量檢驗。

初始工具變量檢驗Stata命令：

ivprobityx2x3…xn（x1x1x2=z1z2z1x2z2x2）,first twostep

2.3.2 過度識別檢驗

由于模型（11）中含有的內生解釋變量（x1和x1x2）個數少于所選取的工具變量（z1、z2、z1x2和z2x2）個數，所以需要進行過度識別檢驗。

過度識別檢驗的Stata命令：overid

2.3.3 弱工具變量檢驗

弱工具識別檢驗的Stata命令：

weakiv ivprobityx2x3…xn(x1x1x2=z1z2z1x2z2x2),twostep

2.4 含有多個內生解釋變量，且這些變量與其他解釋變量存在交互項

其中，y為被解釋變量，x1、x3為內生解釋變量；x2、x4為外生解釋變量；x1x2為內生解釋變量x1和外生解釋變量x2的交互項；x3x4為內生解釋變量x3和外生解釋變量x4的交互項；x5,…,xn為控制變量；β0、β1、β2、β3、β4…βn為待估計的系數；εi為隨機擾動項。本文假設z1和z2分別為內生解釋變量x1、x3的工具變量，則可根據以下步驟進行Probit模型內生性檢驗。

2.4.1 初始工具變量檢驗

根據前文的介紹，在進行初始工具變量檢驗之前，針對交互項x1x2和x3x4，需要先生成工具變量z1與外生解釋變量x2的交互項z1x2，以及工具變量z2與外生解釋變量x4的交互項z2x4。其相應的Stata命令為：genz1x2＝z1*x2；genz2x4＝z2*x4。完成以上操作，便可進行初始工具變量檢驗。

初始工具變量檢驗的Stata命令：

ivprobityx2x4…xn(x1x3x1x2x3x4=z1z2z1x2z2x4),first twostep

2.4.2 過度識別檢驗

由于模型（12）中含有的內生解釋變量（x1、x3、x1x2和x3x4）個數等于所選取的工具變量（z1、z2、z1x2和z2x4）個數，所以不需要進行過度識別檢驗。

2.4.3 弱工具變量檢驗

弱工具識別檢驗的Stata命令：

weakiv ivprobityx2x4…xn(x1x3x1x2x3x4=z1z2z1x2z2x4),first twostep

3 實例分析

3.1 模型和數據

3.1.1 模型設定

模型（13）為Probit模型，其中Happinessi是被解釋變量，用來衡量家庭i是否幸福的指標；解釋變量中，變量Donatei是衡量家庭i慈善捐贈額的指標；Fmbi為啞變量，表示家庭i的成員數水平；變量Wi是影響家庭幸福感的家庭特征變量矩陣，如Inc、Hel、Emp；變量Zi是影響家庭幸福感的宏觀經濟安全環境變量矩陣，如Pse、Fey；Dcmi表示城市虛擬變量；β0、β1、δ0、δ1、Γ 、Π 和γ1分別為待估計的系數或系數向量；εi為隨機擾動項（變量定義見表1）。

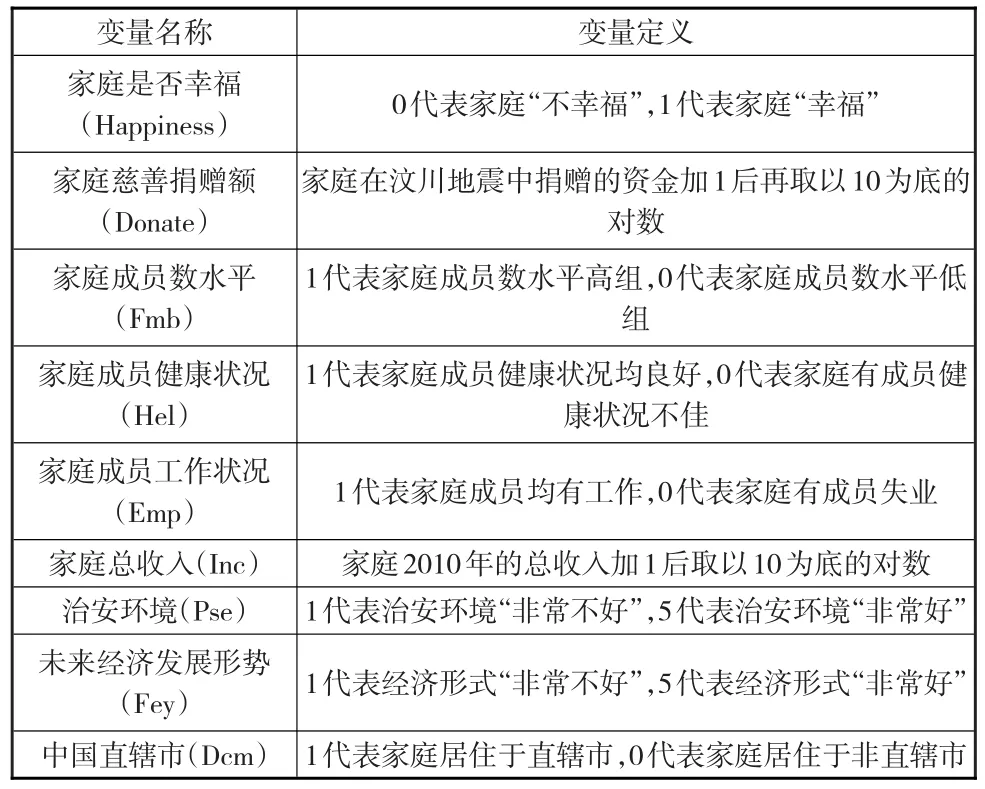
表1 變量定義

3.1.2 數據描述

本文采用的數據均來自于2011年的《中國家庭金融調查》（China Household Finance Survey,CHFS）。CHFS（2011）是西南財經大學中國家庭金融調查與研究中心進行的一項全國性的調查，以隨機抽樣的方法訪問被調查者，被調查者的足跡遍布全國25個省、80個縣、320個社區，完成樣本8438份。

在剔除了數據缺失的樣本之后，本文最終整理得到了3013份微觀樣本。這3013份樣本分別分布在中國東部城市（9個）、中部地區（8個）、西部地區（8個）。從表2的樣本城市地理分布來看，其分布較為平均，說明本文所研究的樣本具有一般的代表性。

表2 樣本城市分布表

3.2 回歸分析與內生性檢驗

3.2.1 回歸分析

在進行一般的Probit模型回歸之前，首先需要生成解釋變量Donate與解釋變量Fmb的交互項Donate_Fmb，其相應的Stata命令為：

gen Donate_Fmb=Donate*Fmb

完成以上操作，則可進行一般的Probit模型回歸，其相應的Stata命令為：

probit Happiness Donate Fmb Donate_Fmb Hel Emp Inc Pse Fey Dcm

一般的Probit模型回歸結果見表3。

表3 一般的Probit模型回歸結果

表3顯示，Donate的系數為0.128，且在1%水平上顯著，即家庭慈善捐贈額越高，則家庭越幸福。Donate_Fmb的系數為0.093，且在5%水平上顯著，即在其他條件保持不變的情況下，家庭成員數水平高的家庭與家庭成員數水平低的家庭所捐贈的金額一致時，則家庭成員數水平高的家庭可能比家庭成員數水平低的家庭更幸福。但本文認為Donate不是內生解釋變量，因為家庭慈善捐贈與家庭是否幸福之間可能存在反向的因果關系，即家庭是否幸福也影響了家庭慈善捐贈。具體來說，感到幸福的家庭在親社會行為方面表現得更為積極（如頻繁捐贈，捐款金額較多），而幫助他人本身又能提高家庭的幸福感。由于家庭慈善捐贈和家庭是否幸福這兩者之間可能存在反向的因果關系，所以這將會使得家庭慈善捐贈是家庭是否幸福決定方程中的內生解釋變量。此時，一般的Probit模型計算得到的回歸系數就不具有一致性。為此，基于此情況就需要對Probit模型進行內生性檢驗。

3.2.2 內生性檢驗

（1）初始工具變量檢驗

本文將Hgen（戶主的性別，1代表男性，0代表女性）、Hpmr（戶主的政治身份，1代表黨員，0代表非黨員）、Hedu（戶主的教育水平，1代表高教育水平，0代表低教育水平）作為內生解釋變量Donate的工具變量。一方面，戶主性別、政治身份與教育水平與家庭慈善捐贈額Donate相關，滿足工具變量的相關性；另一方面，假設戶主的性別、政治身份與教育水平不直接影響家庭的幸福，故滿足工具變量的外生性。在使用這些工具變量進行IV Probit估計之前，依然需要先分別生成戶主性別Hgen、政治身份Hpmr、教育水平Hedu與外生解釋變量Fmb的交互項Hgen_Fmb、Hpmr_Fmb和Hedu_Fmb，其相應的Stata命令為：

gen Hgen_Fmb=Hgen*Fmb

gen Hpmr_Fmb=Hpmr*Fmb

gen Hedu_Fmb=Hedu*Fmb

完成以上步驟，方可進行IV Probit估計，其相應的Stata命令為：

ivprobit Happiness Fmb Hel Emp Inc Pse Fey Dcm（DonateDonate_Fmb= HgenHpmrHeduHgen_FmbHpmr_Fmb Hedu_Fmb），first twostep

IV Probit估計的結果見表4至表6。

表4 IV Probit估計第一階段回歸結果I

表5 IV Probit估計第一階段回歸結果II

表6 IV Probit估計第二階段回歸結果

表6提供了對外生性原假設“H0:ρ=0”的沃爾德檢驗結果，其p值為0.0006，故可在1%的水平上認為Donate和Donate_Fem為內生解釋變量。根據表3的估計結果可知，Donate變量的系數為0.128，在1%的水平上顯著；Fem變量的系數為-0.282，在1%的水平上顯著；Donate_Fem變量的系數為0.938，在10%的水平上顯著；Hel變量的系數為0.53，在10%的水平上不顯著。但是表6的IV Probit估計結果顯示，Donate變量的系數為0.215，在5%的水平上顯著；Fem變量的系數為-0.104，在1%的水平上顯著；Donate_Fem變量的系數為0.505，在1%的水平上顯著；Hel變量的系數為0.138，在10%的水平上顯著。以上結果表明，如果使用一般的Probit模型進行估計，由于忽略了Donate的內生性，將低估家庭慈善捐贈額對家庭幸福的正作用；將高估家庭成員數水平對家庭幸福的負作用；將高估家庭慈善捐贈與家庭成員數水平的交互項對家庭幸福的正作用；將忽略家庭成員健康狀況對家庭幸福的正作用。另外，從表4的回歸結果來看，工具變量Hgen、Hpmr、Hedu對于內生變量Donate具有較強的解釋力；從表5的回歸結果來看，工具變量Donate_Hgen、Donate_Hpmr、Donate_Hedu對于內生變量Donate_Fmb具有較強的解釋力。

（2）過度識別檢驗

由于模型（13）中含有的內生解釋變量（Donate、Donate_Fem）個數少于所選取的工具變量（Hgen、Hpmr、Hedu、Hgen_Fmb、Hpmr_Fmb、Hedu_Fmb）個數，所以需要進行過度識別檢驗以進一步檢測選取的工具變量。

過度識別檢驗的Stata命令為：overid

過度識別檢驗結果中的p值為0.3870，其小于0.05，則不拒絕原假設“H0:所有工具變量均為外生”，這說明本文所選取的工具變量都是外生變量。

（3）弱工具識別檢驗

弱工具識別檢驗的Stata命令為：

Weakiv ivprobit Happiness Fmb Hel Emp Inc Pse Fey Dcm（Donate Donate_Fmb=Hgen Hpmr Hedu Hgen_Fmb Hpmr_Fmb Hedu_Fmb），twostep

弱工具識別檢驗的結果見表7。

表7 弱工具識別檢驗結果

表7結果顯示，CLR、K-J、AR、Wald的p值均在1%水平上顯著，則應該拒絕原假設“H0：內生變量與工具變量不相關”，不拒絕備選假設“H1：內生變量與工具變量相關”。這也說明，本文所選擇的工具變量不是弱工具變量。

4 總結

本文基于學者們在二值選擇模型內生性檢驗方面積累的研究成果，以Probit模型為例，對二值選擇模型內生性檢驗的具體方法、步驟和Stata應用進行了拓展。例如，本文提出完整的Probit模型內生性檢驗由三大步驟組成：初始工具變量檢驗、過度識別檢驗和弱工具識別檢驗，而后兩個步驟前輩們并未指出。另外，本文給出了處于不同情況下的Probit模型內生性檢驗方法及Stata應用。

參考文獻：

[1]南方,羅微.社會資本視角下城市居民捐款行為的影響因素分析[J].北京師范大學學報：社會科學版,2013,(3).

[2]唐聞捷.民營企業家慈善捐贈行為與主觀幸福感——基于溫州地區中小型民營企業家的調查[J].浙江社會科學,2013,(8).

[3][美]伍德里奇.計量經濟學導論（第四版）[M].北京：中國人民大學出版社,2010.

[4]倪偉才.兩種內生性檢驗方法的等價性[J].科技視界,2012，(29).

[5]王美今,林建浩,胡毅.IV估計框架下模型設定檢驗問題的討論[J].統計研究,2012,(2).

[6]陳強.高級計量經濟學及Stata應用（第二版）[M].北京：高等教育出版社,2014.

[7]Newey W K.Efficient Estimation of Limited Dependent Variable Models with Endogenous Explanatory Variables[J].Journal of Econometrics,1987,36(3).

[8]Rivers D,Vuong Q H.Limited information Estimators and Exogeneity tests for Simultaneous Probit Models[J].Journal of econometrics,1988,39(3).

[9]周廣肅,梁榮,田金秀等.Stata統計分析與應用[M].上海：機械工業出版社,2011.

[10]Pflueger C E,Wang S,Newton H J,et al.A Robust Test for Weak Instruments in Stata[J].Social Science Electronic Publishing,2015,31(3).