基于貝葉斯Lasso處理異常值及重尾數據的研究

王新軍，朱永忠，李佳蓓

（河海大學 理學院，南京 211100）

0 引言

考慮普通最小二乘回歸問題：

其中y為解釋變量，y∈Rn，X為回歸矩陣，X∈Rn×p，其中p為預測變量數，n為樣本觀測數，‖?‖2是Rn中的歐幾里得空間并且β∈Θ?Rn。為了更好地提出問題，假設p＜n，XTX非奇異，對于上述問題，普通最小二乘估計（OLS）是最常見的解決方法。然而，在高維問題中，普通最小二乘估計很難處理，一些微小的變化可能導致估計不穩定。比如，觀測數據的微小變化就可能導致參數估計的極端變化。

1996年，Tibshirani提出了Lasso估計[1]，其本質是通過L1懲罰對模型系數進行壓縮，將沒有影響或影響較小的自變量的回歸系數自動壓縮到零，從而不僅在一定程度上能消除多重共線性的影響，而且在對參數進行估計的同時也實現了對變量的選擇。

對于如下有約束的最優化問題：

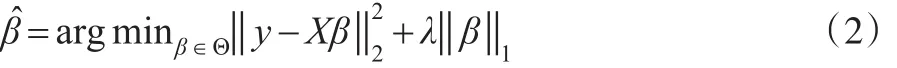
Lasso估計以方差小幅度的降低來換取偏差的少量增加，從而使得均方誤差整體上降低。Lasso估計不僅避免了普通最小二乘估計在高維問題中的不穩定性，而且能夠達到變量選擇的目的。然而Lasso引進的L1懲罰函數不可微[2]，從而導致估計的協方差陣不存在緊集，對于此問題，需要采用重采樣方法解決。

2008年，Park T和Casella G提出了Bayesian Lasso方法(BLasso)[3]，在貝葉斯理論框架下，對回歸系數引進如下的獨立Laplace條件先驗：

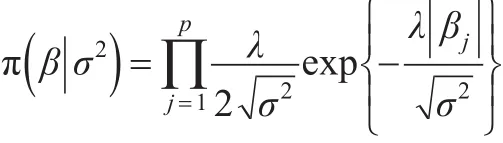
發現其邊際后驗眾數與Lasso給出的估計一致，彌補了Lasso的不足。上述σ2的分布如果不合適會導致最優化求解有多個滿足條件的估計值，而不是唯一的，因此σ2的后驗分布必須是單峰的。BLasso法避免了采用重抽樣方法對協方差陣估計，然而，其未解決正態誤差項在極大似然假設下的穩健性。

在很多情況下（基因組學、計量經濟學、金融數據等）經常會遇到數據中存在異常值或者當數據不是服從正態分布假設，而是服從重尾分布。在這些情況下，回歸系數的估計很有可能受到影響，使得模型預測精度受到影響。

為此，本文改進BLasso方法，在BLasso的基礎之上引入兩組潛變量，這樣做的優勢在于：一是允許模型存在誤差或者異常值，能夠模擬出常見的偏態和重尾分布，從而能夠確保模型的穩健性，二是保持模型的共軛性，能夠更好地應用Gibbs抽樣。在引進潛變量之后，利用邊緣極大似然估計方法，對潛變量邊際優化，從而得出未知參數的極大似然函數。本文選用層次模型的誤差項是逆伽馬正態混合分布的尺度參數，這與BLasso層次模型采用的服從t分布的誤差項相類似[4]，但是選用了不同的層次模型以及懲罰函數結構，從而能夠在已知參數的似然Laplace先驗分布的情況下實現更加穩健的Gibbs抽樣。通過數據仿真發現，當數據中出現異常值，或者數據服從重尾分布的情況下能夠給出相比Lasso，BLasso更加精確的估計以及較好的變量選擇。

1 模型及方法

1.1 分層模型

為了使估計過程更穩健，考慮如下回歸問題，并假設貝葉斯方法是其解決方法：

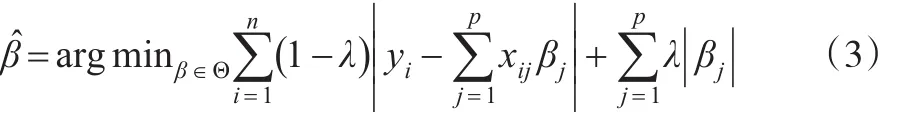
上述最優化問題通過引入懲罰系數λ對損失函數L1以及回歸系數懲罰，其中λ∈[ ]0,1。之所以在損失函數L1中加入懲罰項，是考慮到保持模型預測和數據壓縮之間的平衡，從而獲得較好的穩健估計。當λ=0時，；當λ=1時，

通過邊際似然方法，在假設兩組超參數以及懲罰參數的先驗分布為Laplace先驗分布的情況下，得到服從邊際似然Laplace先驗分布的重尾數據，利用貝葉斯理論得到各參數的后驗分布，將這種方法稱之為平衡的貝葉斯Lasso（BBLasso）。

首先，為了給每一個參數構建一個具有封閉形式的條件后驗分布，所有參數采用如下的全條件分層結構：

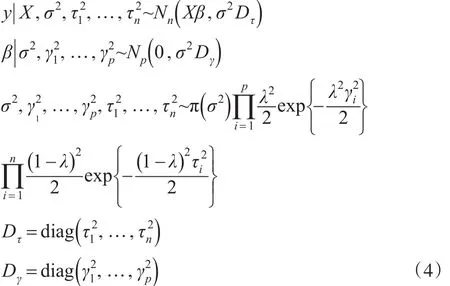
1.2 Gibbs抽樣

考慮到在所有參數的先驗分布已知的情況下，各參數的全條件分布容易抽樣，于是可通過Gibbs抽樣來推導出各參數的全條件后驗分布。通過邊緣優化，去除含有潛變量τ和γ相關的表達式，得到如下的初始邊緣貝葉斯模型：

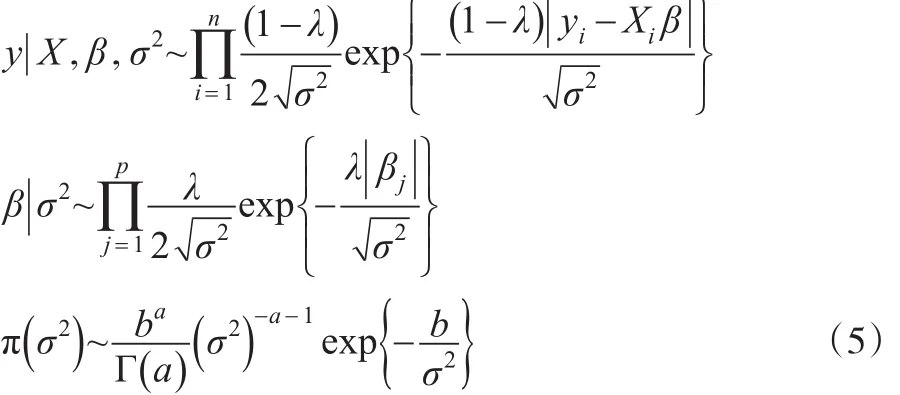
最后推導出β的全條件后驗分布服從均值為y,方差為σ2A-1的多元正態分布，其中A=XT。潛變量和的倒數的全條件后驗分布服從逆高斯分布，如下是的逆高斯參數：

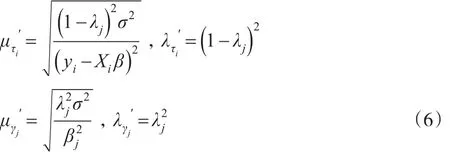
利用共軛性推導出σ2的全條件后驗分布服從參數分別為的逆伽

馬分布。

2 懲罰參數選擇

在頻率學派框架下，懲罰參數的選擇一般采用交叉驗證法進行選擇，然而在貝葉斯理論框架下，可以采用全新的辦法，比如利用無信息先驗分布的假設，從分布中模擬出參數的合理估計值。本文采用兩種不同的懲罰函數參數的選擇方法。一種方式通過邊緣極大似然方法，在基于Gibbs連續抽樣的MCEM算法[5]上不斷地更新懲罰參數λ，另一種則是通過給定懲罰參數λ合適的先驗信息，并且利用MWG（Metropolis within G）算法[6]從其后驗分布中不斷抽樣，從而達到更新懲罰參數λ的目的。

2.1 經驗貝葉斯估計

將參數β，τ，γ和λ視為缺失數據，通過邊緣極大似然來估計懲罰參數λ，然后通過EM迭代算法來更新懲罰參數，由于邊緣極大似然方法涉及到積分運算，當模型維數很高時，很難直接通過積分運算出λ的解析形式。為了解決此問題，采用MCEM算法來估計λ的值。該算法的E-步均采用吉布Gibbs采樣，根據M-步可以導出λ(k)的估計值是如下三次多項式的解：

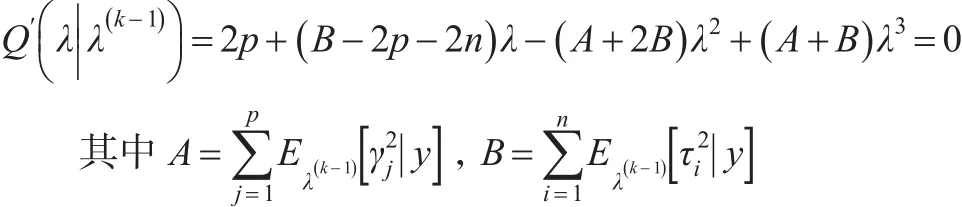
2.2 分層貝葉斯估計

為了得到所有參數的全貝葉斯模型，本文假設λ的先驗分布為π(λ)=1，此方法能夠在缺少懲罰參數信息時保證λ∈(0 ,1)，并且使得方差部分的后驗估計為通常的極大似然估計。使用上述先驗時，很難計算出λ的全條件后驗分布，但是通過計算推導出λ的全條件后驗分布與如下形式的表達式成比例：

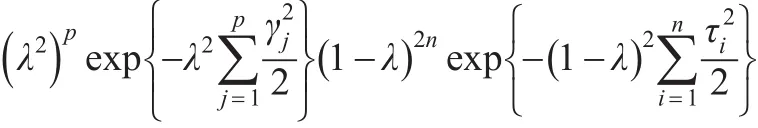
3 數據仿真

通過在不同的仿真情況下比較BBALASSO、LASSO、BLASSO的預測精度和變量選擇。LASSO選用Efron提出的5層交叉檢驗的LARS算法[2]，BLASSO選用Gramacy的BLASSO算法來選擇壓縮系數[6]。利用R軟件來實現BBLASSO的Gibbs采樣。

選用如下線性模型：

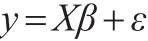
在不同的預測值和誤差項分布情形下進行仿真。每一個仿真數據集被分為一個驗證集、一個訓練集和一個測試集。從驗證集中選擇LASSO的懲罰參數λj。在選擇完懲罰參數之后，混合驗證集和訓練集來估計LASSO的β。

仿真一：本例中選定系數β=(3,1.5,2,0,0,0,0,0)′，訓練集中含有20組觀測值，驗證集中含有20組觀測值，測試集中含有200組觀測值。設計矩陣X生成自均值為0，方差為1的多元正態分布，對于所有的i和j，向量xij和xjk的相關系數為0.5|j-k|。這里誤差項ε生成自均值為0，方差分別為1，3，5的多元正態分布[7]。

仿 真 二 ：本 例 中 選 定 系 數β=(5 .6,5.6,5.6,0)′，j＜k＜4時，cov (xij,xik)=-0.39，j＜4時，cov(xij,xi4)=0.23。其他參數設置與仿真一一致，包括數據集設置[8,9]。

仿真三：本例中選定系數：

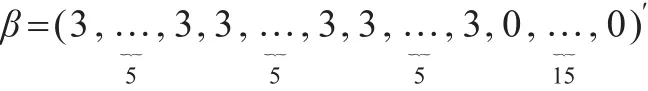
三組相互獨立的預測因子P1，P2和P3生成自均值為0，方差為1的多元正態分布。令Xi=P1+εi，i=1,…,5；這里誤差項ε生成自均值為0，方差分別為1，3，5，10，15的多元正態分布，訓練集中含有100組觀測值，驗證集中含有100組觀測值，測試集中含有400組觀測值。

為了模擬出異常值，本文通過將生成的回歸矩陣X中的任意一個元素值修改成較大的值，從而可將模型視作存在異常值模型。將仿真一、仿真二及仿真三在不同異常值個數的詳細模擬結果分別列于表1、表2及表3中，模擬過程中均選定λ=0.5，迭代10000次，每組比較都將給出不同的預測精度和變量選擇效果。

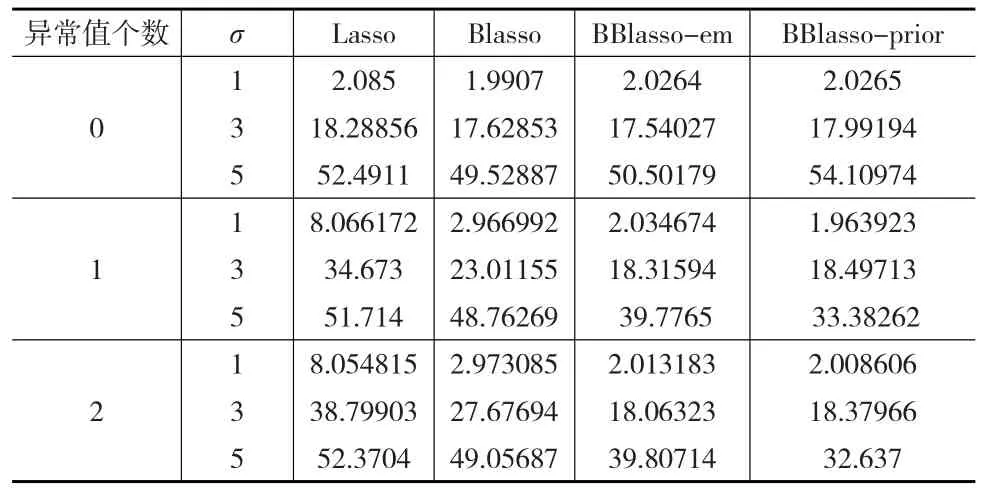
表1 仿真一中四種方法重復50次的預測精度平均值

3.1 預測精度

對四種方法重復50次仿真模擬來比較各個方法的預測精度和變量選擇。利用各仿真模擬的預測均方誤差（PSEs）平均值來判別各個方法的預測精度。

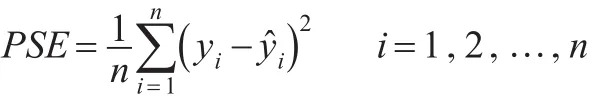
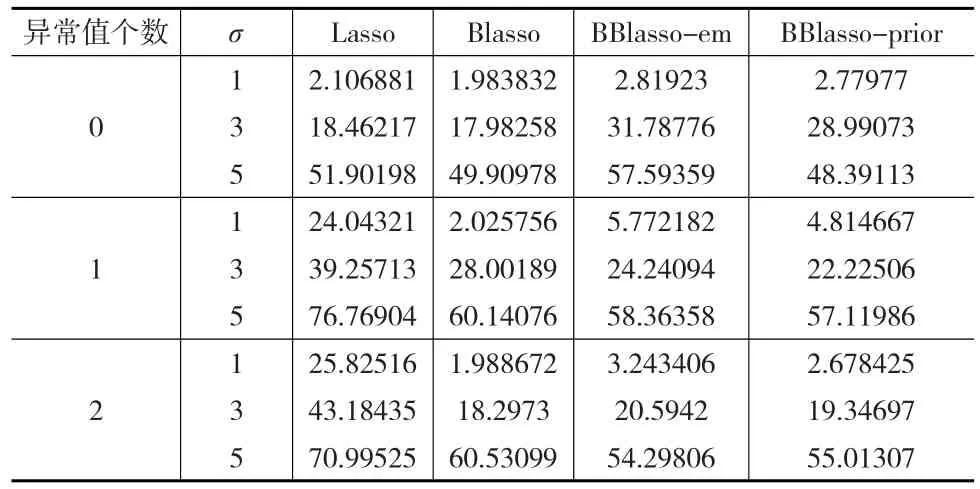
表2 仿真二中四種方法重復50次的預測精度平均值

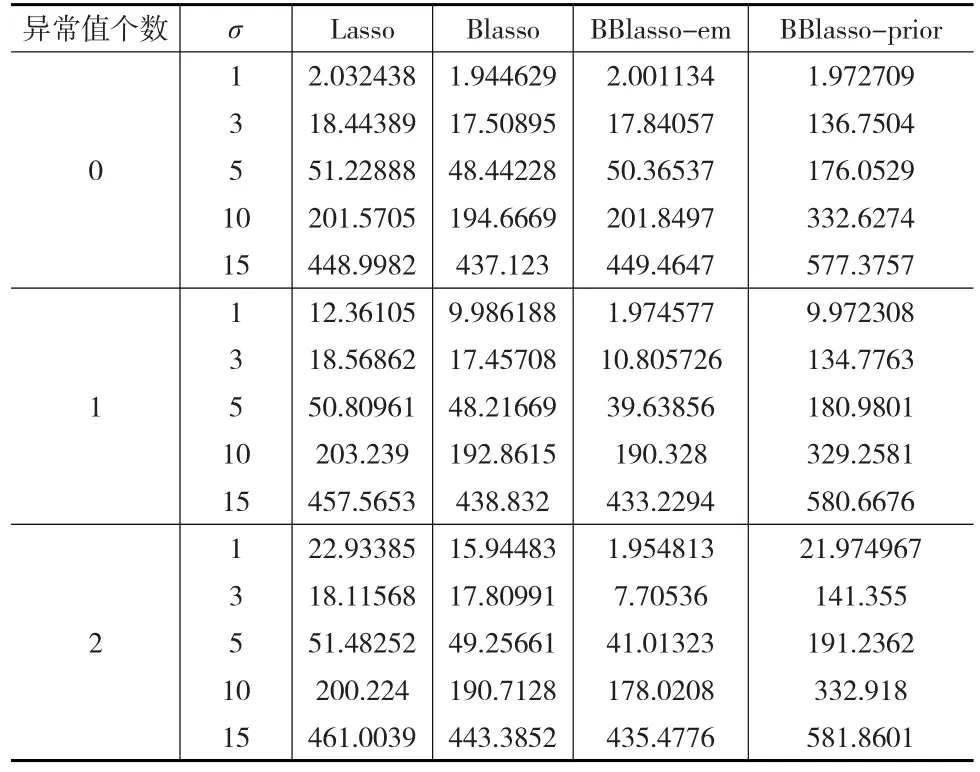
表3 仿真三中四種方法重復50次的預測精度平均值

從表1中可以看出在模型中不論是否存在異常值，Lasso預測精度相對其他三種方法較差。當模型中存在異常值時，BBlasso預測精度明顯高于Blasso預測精度，并且可以明顯看出在存在異常值模型中，BBlasso的PSEs值幾乎一致以及隨著方差以及異常值個數的增加，均方誤差也隨著增加，從而可以印證BBlasso在存在異常值乃至極端異常值的模型中是比較穩健的。

從表2中可以看出仿真二的結果與仿真一幾乎一致，結合仿真1與仿真2的模型可以看出BBlasso的兩種方法在小樣本乃至中等樣本中的表現相對其他方法有明顯優勢。然而在大樣本模型中，就不會存在著明顯的優勢，甚至會相對其他方法較差。

從表3中可以看出，當模型中不存在異常值時，BBlasso-em的預測精度與Lasso以及Blasso相差不大，然而當存在異常值時，BBlasso-em相比其他三種方法的預測精度有明顯的優勢，BBlasso-prior相對其他三種方法，在預測精度上表現較差。

3.2 變量選擇

在多元線性回歸問題中，模型變量選擇是其重要環節，本文為了比較模型變量選擇的好壞，采用ROC（Receiver Operating Characteristic）分析對四種方法的變量選擇進行評判，并通過R軟件計算AUC值（Area Under Roc Curve）直觀地體現各個方法變量選擇的效果。AUC值就是處于ROC曲線下方的那部分面積的大小。通常，AUC的值介于0.5到1之間，較大的AUC代表了在變量選擇上表現得更好。

這里僅計算了仿真一以及仿真三各方法的AUC值，之所以不計算仿真二的AUC值在于仿真二僅有四個預測因子其中還包括了一個零，計算出來的AUC值不具代表性。對于仿真一以及仿真三的AUC值見表4和表5。

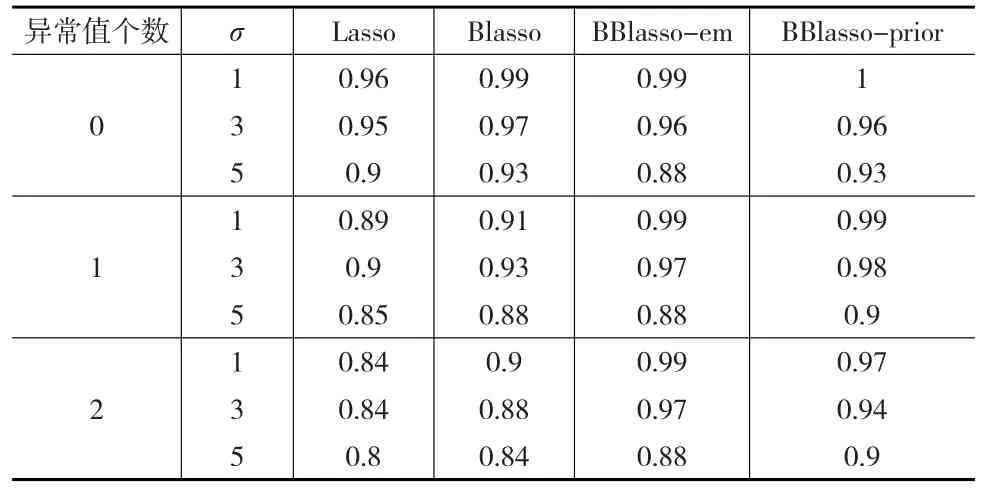
表4 仿真一中四種方法的AUC值

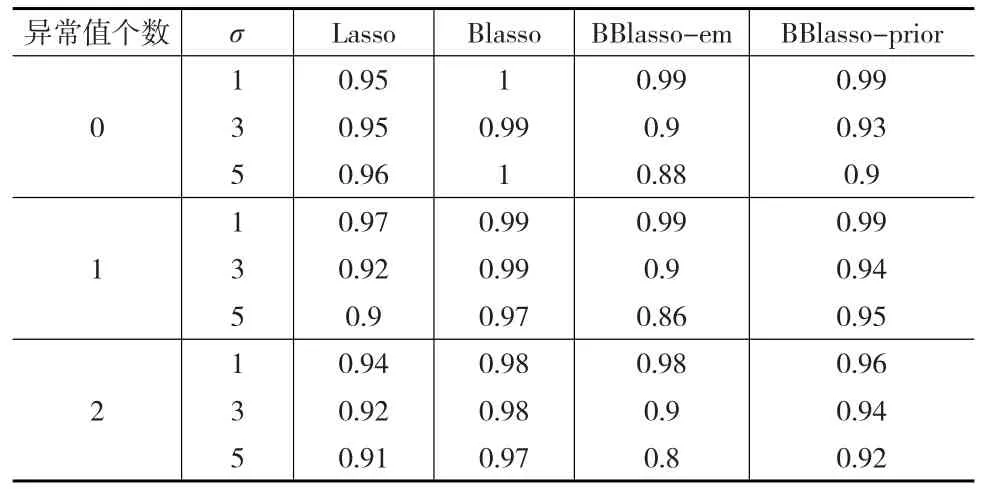
表5 仿真三中四種方法的AUC值

從表4可以看出，在仿真一中，BBlasso-em在模型不存在異常值的情況下，其AUC值與Blasso以及Lasso的AUC值幾乎一致，然而當模型存在異常值時,BBlasso-em的AUC值相比Blasso以及Lasso的AUC值有一定的優勢。

從表5可以看出，在仿真三中，Blasso的AUC值均比其他方法的AUC值大，然而不得不考慮Blasso方法在未能很好地處理異常值的情況下，所得的AUC值與BBlasso-prior的AUC值相差不大。因此也可以說明BBlasso在很好地處理異常值的情況下，變量選擇效果與其他方法相接近。

4 實例分析

4.1 前列腺數據

數據來源于Stamey 等[10]的研究，并在文獻[7,9，11]中多次被作為歷史數據使用。數據包含97例前列腺癌病例，感興趣結果變量為PSA水平，8個預測變量分別為：前列腺癌體積、前列腺重量系數、年齡、良性前列腺增生量、精囊入侵、包膜穿透、前列腺評分、前列腺評分4/5所占百分比。本文將67組前列腺數據作為訓練集，30組前列腺數據作為測試集。為了判斷誤差項是否服從正態分布，本文通過K-S檢驗，得出K-S檢驗P值為0.7012，其遠遠大于0.05，可以認為誤差項服從正態分布。此外，還通過繪制誤差項Q-Q圖，見圖1，可以看出誤差項與正態分布并沒有很大的偏差。

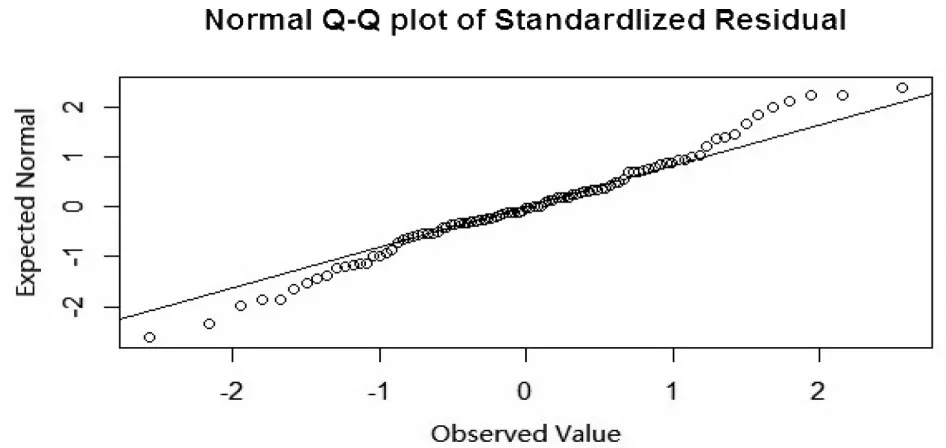
圖1 前列腺數據的誤差項Q-Q圖

通過前列腺數據，研究當誤差項服從正態分布的情況下，Lasso、Blasso、Blasso-em、blasso-prior四種方法的預測精度，利用R軟件，最終得出四種方法的預測均方誤差值(PSE)，見表6。

表6 前列腺數據在四種方法下的PSE值

從表6中可以看出，當數據誤差項服從正態分布時，四種方法的預測精度相差不大。

4.2 上證指數與宏觀經濟指標數據

隨著股市不斷發展，股市與宏觀經濟之間的密切關系完全展現出來，為了研究股市與宏觀經濟之間的關系[12]，本文選取2007年9月1日到2016年9月15日時間段上證指數共3300組數據，每日收盤價Pt作為基礎數據，將股指收益作為感興趣結果變量。一般地,收益率(也稱為對數收益率)序列定義為：

1,2,…,其中,P0,Pt分別為初始時刻及t時刻的資產價格。以8個宏觀經濟指標作為預測變量，宏觀經濟指標選用工業增加值、貨幣供應量、年利率、人民幣儲蓄存款、國內生產總值、股票成交金額、固定資產投資、進出口差額[13]。本文將2300組數據作為訓練集，1300組數據作為測試集。為了判斷誤差項是否服從正態分布，通過K-S檢驗，得出K-S檢驗P值遠遠小于0.05，可以認為誤差項不服從正態分布，并通過繪制誤差項Q-Q圖，見圖2，可以看出誤差項Q-Q圖呈現出重尾現象。

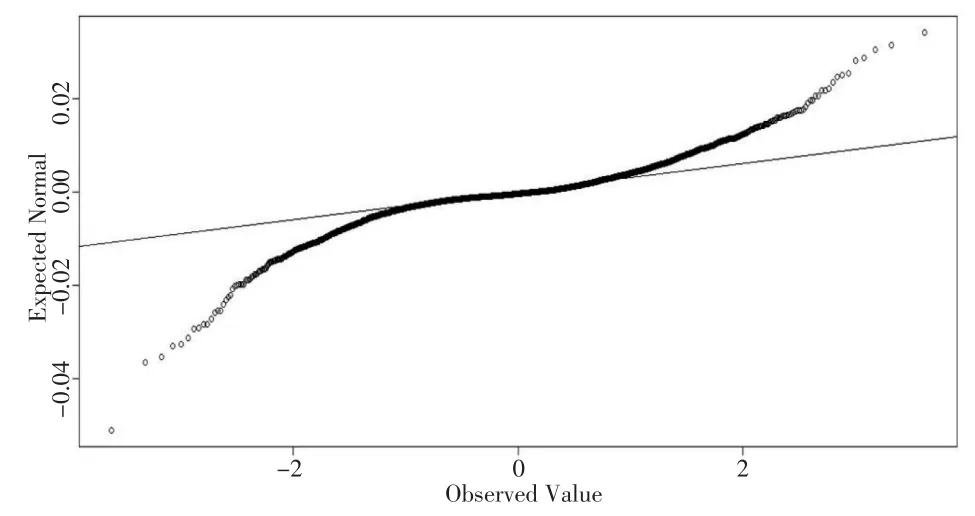
圖2 上證指數與宏觀經濟指標數據的誤差項Q-Q圖

通過上述數據，研究當誤差項服從重尾分布的情況下，Lasso、Blasso、Blasso-em、Blasso-prior四種方法的預測精度，利用R軟件，最終得出四種方法的預測均方誤差值（PSE），見下頁表7。

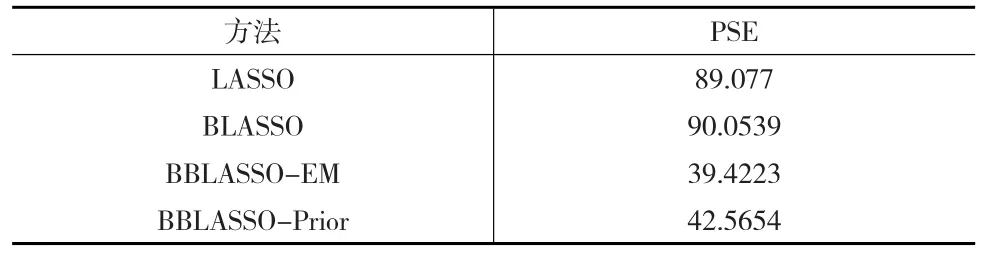
表7 上證指數與宏觀經濟指標數據在四種方法下的PSE值

從表7中可以看出，在數據誤差項服從重尾分布的情況下，LASSO與BLASSO預測精度相差不大，然而相比本文提出的BBLASSO兩種方法，還有較大差距。

5 總結

本文在Bayesian Lasso的基礎上，引入兩組潛變量，從而能夠允許模型存在誤差，通過選用未知參數以及潛變量合適的先驗分布，提出分層模型，并通過Gibbs抽樣與邊際似然，獲得未知參數的后驗分布，以及采用不同的懲罰參數結構，來不斷地更新懲罰參數。從模擬研究和實例分析可以看出，本文提出的方法相比現有的方法，在模型中存在異常值以及重尾數據的情形下更加精確，并且也可以勝任變量選擇。

當然本文也存在一些問題，即假設回歸系數先驗分布所依賴的條件參數對所有解釋變量都是相同的，也即對所有分量選用一樣的壓縮系數，為此可以進一步研究對不同分量采用不同壓縮系數，從而研究出更加有效的估計方法。

參考文獻：

[1]Tibshirani R.Regression Shrinkage and Selection Via the Lasso[J].Journal of the Royal Statistical Society,1996,58(1).

[2]Efron B,Hastie T,Johnstone I,et al.Least angle Regression[J].Ann Statist,2004,32(2).

[3]Park T,Casella G.The Bayesian Lasso[J].J Amer Statist Assoc,2008,103(482).

[4]Gramacy R B,Pantaleio E.Shrinkage Regression for Multivariate Inference With Missing Data,and an Application to Portfolio Balancing[J].Bayesian Anal,2010，5(2).

[5]袁晶.貝葉斯方法在變量選擇問題中的應用[D].濟南：山東大學博士學位論文,2013.

[6]魏艷華,王丙參,孫永輝.分組數據場合Burr-XII分布參數貝葉斯估計的混合Gibbs算法[J].統計與決策,2015,(8).

[7]Li Q,Lin N.The Bayesian Elastic Net[J].Bayesian Anal,2010,5(1).

[8]Zou H.The Adaptive Lasso and Its Oracle Properties[J].J Amer Statist Assoc,2006,101(476).

[9]Leng C,Tran M N,Nott D.Bayesian Adaptive Lasso[J].Ann Inst Statist Math,2014,66(2).

[10]Stamey T A,Kabalin J N,McNeal J E,et al.Prostate Specific Antigen in the Diagnosis and Treatment of Adenocarcinoma of the Prostate.ii.Radical Prostatectomy Treated Patients[J].Journal of Urology，1989,141(5).

[11]Zou H,Hastie T.Regularization and Variable Selection via the Elastic net[J].J R Stat Soc Ser B Statist Methodol,2005,67(2).

[12]尚鵬岳,李勝宏.上證指數與宏觀經濟指標協整關系的實證分析[J].預測,2002,(4).

[13]王曉燕,呂效國,范玉,張媛.上證指數與宏觀經濟指標關系的實證分析[J].商業時代,2012,(10).