結冰風洞中液滴相變效應數值模擬
郭向東,王梓旭,李明,劉蓓
1.中國空氣動力研究與發展中心 空氣動力學國家重點實驗室,綿陽 621000 2. 中國空氣動力研究與發展中心 飛行器結冰與防除冰重點實驗室,綿陽 621000
飛機結冰廣泛存在于飛行實踐中,并嚴重威脅飛行安全[1-2]。研究飛機結冰的主要途徑包括數值模擬、結冰風洞試驗和飛行試驗3種,其中結冰風洞試驗顧名思義是利用結冰風洞在地面模擬飛機結冰過程,驗證飛機防除冰系統,開展飛機結冰問題研究[3]。相對于數值模擬和飛行試驗,結冰風洞試驗具有結冰條件易控、試驗成本相對較低、結果可靠等優點,是目前研究飛機結冰的主要手段。為模擬高空低溫低壓的云霧環境,結冰風洞主要包括制冷系統、高度模擬系統和噴霧系統三大部分,其中噴霧系統利用噴嘴在風洞穩定段內生成大量懸浮液滴,隨后液滴由低溫氣流攜帶進入試驗段,形成試驗所需的過冷水滴云霧[4]。結冰試驗中,氣流靜溫低于冰點,為防止噴霧系統中液態水結冰,須采用加熱方式提高液態水溫度,這樣便導致穩定段內生成的液滴溫度高于氣流靜溫,通常情況下,液滴會與氣流發生充分的熱交換,進而在試驗段內達到過冷狀態(液滴溫度與試驗段靜溫一致),形成試驗所需的過冷水滴[5]。但是,由于水滴與氣流間的熱交換過程十分復雜,涉及對流傳熱、相變傳質和三維收縮效應等多物理過程的耦合作用,試驗參數的變化可能導致試驗段內液滴偏離過冷狀態,進而改變積冰生長過程和冰形特征,影響結冰風洞試驗結果,因此探索結冰風洞中液滴傳熱過程,揭示試驗參數的影響規律,評估液滴過冷狀態,對結冰風洞試驗準確模擬結冰過程具有重要意義。
針對結冰風洞液滴過冷問題,Willbanks和Schulzt[6]率先發展了基于拉格朗日法的運動液滴傳質傳熱計算方法,并對發動機高空試驗臺內的液滴傳熱過程開展了研究,隨后Miller等[7]采用這一方法,研究了NASA Glenn IRT結冰風洞內的液滴過冷問題,發現初始液滴溫度對液滴過冷狀態無顯著影響,此外Bellucci等[8]采用試驗方法對CIRA結冰風洞高速試驗段和低速試驗段構型的液滴過冷狀態進行了評估。但是這些研究主要關注工程層面上液滴過冷狀態的評估,缺乏對結冰風洞中液滴傳熱傳質過程的規律性認識。
近年來,隨著國內大型結冰風洞——3 m×2 m結冰風洞的建成,液滴過冷問題逐漸引起了一些國內學者的關注[9-10]。其中郭向東等[10]發展了基于Euler法的氣液兩相耦合流動計算方法,研究了3 m×2 m結冰風洞主試驗段構型液滴傳熱過程,并評估了液滴過冷狀態,研究結果表明結冰風洞中液滴傳熱過程可以分為準一維傳熱和三維收縮傳熱兩個階段,其中三維收縮效應對液滴過冷狀態起決定性作用,但是他們的研究中未考慮液滴相變傳質對液滴傳熱過程的影響,導致對結冰風洞液滴過冷狀態的評估結果較為保守。
因此,本文在郭向東等的計算方法基礎上,進一步引入Hill矩方法[11],發展了基于Euler法的氣液兩相傳質傳熱耦合流動計算方法,實現了液滴相變傳質過程的模擬。進而利用該方法,針對3 m×2 m結冰風洞主試驗段構型,考察了液滴相變效應對液滴傳熱過程的影響,揭示了相變效應的影響規律,開展了參數影響研究,分析了相對濕度、試驗段氣流速度和液滴尺寸對液滴傳質傳熱過程的影響,評估了液滴過冷狀態,為國內飛機結冰地面模擬試驗數據應用評估提供支撐。
1 計算方法
1.1 控制方程和物理模型
本文借鑒了文獻[10]中基于Euler法的氣液兩相耦合流動計算方法,進一步耦合Hill矩函數方程組[12-14],實現了相變傳質過程的模擬。為獲得簡化物理模型,對氣液兩相進行以下假設[15]:①氣相為理想氣體,遵循理想氣體法則;②液滴為球形,不發生變形和破碎,液滴間不發生碰撞;③液滴內溫度均勻分布;④忽略重力效應;⑤ 黏性和熱傳導效應僅發生在氣液兩相間;⑥不考慮液滴凍結過程以及水蒸氣凝結成核過程。
基于以上假設,簡化后的控制方程組為
1) 氣相方程組
(1)
(2)
(3)
(4)
2) 液相方程組
(5)
(6)
(7)
3) 矩函數方程組
(8)
(9)
(10)
式中:下標g和d分別代表氣相和液相;ρ、p、V和E分別為密度、壓力、速度和單位質量總能量;氣相能量Eg和液相能量Ed的表達式分別為
(11)
式中:cv為氣相定容比熱;cl為液滴比熱;T為溫度。
σ和α分別為液滴有效密度和水蒸氣質量分數,其中σ對應液態水含量(LWC);n階矩函數定義為
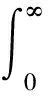
(12)
其中:r為液滴半徑;f為粒子尺寸分布函數;Q0、Q1和Q2為零階、一階和二階矩函數,根據定義可見Q0表示單位體積內液滴總個數。
S0為質量源項,表示為
(13)
式中:ρl為液滴物理密度;dr/dt為液滴半徑變化率。
SD和SM分別為兩相動量交換源項和兩相間傳質引起的動量傳遞源項,表示為
SD=Q0FD,SM=S0Vd
(14)
式中:FD為單個液滴受到的氣相作用力。
SEg和SEd分別為氣相和液相能量源項,表示為
(15)
式中:qheat與qrad分別為單個液滴與氣相間的對流傳熱率和輻射傳熱率;qgas,mass和qliquid,mass分別為單位質量傳質引起的氣相和液相能量變化率,表示為[16-17]
(16)
其中:cp為水蒸氣定壓比熱;L為汽化潛熱。
S1和S2分別為一階和二階矩函數方程源項,表示為
(17)
單個液滴受到的氣相作用力FD和單個液滴與氣相間的對流傳熱率qheat表示為[18]
(18)
qheat=Nukgπd(Tg-Td)
(19)
式中:d為液滴直徑;μg為氣相黏性系數;kg為氣相熱傳導系數;Red為液滴相對雷諾數,表示為
(20)
CD為液滴阻力系數,針對球型液滴,采用Schiller-Naumann圓球阻力模型,表示為
(21)
針對球型液滴,Nu采用Ranz-Marshall半經驗關系式,表示為
(22)
式中:Pr為Prandtl數。
單個液滴與氣流間的輻射傳熱率qrad表示為[19]
(23)
式中:ε為熱輻射發射率,根據文獻[19],ε取0.95;σSB為Stefan-Boltzmann常數。
(24)
式中:DAB為二元質量擴散系數;Rv為水蒸氣氣體常數;pv,s為液滴表面飽和水氣壓;Hu為相對濕度,表示為
(25)
式中:pv,∞為氣相環境中水蒸氣分壓。
Sh為Sherwood數,針對球型液滴,Sh采用Ranz-Marshall半經驗關系式,表示為
(26)
式中:Sc為Schmidt數。根據文獻[16,21],Ranz-Marshall半經驗關系式適用于Red<137、溫度低于0 ℃時球型液滴的傳質傳熱過程,匹配本文的研究范圍(尤其對于高風速工況下依然成立),因此本文計算模型中Nu和Sh采用該關系式。
1.2 數值方法
本文采用與文獻[10]相同的數值方法,控制方程組采用有限體積方法離散,非定常項采用二階Euler格式離散,空間輸運項采用二階迎風型的Roe格式離散,源項采用隱式格式[10]。
氣液兩相邊界條件采用不同形式處理:氣相入口條件采用壓力入口,出口條件采用壓力出口,壁面采用無黏滑移壁面條件(1.1節假設⑤);液相入口條件采用速度入口,出口采用出流條件,壁面處認為液滴可以直接穿過,不考慮壁面對液相的作用。
1.3 驗證算例
選取文獻[21]中的試驗結果驗證本文計算方法。文獻[21]采用懸掛液滴試驗方法研究了液滴凍結過程中的液滴溫度變化特性,文中將液滴凍結過程分為過冷(Supercooling Stage)、復輝(Recalescence Stage)、凍結(Freezing Stage)和冷卻(Cooling Stage)4個階段,其中過冷階段對應本文研究的內容,因此選取文獻中過冷階段的試驗結果驗證本文計算方法。驗證結果如圖1所示,圖中:Va和Ta分別表示氣流速率和氣流靜溫。從圖中可以看出:本文計算結果與試驗結果吻合得較好,不同工況下液滴溫度誤差均小于1%,因此本文計算方法可以合理模擬液滴過冷階段的傳熱過程。針對以上的驗證過程,應該指出的是考慮到懸掛液滴法對液滴尺寸和試驗風速的限制,該方法僅獲得了大液滴(毫米量級)低風速(小于1 m/s)下的試驗結果,而缺乏小液滴(微米量級)高風速的試驗結果。進一步,文獻[21]指出,盡管缺乏真實噴霧的試驗數據,但是試驗數據中液滴相對雷諾數范圍(36 本節針對3 m×2 m結冰風洞主試驗段收縮構型,采用本文發展的計算方法,考察了基準工況下液滴相變效應對液滴傳熱過程的影響,揭示了相變效應的影響規律,開展了參數影響研究,分析了相對濕度、試驗段氣流速度和液滴尺寸對液滴傳質傳熱過程的影響,評估了試驗段中心處液滴過冷狀態。 3 m×2 m結冰風洞主試驗段構型如圖2所示,該構型包括穩定段、收縮段和試驗段3部分,其中構型入口截面為高8 m×寬11 m,位于穩定段噴霧耙處,出口截面為高2 m×寬3 m,位于試驗段中心處,構型全長16 m,收縮比為14.67。 根據文獻[10]的研究結果可知,試驗段氣流速度和液滴尺寸是影響液滴過冷狀態的主要參數,因此本文選取相對濕度、試驗段氣流速度和液滴尺寸3個參數開展參數研究,計算工況矩陣如表1所示,表中LWCi、di、Tdi、T0i、Udi、UTS和Hui分別代表初始液態水含量、初始液滴直徑、初始液滴溫度、初始氣流總溫、初始液滴速率、試驗段氣流速度、初始相對濕度。Case 1為基準工況,考察典型工況下結冰風洞中相變對液滴傳熱過程的影響;Case 2選取了70%、80%、90%和100%這4個典型的相對濕度狀態,考察相對濕度的影響;Case 3選取了55 、77、130、164 m/s這4個典型試驗段風速,考察氣流速度的影響,其中各風速對應的入口總壓分別為2 000、4 000、12 000、20 000 Pa,參考壓力為105Pa;Case 4選取了40、60、80、100 μm這4個典型液滴直徑,考察液滴尺寸的影響,值得指出的是由于假設液滴為球型,不考慮液滴變形和破碎等動力學特性,因此僅選取了小尺寸液滴開展研究。 表1 計算工況矩陣Table 1 Calculation condition matrix 基準工況選取FAR Part25 附錄C中典型結冰條件[22],為考察相變對液滴傳熱過程的影響,下文通過對比構型內液滴和顆粒的傳熱過程,進而揭示液滴相變效應的影響規律,其中針對顆粒傳熱過程的模擬,本文采用文獻[10]中的計算方法來實現。 圖3給出了基準工況下構型中心線處氣流靜溫和液滴溫度變化曲線,從圖中可以看出,類似于文獻[10]中顆粒傳熱過程,整個液滴傳熱過程近似以構型6 m處截面為界分成準一維傳熱和三維收縮傳熱兩個階段。在準一維傳熱階段內(入口至6 m處截面,包括穩定段和收縮段入口區域),風洞型面變化較緩,氣流以準一維方式低速流動,氣流速度和靜溫變化較小,接近入口流速和總溫,液滴以準一維穩態方式傳熱;在三維收縮傳熱階段內(6 m處截面至出口,包括收縮段后部區域和試驗段),風洞型面變化較大,三維收縮效應較強,氣流場在此階段內發生了顯著變化,氣流速度加速增大,氣流靜溫則等熵下降,出口氣流速度越大,出口氣流靜溫越低,三維收縮效應(氣流可壓縮性)顯著影響液滴傳熱過程,液滴以三維動態方式傳熱。對比液滴與顆粒的溫度變化曲線可見:在準一維傳熱階段,液滴溫度下降趨勢快于顆粒溫度,當液滴溫度和顆粒溫度趨于穩定時(約在0.6 m處),液滴溫度(約-5.4 ℃)低于顆粒溫度(-5 ℃),此時液滴溫度稱為液滴濕球溫度[16];在三維收縮傳熱階段,液滴溫度下降趨勢慢于顆粒,最終在構型出口處(試驗段中心),液滴溫度(-7.41 ℃)高于顆粒溫度(-7.77 ℃)。 圖4給出了構型中心線處液滴直徑和相對濕度變化曲線,從圖中可以看出:結冰風洞中液滴經歷了先蒸發后凝結兩個階段,在準一維傳熱階段,氣流中水蒸氣未達到飽和狀態,液滴處于蒸發狀態,液滴直徑不斷減小,同時蒸發產生的水蒸氣則使氣流的相對濕度不斷增大;在三維收縮階段,氣流靜溫迅速下降,氣流飽和水汽壓降低,而水蒸氣分壓變化較小(適用于低速流動),導致氣流的相對濕度迅速增大(對應式(25)),氣流中水蒸氣從未飽和狀態轉換為過飽和狀態,液滴則從蒸發狀態轉換為凝結狀態。 進一步理論分析相變效應對液滴傳熱的影響。首先液相能量方程式(7)可以化簡為 (27) 式中:由于液滴過冷階段輻射傳熱遠小于對流傳熱和相變傳熱,因此忽略輻射傳熱項,同時聯立式(19)和式(24),則式(27)可化簡為 (28) ξheat+ξmass (29) 式中:ξheat為對流傳熱引起的液滴溫度空間變化率;ξmass為液滴相變引起的液滴溫度空間變化率。需要指出的是,式(29)是在一維定常流動條件下得到的,但是對于三維收縮階段,構型中心線處的氣流沿流向加速流動,仍可以近似認為氣流運動為準一維,因此式(29)適用于構型中心線處整個液滴傳熱過程的分析。 圖5給出了構型中心線處ξmass和ξheat的變化曲線,從圖中可以看出,在準一維傳熱階段,當溫度較高的液滴進入未飽和的低溫氣流(Hui<100%)中時,液滴與氣流間發生對流傳熱,液滴向氣流傳遞熱能(ξheat<0),同時蒸發效應從液滴吸收所需的汽化潛熱(ξmass<0),而顆粒與氣流間僅發生對流傳熱過程,因此液滴溫度下降速度快于顆粒的速度(0~0.6 m);當液滴溫度下降至氣流靜溫時[23],由于蒸發效應仍持續從液滴吸收熱量,因此液滴溫度會持續下降,但對于顆粒而言,其溫度此時將會與氣流靜溫保持一致,顆粒與氣流間的對流傳熱過程停止,顆粒達到穩定狀態;進一步,當液滴溫度下降至液滴濕球溫度時,蒸發效應所需的汽化潛熱(ξmass<0)與氣流向液滴傳遞的熱能(ξheat>0)達到平衡(|ξmass|=|ξheat|),液滴溫度趨于穩定,此時ξmass與ξheat沿流向(x軸)對稱分布(0.6~6 m),液滴進入穩定蒸發階段。在三維收縮階段,三維收縮效應導致氣流靜溫迅速下降,液滴穩定蒸發過程被破壞,ξmass與ξheat不再對稱分布,液滴溫度下降(ξmass+ξheat<0);此階段內對流傳熱的能量傳遞方向發生了轉換,即ξheat>0轉換為ξheat<0,促進了液滴溫度下降,同時氣流中水蒸氣從未飽和狀態轉換為過飽和狀態,液滴則從蒸發狀態轉換為凝結狀態,即ξmass<0轉換為ξmass>0,則抑制了液滴溫度下降,而顆粒與氣流間僅存在對流換熱過程,缺少了凝結過程的抑制效應,因此可見凝結效應是三維收縮階段內液滴溫度下降趨勢慢于顆粒的主要原因,最終導致構型出口處(試驗段中心),液滴溫度高于顆粒溫度。 首先考察相對濕度的影響,在結冰風洞試驗中,為避免氣流濕度過低導致液滴大量蒸發,會采用加濕器提高風洞回路內氣流濕度,因此此處選取較高的相對濕度參數開展研究。 圖6(a)和圖6(b)給出了不同初始相對濕度下構型中心線處液滴直徑和相對濕度變化曲線,從圖中可以看出:在準一維傳熱階段,隨著初始相對濕度的增加,液滴尺寸的減小趨勢減慢,表明液滴蒸發效應減弱,尤其當濕度100%時,液滴尺寸在溫度穩定階段不再發生變化,蒸發效應消失;與此相反,在三維收縮階段,隨著初始相對濕度的增加,水蒸氣過飽和程度增強,液滴尺寸的增大趨勢加快,表明凝結效應增強。 圖6(c)給出了不同初始相對濕度下構型中心線處液滴溫度變化曲線,從圖中可以看出:在準一維傳熱階段,隨著初始相對濕度增加,液滴蒸發效應減弱,液滴溫度下降趨勢減慢(如放大圖所示),當液滴趨于穩定蒸發狀態時(約在0.6 m處),初始相對濕度越大則液滴濕球溫度越高,尤其當相對濕度為100%時,蒸發效應消失,液滴溫度與顆粒溫度趨于一致;在三維收縮傳熱階段,隨著初始相對濕度增加,液滴凝結效應增強,導致構型出口處(試驗段中心)液滴溫度不斷增大,尤其當相對濕度100%時,液滴凝結效應最強,出口液滴溫度最高,比顆粒溫度高近1 ℃。 圖7給出了不同初始相對濕度下構型出口中心處液氣溫度差,從圖中可以看出:隨著初始相對濕度增加,液氣溫差不斷增大,其中初始相對濕度為70%時,液滴溫差與顆粒的一致,約為0.1 ℃,而當初始相對濕度增加至100%時,液滴溫差增至約0.87 ℃,比顆粒溫度差高近0.8 ℃。由此可見,相對濕度會影響試驗段內液滴過冷狀態,但影響程度較弱,本文計算工況下最大液氣溫差(相對濕度為100%)小于1 ℃,液滴仍認為處于過冷狀態。 考察試驗段氣流速度的影響,根據3 m×2 m結冰風洞典型試驗工況,選取55、77、130、164 m/s這4個試驗段氣流速度開展研究,其中各試驗段氣流速度(構型出口氣流速度)對應的穩定段氣流速度(構型入口氣流速度)分別為4.11、5.70、9.15及11.00 m/s。 圖8給出了不同試驗段氣流速度下構型中心線處液滴直徑和相對濕度變化曲線,從圖中可以看出:在準一維傳熱階段,隨著試驗段氣流速度的增加,穩定段氣流速度增大,液滴相變時間減少,液滴尺寸的減小趨勢減慢,表明蒸發效應減弱;在三維收縮階段,隨著試驗段氣流速度的增加,盡管液滴相變時間不斷減少,但是在三維收縮效應的影響下,氣流靜溫顯著降低,水蒸氣過飽和度顯著增大,導致液滴尺寸的增大趨勢加快,進而表明凝結效應增強。 圖9給出了不同試驗段氣流速度下構型中心線處氣流靜溫和液滴溫度變化曲線,從圖中可以看出,在準一維傳熱階段,隨著試驗段氣流速度的增加,穩定段氣流速度增大,但是由于穩定段速度增大幅度較小(從約4 m/s增至11 m/s),氣流可壓縮性較弱,因此各工況下的氣流靜溫和液滴溫度變化趨勢無顯著差異,氣流靜溫接近氣流總溫,并且液滴溫度穩定后,液滴濕球溫度也基本一致。在三維收縮階段,隨著試驗段氣流速度的增加,氣流可壓縮性顯著增強,試驗段氣流靜溫顯著下降,具體的當試驗段氣流速度從55 m/s增至164 m/s時,試驗段氣流靜溫約從-7 ℃降至-18 ℃,因此在結冰風洞試驗中,氣流可壓縮性導致的氣流靜溫變化是不可忽略的;同時,在這一階段隨著試驗段氣流速度的增加,液滴溫度的下降趨勢加快,但是相對于顆粒,由于凝結效應的不斷增強,抑制了液滴溫度的下降趨勢,導致出口處(試驗段中心)液滴與顆粒溫差不斷增大。 圖10給出了不同試驗段氣流速度下構型出口中心處液氣溫度差,從圖中可以看出:隨著試驗段氣流速度的增加,液氣溫差不斷增大,并且在相變效應的影響下,其增大趨勢強于顆粒,其中試驗段氣流速度為55 m/s時,液滴溫差約為0.3 ℃,而顆粒的溫差則趨近于0 ℃,當試驗段氣流速度增加至164 m/s時,液滴溫差增至約3.3 ℃,比顆粒的溫差高近2 ℃。由此可見,氣流速度會顯著影響試驗段內液滴過冷狀態,同時相變效應則會顯著增強影響程度,其中小尺寸液滴(40 μm≤di≤100 μm)在高風速時(UTS≥164 m/s)將偏離過冷狀態(液氣溫差超過3 ℃)。 最后,考察液滴尺寸的影響,由于采用球型液滴阻力模型,不考慮液滴變形和破碎效應,因此在We數的約束下[24],僅選擇尺寸較小的液滴,以較好地滿足球型液滴假設。 圖12給出了不同初始液滴尺寸下構型中心線處液滴溫度變化曲線,從圖中可以看出:在準一維傳熱階段,隨著初始液滴尺寸增加,液滴熱容量增大,液滴溫度下降趨勢減慢,液滴溫度穩定后,液滴濕球溫度無顯著變化,液滴與顆粒溫差基本一致;在三維收縮階段,隨著初始液滴尺寸增加,液滴溫度下降趨勢減慢(與文獻[10]的結論一致),但是相對于顆粒,凝結效應不斷減弱,促進了液滴溫度的下降趨勢,導致出口處(試驗段中心)液滴與顆粒溫差不斷減小。 圖13給出了不同初始液滴尺寸下構型出口中心處液氣溫度差,從圖中可以看出:隨著初始液滴尺寸增加,液氣溫差不斷增大,但是在相變效應的影響下,其增大趨勢弱于顆粒的溫度差,其中液滴直徑為40 μm時,液滴溫度差約為0.6 ℃,而顆粒溫度差約為0.1 ℃,當液滴直徑增加至100 μm時,液滴溫度差增至約0.85 ℃,比顆粒的溫差低近0.05 ℃。由此可見,液滴尺寸會影響試驗段液滴過冷狀態,但相變效應卻會減弱影響程差,其中在低風速(UTS≤77 m/s)試驗工況下,小尺寸液滴(di≤100 μm)仍可以認為處于過冷狀態(液氣溫差小于1 ℃),這與文獻[10]的評估結果一致。 本文發展了基于Euler法的氣液兩相傳質傳熱耦合流動計算方法,模擬了結冰風洞中氣液兩相傳質傳熱耦合流動過程,研究了結冰風洞中液滴相變效應。 1) 結冰風洞中液滴經歷了先蒸發后凝結兩個階段。在準一維傳熱階段,液滴為蒸發狀態,蒸發效應加快了液滴溫度下降趨勢,并且促使液滴溫度趨于濕球溫度;在三維收縮階段,液滴則從蒸發狀態轉換為凝結狀態,凝結效應減慢了液滴溫度下降趨勢,導致構型出口處(試驗段中心)液氣溫差增大,影響液滴過冷狀態。 2) 初始相對濕度增加,會減弱蒸發效應而增強凝結效應,進而影響試驗段內液滴過冷狀態。但其影響程度較弱,本文計算工況下最大液氣溫差(相對濕度為100%)小于1 ℃,液滴仍認為處于過冷狀態。 3) 氣流速度會顯著影響試驗段內液滴過冷狀態,隨著氣流速度的增加,蒸發效應減弱而凝結效應增強,進而顯著增強了影響程度,其中小尺寸液滴(40 μm≤di≤100 μm)在高風速時(UTS≥164 m/s)將偏離過冷狀態(液氣溫差超過3 ℃)。 4) 初始液滴尺寸增加,會導致蒸發效應和凝結效應均減弱,進而減弱了液滴尺寸對試驗段內液滴過冷狀態的影響程度,對于小尺寸液滴(di≤100 μm)在低風速(UTS≤77 m/s)試驗工況下,仍可以認為處于過冷狀態(液氣溫差小于1 ℃)。 需要指出的是,實際結冰風洞中,氣液兩相流動過程十分復雜,涉及動量傳遞、質量傳遞和能量傳遞等多物理過程的強耦合作用,而本文發展的基于Euler法的氣液兩相傳質傳熱耦合流動計算方法是基于一定假設下的簡化分析方法,因此開展計算方法驗證試驗則是下一步急需開展的工作。 此外,針對液滴直徑超過100 μm的大尺寸液滴,由于其存在變形和破碎等動力學效應,超出了本文采用的球形液滴數學模型適用范圍,因此建立大尺寸液滴傳質傳熱模型,則是今后需要開展的研究。 參 考 文 獻 [1] 杜雁霞, 李明, 桂業偉, 等. 飛機結冰熱力學行為研究綜述[J]. 航空學報, 2017, 38(2): 520706. DU Y X,LI M, GUI Y W, et al. Review of thermodynamic behaviors in aircraft icing process[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(2): 520706 (in Chinese). [2] 桂業偉, 周志宏, 李穎暉, 等. 關于飛機結冰的多重安全邊界問題[J]. 航空學報, 2017, 38(2): 520723. GUI Y W, ZHOU Z H, LI Y H, et al. Multiple safety boundaries protection on aircraft icing[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(2): 520723 (in Chinese). [3] 易賢, 王斌, 李偉斌, 等. 飛機結冰冰形測量方法研究進展[J]. 航空學報, 2017, 38(2): 520700. YI X, WANG B, LI W B, et al. Research progress on ice shape measurement approaches for aircraft icing[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(2): 520700 (in Chinese). [4] RAGNI A, ESPOSITO B, MARRAZZO M, et al. Calibration of the CIRA IWT in the high speed configuration[C]//43th AIAA Aerospace Science Meeting and Exhibit. Reston, VA: AIAA, 2005. [5] STEEN L E, IDE R F, van ZANTE J F, et al. NASA Glenn icing research tunnel: 2014 and 2015 cloud calibration procedures and results: NASA/TM-2015-218758 [R]. Washington, D. C. : NASA, 2015. [6] WILLBANKS C E, SCHULZT R J. Analytical study of icing simulation for turbine engines in altitude test cells[J]. Journal of Aircraft, 1975, 12(12): 960-967. [7] MILLER D R, ADDY H E, IDE R F. A study of large droplet ice accretions in the nasa glenn irt at near-freezing conditions: NASA TM-1996-107142-REV1 [R]. Washington, D. C. : NASA, 1996. [8] BELLUCCI M, ESPOSITO B M, MARRAZZO M, et al. Calibration of the CIRA IWT in the low speed configuration[C]∥45th AIAA Aerospace Science Meeting and Exhibit. Reston, VA: AIAA,2007. [9] 易賢, 馬洪林, 王開春, 等. 結冰風洞液滴運動及傳質傳熱特性分析[J]. 四川大學學報, 2012, 44(2): 132-135. YI X, MA H L, WANG K C, et al. Analysis of water droplet movement and heat / mass transfer in an icing wind tunnel[J]. Journal of Sichuan University, 2012, 44(2): 132-135 (in Chinese). [10] 郭向東,王梓旭,李明,等.結冰風洞中液滴過冷特性數值研究[J].航空學報, 2018, 39(1): 121254. GUO X D, WANG Z X, LI M, et al. Numerical study of droplet supercooling in an icing wind tunnel [J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(1): 121254 (in Chinese). [11] HILL P G. Condensation of water vapor during supersonic expansion in nozzles[J]. Journal of Fluid Mechanics, 1966, 25(3): 593-620. [12] CHENG W, LUO X S, van DONGEN M E H. On condensation-induced waves[J]. Journal of Fluid Mechanics, 2010, 651(1): 145-164. [13] 郭向東, 黃生洪, 吳穎川, 等. 氫燃料燃燒加熱風洞中水蒸氣相變效應的數值研究[J]. 推進技術, 2017, 38(4):932-941. GUO X D, HUANG S H, WU Y C, et al. Numerical evaluation of water vapor phase transition effects in a hydrogen-fueled combustion-heated wind tunnel[J]. Journal of Propulsion Technology, 2017, 38(4): 932-941 (in Chinese). [14] CAO Y, LUO X S. Numerical study on Homogeneous condensation in a vortex[J]. Procedia Engineering, 2015, 126: 607-611. [15] LUO X S, WANG G, OLIVIER H. Parametric investigation of particle acceleration in high enthalpy conical nozzle flows for coating applications[J]. Shock Waves, 2008, 17(5): 351-362. [16] KERSEY J, LOTH E, LANKFORD D. Effects of Evaporating Droplets on Shock Waves[J]. AIAA Journal, 2010, 48(9): 1975-1986. [17] RUSSO E, KUERTEN J G M, van der Geld C W M, et al. Water droplet condensation and evaporation in turbulent channel flow[J]. Journal of Fluid Mechanics, 2014, 749: 666-700. [18] SAITO T. Numerical analysis of dusty-gas flows[J]. Journal of Computational Physics, 2002, 176(1): 129-144. [19] FUJITA A, KUROSE R, KOMORI S. Experimental study on effect of relative humidity on heat transfer of an evaporating water droplet in air flow[J]. International Journal of Heat and Mass Transfer, 2010, 36(3): 244-247. [20] MILLER R S, HARSTAD K, BELLAN J. Evaluation of equilibrium and non-equilibrium evaporation models for many-droplet gas-liquid flow simulations[J]. International Journal of Multiphase Flow, 1998, 24(6): 1025-1055. [21] HINDMARSH J P, RUSSEL A B, CHEN X D. Experimental and numerical analysis of the temperature transition of a suspended freezing water droplet[J]. International Journal of Heat and Mass Transfer, 2003, 46(7): 1199-1213. [22] COBER S, BERNSTEIN B, JECK R, et al. Data and analysis for the development of an engineering standard for supercooled large drop conditions: DOT/FAA/AR-09/10[R]. Washington, D. C.: FAA, 2009. [23] KUROSE R, FUJITA A, KOMORI S. Effect of relative humidity on heat transfer across the surface of an evaporating water droplet in air flow[J]. Journal of Fluid Mechanics, 2009, 624: 57-67. [24] LUXFORD G. Experimental and modelling investigation of the deformation, drag and break-up of drizzle droplets subjected to strong aerodynamic forces in relation to SLD aircraft icing[D]. Bedfordshire: Cranfield University, 2005: 5-7 .2 結果與分析

2.1 基準工況
2.2 相對濕度影響
2.3 試驗段氣流速度影響
2.4 液滴尺寸影響
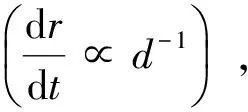
3 結 論

