高溫超導發電機勵磁系統變論域模糊控制

張蘭勇，孟　坤，朱　帥

(1.哈爾濱工程大學 自動化學院， 哈爾濱　150001; 2.毫米波國家重點實驗室， 南京　210096)

在863計劃新材料領域項目的支持下，中船重工七一二研究所成功研制出我國第一臺1 000 kW高溫超導電動機,2012年4月實現滿功率穩定運行。2012年7月，863計劃“1 000 kW高溫超導電動機”課題通過技術驗收[1]。這標志著我國已經具備了兆瓦級高溫超導電機設計、制造能力，成為國際上少數幾個掌握高溫超導電機關鍵技術的國家之一。但目前針對高溫超導電機的研究較少，在電機的配套系統開發方面進展也十分緩慢，尤其是針對高溫超導電機的勵磁系統方面[2]。國外對高溫超導電機的研究十分重視，美、德、日、韓等國采取一系列措施，完善體制，增加研究經費，制定研發計劃，取得了重大突破。目前針對高溫超導電機勵磁系統的研究主要有以下幾個難點：① 高溫超導電機在設計和運行數據方面尚屬于機密狀態，對電機本體的工作狀態研究開展困難；② 在勵磁系統實際設計方面同樣存在相應問題，由于高溫超導電機的具體設計結構并未具體給出，對于勵磁系統的硬件設計無法做到具有針對性。而對于勵磁系統而言，控制策略決定了系統在穩定和故障狀態下的工作性能，提高勵磁系統的控制性能，對同步發電機和電力系統的安全穩定運行都有重要意義。勵磁控制的作用十分重要，無論是系統工作在正常狀態或是發生故障，勵磁系統控制策略都不可或缺。勵磁系統的性能對于高溫超導電機的運行起著關鍵作用，對于幾個關鍵技術指標如可靠性、穩定性以及電能質量等都有著重要影響。常規的PID控制策略結構簡單，容易實現，并且具有一定的魯棒性，能夠滿足一般精度要求。隨著電力系統的發展，電力系統具有高度非線性、時變性，被控對象用常規PID勵磁已經無法滿足現代電力系統的要求,因此尋找更有效的控制方法。

1　高溫超導電機勵磁系統建模

高溫超導電機勵磁系統構成如圖1所示。其中勵磁系統部分由電力系統穩定器、旋轉整流器和控制部分組成，控制策略將在后面的章節中進行具體設計分析。在勵磁系統之外，輸入為外部加入的給定，然后輸出至高溫超導電機轉子繞組中。下面對各個部分的模型進行建模。

圖2為高溫超導電機勵磁系統原理圖，現根據此原理圖對旋轉整流器和電力系統穩定器部分進行建模設計。

1.1　旋轉整流器數學模型

整流器的工作原理是根據二極管的特性即單向導電特性來決定的。交流輸入、直流輸出的工作方式是確保在同一時間內共陰與共陽這兩組二極管之中只有一個二極管是導通的，共陰二極管中陽極電勢最高的導通，而共陽二極管中陰極電勢最低的導通，剩余的二極管都受非正向的電壓因而不導通[3]。在電路中有負載時，通過不斷變換導通的順序，實現了整流，換流發生了6次，有6個換流點，整流橋輸出的直流電壓為線電壓的包絡線，一個周期中有6個均勻的波頭，每60°間隔的負載電流的平均值是相同的，相應的負載電壓平均值也是相等的，即

(1)

(2)

其中：u2為高溫超導電機輸出電壓；ud為負載電壓平均值。

當負載是一個大的電感與電阻時，電感可以不會出現波動平穩的輸出電流，電路瞬時負載的電壓波形與當電路負載中只含有電阻時是一樣的，電路負載的電流為常數

(3)

其中時間常數T與整流電路的相數有關[4]。

1.2　電力系統穩定器(PSS)數學模型

在電力系統中，低頻振蕩一直是一個難以解決的問題，為了克服這個問題，科學家們研制了電力系統穩定器，作為一種附加勵磁控制技術來抑制低頻振蕩[5]。它抑制低頻振蕩的方法為在勵磁調節器中，引入附加信號，這個信號要領先于轉速。通過這個信號，可以產生相應的正阻尼轉矩，這個轉矩可以用來調和勵磁調節器在調解中負反饋所產生的負阻尼轉矩。在PSS工作過程中，除了轉速信號，它還需要對其他與振蕩相關的信號進行采樣，例如有功功率和頻率，對采集的信號進行處理后同樣融入之前所產生的信號中，可以對負阻尼信號進行更為有效的中和。

而輸入信號方面，雖然可以對以上所提及的信號進行全面采樣，但這樣做的復雜性較高，不利于工業生產，故不同國家對于輸入信號的選擇不同[6]。有些國家，例如日本，采用ΔP作為輸入量，而采用Δω即轉速作為輸入量的國家更多一些，例如美國。本文為了增加PSS的調節精度，決定同時選擇ΔP和Δω作為輸入量，電力系統調節器的數學模型如圖3所示。

高溫超導電機模型較為復雜，在此不詳細給出，在仿真時將會采用相應的數學模型進行仿真。

2　勵磁系統模糊PID控制策略設計與仿真

2.1　勵磁系統模糊PID控制策略設計

PID控制策略的工作原理十分簡單，也有其固有的缺陷。首先，PID算法的控制對象主要針對線性系統，對系統精確化建模要求較高，對于復雜系統往往控制效果較差；其次，由于放大器的飽和現象，會導致PID控制策略不得不對其微分信號進行削弱，同時由于被控對象的參數不斷變化，而控制效果將會大打折扣；最后，傳統PID算法對系統負載變化或是對干擾影響的自適應能力弱[7]。因此，傳統的PID控制策略只適用于低負載、低非線性、擾動較小的情況，已經無法滿足現代電力系統的要求，故本文提出了模糊PID勵磁控制策略。

高溫超導電機勵磁系統的模糊PID勵磁控制策略是以發電機的機端電壓與給定值的偏差和偏差變化作為反饋信號，通過模糊邏輯規則推理出相應的控制信號，作用于高溫超導電機上，實現對高溫超導電機的勵磁控制作用[8]。

作為一種自適應PID控制算法，模糊PID的特點在于在常規PID的基礎之上加入了模糊推理算法。模糊控制不依賴精確的數學建模，對控制對象的線性化程度要求較低，而且還能有效的抗干擾，具有良好的自適應性和魯棒性[9]。模糊PID控制算法將常規PID控制算法與模糊控制算法的優良性能相結合，是一種高效的智能PID控制算法[10]。

模糊推理系統(fuzzy system)的原理流程如圖4所示。

本文設計的勵磁控制系統，輸入的量是端電壓與期望值的偏差e，以及誤差變化率e′。這兩個量是具有物理意義的量，它們都有自身的變化范圍，這個變化范圍被稱為系統的基本論域。被控對象所要求輸出變量u的參數的變化范圍為精確值，變化范圍被稱為模糊控制策略輸出變量的基本論域。模糊化的第一個步驟就是將這兩個實際輸入變量模糊化以及將輸出變量模糊化[11]。

輸入e、ec分別表示模糊控制策略輸入的端電壓誤差和端電壓誤差變化率；輸出Δkp、Δki、Δkd分別為經過模糊控制策略處理得到的3個PID參數變量，其中Δkp為PID比例因子的整定增量，Δki為PID積分因子的整定增量，Δkd為PID微分因子的整定增量；u為模糊PID控制策略輸出的控制量。

保留PID算法的設計則，只需要對模糊控制策略模塊進行建模設計。該模糊控制策略為兩輸入單輸出模型，設計步驟按照模糊控制策略原理如下：

1) 模糊量化

輸入e、ec和輸出Δkp、Δki、Δkd的模糊子集設為：NB,NM,NS,ZO,PS,PM,PB

分別表示：“負大”，“負中”，“負小”，“零”，“正小”，“正中”，“正大”。

確定e的論域為[-0.3，0.3]，隸屬度函數選擇高斯型；ec的論域為[-0.1，0.1]，隸屬度函數選擇高斯型；Δkp的論域為[-1，1]，隸屬度函數選擇三角型，Δki的論域為[-0.1，0.1]，隸屬度函數選擇三角型；Δkd的論域為[-0.05，0.05]，隸屬度函數選擇三角型。模糊系統中的核心為知識庫，而知識庫的核心則為模糊規則，模糊規則是用來對輸入與輸出之間的模糊數學制定邏輯關系的。模糊規則的獲取主要有兩種方法：一種與PID 控制策略參數設定類似，為經驗法，另一種為測試法。本文的模糊規則是利用 PID 算法參數調整的工程設計經驗，并結合專家知識和實踐中的控制經驗加以總結而制定的，其制定原則是保證系統具有最佳的動靜態性能。

2) 模糊PID控制量

輸出模糊量反模糊化后得到整定好的 PID 修正參數，代入 PID 控制策略得到新的PID 3個環節參數為：

Kp=ΔKp+Kp0

Ki=ΔKi+Ki0

Kd=ΔKd+Kd0

(4)

式中，Kp0、Ki0、Kd0為初始PID參數值。模糊PID控制量規則見表1。

表1　模糊PID控制量規則

利用PID控制算法公式，得到模糊PID控制量如式(5)所示

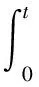
(Δkd+Kd0)ec(t)

(5)

2.2　勵磁系統模糊PID控制策略下仿真

上文所設計的模糊控制策略，模糊PID中Kp、Ki、Kd3個值并不是固定值，所以在構建仿真子系統時無法像普通PID一樣將3個值作為固定值，而是需要將這3個值作為輸入值進行處理。同時，模糊控制策略中不僅需要端電壓誤差e這一個輸入量，同時也需要端電壓誤差變化率ec作為另一個輸入量[12]。模糊PID控制策略仿真模型如圖5所示。圖5中，Ke和Kec分別為模糊控制策略中的輸入值。

仿真時間定為10 s，算法設置為ode23tb。PID控制策略控制下，設置幾個控制參數分別為：Kp=20，Ki=4.2，Kd=0.21，隨后設置模糊控制策略，將量化因子設置為Ke=3、Kec=1；比例因子設置為Kup=26、Kui=1、Kud=10。常規工作狀態仿真結果如圖6所示。

之前本文所設計的仿真模型都是針對高溫超導電機在正常工作狀態下的，而在正常工作狀態下會發生很多無法預知的突發狀況，這些也是勵磁系統需要面對的問題。在正常工作狀態下，電機有時需要面對輸出端短暫短路的情況，在本研究中，通過模擬端電壓出線端短路來測試勵磁系統在面對故障時的調節效果。短路的模擬方式如圖5所示，通過在無窮大電網上添加三相短路故障模塊來模擬短路故障。故障時間設為從15 s到15.1 s，仿真時間設為20 s，其他參數設置與常規工作狀態下參數相同。故障狀態下端電壓和勵磁電壓的仿真曲線如圖7、圖8所示。

3　勵磁系統變論域模糊PID控制策略設計與仿真

3.1　勵磁系統變論域模糊PID控制策略設計

模糊控制策略所推出的算法中，難免具有一定的非線性成分，這是由于模糊規則的復雜，會降低控制效果；控制精度取決于控制規則數量、隸屬度函數選擇及專家經驗，系統調試復雜。模糊控制具有較強的魯棒性，自適應能力差，而變論域模糊控制則有效地對其進行了改進。

對于變論域的模糊控制策略的設計不需要太多的領域專家知識，只要知道規則的大致趨勢；相比模糊控制策略對控制規則、隸屬度函數和等距劃分沒有特別高的要求，系統設計更為簡單，精度也更高[13]。所以，變論域模糊控制是一種高精度的模糊自適應算法，能夠有效地應對控制對象的非線性、難以建模和模型參數變化的難點。圖9為常見的變論域模糊控制原理框圖。

變論域即是輸入輸出論域隨著兩個輸入變量參數的變化而變化，將輸入輸出論域變化表示為如式(6)：

X1(x)=[-α(x)E,α(x)E]

X2(x)=[-β(x)Ec,β(x)Ec]

Y(x)=[-γ(x)U,γ(x)U]

(6)

式中：X1(x)、X2(x)、Y(x)為變論域；α(x)、β(x)、γ(x)分別為輸入變量e、ec、輸出變量u的論域伸縮因子，大小與輸入變量e、ec有關，表示為函數形式。這就是所謂的變論域，即實現了論域隨誤差的變化而變化。以輸出論域為例，其論域伸縮情況如圖10、圖11所示。由圖可知，變論域的核心也就是伸縮因子的選取，伸縮因子的大小變化決定了論域變化后的形狀，更是直接影響變論域模糊的控制性能[14]。

對于伸縮因子的選取，基于數學模型的伸縮因子方法是通過伸縮因子的定義和性質，將伸縮因子表示成輸出變量的函數，常用的輸入輸出論域伸縮因子的函數模型如式(7)：

(7)

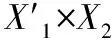
本系統的模糊控制通過計算機處理器來實現，為了便于在其他控制策略上移植，選擇采用離散時間系統進行控制策略設計。給定初始控制規則R(0)=R，初始論域X1=[-E,E]，X2=[-EC,EC]，Y=[-U,U]上的線性基元組分別為{Ai}(1≤i≤p)， {Bj}(1≤j≤q)， {Cij}(1≤i≤p, 1≤j≤q)，峰值點滿足

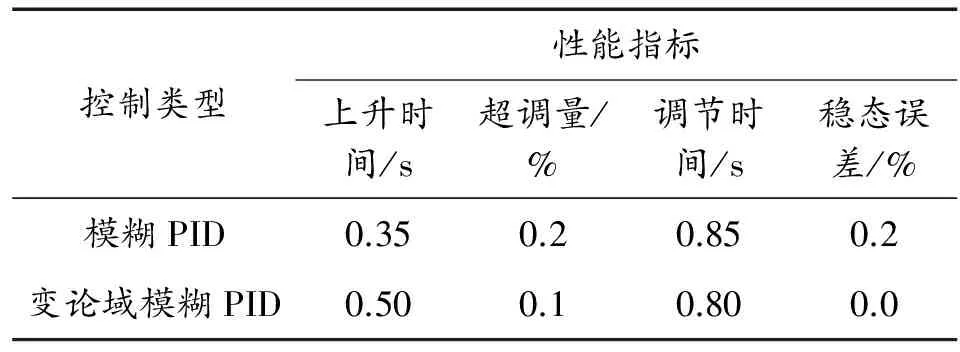
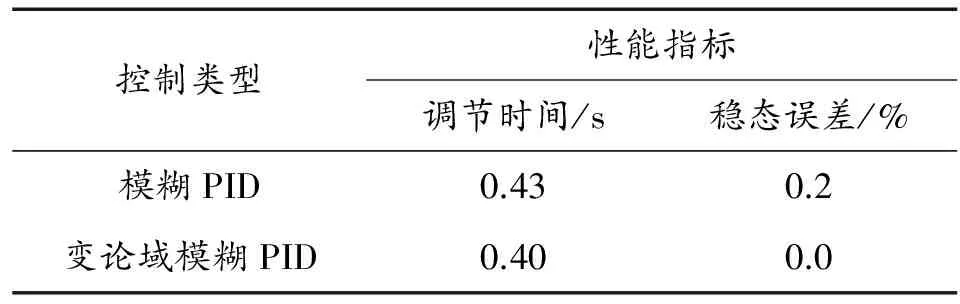
-EC=x21

-E=x11

令x1i(0)=x1i，x2j(0)=x2j，yij(0)=yij，-U∈=y11

步驟1：初值輸入x1(0)∈X1,x2(0)∈X2，得到輸出：

y(1)=Fx10,x20=

(8)

步驟2：y(1)施加對象后得到系統輸出，反饋給系統參考輸入相比較，得到控制策略的輸入x1(1),x2(1)。令：

x1i(1)=α(x(1))x1i(0)

(9)

x2j(1)=βx1(1),x2(1)x2j0

(10)

yij(1)=F(x1i(1),x2j(1))=

(11)

y(2)=F(x1(1),x2(1))=

(12)

步驟k：y(k)施加對象后得到系統輸出，反饋給系統參考輸入相比較，得到控制策略的輸入x1(k),x2(k)，同理，有：

x1i(k)=α(x1(k))x1i(0)

(13)

x2j(k)=βx1(k),x2(k)x2j0

(14)

yij(k)=F(x1i(k),x2j(k))=

(15)

yij(k+1)=F(x1(k),x2(k))=

(16)

綜合以上步驟，得到上述雙輸入單輸出自適應模糊控制策略輸出為：

Asαx1(k)x1i(0)·

Bjx2(k)/βx1(k),x2(k)·

Btβx1(k),x2(k)x2j(1)yst(0)

(17)

此外，當x1(k)→0,x2(k)→0時，y(k+1)→0。

3.2　勵磁系統變論域模糊PID控制策略下仿真

常規工作狀態下仿真結果如圖12所示。

故障狀態下端電壓和勵磁電壓的仿真曲線如圖13、圖14所示。

4　高溫超導電機勵磁系統仿真分析

從兩種控制策略的常規工作狀態仿真曲線圖6與圖12中可以明顯看出在模糊PID控制策略控制下的曲線沒有超調，在經過短暫的抖動后進入穩態，沒有靜態誤差。在變論域模糊控制策略下的勵磁電壓曲線相對普通模糊控制更加平滑，不僅沒有超調，也沒有進入穩態之前的抖動。

表2是兩種控制策略在常規工作狀態下控制策略性能對比。

控制類型性能指標上升時間/s超調量/%調節時間/s穩態誤差/%模糊PID0．350．20．850．2變論域模糊PID0．500．10．800．0

根據表2的數據，可以得到分析結論。在調節時間和穩態誤差以及超調量這幾個方面，雖然模糊PID在上升時間上快于變論域模糊PID，但是從實際的響應曲線中可以看出，模糊PID在進入穩態誤差之前的抖動較大，實際調節時間是要比變論域模糊PID長的。

由此可以確定，變論域模糊控制在常規工作狀態下，控制效果上要優于模糊PID。

在故障狀態下，通過對端電壓的兩個響應曲線圖7與圖13的對比可以看出，在模糊PID控制策略控制下的端電壓響應曲線中電壓的調節時間明顯較長，變論域模糊PID控制調節時間較短，具體性能指標如表3所示。從表3的數據可知，在模糊PID控制下，端電壓的調節時間從開始調節到故障消失端電壓輸出恢復正常花費了0.03 s。兩組波形的對比證明變論域模糊PID的確是相對模糊PID在控制精度和效果上都占優勢。

表3　短路狀態下兩種控制策略端電壓性能指標

在勵磁電壓方面，從圖6與圖12中可看出，模糊PID在進入穩態之前有一個小小的抖動，振蕩兩次進入穩態，但變論域模糊PID則沒有這方面的問題，同時從圖8與圖14中可以看出，在勵磁電壓響應方面變論域模糊PID的精確度更高，進入穩態比較平滑。具體性能指標如表4所示。

表4　短路狀態下兩種控制策略勵磁電壓性能指標

通過表4的數據可以分析出，在短路狀態下，變論域模糊PID的調節時間比模糊PID的調節時間快0.03s，并且變論域模糊PID沒有穩態誤差，所以無論是在調節時間還是穩態誤差上，變論域模糊PID控制都在控制性能上有著絕對的優勢。

5　結論

本文利用模糊控制理論，根據勵磁系統的控制要求和特點，結合傳統PID和變論域控制的優點，構建了一種變論域模糊PID控制策略。因為模糊控制不需要有精確的系統數學模型，所以基于模糊理論構建的勵磁調節器具有更廣泛的調節范圍。仿真實驗結果表明：變論域模糊PID控制在調功、調壓和大擾動時具有更好的控制精度、反應速度和抗干擾能力，能夠有效改善系統各狀態量及輸出量的動、靜態性能，提高系統的穩定運行能力。

參考文獻：

[1]趙朝會,李進才.超導發電機的研究現狀及發展前景[J].上海電機學院學報,2013(6):314-321.

[2]賀徽,周建中,譚建華,等.基于Mamdani模糊PID的同步發電機勵磁控制[J].華中科技大學學報(自然科學版),2010(2):34-37.

[3]ESTEBAN A,DEVAIAH N,PANAGIOTIS L,et al.Methodology to assess the performance of an aircraft concept with distributed propulsion and boundary layer ingestion using a parametric approach[J].Proceedings of the Institution of Mechanical Engineers Part G-Journal of Aerospace Engineering,2015,229(4):682-693.

[4]WOLFGANG N,JOERN G,JOACHIM F.Test results from siemens low-speed,high-torque HTS machine and description of further steps towards commercialisation of HTS machines[J].Physica C:Superconductivity and Its Applications,2012,482:105-110.

[5]劉勝,張玉廷,余辰光.船舶電力推進系統電機組三維模糊控制[J].中國電機工程學報,2012,32(3):117-123.

[6]劉子全,高磊,趙嫻,等.一種可有效提高臨界增益的改進型電力系統穩定器[J].中國電機工程學報,2015,35(8):1875-1881.

[7]IOAN F,IOSIF S.Adaptive fuzzy PI controller with shifted control singletons[J].Expert System with Applications,2016,54:1-12.

[8]韓兵,周臘吾,陳浩,等.基于變論域模糊控制的大型風電機組偏航系統[J].電工電能新技術,2016,35(8):15-20.

[9]MIER L.A,BENITEZ J.S,LOPEZ R,et al.Adaptive fuzzy control system for a squirrel cage induction motor[J].IEEE Latin America Transactions,2017,15(5):795-805.

[10] A-RONG K,KWANG-MIN K,HEECHEOL P,et al.Performance analysis of a 10 kW superconducting synchronous generator[J].IEEE Transactions on Applied Superconductivity,2015,25(3):1-4.

[11] CHEN QING,NAN YU-RONG,ZHENG HENG-HUO,et al.Full-order sliding mode control of uncertain chaos in apermanent magnet synchronous motor based on a fuzzy extended state observer[J].Chinese Physics B,2015,24(11):161-166.

[12] KARMAKER H,SARANDRIA D,HO M T,et al.High-Power dense electric propulsion motor[J].IEEE Transactions on Industry Applications,2015,51(2):1341-1347.

[13] 崔家瑞,李擎,張波,等.永磁同步電機變論域自適應模 糊PID控制[J].中國電機工程學報,2013,33(S1):190-194.

[14] 李紅偉.變論域模糊控制的無刷直流電機控制系統[J].控制工程,2010,17(5):599-602.