基于粒子群優化的卡爾曼濾波去耦算法

陸志毅, 李相平, 陳　麒, 鄒小海

(海軍航空工程學院電子信息工程系, 山東 煙臺 264001)

0　引　言

隨著作戰的電子環境日趨復雜,捷聯導引頭技術受到各個軍事強國的重視。捷聯導引頭相比于傳統的導引頭具有可靠性高、質量輕以及彈體過載信息不敏感[1]等優勢,尤其是相控陣雷達導引頭。近年來,美國戰略防御局、英國的Qinetiq公司以及意大利的Matra Bae Dynamics Alenia (MBDA)公司都在積極地攻克相控陣雷達導引頭彈體姿態擾動和波束指向耦合的難題[2]。針對相控陣雷達導引頭去耦的問題,文獻[3]分析了波束角指向誤差斜率的特性,并提出了基于波束角誤差補償的解耦算法;文獻[4-5]根據波束指向在慣性坐標系下不變的原理,提出了通過坐標轉換的關系實時保持波束穩定的算法;文獻[6-10]研究了卡爾曼濾波器在相控陣雷達導引頭去耦以及彈目視線角速率提取上的運用,但是在濾波過渡的過程中,由于導引頭前向通道增益系數Ks和波束控制增益系數Kg刻度尺度不同帶來的隔離度問題,會引起整個制導系統的不穩定,使得提取的視線角速率誤差過大。

由于制導系統是一個非線性、連續的系統,在建立卡爾曼濾波方程的時候,可以根據擴展卡爾曼濾波(extended Kalman filter, EKF)采用泰勒級數展開一階近似的方法將非線性系統線性化的基本思想[11]進行處理,然后把連續型卡爾曼濾波方程離散化即可。

本文提出了一種粒子群優化的卡爾曼濾波去耦算法,對于導彈制導回路中的非線性系統參數,采用EKF進行處理,根據狀態方程和量測方程獲得最小均方差意義下的最優估計[12]。同時為了減小Ks和Kg帶來的影響,利用粒子群優化算法不斷對Ks和Kg值進行調整,使得經過濾波后的估計值達到最優值。最后通過仿真實驗對比了優化后的彈目視線角速率提取值誤差和未優化的提取值誤差,以及優化后算法和當前主流的波束誤差補償算法的誤差值。表明了所提算法可以克服Ks和Kg帶來的誤差量過大問題,并且驗證了算法在相控陣雷達導引頭上去耦的有效性。

1　粒子群優化的EKF去耦算法原理

EKF可以根據系統每個時刻的量測值和濾波參數,通過量測方程和狀態方程進行時間更新和量測更新,進而得到該系統狀態的后驗估計值。同時用粒子群算法修正輸入的增益參數Ks和Kg,直至輸出的結果滿足適應度函數條件,即為最優的估計值。圖1為整個去耦算法的原理框圖。

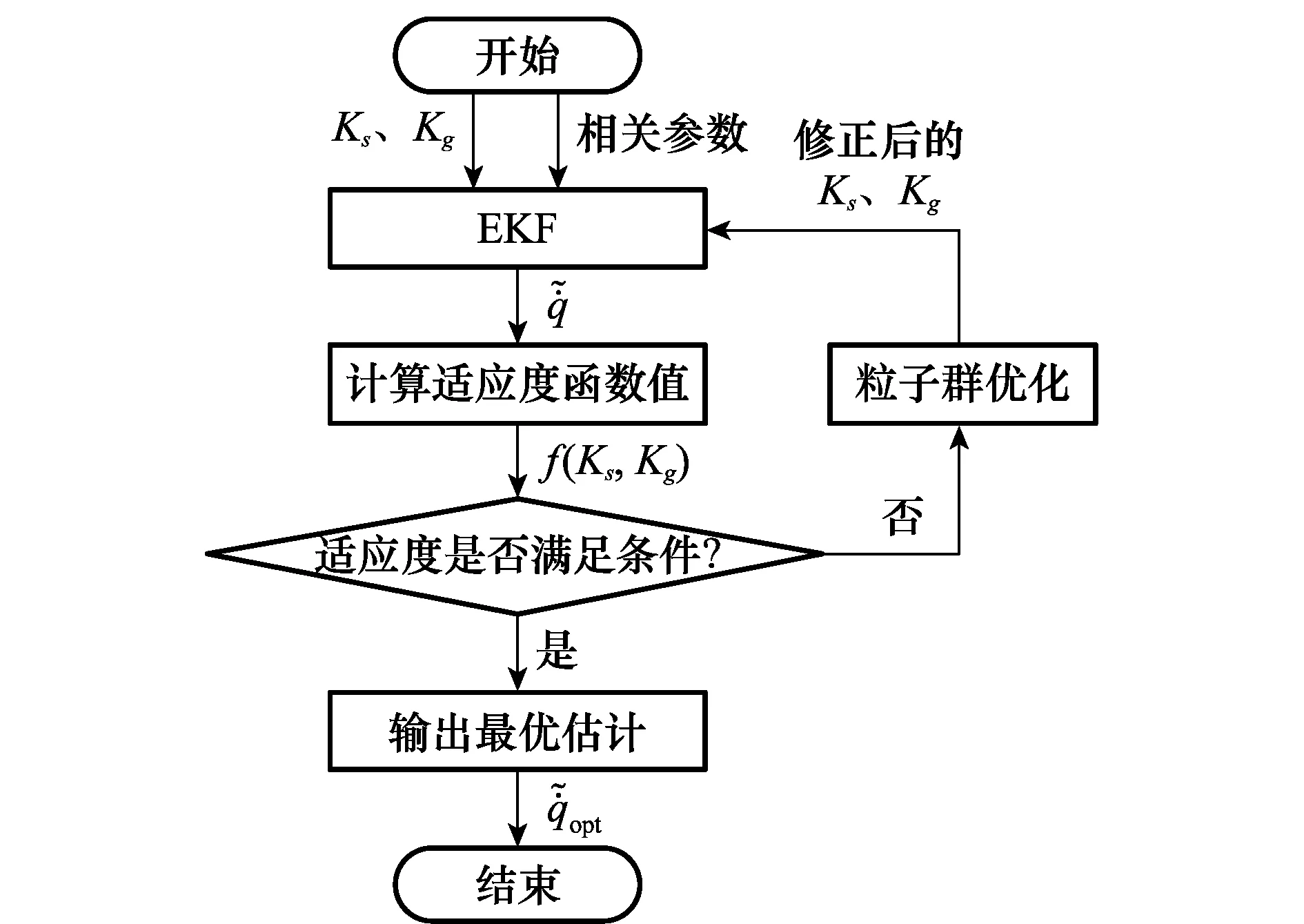
圖1　粒子群優化的EKF去耦算法原理框圖

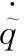
2　粒子群優化EKF去耦算法的實現

2.1　粒子群優化算法

粒子群優化是由Kennedy和Eberhart基于一種社會心理學模型中的社會影響和社會學習而提出的。其仿真模型是要模擬鳥群在捕食過程中,避免碰撞,通過團體的協作,不斷調整自己的飛行軌跡向最優位置靠近的行為[13]。針對問題中提到優化增益參數Ks和Kg,可以用每個粒子代表一個2維空間的候選解,選擇合適的適應度函數,計算各個粒子的適應度,并按照式(1)和式(2)來不斷地迭代和更新自己的速度和位置。

vij(t+1)=ωvij(t)+c1r1j[pbest-xij(t)]+

c2r2j(t)[gbest-xij(t)]

(1)

xij(t+1)=xij(t)+vij(t+1)

(2)

式中,vij和xij分別是粒子i在第j維上的速度和位置;pbest為粒子i遍歷后在空間搜索的個體最優位置;gbest是所有粒子目前為止搜索到的全局最優位置;t表示當前的時間;c1和c2相當于粒子的加速度,一般取正數;r1,j和r2,j是區間[0,1]之間的隨機數,主要是把不確定的因素迭代到算法中,增大算法的隨機性;ω為慣性權重,用來衡量上個時刻的速度對于粒子下次運動的影響。

在粒子群優化算法中一個重要的指標就是適應度函數,其不僅可以約束粒子的運動,還能有效地作為目標函數終止粒子的更新[14]。如果選擇的不合適可能會導致算法早熟收斂,使得結果陷入局部最優解,最后通過EKF后達不到最優的狀態后驗估計值。結合EKF的目的是要減小測量過程中的觀測噪聲影響[15],可以將真實值和濾波后的估計值之間的均方誤差作為適應度函數,記作

(3)

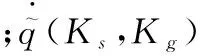
2.2　EKF去耦算法過程實現

對于卡爾曼濾波而言,可以從與被提取信號相關的量測信號中應用算法對需要的信號做出最優估計。其處理的對象一般是由高斯白噪聲引起的隨機響應,并且系統的白噪聲和量測過程中的白噪聲不是卡爾曼濾波濾除的對象。實質上相當于一整套遞推的算法,在一個濾波周期內主要包含了時間更新和量測更新的過程,其計算回路和更新過程的框圖如圖2所示。

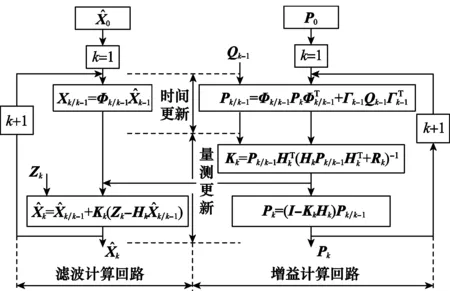
圖2　卡爾曼濾波的計算回路和更新過程

根據圖3所示相控陣雷達導引頭制導跟蹤回路,可以選取合適的狀態變量和量測量,寫出EKF的基本濾波方程,從而建立EKF去耦算法的模型。

圖3　相控陣雷達導引頭制導跟蹤回路

為了達到去耦和提取彈目視線角速率的目的,可以選擇式(4)系統變量作為狀態變量。

(4)

系統的量測量選取為

(5)

該系統的系統方程和量測方程為

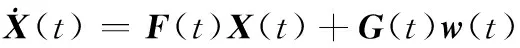
Z(t)=H(t)X(t)+v(t)

(6)

其中

(7)

對式(8)進行離散化處理,取步長為Δt,進而得到狀態轉移矩陣為

Φk/k-1=I+F(t)Δt=

(8)

根據圖3系統變量之間的關系,可以計算出

(9)

離散化處理后量測矩陣為

(10)

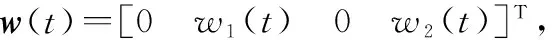
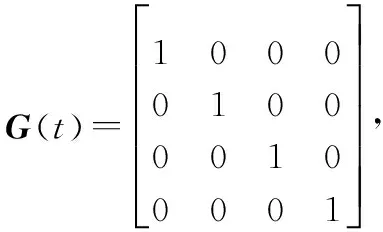
(12)

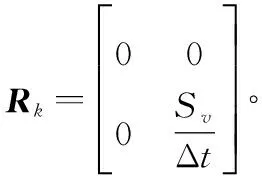
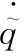
3　粒子群優化的EKF去耦算法驗證

3.1　粒子群優化的作用

導引頭前向通道增益Ks和波束控制增益Kg作為相控陣導引頭制導控制回路中影響EKF估計彈目視線角速率的重要參數,對這兩個參數進行粒子群優化組合,可以極大地提高后驗估計值的精度。并且將優化后的參數組合作為工業生產時的一個重要參考標準,可以適當減小導彈姿態擾動對波束指向的影響。

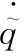
3.2　仿真結果與性能分析

運用粒子群優化參數的一個重要參考就是適應度,在本算法中優化參數是二維的,所以所選粒子的維數也為2,分別表示Ks和Kg。考慮到彈上嵌入式計算機的工作能力,為了防止粒子數選取過大帶來的計算時長問題,粒子數取40,一定程度上既能保證不陷入局部最優,也能使計算時間控制在一個能夠接收的范圍[16-17]。由于在本算法中選取的適應度函數表示均方誤差值,典型的線性遞減慣性權重在初期雖然全局的搜索效果很好,但是隨著其值的減小容易陷入局部最優,不利于尋找最優解[18-19],所以選取固定的慣性權重值,參考文獻[20-21]推薦的固定權重ω1=0.6。在加速度因子選取上主要參考文獻[22]給出的常數值c1=c2=1.5。算法最大迭代次數為500次,避免因為沒有找到最優解而陷入死循環。在導彈跟蹤的過程中,為了可以有效地輸出視線角速率信息,提高導彈的命中精度,需要控制俯仰方向上的角速率誤差幅值在0.05°/s以內,偏航方向上的誤差幅值在0.1°/s以內,此時對應的適應度值約為0.006 4,所以可將適應度滿足條件設定為不超過10-3。EKF算法中功率譜取Sw1=Sw2=0.002 W/Hz,Sv=0.03 W/Hz時,對Ks和Kg的適應度進行仿真,圖4為適應度與迭代次數的曲線圖。

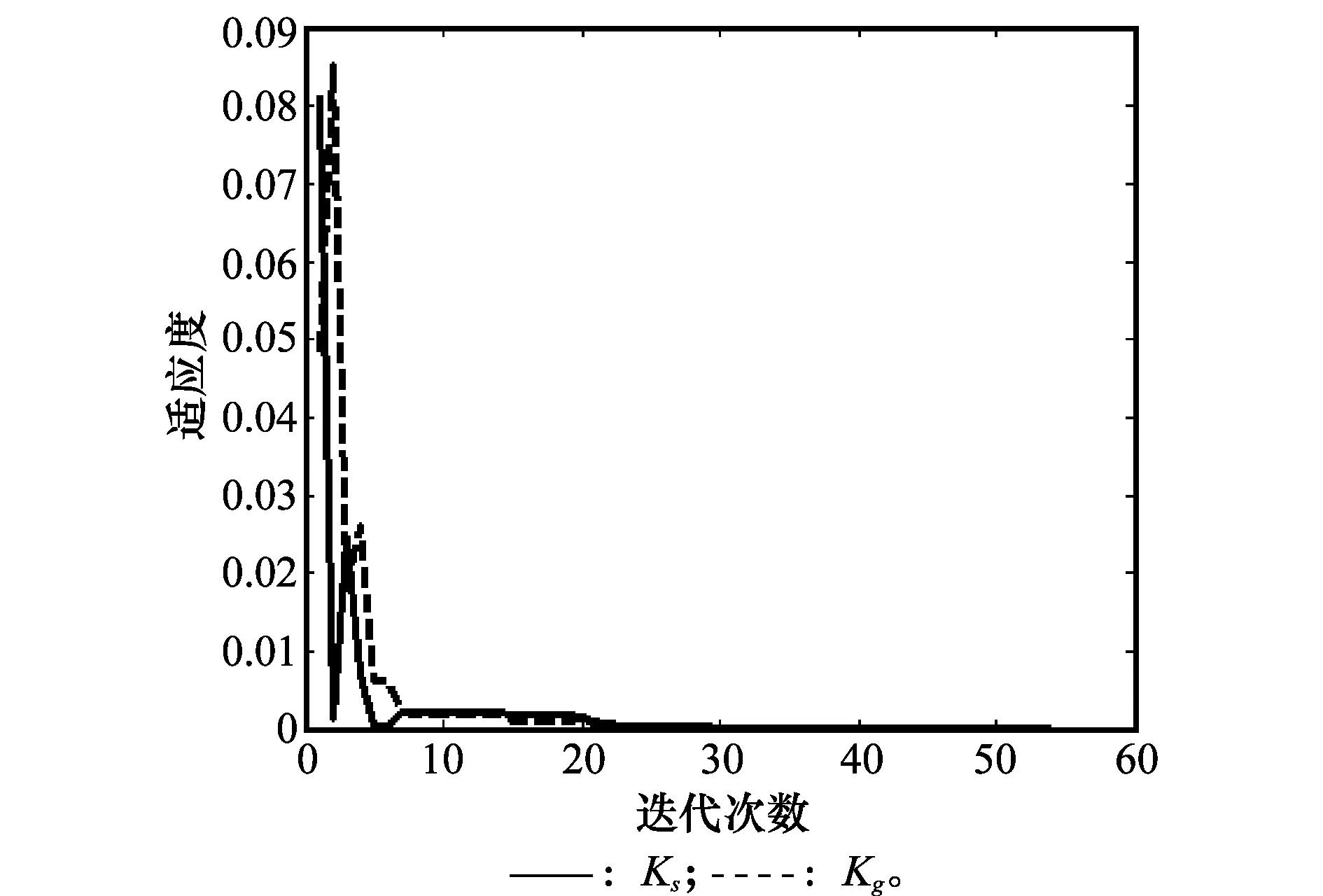
圖4　適應度與迭代次數曲線圖

可見當粒子群迭代到23次左右時,Ks和Kg的值達到符合條件的最優解,此時的適應度約為6.001 24×10-4,其實際的意義就是經過EKF濾波后真實值與估計值的均方差值,表明此時所得到的估計是最優的后驗估計值。其對應的Ks和Kg值分別為10.863和1.024,考慮到工業設計的實際,取前向通道增益Ks為10,波束控制增益Kg為1。計算此時的適應度值為6.113 25×10-4,與調整前的適應度誤差在10-3～10-4,由于適應度滿足的條件為不超過10-3,所以調整后的值是可取的。

確定濾波參數Ks和Kg后,通過EKF進行去耦和視線角速率的提取。由于在實際的導彈飛行中滾動姿態趨于穩定,因此在仿真時不考慮滾動角帶來的影響。設定仿真條件為

式中,φ、?、γ分別是導彈姿態的俯仰角、偏航角和滾動角;qy和qz是真實的俯仰方向和偏航方向的彈目視線角;fm一般取3 Hz。

選取兩個增益Ks和Kg分別為10和1,經過EKF濾波后提取俯仰和偏航兩個方向的視線角速率,計算此時的誤差值,給出粒子群優化EKF去耦算法估計誤差值圖,如圖5所示。同時在Ks=20,Kg=1.1的條件下得到常規EKF視線角速率提取值誤差圖如圖5所示。在相同的仿真條件下給出當下主流的波束誤差補償去耦算法的誤差值圖,如圖5所示。對比波束誤差補償算法的誤差值和粒子群優化后EKF去耦算法的誤差值發現,在相控陣雷達導引頭去耦上,優化后的算法更具有優勢。

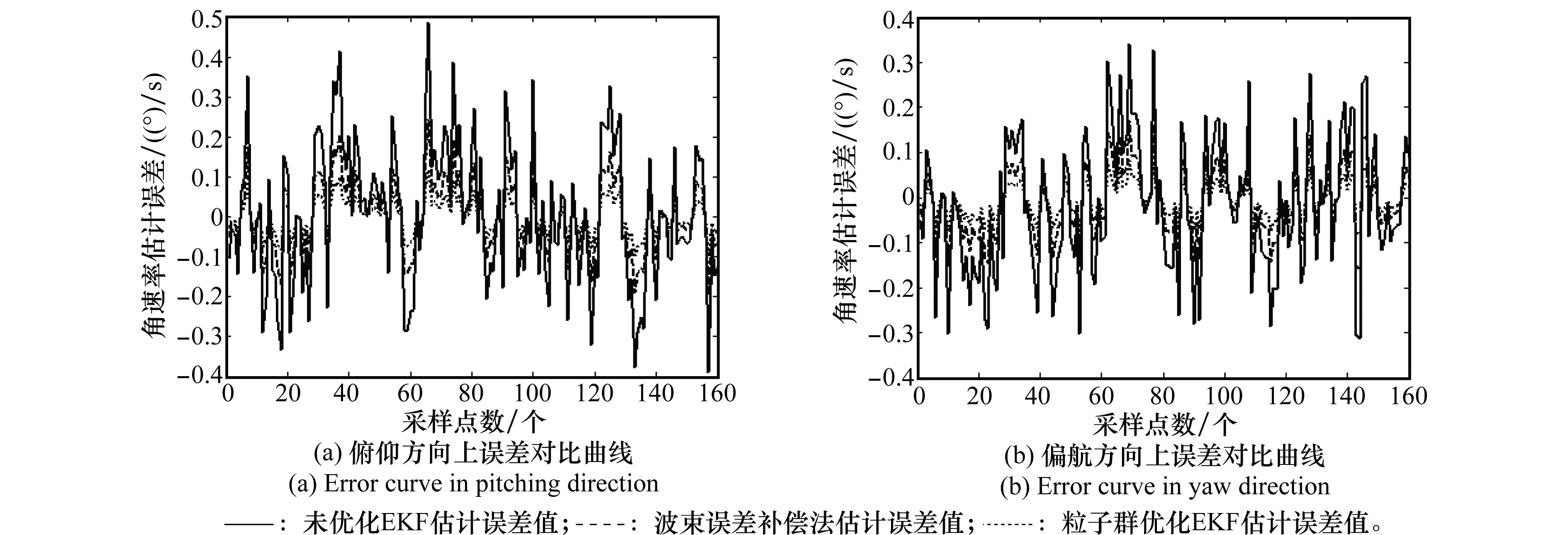
圖5　3種算法視線角速率提取值的誤差曲線

為了更清晰地表征算法的優良性,表1給出了Ks=10時不同Kg對各誤差以及適應度的影響情況,表2給出了Kg=1時不同Ks對各誤差以及適應度的影響情況。

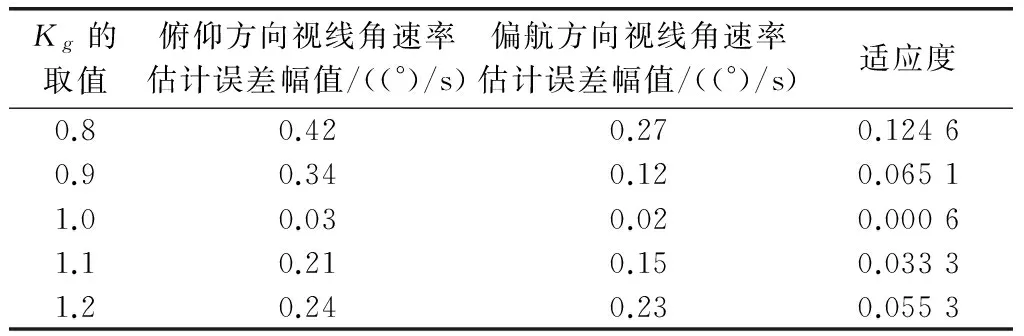
表1　Ks=10時不同Kg對各誤差以及適應度的影響情況

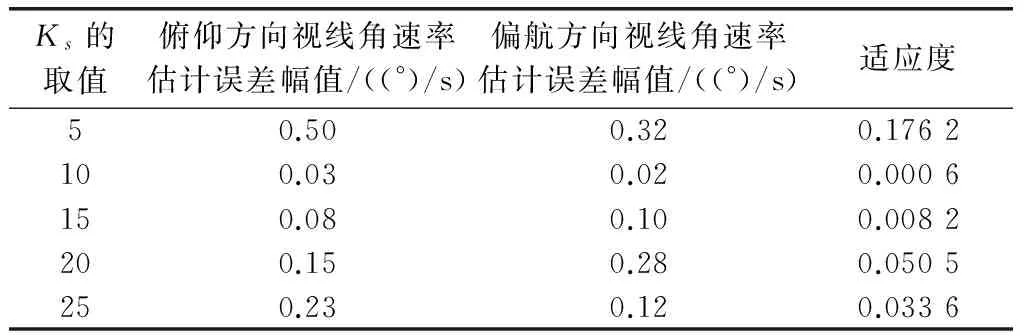
表2　Kg=1時不同Ks對各誤差以及適應度的影響情況

由圖5可知,雖然常規的EKF去耦算法在提取視線角速率上擬合性較好,但是沒有粒子群優化后的EKF算法的精度高。尤其是通過表1和表2對比發現,不同的Ks和Kg組合所導致提取視線角速率的誤差值和適應度也相差很大,可以認為Ks和Kg是不相關的兩個增益參數[23],因此當Ks=10和Kg=1時,EKF提取值效果最好,同時也驗證了粒子群優化得到參數的準確性。

4　結　論

首先通過粒子群優化的EKF算法對導引頭前向通道增益Ks和波束控制增益Kg進行優化組合,然后進行濾波,使得視線角速率的提取值誤差控制在一個較小的范圍內,不僅有效地解決了因Ks和Kg取值不當引起誤差值過大的問題,而且提高了彈目視線角速率提取值的精度。最后仿真結果表明,在系統不同的增益條件下,隔離彈體擾動的程度也有很大的差別,這為實際工程中設計相控陣雷達導引頭前向通道增益Ks和波束控制增益Kg提供了重要的理論依據和參考價值。

參考文獻：

[1] 賈鑫,羅艷偉,羅麗.全捷聯導引頭解耦技術方法[J]. 戰術導彈技術, 2013, 34(1): 77-81.

JIA X, LUO Y W, LUO L. Research on decoupling methods of strapdown seeker[J].Tactical Missile Technology,2013,34(1): 77-81.

[2] ROCK J C, MULLINS J H, BOOTH J P. The past, present, and future of electronically-steerable phased arrays in defense applications[C]∥Proc.of the IEEE Aerospace Conference, 2008: 1-7.

[3] 魯天宇,尹健,夏群利,等.基于波束角誤差補償的相控陣導引頭解耦算法[J].系統工程與電子技術,2015,37(9):2123-2128.

LU T Y, YIN J, XIA Q L, et al. A kind of decoupling algorithm of phased array seeker based on beam angle error compensation[J]. Systems Engineering and Electronics, 2015, 37(9): 2123-2128.

[4] 樊會濤,楊軍,朱學平.相控陣雷達導引頭波束穩定技術研究[J].航空學報,2013,34(2): 387-392.

FAN H T, YANG J, ZHU X P. Research on beam stable technology of phased array radar seeker[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(2): 387-392.

[5] 李秋生.相控陣雷達導引頭捷聯去耦技術研究[J]. 制導與引信, 2005, 26(2): 19-22.

LI Q S. Strapdown decoupling technique research on phased array radar seeker[J]. Guidance and Fuze, 2005, 26(2): 19-22.

[6] ELGAME S A, SORAGHAN J. Target tracking enhancement using a Kalman filter in the presence of interference[C]∥Proc.of the Geoscience and Remote Sensing Symposium,2009:681-684.

[7] ROTSTEIN H, REINER J, BEN-ISHAI A. Kalman filter mechanization in INS/Seeker fusion and observability analysis[C]∥Proc.of the AIAA Guidance, Navigation, and Control Conference and Exhibit, 2001: 2001-4402.

[8] VERGEZ P L, MCCLENDON J R. Optimal control and estimation for strapdown seeker guidance of tactical missiles[J]. Journal of Guidance, Control,and Dynamics,1982,5(3):225-226.

[9] YUN J, RYOO C K, SONG T L. Strapdown sensors and seeker based guidance filter design[C]∥Proc.of the International Conference on Control, Automation and Systems, 2008: 468-472.

[10] CHEN J, LI J H, YANG S H, et al. Weighted optimization-based distributed Kalman filter for nonlinear target tracking in collaborative sensor networks[J]. IEEE Trans.on Cybernetics, 2017, 47(11): 3892-3905.

[11] 宗睿. 導引頭天線罩誤差及相控陣導引頭波束指向誤差在線補償方法研究[D]. 北京: 北京理工大學, 2016.

ZONG R. Research on online compensation methods for radome error of seeker and beam direction error of phased array seeker[D]. Beijing: Beijing Institute of Technology, 2016.

[12] 張旭輝,林海軍,劉明珠,等.基于蟻群粒子群優化的卡爾曼濾波算法模型參數辨識[J].電力系統自動化,2014,38(4):44-49.

ZHANG X H, LIN H J, LIU M Z, et al. Model parameters identification of UKF algorithm based on ACO-PSO[J]. Automation of Electric Power Systems, 2014, 38(4): 44-49.

[13] YANG G, ZHOU F R, MA Y, et al. Identifying lightning channel-base current function parameters by powell particle swarm optimization method[J]. IEEE Trans.on Electromagnetic Compatibility. 2017, 60(1): 182-187.

[14] LI J, ZHANG J Q, JIANG C J. Composite particle swarm optimizer with historical memory for function optimization[J]. IEEE Trans.on Cybernetics, 2015, 45(10): 2350-2363.

[15] 秦永元,張洪鉞,汪叔華.卡爾曼濾波與組合導航原理[M].3版.西安:西北工業大學出版社, 2015.

QIN Y Y, ZHANG H Y, WANG S H. Kalman filtering and integrated navigation principle[M]. 3rd ed. Xi’an: Northwestern Polytechnical University Press, 2015.

[16] WANG L, YANG B, ORCHARD J. Particle swarm optimization using dynamic tournament topology[J]. Applied Soft Computing, 2016, 48(16): 584-596.

[17] SARKER R A, ELSAYED S M, RAY T. Differential evolution with dynamic parameters selection for optimization problems[J]. IEEE Trans.on Evolution Computation, 2014, 18(5): 689-707.

[18] ZHANG L, TANG Y, HUA C, et al. A new particle swarm optimization algorithm with adaptive inertia weight based on Bayesian techniques[J].Applied Soft Computing,2015,28(C): 138-149.

[19] JI W, WANG J, ZHANG J. Improved PSO based on update strategy of double extreme value[J]. International Journal of Control & Automation, 2014, 7(2): 231-240.

[20] TRELEA I. The particle swarm optimization algorithm: convergence analysis and parameter selection[J]. Information Processing Letters, 2003, 85(6): 317-325.

[21] EBERHART R C, SHI Y. Comparing inertia weights and constriction factors in particle swarm optimization[C]∥Proc.of the Congress on Evolutionary Computation, 2000: 84-88.

[22] SHI Y, EBERHART R C. A modified particle swarm optimizer[C]∥Proc.of the IEEE International Conference on Evolutionary Computation, 1998: 69-73.

[23] 朱振虹,夏群利, 蔡春濤, 等. 相控陣導引頭去耦及視線角速率提取算法研究[J]. 戰術導彈技術, 2013, 6(5): 70-75.

ZHU Z H, XIA Q L, CAI C T, et al. Research on phased array seeker decoupling and line of sight rate extraction algorithmic[J]. Tactical Missile Technology, 2013, 6(5): 70-75.