密封式繼電器觸點表面與接觸還原研究*

李文華 周露露

河北工業大學, 天津300130

繼電器觸點的表面形貌對繼電器長期連續工作狀態有直接影響[1]，粗糙表面的幾何結構會影響接觸情況，只有充分了解觸點表面接觸形貌，才能更好地從微觀層面研究觸點接觸過程中的變化。

隨著對粗糙表面研究的不斷深入，傳統的二維評價方法已經不能滿足要求，三維表面形貌的表征可以從不同方面描述粗糙表面，對三維表面的形貌特征分析反而顯得越來越重要。在表面三維形貌的研究中，絕大多數學者利用Weierstrass-Mandelbrot(W-M)函數模擬粗糙表面。文獻[2]使用W-M 函數對粗糙表面輪廓進行擬合，分析了2個接觸粗糙面微凸體個數及其被擠壓高度、接觸面積W-M函數的關系，推導了粗糙面的接觸電阻計算公式，研究了兩粗糙面間的接觸電阻與接觸力的關系。

雖然三維粗糙表面分形方法被越來越多地運用到繼電器接觸表面的研究中，但這些針對的都是單個觸點的表面，對觸點組的分析幾乎沒有。繼電器觸點接觸過程中真實表面的變化很難觀測，通過仿真模擬接觸過程分析得到的參數不具有真實還原性。文獻[3]通過掃描電鏡建立了真實的繼電器觸點接觸表面模型，通過仿真研究了接觸電阻與接觸壓力之間的關系，但該方法尚未研究接觸區域的熱電效應。

因此，本文利用三維非接觸式形貌儀采集三維坐標，計算表面的三維粗糙度參數值和分形維數。掃描觸點表面元素分布，針對特定元素分析觸點的失效機理。從微觀角度分析觸點表面的接觸關系，選定相對觸點平面，提出差平面還原觸點接觸面，為從真實形貌角度進一步建立接觸電阻模型提供了思路。

1 三維形貌分析

1.1 三維粗糙度

本文選取試驗后的一對密封式繼電器觸點為樣本，利用三維非接觸式表面形貌儀掃描得到繼電器動靜觸點的三維表面形貌圖如圖1所示。

選取最小二乘法建立表面形貌模型，通過對多項式函數求偏導，可以得到多項式中相應的未知參數，建立表面形貌的最小二乘中位面，并以此作為三維表面形貌的評定基準面[4]。目前三維形貌參數主要包括4個方面：幅度參數、空間參數、功能參數和綜合參數。本文選取5個代表性的幅度參數進行分析：表面十點高度Sz,表面算術平均偏差Sa，表面均方根偏差Sq，輪廓最大谷深Sv以及輪廓最大峰高Sp[5-6]。

圖1 樣本繼電器觸點

1.2 分形維數

目前，對微觀粗糙表面的表達及接觸分析，主要采用了統計分析和分形理論的方法，分形理論具有尺度無關性，與統計方法相比，可以較好地描述粗糙平面[7]。

二維分形的W-M函數定義式為：

(1)

式中：x為工程表面水平方向的掃描坐標;z(x)為工程表面垂直方向的粗糙輪廓;D為二維分形維數;G為表面特征尺度系數;γ是決定自相似性和頻譜密度的尺度系數；L表示分形輪廓的采樣長度。

Yan等人將滿足分形性質的W-M函數推廣到三維粗糙面，可以更精確地描述粗糙表面形貌[8]。三維分形的W-M函數定義式為：

(2)

式中：D為三維分形維數；G為特征尺度系數，反映z(x)幅值大小，它決定z(x,y)的具體尺寸；M為曲面褶皺的重疊數；m，n為隨機相位，取值范圍為[0,2π]。

分形維數的計算方法有很多種，包括盒維法、差分盒維法、變分法等，其中以盒維法最為常用[9]。本文在非接觸式掃描儀掃描的基礎上，利用MATLAB軟件對圖像的分形維數進行盒維法計算。首先讀取圖1中動靜觸點的真實表面形貌圖，選定相同的觸點面積，利用Bernsen算法對其進行二值化處理。針對轉化后的二值化圖像，用邊長為L1的網格覆蓋整張圖片，數出包含孔和與孔相交的所有網格數N(L1)；再把邊長L1縮小1倍至L2(L2=L1/2)，此時再數出盒子數N(L2)。重復上述步驟，使網格不斷變小，盒子數不斷變多。最后，以lnN(Li)為縱坐標，lnLi為橫坐標作圖，線性回歸處理得到的雙對數坐標圖中的數據點，得到一條直線，則直線斜率的絕對值就是分形維數D。

1.3 三維形貌分析

根據采集的繼電器觸點表面選定區域的三維坐標建立基準面模型，計算得到動靜觸點三維表面粗糙度參數數據如表1所示。

表1 動靜觸點三維表面粗糙度參數數據表

由表1分析可知，繼電器觸頭表面形貌的三維參數Sa與Sq之間滿足以下關系[10]：

Sa=2σ/π≈0.8σ=0.8Sq

(3)

式中，σ是幅度分布的標準偏差，即Sq表面具有大量隨機的、雜亂的尖峰，其表面結構與周期性較強的表面有明顯區別。

Sq對偏離名義高度較大的采樣點比Sa更敏感，而隨機性強的表面中具有大量隨機和局部的信息和結構，使得Sq值總是偏大。對于隨機性較強的表面，Sa/Sq的值都小于0.8；對于規律性較強的表面，Sa/Sq的值基本上略大于0.8。因此，繼電器動觸點表面結構周期性越弱，靜觸點表面結構的周期性越強。

分析繼電器動、靜觸頭的最大峰高和最大谷深之和，用V表示：

V=Sp+Sv

(4)

由表可知，繼電器動觸點V值絕對值比靜觸點的V值絕對值大很多，表明動觸點的起伏變化明顯，幅度較大，而靜觸點的幅度變化較小，相對平坦。繼電器動靜觸點表面的粗糙度參數滿足以下關系：

(5)

根據三維非接觸式形貌掃描儀掃描得到的動靜觸點的形貌圖，按照盒維法計算得到動靜觸點的二維分形維數和三維分形維數如表2所示。

表2 觸點組分形維數表

分形維數D與表面微觀形貌的幅值變化的劇烈程度有關，D值大表明微觀細節豐富；D值越小表明低頻成分越多[10]。一般來說，三維分形維數值比二維分形維數值大1；且Sa值小時，D值則較大。這是因為Sa小時，表面的微觀結構精細，短波長成分較多，因此D值較大。從三維形貌角度來說，二維或三維粗糙度參數越大，繼電器觸點的失效越表現為凹凸明顯的微動磨損失效形式；反之，觸點的失效表現為顆粒沉積形式。

2 表面成分分析

2.1 SEM分析

繼電器內部只有塑料導線、線圈骨架、磁鐵和塑料底盤等基本元件，觸點材料為金。這些物質在加速壽命試驗的運動過程中可能會分解出碳氫化合物。觸點接觸時出現的機械摩擦會形成高分子量的無定型固體粒子，隨著運動次數的增多，固體粒子不斷堆積，破壞觸點表面膜，使觸點絕緣。

為了更好地觀察動靜觸點在運動過程中表面形貌的變化，本文利用掃描電鏡進行觸點表面掃描，圖2(a)和(b)分別是繼電器動、靜觸點表面的SEM圖。

圖2 動靜觸點表面SEM圖

2個觸點的表面狀態是材料轉移的直觀表現。直流作用下的材料轉移分為細轉移和粗轉移2種形式，“細轉移”在陰極表面形成尖峰，在陽極表面上有狹窄的陷坑。“粗轉移”的外形更多是平面狀的。試驗中動觸點與電源正極連接，表現為陽極現象。動觸點表面凹凸不平，燒蝕現象比較明顯。靜觸點表面平整，噴濺沉積的微粒大小相對均勻，出現小麻點狀，局部有燒蝕出現。觸點表面材料從陽極轉移到陰極，即從動觸點向靜觸點轉移。

為更好地研究繼電器的失效機理，分析表3所示動、靜觸點表面元素含量。

表3 動、靜觸點表面元素含量

由表3可知，不管是動觸點還是靜觸點，Au，C，N，O的含量很高，S，Ag等元素都較少，其中C，N和部分O均為污染引入。樣本所用觸點材料為Au，Au是性能相當穩定的金屬材料，一般作為鍍層材料鍍在非貴金屬表面。Au鍍層較薄時，鍍層表面會出現微孔，在長期使用時形成微孔腐蝕，破壞了原來良好的電接觸性能，如圖2(a)所示。

2.2 特定元素分析

由表3可知，Au和C的含量很高，利用The SIMS Mapper軟件分析這2種特定元素的分布。將樣品安裝在大小為6mm標準SIMS樣品架中，確保觸點接觸的上表面位于分析平面。以MCs +簇的形式收集負二次離子的同時使用5keV Cs +一次離子對觸點表面元素進行分析。在保證不影響觸點表面損傷的前提下，根據測試深度的不同使成像電流從1nA～50nA變化。選定觸點表面分析區域的面積為4mm×4mm，圖3顯示了動靜觸點表面Au和C 元素的分布圖，右側圖像為2種元素的3D分布圖，表面下方的柱體沒有參與分析；左側圖像為假設C和Au 2種元素在整個接觸表面含量為100%，根據近似的濃度校準含量，縱坐標為原始計數率相對數據；左下方圖顯示了選定的凹坑深度為800μm處2種元素的相對數據。

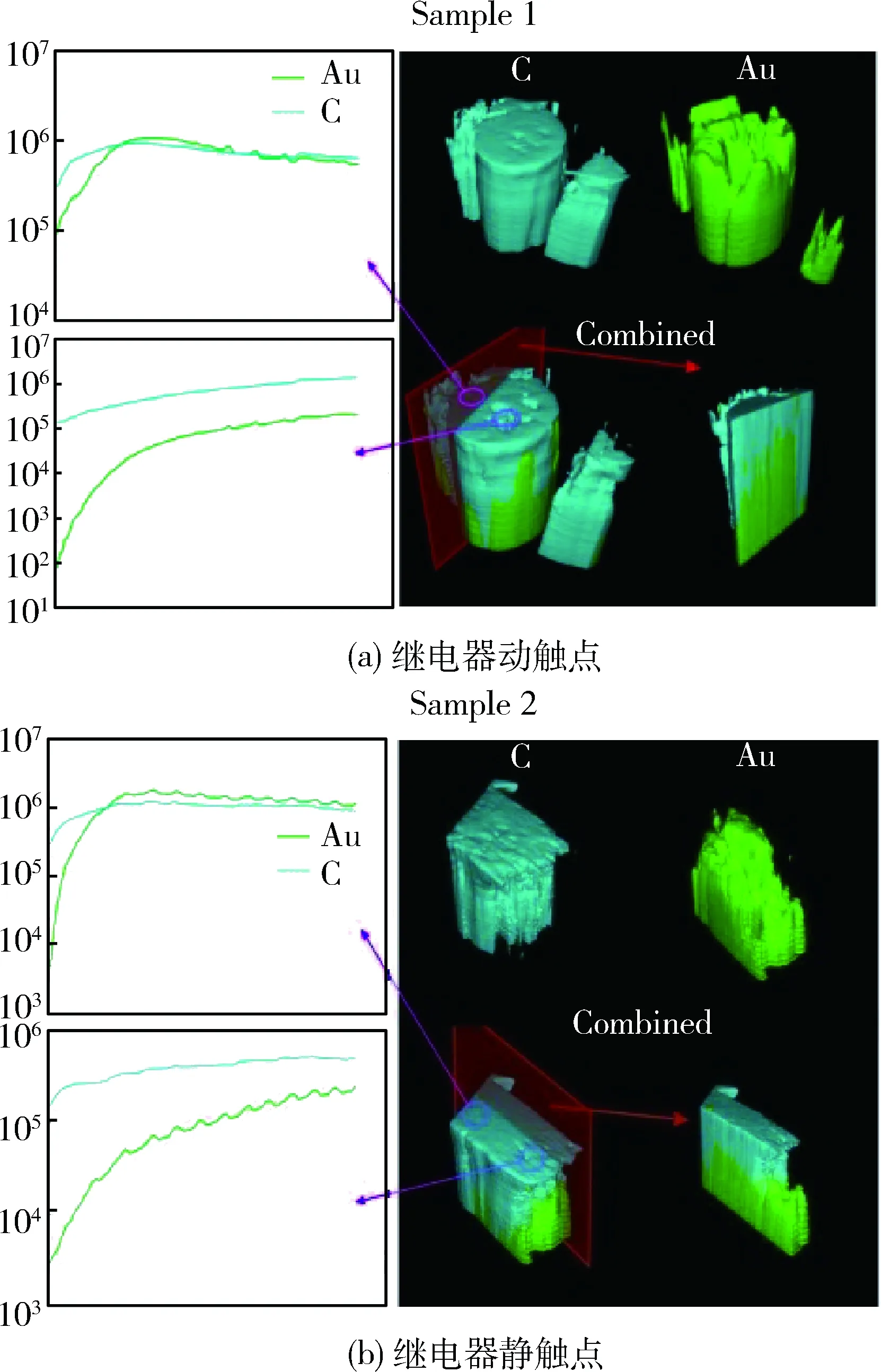
圖3 動靜觸點表面特定元素分布圖

由圖3可知，動、靜觸點相對平坦區域的Au和C原始計數率相對數據相當，而凹坑處的C含量明顯大于Au含量，這說明Au在微動過程中容易被磨損，燒蝕處容易粘著碳顆粒。

2.3 微量元素分析

雖然是密封式繼電器，但是在生產前期過程中可能會引入若干微量污染物質，在繼電器工作過程中會析出有害成分，這些會造成觸點表面成分的變化。在觸點周圍介質中以蒸汽狀態存在的有機物質吸附在觸點表面，并在化學吸附作用下形成有機層。

觸點在制造過程中，經高溫成型，觸點表面部分污染C與基底材料發生化學反應，生成穩定的碳化物，沉積在觸點表面。在觸點的不斷吸合過程中，伴隨有電弧現象，電弧會將部分沉積物燒為碳，碳化物在觸點閉合過程中也會引燃電弧，循環往復，繞線塑料和底盤塑料分解得到的碳氫化合物便會吸附在觸點表面。表面膜上的C和O成分形成可以用一下化學式解釋：

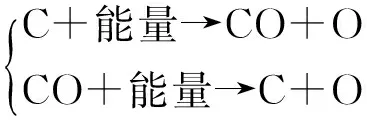
(6)

動觸點表面元素含少量P，P的來源可能和松香/焊料有關。氧化物、硫化物等非有機污染主要是金屬觸點與部分氣體化學反應的產物，也包括水和制造過程中的某些金屬蒸汽沉積，這些物質大部分導電性都很差，有的還會形成不易破壞的暗膜，或形成微小溶池，加劇觸點侵蝕，使接觸電阻增大。在長期貯存的繼電器密封性出現問題時，大氣里的水汽、腐蝕性氣體等通過鍍層的微裂紋、小孔，利用微管毛細作用滲入并接觸到基體金屬并沉積下來后，接觸表面會形成電解液。當Au和極少的Ag之間可以形成原電池，觸點表面發生氧化還原反應，形成氧化物或者硫化物的堆積：

(7)

3 觸點組接觸面還原

3.1 接觸電阻模型

接觸電阻的計算一直以來都是電接觸研究的一個重要課題。R.Holm最早建立了Holm接觸電阻模型，之后也有學者在Holm基礎上提出了考慮多斑點、表面膜、溫度等因素的更加符合實際接觸情況的接觸電阻模型，但是這些接觸電阻計算公式很難直接應用到實際工程設計中。

對于觸點這類粗糙表面而言，實際接觸面積取決于負載的大小和2個接觸表面的表面形貌。2個粗糙表面實際接觸的并不是整個接觸表面，而是一些微凸體之間的接觸，從而形成離散的接觸點或微小的接觸面，這些接觸點和接觸面就構成了實際接觸面積。要得到粗糙接觸面的實際接觸面積，還需要根據實際接觸時的表面形貌分析得到接觸斑點的個數和半徑才能針對觸點進行定量計算。

樣本繼電器觸點接觸時的三維幾何模型如圖4(a)所示。不管是哪種材料導體的接觸，接觸面之間都存在接觸表面的不連續性，但是粗糙表面的微凸體的變形存在連續性。兩個粗糙表面的接觸可以用一個等同粗糙表面和一個剛性光滑表面接觸來代替[11]。簡化動靜觸點表面的接觸變形關系如圖4(b)所示，其真正的接觸區域是在微凸體相對較高的頂部區域。

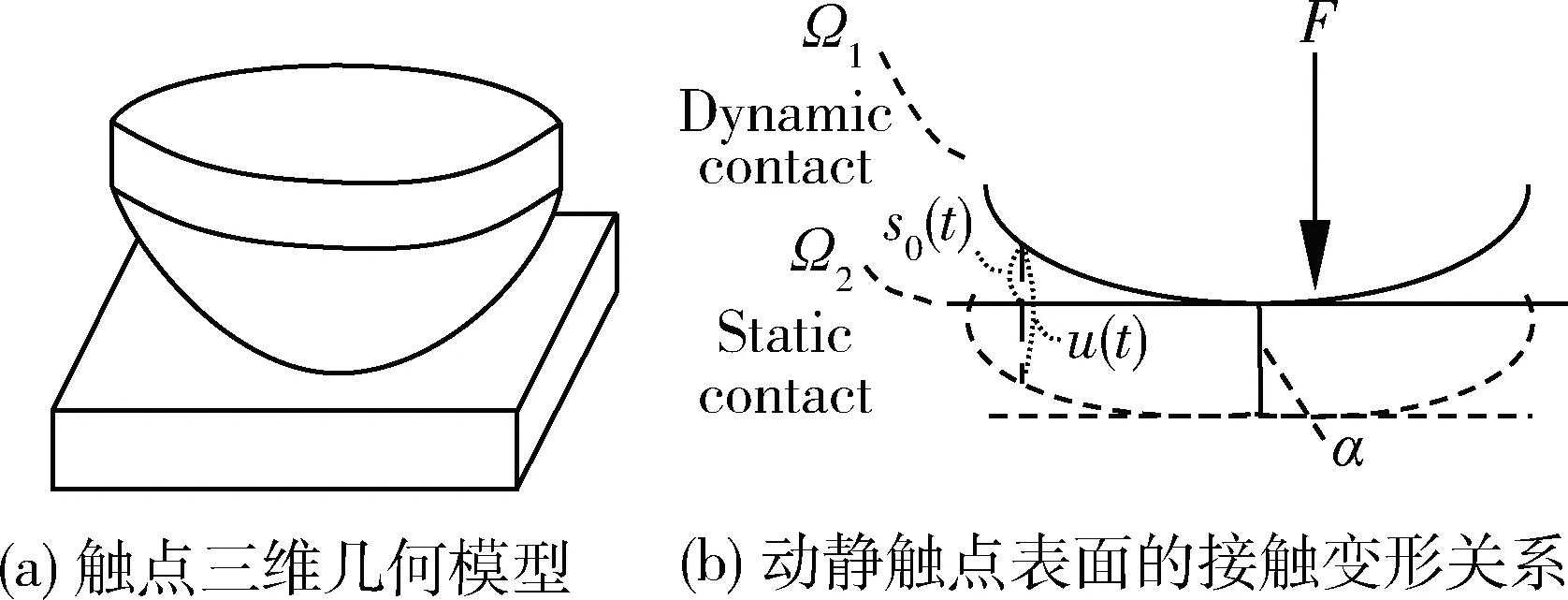
圖4 觸點三維模型及假設模型

本文基于粗糙表面微凸體變形的連續性和光滑性原理，尋找應力和形變關系。當2個接觸面Ω1和Ω2在力F的作用下發生接觸時，存在如下關系[3]：

(8)

式中，u(x)是2個物體接觸表面的變形位移，即形變量；s0(x)是2個物體的初始間隙，它們都是空間坐標x的函數；α是接觸體中心的剛體平動位移。

3.2 觸點組表面形貌還原

三維非接觸式掃描儀按照線掃描方式掃描觸點表面建立基準面，在同一基準面的基礎上記錄觸點表面的高度，掃描得到的數據量足以完全反應繼電器觸點表面形貌。本文利用三維非接觸式掃描儀掃描時，動觸點和靜觸點所處的方位一致，在此基礎上用MATLAB還原出的觸點真實表面形貌都是接觸面方向向上的圖形。

考慮到觸點在動作過程中是接觸狀態，當兩金屬表面互相接觸時，最高的粗糙峰頂最先接觸。通常會出現較大的局部應力，使接觸點產生很強的壓縮作用，并使新的粗糙峰頂參與接觸，承受大部分荷載。當接觸的粗糙峰頂數增加足以承受所施加的荷載時，接觸過程才最終完成。在此基礎上，本文假設觸點的2個接觸表面為彈性表面，提出用動靜觸點表面差平面作為建立接觸電阻模型的基礎。

為了更好地模擬動靜觸點的接觸過程，按照圖1選定觸點對應的接觸區域，保證選定區域的矩陣大小相同，還原動靜觸點的三維形貌如圖5所示。

先根據繼電器觸點接觸的位置調整好動靜觸點的接觸面，以動觸點為相對參考平面，將靜觸點進行鏡像對稱。MATLAB讀取圖5(b)所示粗糙平面的三維坐標，利用鏡像變換矩陣對表面進行鏡像對稱：

(9)

其中，a,b,c為鏡像線ax+by+c=0的系數。

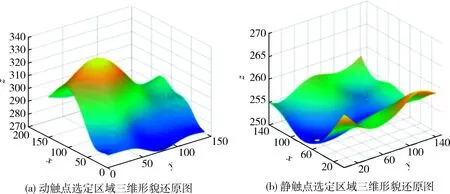
圖5 觸點選定區域三維形貌還原圖

得到圖5(b)的鏡像圖后，計算動觸點和靜觸點鏡像圖后對應高度之和，以動靜觸點表面高度和的最高值所在的平面作為基準面，計算對應的高度和與最高點的差值，得到一個差平面。這個差平面就是之后建立一定負載、一定壓力下觸點接觸電阻模型的前提。得到的動靜觸點組粗糙表面差平面如圖6所示。

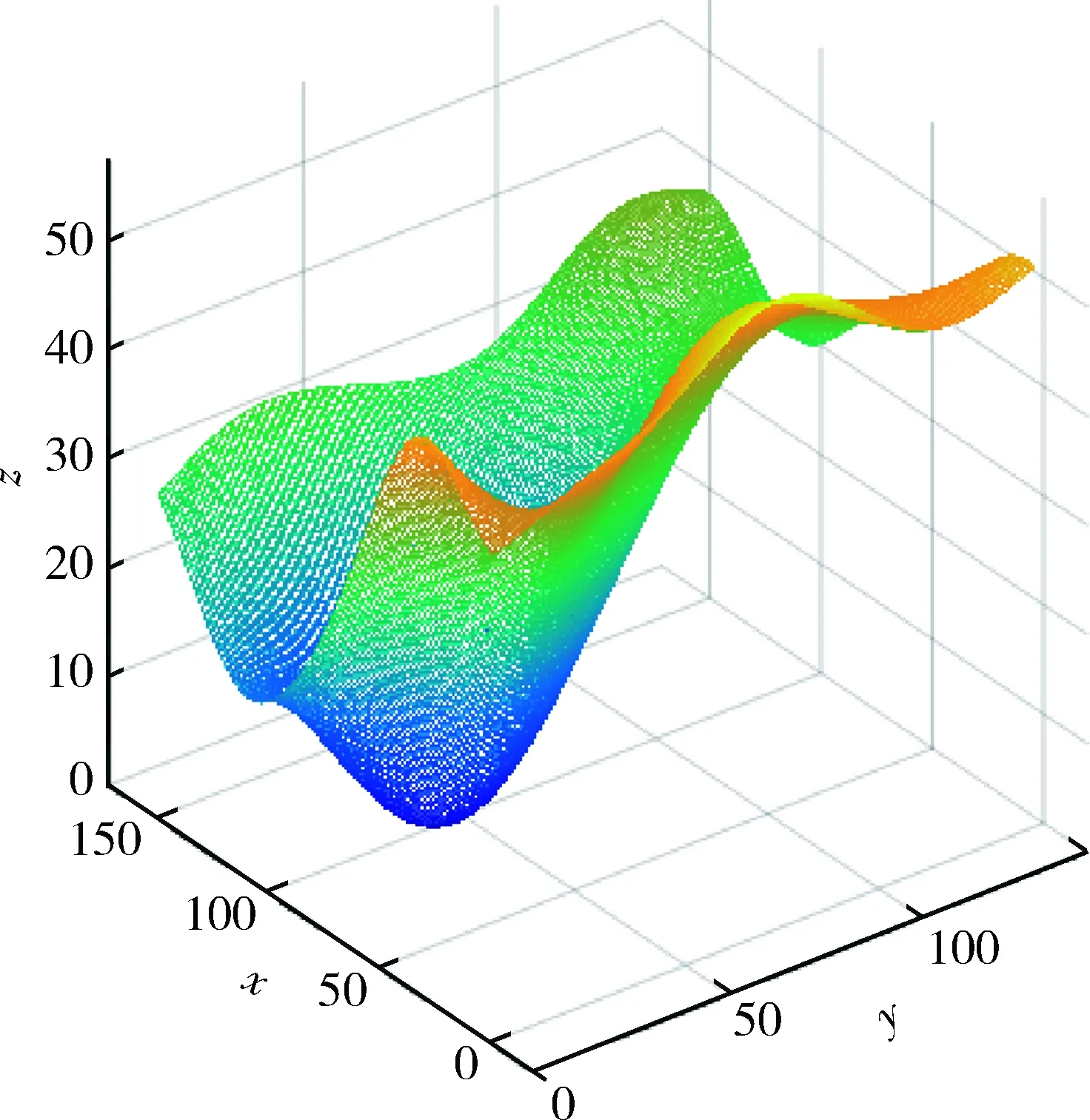
圖6 觸點組粗糙表面差平面圖

圖6反映了繼電器觸點組在接觸過程中的表面形貌狀況，通過試驗可以分析出繼電器觸點在運動過程總的負載大小以及觸點組之間的壓力大小，壓力與接觸表面的形變量息息相關。建立形變量和差平面的對應模型，可以得到觸點接觸時的實際接觸面積，由此建立觸點接觸電阻模型。

4 結論

對觸點表面進行了形貌和失效分析，提出差平面概念還原觸點接觸面，從三維表面差平面研究動靜觸點真實的接觸狀況，打破用仿真軟件仿真模擬接觸過程的局限性，對從微觀層面建立觸點接觸電阻模型進一步研究具有一定的指導作用。

后期將著重研究通過試驗分析繼電器觸點在運動過程中總的負載大小以及觸點組之間的壓力大小，建立形變量和差平面的對應模型，從而得到觸點接觸時的實際接觸面積以及接觸電阻模型。

[1] 徐富春,王水菊,湯丁亮,張棋河,林秀華,陸寧懿. 電磁繼電器觸點表面的SEM和XPS研究[J]. 廈門大學學報(自然科學版),2001,40(4):857-861.(Xu Fuchun, Wang Shuiju, Tang Dingliang, Zhang Qihe, Lin Xiuhua, Lu Ningyi. Studies on Contact Points Wear of Electromagnetic Relay by SEM and XPS[J].Journal of Xiamen University (Natural Science), 2001, 40(4): 857-861.)

[2] 汪久根,馮蘭蘭,李陽. 粗糙表面形貌對電蝕的影響[J]. 浙江大學學報(工學版),2015,49(11):2025-2032.(Wang Jiugen, Feng Lanlan, Li Yang. Influences of Surface Topography on Electrical Pitting[J].Journal of Zhejiang University (Engineering Science), 2015, 49(11): 2025-2032.)

[3] Liu H, Leray D, Colin S, et al. Finite Element Based Surface Roughness Study for Ohmic Contact of Microswitches[C]. 2012 IEEE 58th Holm Conference on Electrical Contacts (Holm). IEEE, 2012: 1-10.

[4] 炊明偉,馮有前,王崴,李正朝,徐曉東. 改進中值濾波和最小二乘法在三維表面評定中的應用[J]. 表面技術,2012,41(6):118-121.(Chui Mingwei, Feng Youqian, Wang Wei, Li Zhengchao, Xu Xiaodong. The Application of the Improved Median Filter and Least Square Method in Evaluation of 3D Surface Topography[J]. Surface Technology, 2012, 41(6): 118-121.)

[5] Liao Y, Stephenson D A, Ni J. Multiple-Scale Wavelet Decomposition, 3D Surface Feature Exaction and Applications[J].Journal of Manufacturing Science and Engineering, 2012, 134(1): 011005.

[6] 李小兵,王清華.基于多尺度理論的三維表面形貌表征研究[J]. 機械設計與研究, 2014, 30(2): 119-120.(Li Xiaobing, Wang Qinghua. Research of Multi-scale Theory in the 3-D Surface Morphology Characterization[J].Machine Design and Research, 2014, 30(2): 119-120.)

[7] 張程賓,陳永平,施明恒,付盼盼,吳嘉峰. 表面粗糙度的分形特征及其對微通道內層流流動的影響[J]. 物理學報,2009,58(10):7050-7056.(Zhang Chengbin, Chen Yongping, Shi Mingheng, Fu Panpan, Wu Jiafeng. Fractal Characteristics of Surface Roughness and Its Effect on Laminar Flow in Microchannels[J].Acta Physica Sinica, 2009,58(10): 7050-7056.)

[8] Yan W, Komvopoilos K. Contact Analysis of Elastic-plastic Fractal Surfaces[J].Journal of Applied Physics,1998,84(7):3617-3624.

[9] 朱紀磊,湯慧萍,奚正平,邸小波. 多孔結構分形分析及其在材料性能預報中的應用[J]. 稀有金屬材料與工程,2009,38(12):2106-2110.(Zhu Jilei, Tang Huiping, Xi Zhengping, Di Xiaobo.Fractal Analysis of Pore Structure and Its Application for Prediction of Permeability and Porosity[J]. Rare Metal Materials and Engineering, 2009,38(12): 2106-2110.)

[10] 李成貴,張國雄,袁長良. 分形維數與表面粗糙度參數的關系[J]. 工具技術,1997,31(12):36-38.(Li Chenggui, Zhang Guoxiong, Yuan Changliang. The Relationship Between the Fractal Dimension and Surface Roughness Parameters[J]. Tool Technology, 1997,31(12): 36-38.)

[11] 趙永武,呂彥明,蔣建忠. 新的粗糙表面彈塑性接觸模型[J]. 機械工程學報,2007,43(3):95-101.(Zhao Yongwu, Lv Yanming, Jiang Jianzhong. New Elastic-plastic Model for the Contact of Rough Surfaces[J]. Chinese Journal of Mechanical Engineering, 2007, 43(3):95-101.