聯合攻角約束視場角和落角的末制導律設計
曾耀華 谷永艷 李 娟
四川航天系統工程研究所,成都 610100
傳統的比例導引律結構形式簡單、需測量少、彈道特性好且制導精度高,在工程上得到了廣泛應用。為了更好地發揮精確制導武器(如反坦克導彈)摧毀目標效能,要求能以期望的落角較小的攻角擊中目標,而采用傳統的比例導引律末端落角基本上已由初始制導視線角大小決定,不能主動控制落角使得傳統比例導引律在該類武器中越來越難以適應。因此,出現了最早由Kim研究的偏置比例導引律(BPNG)[1],通過在傳統比例導引律基礎上加上一個與落角偏差有關的偏置項構成。此后,隨著越來越多的武器要求具有規定落角進行攻擊,又出現了多種不同形式的帶落角約束導引律[2-3],其中比較典型的一類變系數比例導引律如文獻[4]中描述,其形式類似BPNG,可看作是變系數的BPNG,其不需估計剩余時間而能達到期望落角約束。但該方法有適用局限,驗證表明很多情況下難以達到需要的高制導精度。其他比較好的導引律如滑模導引律[5-6],通過引入滑模變結構控制,提高落角約束項對測量或估計誤差的魯棒性。在帶有偏置項的比例導引律中,由于偏置項的存在,可能會出現過大的視場角導致導引頭丟失跟蹤目標,因此還需要對視場角進行約束。文獻[7]提出了一種開關邏輯型視場角約束方法,當視場角達到約束閾值時加入一個與視場角有關的約束偏置項,否則撤銷該約束偏置項,通過設置合適的系數,可以平穩調節偏置項大小、平穩約束視場角在規定范圍內。
任何的導引律其制導精度必須優先保證,由于傳統的比例導引律具有高制導精度,因此文中以傳統比例導引律為基礎,借鑒偏置比例導引(BPNG)思想,基于滑模變結構控制的強魯棒性,分析可見帶落角約束的滑模導引律總體上為類偏置比例導引律形式,故設計了以比例導引為基本項,加上其他約束偏置項的結構構型為主要形式的末制導律。該末制導律在帶重力補償的傳統比例導引律基礎上,加入基于變參數滑模調節項和視線偏差比例項組成的落角約束變結構偏置項。同時,為約束導引頭視場角超限,使該偏置項乘上一個指數形式的視場角約束帶通型系數;為約束攻角過大,根據氣動參數計算允許極限攻角對應的極限過載,把偏置項值限制在該極限過載內。最后,與最優系數BPNG方法通過對比仿真進行了驗證。
1 多約束末制導律
1.1 落角約束末制導律
按照質點運動假設,建立俯仰平面內的彈目相對運動關系如圖1所示。圖中,M為導彈,T為目標,MT距離為彈目距r,MT連線為視線,視線傾角為q;導彈運動參數主要考慮彈道傾角θm、速度vm、速度相對視線的偏離角ηm=q-θm以及改變速度矢量方向的法向加速度控制量ac;目標運動參數主要考慮速度傾角θt、速度vt和速度相對視線的偏離角ηt=q-θt。
圖1 彈目相對運動關系
建立彈目相對運動方程:
(1)
基于以上關系,根據零化彈-目視線角速率的準平行接近原理[4],給定終點時刻tf的期望導彈終點彈道傾角θm(tf),預測預估目標終點速度傾角θt(tf),對于地面目標,一般可認為θt(tf)≈0。按照下式計算期望視線傾角λD為:
(2)
根據偏置比例導引原理[1],參考滑模變結構制導律思想[5-6],考慮重力補償,本文提出帶落角約束的末制導律形式如下:
(3)
式中,第1項為傳統的比例導引,第2項為偏置項,第3項為滑模變結構項,最后一項為重力補償項;N為導航比,kq和kg均為正的系數。
重寫式(3),表示為以下2項之和:
(4)
其中,aycsv為考慮重力補償的傳統比例導引項;aycsb為考慮落角約束的變結構偏置項,其由2部分組成:與視線偏差變化率有關的比例項和滑模調節項。
定義落角偏差變化率表示為:
(5)
其中,剩余時間采用如下估算公式[8]:
(6)
滑模項的存在,能夠弱化剩余時間估計不準導致的大脫靶量。選取的滑模面切換函數為:
(7)
式中,k1>0,k2>0。
選取的滑模趨近律為:
(8)
式中,k>0,μ>0。
飽和函數形式為:
sat(S,δ)=S/|S|+δ
(9)
式中,飽和因子δ>0,δ越大,趨近飽和越平緩。
對滑模趨近調節系數ε設計為自適應變參數形式,其取值為與視線角速度有關的量,在末端能夠保證獲得最佳的脫靶量和較小的攻角,如下:
(10)
式中,系數ks>0。
1.2 落角偏差變化率約束
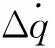
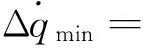
(11)
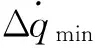
Ay1(·)函數表達為彈體系下的攻角對應的有舵偏時的法向加速度值,根據導彈動力學模型,給定時刻t導彈在某一攻角下所受的垂直彈軸的法向加速度可用下式近似計算:
(12)
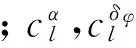
(13)
然后乘以指數形式系數進行平滑過渡:
(14)
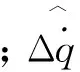
1.3 聯合攻角和視場角約束
根據比例導引原理,傳統比例導引項aycsv具有零化視線角速度的作用效果,即隨著導引制導控制的不斷進行,彈目視線角速度具有趨于0的平衡態,同時使得導彈速度矢量指向趨向視線方向。相反,落角約束變結構偏置項aycsb具有破壞aycsv零化視線角速度的反作用,使得導彈速度矢量指向偏離視線方向。速度矢量指向趨向視線方向的同時也具有使彈軸指向趨向視線方向的效果,而速度矢量指向偏離視線方向的同時也使得彈軸指向偏離視線方向。彈軸指向偏離視線方向導致導引頭框架角增大,因此,為防止導引頭框架運動范圍超限導致無法跟蹤
目標,要求控制導引頭框架角大小,約束彈軸指向嚴重偏離視線,即視場角約束。
對于具有偏航和俯仰運動的兩軸伺服平臺式導引頭,根據導引頭性能指標,給定導引頭俯仰框架角極限范圍:qb∈[qbmin,qbmax]。無論對于BTT還是STT控制方式,aycsb的存在,主要影響俯仰框架方向,因此,只考慮俯仰框架角的約束。本文采用改進的框架角約束方式[7],約束項作為系數用于調整aycsb的值,即aycsb乘以視場角約束帶通型系數。該系數采用指數形式表示為:
kqb=(1-e-57.3τq(qb-qbmin))(1-e-57.3τq(qbmax-qb))
(15)
式中,τq為正的時間常數;kqb為約束項系數,且若kqb<0,則令kqb=0。
根據文獻[7]的思想,可以設定一個閾值作為約束項系數起作用的緩沖區,即若滿足
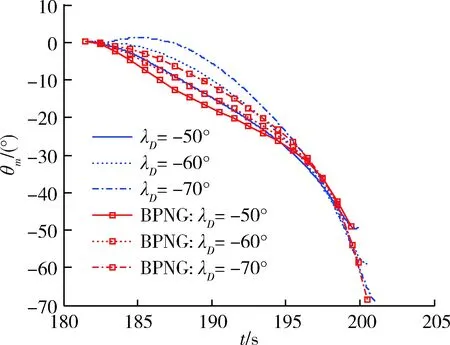
qbmin+Δη (16) 則令kqb=1,其中Δη為正的框架角緩沖區寬度。 最后,根據允許極限攻角要求,對aycsb進行攻角約束。要求約束滿足如下不等式 (17) 即 (18) 其中, (19) 式中,舵偏上標“1”表示上一周期的值。 (20) 以某小型攻擊巡飛彈末制導攻擊目標為例,應用本文設計的多約束末制導律進行數學仿真分析,同時使用偏置比例導引律(BPNG)進行對比仿真,其形式如下: (21) 該巡飛彈以平飛巡航方式進行偵察,發現待攻擊目標后,導引頭鎖定目標,巡飛彈轉入大落角導引攻擊末制導。巡飛彈鎖定目標時速度為30m/s,飛行高度為300m,鎖定目標時刻彈目距離800m。設置參數N=3,kq=2,ks=3,要求飛行攻角范圍α∈[-6°,12°],導引頭俯仰框架角范圍qb∈[-30°,16°],緩沖區寬度Δη=3。 不考慮彈目距離估計偏差進行仿真,即Δr=0,2種導引方法仿真結果比對見表1,從表中可見2種方法落角與期望值的偏差、脫靶量基本相當,但本文方法的落點攻角比BPNG的小。圖2~4為相應仿真曲線,其中從圖4可見,受視場角約束的作用,本文方法λD=-70°的仿真曲線表明俯仰框架角受到約束不至于超限。 表1 無彈目距離估計偏差仿真落點比對結果 圖2 彈道傾角變化曲線 圖3 攻角變化曲線 圖4 俯仰框架角變化曲線 為檢驗彈目距離估計偏差對2種方法制導誤差的影響,人為加入固定的正負彈目距離估計偏差進行仿真,即Δr=±100m,比對統計結果見表2,從表中數據可見,本文方法落角與期望值的偏差明顯比BPNG小,正偏差時2種方法脫靶量基本相當,但當負偏差、大落角(-70°)時BPNG脫靶量出現超1.3m。可見,本文方法對彈目距離估計偏差有更強的魯棒性。 表2 有彈目距離估計偏差仿真落點比對結果 以要求對落角進行控制的目標攻擊末制導律為核心設計對象,在帶重力補償的傳統比例導引律基礎上,設計了基于變參數滑模調節項和視線偏差比例項組成的落角約束變結構偏置項,構成了比例導引加偏置項形式的末制導律。滑模調節項采用變參數的滑模飽和函數,調節視線角速度和視線偏差占比分配,以達到既約束落角又保證制導精度。視線偏差比例項為視線偏差對剩余時間變化率成比例的乘積項,直接控制視線偏差趨向0。同時,考慮到偏置項可能導致導引頭視場角超限和飛行攻角過大,設計了指數形式的視場角約束帶通型系數,通過該系數乘上偏置項達到視場角約束的目的,合理調節系數時間常數以穩定控制,且可通過設置緩沖區來限制該系數起作用的范圍。另外,根據氣動參數計算允許極限攻角對應的極限過載,并把偏置項值限制在該極限過載內達到約束攻角的目的。通過對比仿真,驗證了本文所提末制導律的有效性和魯棒性,結果表明本文方法具有更小的落角偏差和末端攻角又不失高制導精度,對剩余時間估計誤差容忍性更好,同時保證視場角不超限,有利于導引頭持續跟蹤目標。本文所設計的末制導律結構形式簡單,需測量少,對估計誤差不敏感,工程可實現。 [1] Kim B S, Lee J G, Han H S. Biased PNG Law for Impact with Angular Constraint[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(1): 277-288. [2] 張寬橋, 楊鎖昌, 張凱. 帶落角約束的導引律研究進展[J]. 飛航導彈, 2016, (7): 77-82. (Zhang Kuangqiao, Yang Suochang, Zhang Kai. Research Advances of Proportional Navigation Law with Impact Angle Constraint [J]. Aerodyn-amic Missile Journal, 2016, (7): 77-82.) [3] 趙曜, 廖選平, 遲學謙, 等. 終端約束末制導律綜述[J]. 航天控制, 2017, 35(2): 89-98. (Zhao Yao, Liao Xuanping, Chi Xueqian, et al. A Survey of Terminal Constrained Guidance Law [J]. Aerospace Control, 2017, 35(2): 89-98.) [4] 覃天, 陳萬春, 邢曉嵐. 一種帶落角約束的精確導引方法(英文)[J]. 宇航學報, 2012, 33(5): 570-576. (Tan Tian, Chen Wanchun, Xing Xiaolan. A Method for Precision Missile Guidance with Impact Attitude Angle Constraint [J]. Journal of Astronautics, 2012, 33(5): 570-576.) [5] 張寬橋, 楊鎖昌, 王剛. 帶落角約束的有限時間收斂末制導律研究[J]. 彈道學報, 2015, 27(4): 30-36. (Zhang Kuanqiao, Yang Suochang, Wang Gang. Research of Finite-time Convergence Terminal Guidance Law with Impact Angle Constraint [J]. Journal of Ballistics, 2015, 27(4): 30-36.) [6] 辛騰達, 范慧林, 王靖華, 等. 帶落角約束的空地導彈滑模末制導律研究[J], 現代防御技術, 2016, 44(2): 86-91. (Xin Tengda, Fan Huiling, Wang Jinghua, et al. Sliding Mode Terminal Guidance Law for Air to Ground Missile with Impact Angle Constraint [J]. Modern Defence Technology, 2016, 44(2): 86-91.) [7] 顧家立, 陳萬春. 一種帶導引頭視角和落角約束的導引方法[J]. 宇航學報, 2013, 34(6): 782-787. (Gu Jiali, Chen Wanchun. Homing Guidance with Look Angle and Impact Angle Constraints [J]. Journal of Astronautics, 2013, 34(6): 782-787.) [8] 張春妍, 宋建梅, 侯博, 等. 帶落角和時間約束的網絡化導彈協同制導律[J]. 兵工學報, 2016, 37(3): 431-438. (Zhang Chunyan, Song Jianmei, Hou Bo, et al. Cooperative Guidance Law with Impact Angle and Impact Time Constraints for Networked Missiles [J]. Acta Armamentarii, 2016, 37(3): 431-438.)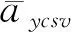
2 仿真分析
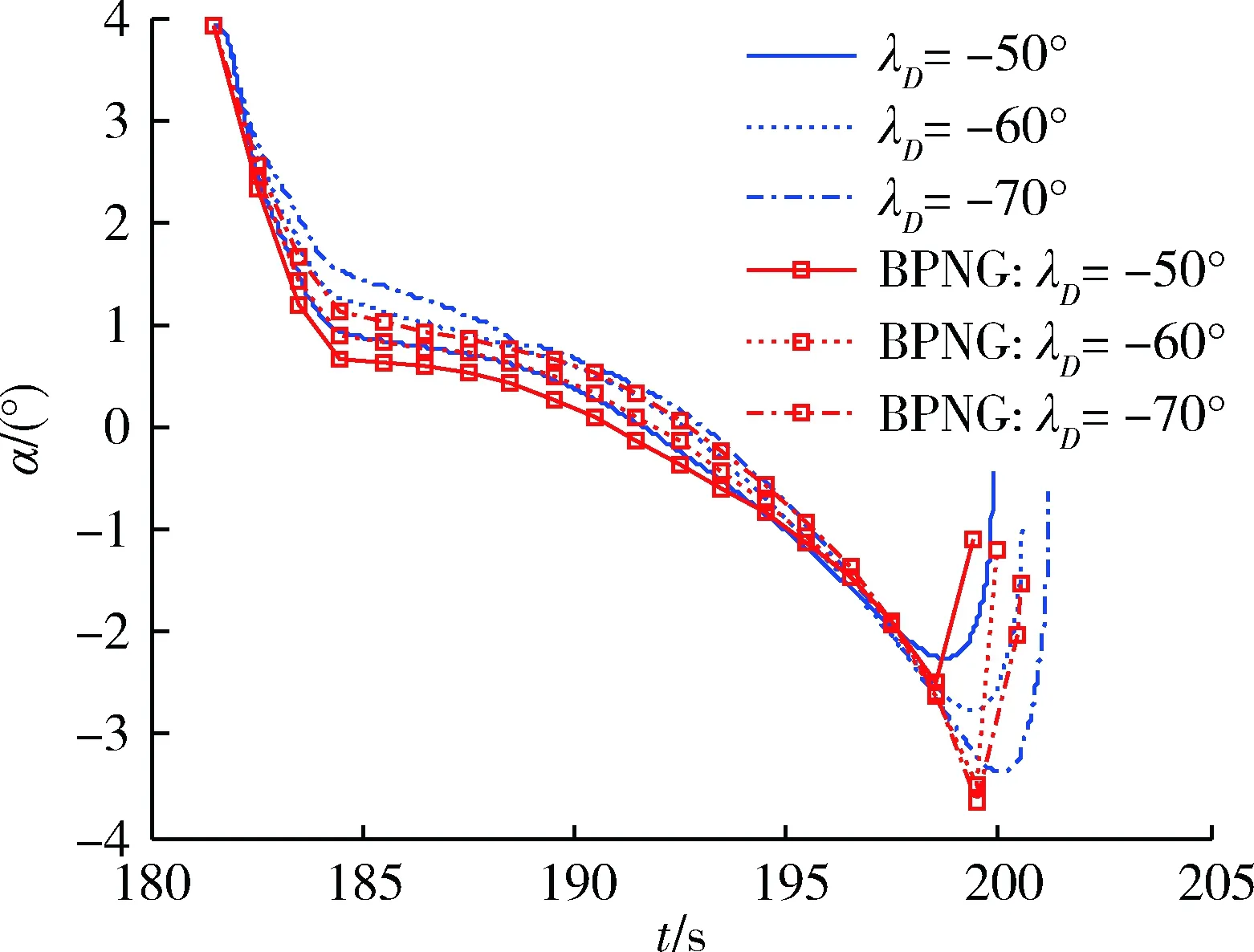
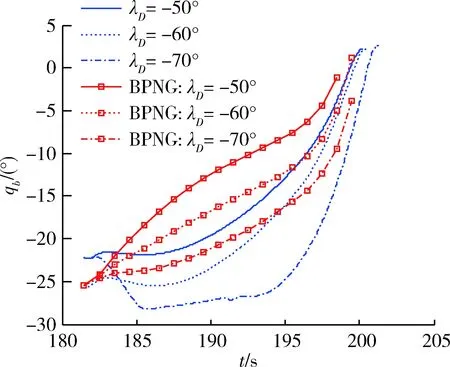
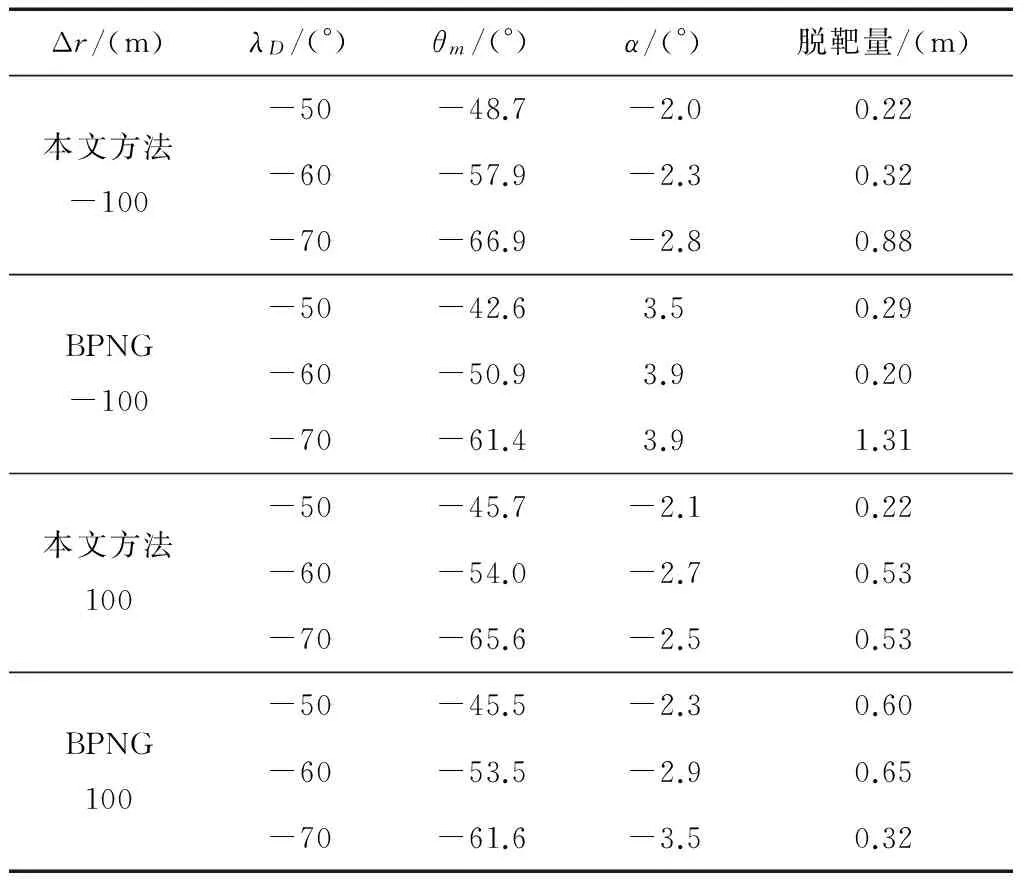
3 結論

