基于指數曲線的運載火箭推力調節電機速度控制方法

孫海峰 胡海峰 宋征宇

北京航天自動控制研究所，北京100854

運載火箭推力調節電機是一種兩相混合式步進電機。在步進電機控制中，好的電機加減速速度曲線能保證在啟動和升速時步進電機產生足夠的轉矩驅動負載，達到規定的速度和加速度，加降速時負載不產生失步或過沖，能停止在規劃的位置。設計一個好的加減速控制曲線對規劃電機實時快速、準確平穩運動，充分發揮步進電機優勢起到了重要作用[1]。

本文從推力調節步進電機的矩頻特性和步頻特性出發，根據轉矩隨頻率的變化規律推導出來一種基于指數曲線的推力調節電機速度的控制方法。基于指數曲線的速度控制方法符合步進電機加減速過程的運動規律，能充分利用步進電機的有效轉矩，快速響應性能好，升降時間短，從而實現步進電機的平穩控制，避免啟動和停止過程的失步或過程，滿足飛行控制對調節角度較高的精度要求。

1 步進電機運行特性[2-3]

要實現步進電機的快速準確定位就要保證電機在不失步和過沖的情況下起停，并以最快的速度運行到指定位置，然而由步進電機典型的矩頻特性曲線(圖1)可以看出，電機的轉矩并非恒定不變，在驅動脈沖頻率較低時，輸出轉矩較大，當驅動脈沖頻率上升時，輸出轉矩會降低。推力調節步進電機的控制率設計就是尋求一種與電機矩頻特性相適應的速度控制方案。

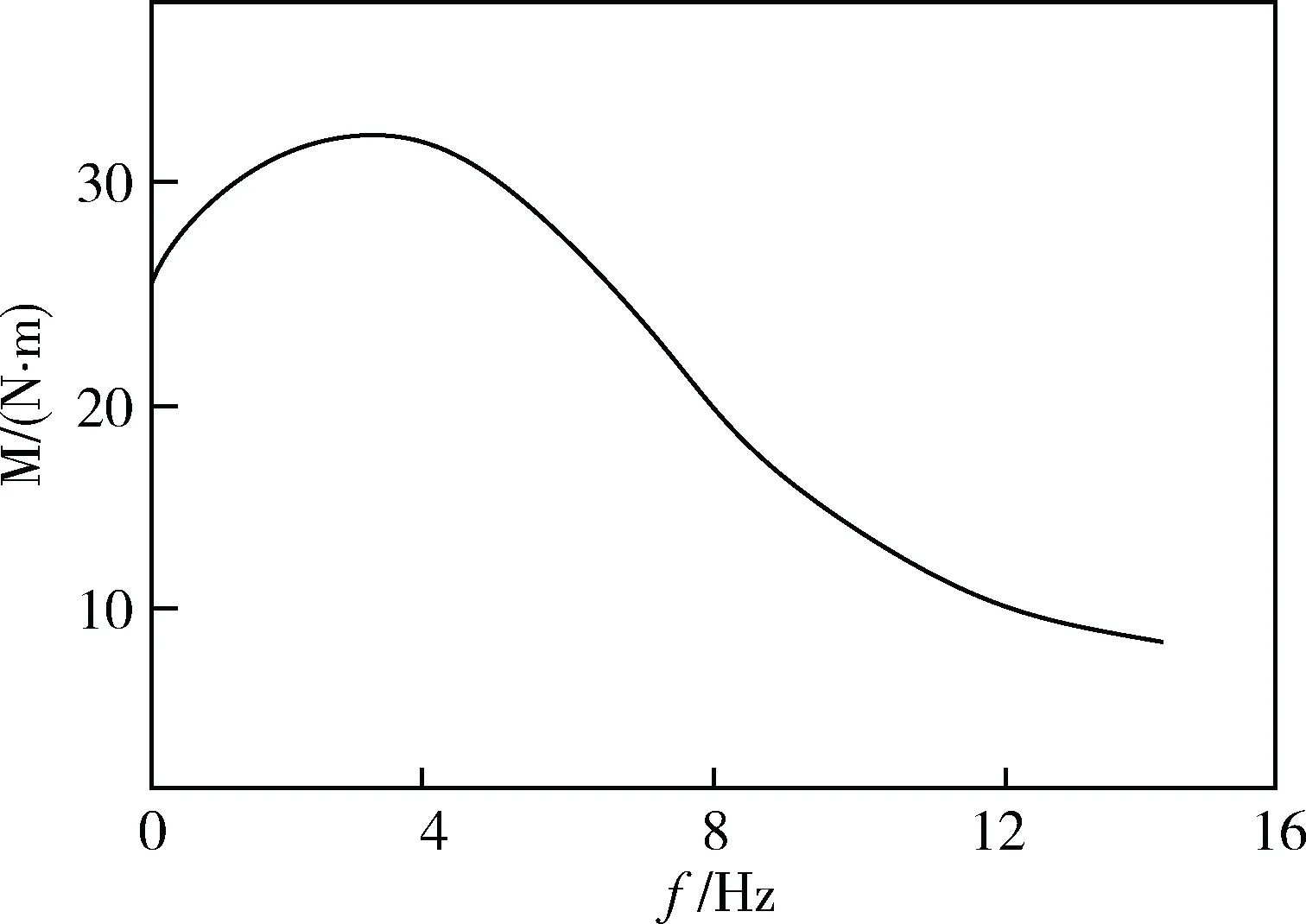
圖1 步進電機典型矩頻特性曲線

考慮到推力調節步進電機的慣性作用，在升速過程中，如果速率變化太大，電機響應將跟不上頻率的變化，出現失步。因此，每改變一次頻率，要求步進電機持續運行一定步數(稱階梯步長)，慢慢適應變化的頻率，使步進電機運行規律符合步頻特性曲線(圖2)，從而進入穩定的運行狀態。而減速過程中，如果速率變化太大，同樣存在電機響應跟不上頻率變化的現象，出現過沖，同樣影響控制精度。

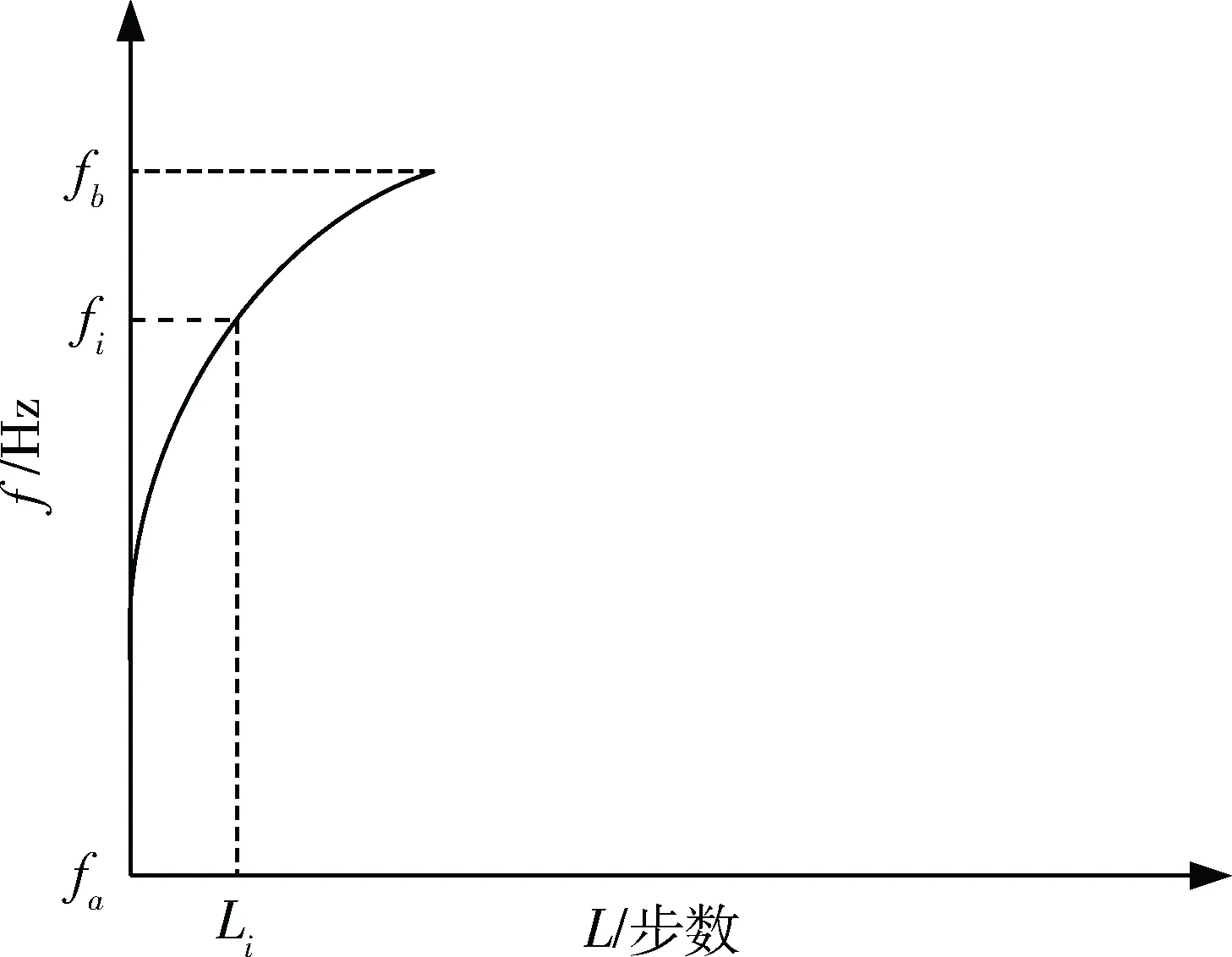
圖2 推力調節步進電機步頻特性曲線

指數曲線是從步進電機的矩頻特性和步頻特性出發，根據轉矩隨頻率的變化規律推導出來的。它符合步進電機加減速過程的運動規律，能充分利用步進電機的有效轉矩，快速響應性能好，升降時間短。指數型控制曲線如圖3所示。

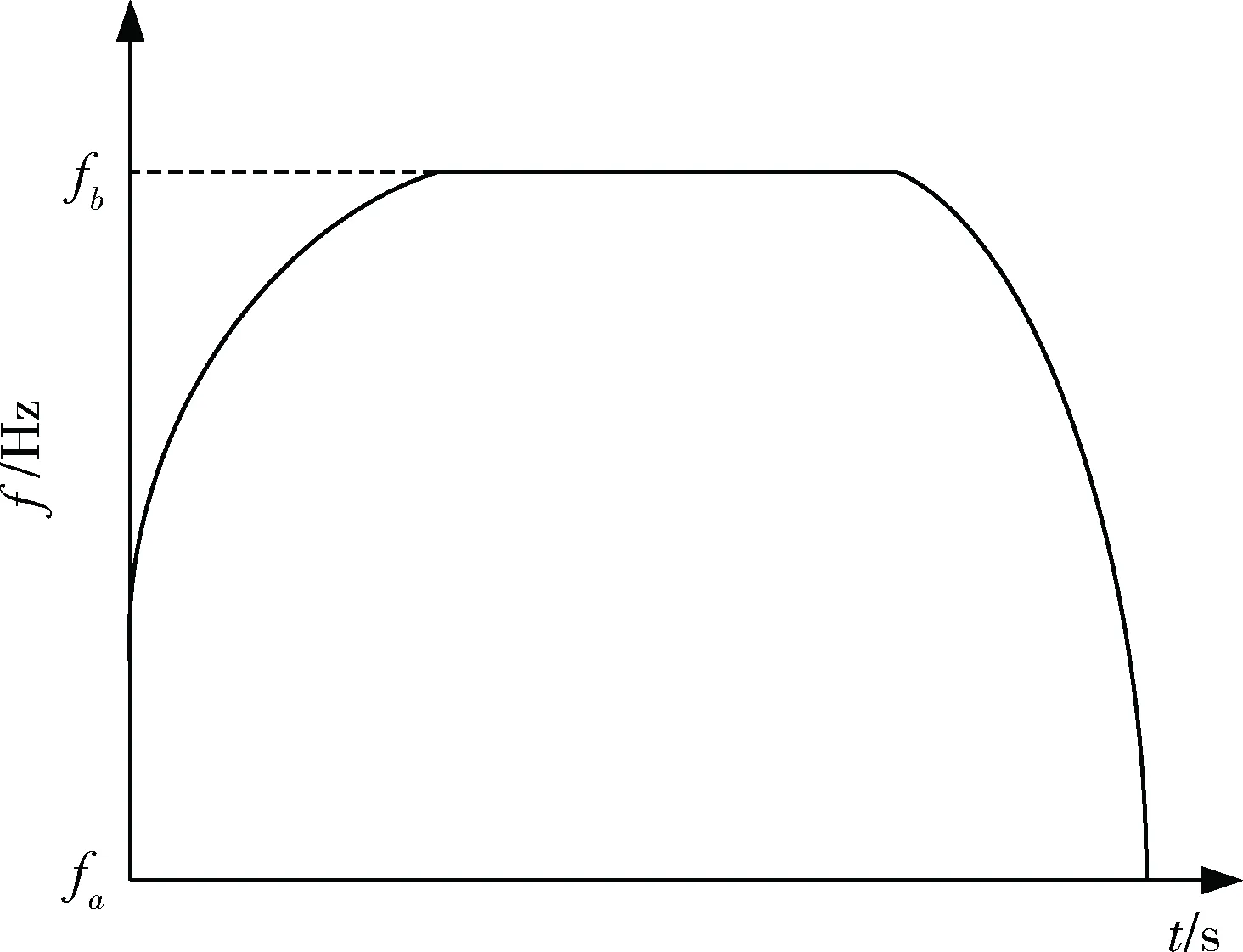
圖3 基于指數曲線的控制率

在實際運行過程中，當電機轉速升高時，由于反電動勢和繞組電感的作用，繞組電流將逐步減小，輸出轉矩有所下降，因此按指數規律升降速，加速度逐漸下降，接近電動機輸出轉矩隨轉速變化的規律，更符合實際應用。

2 指數型控制率的數學模型[4-6]

給一個電脈沖信號，步進電動機就轉動一個角度或前進一步，電機轉動角度和輸入脈沖成正比。設輸入脈沖頻率為f，步進電機的角速度為ω，則ω=Kf(f為驅動脈沖的頻率，K為步距角)，這是步進電動機輸入/輸出的比例關系。

假設Te為電磁轉矩，T為電機的輸出轉矩，TL為負載轉矩，Tf為電機的阻力矩。根據動力學原理，當步進電機克服阻力矩旋轉時，則有：

T=Te-Tf=TL

(1)

負載轉矩TL=Jω，J為電機的轉動慣量，阻力矩Tf=KTω，KT為轉矩常數，得到電機的運動方程：

(2)

假設電機從靜止開始加速，即t=0時，ω=0，則式(2)的解為：

(3)

其中，τ=J/KT。

由ω=Kf，則有f=ω/K，將式(3)帶入f=ω/K，整理得：

(4)

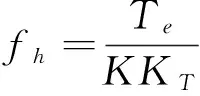
若運行頻率為fg，可以計算出升速時間

tr=τ[lnfh-ln(fh-fg)]

(5)

將加速段在時間上均勻地離散為N段，則相鄰2次速度變化的時間間隔為Δtr=tr/N，N即為階梯加速的分檔數。

由式(4) 可得每檔的頻率為：

fk=fh-fhe-kΔtr/τ,k=1,2,3,…,N

(6)

從而得到每一檔速度內運行步數Mk為

Mk=fkΔtr=fktr/N

(7)

由以上公式可以將速度曲線在時間上進行均勻離散化，但這種方法在應用中存在不便。首先為了擬合曲線需要細分很多加速檔，硬件實現上需要較大的存儲空間，軟件實現上也較為復雜；其次為了計算，需要用到精確的參數τ，由于參數τ取決于電機本身的屬性，又需要精準地確定電機的許多參數。因此，在實際應用中，如果嚴格按照式(4)去設計系統的速度控制曲線，離散化的過程會比較復雜。

對上述算法進行優化，簡化其在實際工程應用中的難度，將式(4)變為式(8)的表達式：

f(t)=fh-[(fh-f0)/k1]×e-k2t

(8)

其中，f0為初始運行頻率，取值范圍為0

為了便于計算，將式(8)進行離散化處理，得到：

(9)

其中，0

k2=-[ln(1-k1)]/Δt

(10)

根據上述分析，由式(9)和(10)可求得各級的頻率fn和運行時間Δtn，進一步可得各級的脈沖數：

Mn=fn×Δtn

(11)

3 應用舉例

下面介紹指數型速度控制率在運載火箭推力調節控制系統中的應用。該系統采用兩相混合式步進電機，電機組件工作頻率參數如下：

1)額定工作頻率：3200±200Hz；

2)起動頻率：800Hz。

整個指數曲線型推力調節步進電機的速度控制過程定義為升速段、勻速段和降速段。考慮到控制設備的內存空間和軟件實現復雜度，將升速段離散化過程分為16個頻點，從800Hz開始，到3100Hz結束，后面進入勻速段；勻速段步進電機的額定工作頻率為3200Hz；減速段從勻速段開始，為升速段的鏡像，按照與升速段頻點設置和脈沖分配逆序的規律，減速至800Hz，最后停止。

K1通常取值0.90～0.98之間，一般根據試驗選取，K1值越小，加速時間越長，加速過程越平穩，電機的輸出轉矩也就越大，電機在加速過程中越不容易產生失步，控制精度越高；反之，K1取值越大，加速時間越短，電機越容易發生失步，控制精度就越低，因此K1的取值需要結合加速時間和電機控制精度要求綜合考慮。綜合考慮到本例中系統對于電機調節過程的時間要求和精度要求，K1取0.955，既能得到較快的加速時間，電機的控制誤差也滿足系統精度要求。

根據式(9)～(11)，采用已知頻點求脈沖的方法，以發送10000個脈沖為例，求解方法如下：

1)設定升速段16個頻點分別為：

800，1000，1200，1400，1600，1800，2000，2200，2400，2500，2600，2700，2800，2900，3000，3100；

2)根據設定的頻率，采用式(9)和(10)，求得從啟動到每個頻率的累計運行時間Δtn，再根據式(11)求得各級脈沖數Mn分別為：8，19，25，32，41，53，68，88，117，73，88，108，137，183，267，471，升速段總脈沖數為1778，從而得到加速過程的控制率；

3)由于減速段為加速段的鏡像且順序相反，因此可以直接得到減速段的規律。減速段16個頻點：

3100，3000，2900，2800，2700，2600，2500，2400，2200，2000，1800，1600，1400，1200，1000，800；

每個頻點對應的脈沖數：

471，267，183，137，108，88，73，117，88，68，53，41，32，25，19，8；

減速段總脈沖數=升速段總脈沖數=1664；

4)勻速段頻率為電機額定工作頻率3200Hz，脈沖數根據加速和減速段的脈沖總數求得：勻速段脈沖數=總脈沖數-2*升速度段總脈沖數=10000-2*1778=6444，從而得到電機整個運動過程的控制率，見表1所示。

表1 指數型控制率舉例

將本例中的控制率進行擬合，得到如圖4所示的指數型曲線，可以看出，該控制率符合指數型理論控制率的曲線(圖3所示)。

圖4 控制率曲線

通過對采用本指數型速度控制曲線的推力調節電機各項功能性能指標進行測試，得出以下結論：

1)輸出轉矩

滿負載情況下可提供最大25N·m的控制力矩，滿足扭矩不大于15N·m的系統控制要求，且控制力矩存在較大余量；

2)控制誤差

通過對推力調節步進電機電位計阻值與理論阻值的偏差進行控制誤差分析，結果表明，該方法的控制誤差<1%，控制精度高于系統2%精度誤差的要求；

3)升降速時間

采用指數型控制率的步進電機升降速時間較短，取k1=0.955，在加速和減速過程各用時0.707s，10000個脈沖的情況下，整個運動過程耗時2.721s，通過調整k1的大小，可以調節加減速時間，最終獲得滿足力矩要求的加減速時間。

4 結論

基于指數曲線的速度控制率符合推力調節步進電機加減速過程的運動規律，能充分利用步進電機的有效轉矩，快速響應性能好，升降時間短，從而實現步進電機的平穩控制，避免啟動和停止過程的失步或過沖，滿足飛行控制對步進電機較高的實時性和精度要求。該運載火箭推力調節電機速度控制曲線經過多次發動機試車、動力系統試車以及飛行試驗驗證，運行穩定、精確。

[1] 崔潔，楊凱，肖雅靜. 步進電機加減速曲線的算法研究[J]. 電子工業專用設備，2013，18(5)：45-48. (Cui Jie, Yang Kai, Xiao Yajing. Algorithm Research in Acceleration and Deceleration of Stepper Motor[J]. Equipment for Electronic Products Manufacturing, 2013, 18(5): 45-48.)

[2] 曹東杰，韓峰，任云燕. 單片機控制步進電機按S形曲線升降頻設計[J]. 彈箭與制導學報，2006, 26(2): 157-159. (Cao Dongjie, Han Feng, Ren Yunyan. A Method to Accelerate or Decelerate the Speed of Step Motor Controlled by Singlechip Following S Curve [J]. Journal of Projectiles, Rockets, Missiles And Guidance, 2006, 26(2): 157-159.)

[3] 王玉琳，王強. 步進電機的速度調節方法[J]. 電機與控制應用，2006,33(1): 53-56. (Wang Yulin, Wang Qiang. Methods of Speed Regulation for Stepper Motor[J]. Electric Machines & Control Application, 2006, 33(1): 53-56.)

[4] 曾康玲，楊向宇，趙世偉. 步進電機指數型加速曲線優化與實現[J]. 微電機，2014,47(6)：36-40.( Zeng Kangling，Yang Xiangyu，Zhao Shiwei.Optimization of Exponential Acceleration Curve of Stepper Motor and Realization on PIC[J]. Micro Motors，2014, 47(6): 36-40.)

[5] 劉穎，王志剛，王紅. 步進電機升降頻的優化算法[J]. 微電機，2010, 43(8): 93-102.(Liu Ying, Wang Zhigang, Wang Hong.An Optimization Algorithm to Accelerate or Decelerate Speed of Step Motor [J]. Micro Motors, 2010, 43(8): 93-102.)

[6] 孫耀杰，王丹，等. 步進電動機升降速曲線的設計[J]. 微特電機，2006,34(5): 12-14. (Sun Yaojie, Wang Dan,et al. The Design of the Rise and Fall-speed Curve of Stepper Motor [J]. Small & Special Electrical Machines, 2006, 34(5): 12-14.)