邊坡風(fēng)險(xiǎn)評(píng)價(jià)動(dòng)態(tài)模型的構(gòu)建及其應(yīng)用*

趙 博， 張 翛， 元天宇

(1. 太原理工大學(xué) 建筑與土木工程學(xué)院， 太原 030024； 2. 山西省交通科學(xué)研究院 黃土地區(qū)公路建設(shè)與養(yǎng)護(hù)技術(shù)交通行業(yè)重點(diǎn)實(shí)驗(yàn)室， 太原 030006)

邊坡是一種復(fù)雜的地質(zhì)體，具有未知性、隨機(jī)性、模糊性和可變性等特點(diǎn)，據(jù)統(tǒng)計(jì)，每年所造成的直接經(jīng)濟(jì)損失多達(dá)50～60億元[1].風(fēng)險(xiǎn)分析通過查明系統(tǒng)中的各種不確定性因素，對(duì)其存在的危險(xiǎn)性做出分析與評(píng)價(jià)，對(duì)于確保邊坡工程的長(zhǎng)期穩(wěn)定和安全性具有重要的意義[2-3].目前，用于邊坡風(fēng)險(xiǎn)評(píng)價(jià)的方法主要有定性分析法、定量分析法和綜合分析法，例如德爾菲法、智爆法、蒙特卡羅法、概率統(tǒng)計(jì)法和敏感性分析法等[4-5].但是這些方法或多或少都存在缺陷，具有多屬性、不相容、定性與定量綜合評(píng)價(jià)的問題，如德爾菲法難以準(zhǔn)確量化，概率統(tǒng)計(jì)法中數(shù)據(jù)收集往往比較困難，且計(jì)算過程復(fù)雜[6].

因此，本文提出了基于馬爾科夫鏈法和物元可拓法來建立動(dòng)態(tài)的邊坡風(fēng)險(xiǎn)評(píng)價(jià)模型(MC-EE)，該綜合評(píng)價(jià)模型對(duì)多維數(shù)據(jù)進(jìn)行動(dòng)態(tài)分析，以尋求新的方法和途徑來認(rèn)識(shí)風(fēng)險(xiǎn)本質(zhì)和風(fēng)險(xiǎn)因子的性質(zhì)和相互聯(lián)系，追蹤和預(yù)測(cè)邊坡風(fēng)險(xiǎn)的變化規(guī)律.該模型的優(yōu)點(diǎn)是簡(jiǎn)單、容易掌握，對(duì)于多層次、多因素的復(fù)雜問題評(píng)判效果較好，很好地彌補(bǔ)了前述方法缺乏預(yù)測(cè)性和時(shí)效性差的缺陷，在減少人為主觀因素影響、提高評(píng)價(jià)結(jié)果的可靠性和時(shí)效性等方面，均起到了很好的作用.本文在詳細(xì)介紹該模型的原理、特點(diǎn)和算法后，將其應(yīng)用于實(shí)際邊坡工程的風(fēng)險(xiǎn)評(píng)價(jià)中，實(shí)例檢驗(yàn)其可行性及效果.

1 風(fēng)險(xiǎn)評(píng)價(jià)模型

1.1 物元可拓法

物元可拓理論(element extension theory，EE)[7-10]的基本思想是引入物元把處理研究對(duì)象間的矛盾問題變成處理物元之間的矛盾問題，將邊坡工程風(fēng)險(xiǎn)評(píng)價(jià)中的矛盾問題轉(zhuǎn)化為相容問題，從邊坡系統(tǒng)的組成部分和內(nèi)外關(guān)系去研究其安全性能，目前已廣泛應(yīng)用于各個(gè)領(lǐng)域，其具體步驟如下.

1) 確定邊坡風(fēng)險(xiǎn)狀態(tài)評(píng)價(jià)的物元.假定邊坡的名稱為N，對(duì)應(yīng)邊坡風(fēng)險(xiǎn)特征C的量值為V，有序三元組R=(N，C，V)稱為物元，其表達(dá)式為

R= (N，C，V)=

[對(duì)象特征c1特征值v1

特征c2特征值v2??

特征cn特征值vn]=[R1R2?Rn]

(1)

2) 建立評(píng)價(jià)模型，過程如下：

① 計(jì)算邊坡風(fēng)險(xiǎn)評(píng)價(jià)的單指標(biāo)關(guān)聯(lián)函數(shù).依次選擇某一待評(píng)物元，計(jì)算其關(guān)于各等級(jí)的關(guān)聯(lián)度，判定所屬等級(jí).把該待評(píng)對(duì)象N的第i個(gè)特征關(guān)于第j級(jí)別的關(guān)聯(lián)函數(shù)記為rj(vi(t))，i=1，2，…，n；j=1，2，…，m，具體的計(jì)算過程為

{rj(vi(t))=ρ(vi(t)，〈a0ij，b0ij〉)b0ij-a0ij(vi(t)∈〈a0ij，b0ij〉)
rj(vi(t))=ρ(vi(t)，〈a0ij，b0ij〉)ρ(vi(t)，〈api，bpi〉)-ρ(vi(t)，〈a0ij，b0ij〉) (vi(t)〈a0ij，b0ij〉)

(2)

式中，

(3)

其中，各變量的含義見文獻(xiàn)[7].

② 計(jì)算多指標(biāo)綜合關(guān)聯(lián)度.待評(píng)對(duì)象N關(guān)于級(jí)別j的關(guān)聯(lián)度計(jì)算公式為

(4)

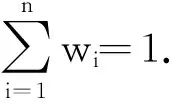
③ 確定邊坡風(fēng)險(xiǎn)級(jí)別的關(guān)聯(lián)度.采用熵權(quán)法[11-12]來確定各指標(biāo)的權(quán)系數(shù)，求得邊坡風(fēng)險(xiǎn)狀態(tài)針對(duì)各級(jí)別的關(guān)聯(lián)度Kjt，之后根據(jù)公式Kt(N)=max{Kjt(N)}即可判定待評(píng)邊坡N的安全級(jí)別屬于等級(jí)t，t為待評(píng)價(jià)邊坡所屬風(fēng)險(xiǎn)級(jí)別的特征值，其表達(dá)式為

(5)

式中，

(6)

詳細(xì)的物元可拓評(píng)價(jià)模型的計(jì)算流程如圖1所示.

1.2 馬爾科夫鏈法

馬爾科夫鏈法(Markov chain，MC)[13]的基本思路是對(duì)滿足馬爾科夫性的某事物，利用其狀態(tài)轉(zhuǎn)移概率來研究其動(dòng)態(tài)變化和未來發(fā)展趨勢(shì).該方法具有較高的準(zhǔn)確性和科學(xué)性，適用于隨機(jī)波動(dòng)性較大的時(shí)序，在現(xiàn)代預(yù)測(cè)方法中占有重要的地位，并逐步應(yīng)用于資源科學(xué)、地質(zhì)學(xué)、經(jīng)濟(jì)領(lǐng)域和自然災(zāi)害學(xué)等各個(gè)領(lǐng)域.

設(shè){Xk，k≥0}為馬爾科夫鏈，樣本數(shù)據(jù)X1，X2，…，Xk為馬爾科夫鏈的指標(biāo)值序列，選取距離預(yù)測(cè)時(shí)間最近的P個(gè)時(shí)步，依據(jù)距離的遠(yuǎn)近將轉(zhuǎn)移步數(shù)依次定為1，2，…，P.求出各轉(zhuǎn)移步數(shù)對(duì)應(yīng)的狀態(tài)轉(zhuǎn)移矩陣，從中選取起始狀態(tài)所對(duì)應(yīng)的行向量，將其組成新的概率矩陣G，對(duì)G的列向量求和，其和最大的轉(zhuǎn)移步數(shù)所對(duì)應(yīng)的狀態(tài)即為該時(shí)間序列的發(fā)展趨勢(shì).

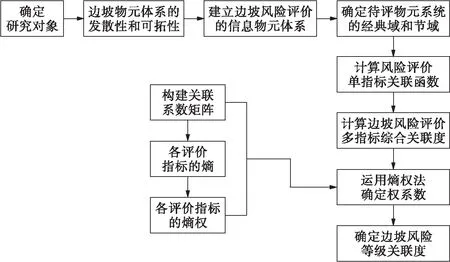
圖1 邊坡風(fēng)險(xiǎn)狀態(tài)的可拓評(píng)價(jià)流程圖Fig.1 Flow chart of extension evaluation for state of slope risk

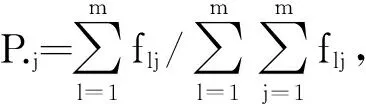
1.3 風(fēng)險(xiǎn)評(píng)價(jià)計(jì)算模型

由邊坡風(fēng)險(xiǎn)定義可知，對(duì)其評(píng)價(jià)是由危險(xiǎn)性評(píng)價(jià)和損失評(píng)價(jià)共同構(gòu)成，描述不確定因素與風(fēng)險(xiǎn)事件發(fā)生概率的關(guān)系，以及不確定因素與可能損失之間的關(guān)系.因此，本文提出了基于馬爾科夫鏈法和物元可拓法來建立邊坡的風(fēng)險(xiǎn)評(píng)價(jià)數(shù)學(xué)模型，融合危險(xiǎn)性評(píng)價(jià)和易損性評(píng)價(jià)二者所得到的失事概率和損失后果的計(jì)算結(jié)果用風(fēng)險(xiǎn)矩陣來分區(qū)表示，其優(yōu)點(diǎn)是模型簡(jiǎn)單、容易掌握，對(duì)于多層次、多因素的復(fù)雜問題評(píng)判效果較好.

依據(jù)最低合理可行原則(ALARP)，表1為風(fēng)險(xiǎn)的級(jí)別及基本對(duì)策.

表1 風(fēng)險(xiǎn)的分級(jí)及相應(yīng)對(duì)策Tab.1 Risk grades and corresponding countermeasures

表2為按照上述可拓評(píng)價(jià)步驟計(jì)算得到的風(fēng)險(xiǎn)矩陣列表，由失效可能性和造成損失后果的五個(gè)級(jí)別兩兩排列組合，形成了一個(gè)5×5的矩陣.

該方法將邊坡災(zāi)害、災(zāi)害特征和災(zāi)害特征值結(jié)合為一個(gè)整體，借助關(guān)聯(lián)函數(shù)計(jì)算來實(shí)現(xiàn)邊坡災(zāi)害的級(jí)別歸屬和安全性態(tài)的綜合描述判斷，實(shí)現(xiàn)了定性與定量綜合集成評(píng)價(jià)，利于揭示各因素之間的相互依賴關(guān)系和影響結(jié)果，從而更完整、深刻地反映了災(zāi)害的本質(zhì)，為邊坡風(fēng)險(xiǎn)分析提供直觀的查詢和參考依據(jù).

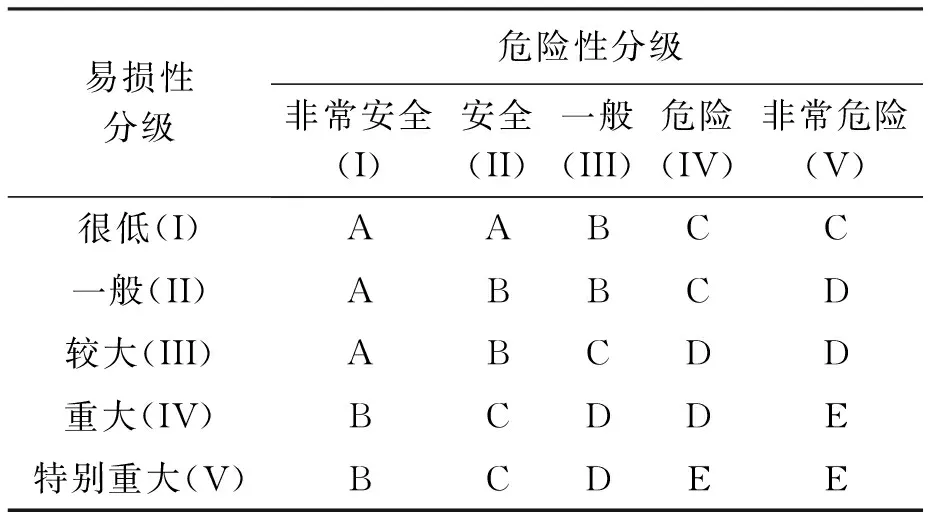
表2 風(fēng)險(xiǎn)評(píng)價(jià)矩陣列表Tab.2 Matrix of risk assessment

2 工程應(yīng)用

采用本文模型對(duì)某邊坡工程進(jìn)行動(dòng)態(tài)風(fēng)險(xiǎn)評(píng)價(jià)研究.該邊坡地處青藏高原向四川盆地過渡的斜坡地帶，地質(zhì)條件復(fù)雜，具有斷層、層間擠壓帶等不良地質(zhì)構(gòu)造，工程邊坡的安全穩(wěn)定性問題非常突出.因此，對(duì)其開展風(fēng)險(xiǎn)研究和分析工作并進(jìn)行合理地預(yù)測(cè)具有十分重要的意義.

2.1 確定風(fēng)險(xiǎn)等級(jí)

待評(píng)價(jià)邊坡的風(fēng)險(xiǎn)評(píng)價(jià)物元表達(dá)式為R= (N，C，V)=

計(jì)算待評(píng)邊坡N的第i個(gè)特征關(guān)于風(fēng)險(xiǎn)各等級(jí)的關(guān)聯(lián)度，其表達(dá)式為

同理可以求得其他關(guān)聯(lián)度，即

求出單指標(biāo)關(guān)聯(lián)度后，依據(jù)熵權(quán)法求得相應(yīng)權(quán)系數(shù)值，并計(jì)算多指標(biāo)關(guān)聯(lián)度.該邊坡關(guān)于各風(fēng)險(xiǎn)等級(jí)的關(guān)聯(lián)度計(jì)算結(jié)果如表3所示.

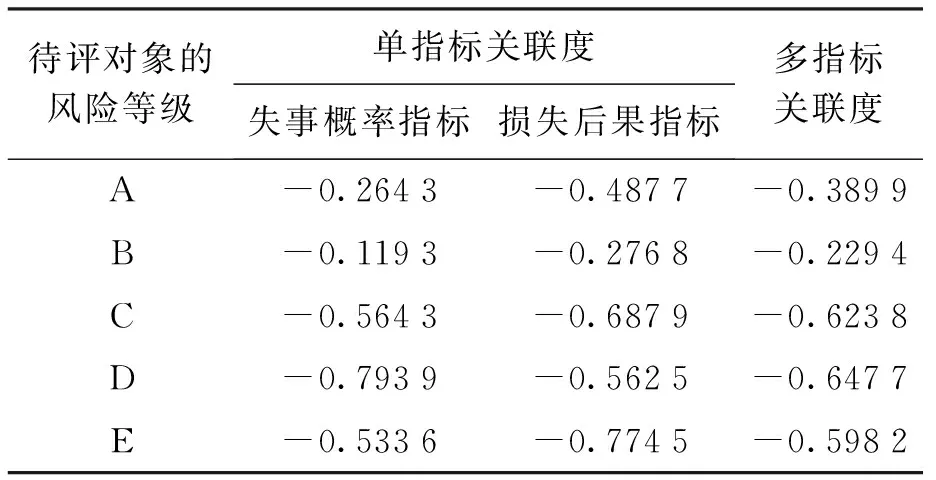
表3 邊坡物元可拓風(fēng)險(xiǎn)評(píng)價(jià)計(jì)算結(jié)果Tab.3 Calculated results of matter-element

最后綜合得出該邊坡的安全情況屬于B級(jí)，處于較低風(fēng)險(xiǎn)狀態(tài)，即使發(fā)生事故，所造成的后果相對(duì)輕微，無需專門考慮和關(guān)注.該邊坡工程的風(fēng)險(xiǎn)值處于可以接受的風(fēng)險(xiǎn)區(qū)域.

2.2 風(fēng)險(xiǎn)趨勢(shì)分析

對(duì)于邊坡工程來說，趨勢(shì)性分析是風(fēng)險(xiǎn)評(píng)價(jià)的重要環(huán)節(jié).由于監(jiān)測(cè)數(shù)據(jù)中蘊(yùn)含了大量豐富的變形信息，因此，本文根據(jù)已有的歷史監(jiān)測(cè)資料分析，采用馬爾科夫鏈法智能挖掘和統(tǒng)計(jì)其安全演化規(guī)律并預(yù)測(cè)風(fēng)險(xiǎn)發(fā)展趨勢(shì).將邊坡的監(jiān)測(cè)位移時(shí)序劃分為五個(gè)狀態(tài)S1、S2、S3、S4、S5，界限劃分結(jié)果如表4所示.

表4 狀態(tài)類型的劃分Tab.4 Division of state types mm

選取典型外觀測(cè)點(diǎn)TPL7進(jìn)行研究分析，該測(cè)點(diǎn)完整監(jiān)控了邊坡從開挖到現(xiàn)在的所有情況，包含安全等級(jí)的所有狀態(tài)，利用其完整信息來研究演化的規(guī)律和發(fā)展趨勢(shì).表5列出了該觀測(cè)點(diǎn)歷年的部分實(shí)測(cè)數(shù)據(jù).

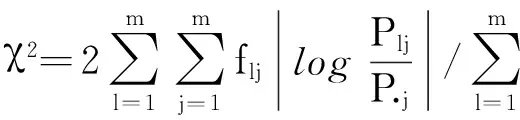
表5 部分年份的監(jiān)測(cè)位移量及其等級(jí)Tab.5 Monitoring displacement and grade in partial years

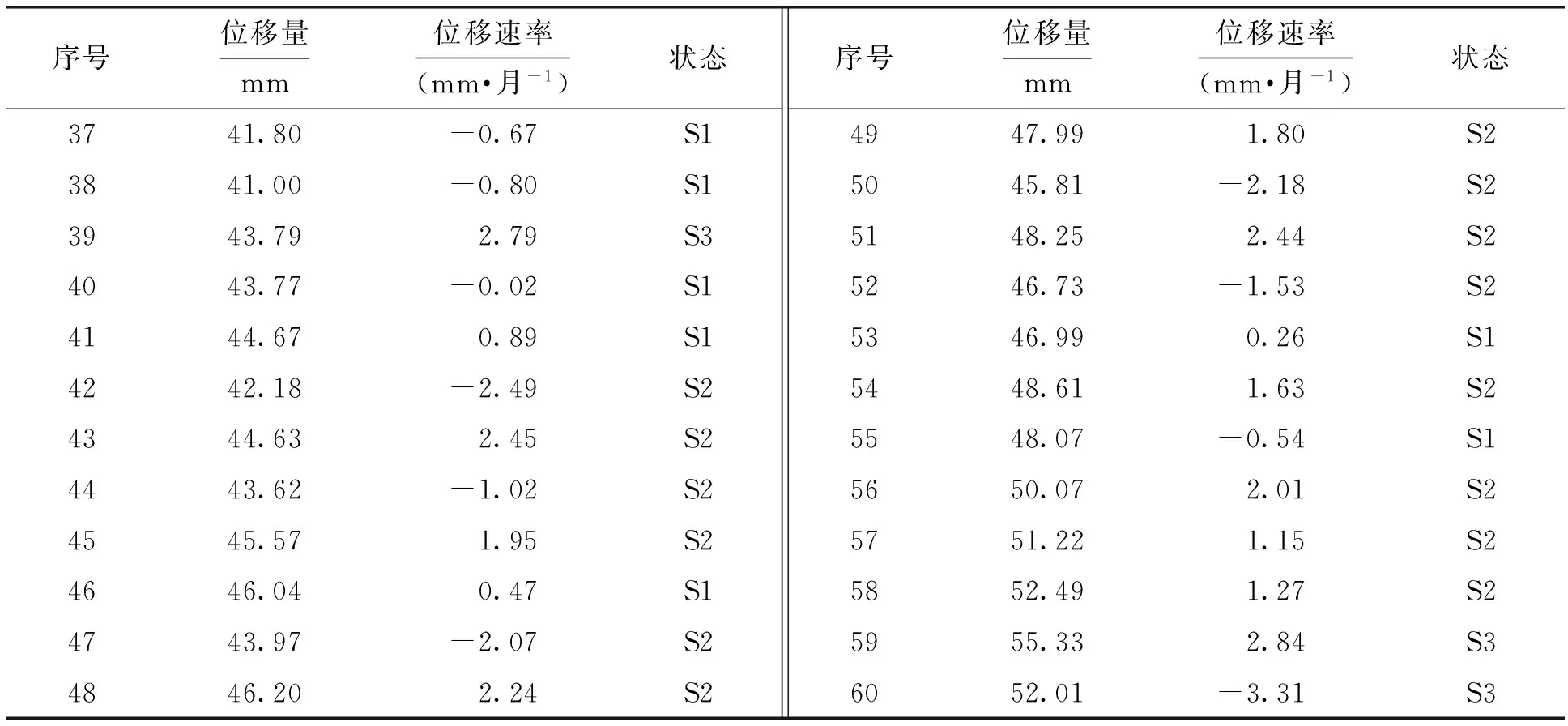
序號(hào)位移量mm位移速率(mm·月-1)狀態(tài)3741.80-0.67S13841.00-0.80S13943.792.79S34043.77-0.02S14144.670.89S14242.18-2.49S24344.632.45S24443.62-1.02S24545.571.95S24646.040.47S14743.97-2.07S24846.202.24S2序號(hào)位移量mm位移速率(mm·月-1)狀態(tài)4947.991.80S25045.81-2.18S25148.252.44S25246.73-1.53S25346.990.26S15448.611.63S25548.07-0.54S15650.072.01S25751.221.15S25852.491.27S25955.332.84S36052.01-3.31S3

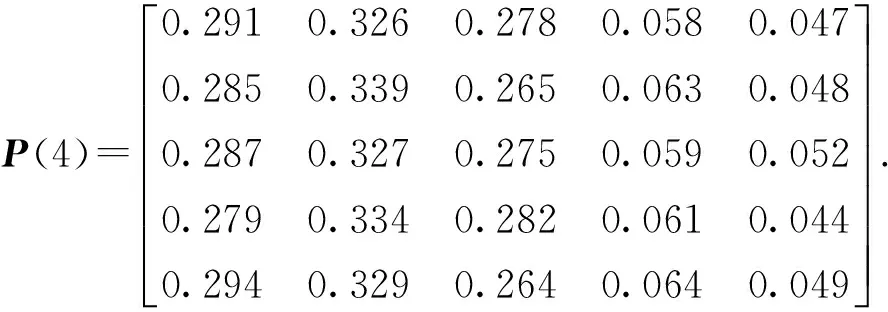
對(duì)該邊坡從1～6月份的安全性進(jìn)行預(yù)測(cè)，由于將時(shí)序劃分為5個(gè)狀態(tài)，所以選取離預(yù)測(cè)時(shí)間最近的時(shí)步編制預(yù)測(cè)表，轉(zhuǎn)移步數(shù)按時(shí)步的遠(yuǎn)近分別定為1、2、3、4.在轉(zhuǎn)移步數(shù)所對(duì)應(yīng)的轉(zhuǎn)移矩陣中，選取初始狀態(tài)的行向量組成新的轉(zhuǎn)移概率矩陣.對(duì)新的矩陣進(jìn)行列向量求和，其和最大的轉(zhuǎn)移步數(shù)所對(duì)應(yīng)的狀態(tài)即為系統(tǒng)的未來轉(zhuǎn)向狀態(tài)，相應(yīng)的結(jié)果如表6所示.

由表6可知，各時(shí)序狀態(tài)的預(yù)測(cè)概率疊加值分別為1.044、1.288、1.097、0.388、0.183，其中最大值為1.288，其預(yù)測(cè)所處的狀態(tài)為S2，即該月的位移量約在53.01～54.51 mm之間，而實(shí)測(cè)位移是53.83 mm，處于該范圍內(nèi)，說明預(yù)測(cè)結(jié)果與實(shí)際情況相吻合.

表6 1月份邊坡部位的風(fēng)險(xiǎn)狀態(tài)預(yù)測(cè)Tab.6 Risk state prediction of slope part in January

表7為2月份邊坡部位的風(fēng)險(xiǎn)狀態(tài)預(yù)測(cè).由時(shí)序58～61號(hào)的實(shí)測(cè)值預(yù)測(cè)第62個(gè)時(shí)序的位移值，即2月份的監(jiān)測(cè)值為53.46 mm，計(jì)算結(jié)果表明與實(shí)際相符合，進(jìn)一步論證了該方法的合理性和科學(xué)性.對(duì)3～8月份的風(fēng)險(xiǎn)狀態(tài)進(jìn)行動(dòng)態(tài)滾動(dòng)預(yù)測(cè)，結(jié)果如表8所示.

表7 2月份邊坡部位的風(fēng)險(xiǎn)狀態(tài)預(yù)測(cè)Tab.7 Risk state prediction of slope part in February

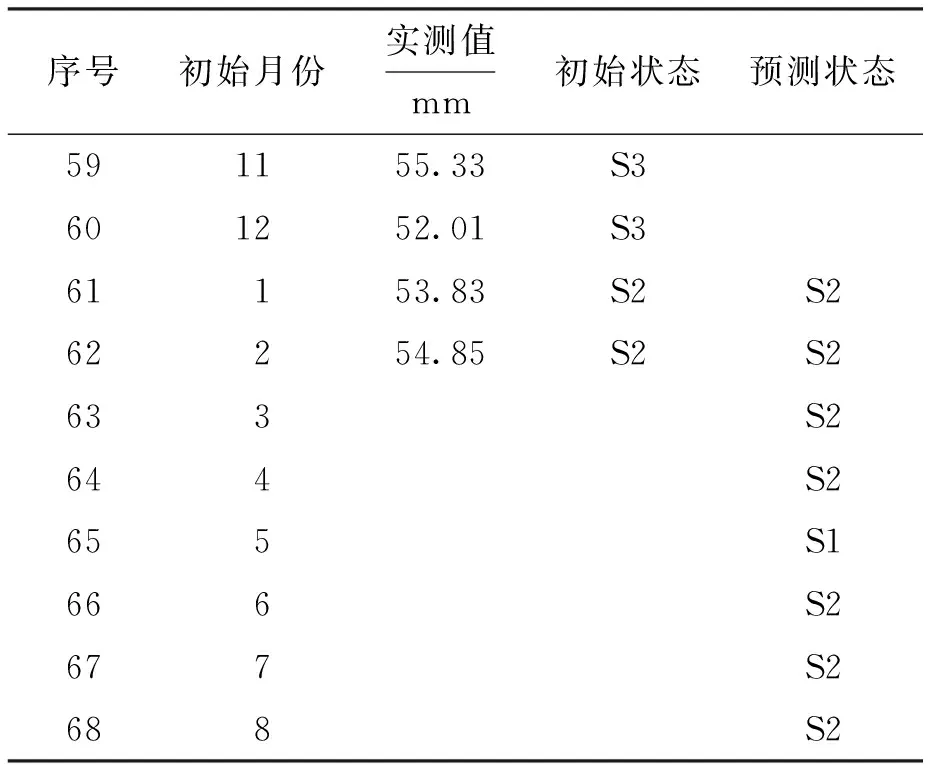
表8 位移時(shí)序的監(jiān)測(cè)值與預(yù)測(cè)值Tab.8 Monitored and predicted values ofdisplacement time sequence

從預(yù)測(cè)結(jié)果可以看出，目前邊坡的安全狀態(tài)為較低風(fēng)險(xiǎn)，未來的半年時(shí)間內(nèi)在“較低風(fēng)險(xiǎn)”和“低風(fēng)險(xiǎn)”之間波動(dòng)，沒有大的變化趨勢(shì)，比較穩(wěn)定，處于可以接受的風(fēng)險(xiǎn)狀態(tài)，能夠保證工程的正常運(yùn)行.

3 結(jié) 論

本文通過分析得出以下結(jié)論：

1) 將物元可拓法和馬爾科夫鏈法相結(jié)合，提出了一種動(dòng)態(tài)追蹤和預(yù)測(cè)邊坡風(fēng)險(xiǎn)變化規(guī)律的評(píng)價(jià)模型(MC-EE).將該模型應(yīng)用到邊坡工程的風(fēng)險(xiǎn)研究中，顯示了良好的預(yù)測(cè)效果，表明本文提出的MC-EE動(dòng)態(tài)風(fēng)險(xiǎn)評(píng)價(jià)模型具有較好的實(shí)際應(yīng)用價(jià)值.

2) 該模型從風(fēng)險(xiǎn)的概念出發(fā)，對(duì)數(shù)據(jù)動(dòng)態(tài)遞推分析，構(gòu)建的風(fēng)險(xiǎn)矩陣完成了從定性到定量的集成評(píng)價(jià)，將現(xiàn)場(chǎng)監(jiān)測(cè)數(shù)據(jù)納入風(fēng)險(xiǎn)評(píng)價(jià)體系來預(yù)測(cè)其變化趨勢(shì).本文研究方法在充分認(rèn)識(shí)風(fēng)險(xiǎn)的本質(zhì)和相互聯(lián)系后，動(dòng)態(tài)分析邊坡系統(tǒng)的整體風(fēng)險(xiǎn)，提高了風(fēng)險(xiǎn)評(píng)價(jià)結(jié)果的時(shí)效性和可靠性，預(yù)測(cè)結(jié)果更加準(zhǔn)確客觀.

[1] 鄭蓮婧.金沙江旭龍水電站左岸壩肩邊坡穩(wěn)定分析評(píng)價(jià) [D].長(zhǎng)春：吉林大學(xué)，2015.

(ZHENG Lian-jing.The analysis of left bank dam abutment slope stability of Xulong hydropower station of Jinsha river [D].Changchun：Jilin Univerxity，2015.)

[2] M?ller N，Hansson S O.Principles of engineering safety：risk and uncertainty reduction [J].Reliability Engineering & System Safety，2008，93(6)：798-805.

[3] 李典慶，肖特，曹子君，等.基于高效隨機(jī)有限元法的邊坡風(fēng)險(xiǎn)評(píng)估 [J].巖土力學(xué)，2016，37(7)：1994-2003.

(LI Dian-qing，XIAO Te，CAO Zi-jun，et al.Slope risk assessment using efficient random finite element method [J].Rock and Soil Mechanics，2016，37(7)：1994-2003.)

[5] Penna A，Lagomarsino S，Galasco A.A nonlinear macroelement model for the seismic analysis of masonry buildings [J].Earthquake Engineering and Structural Dynamics，2014，43(2)：159-179.

[6] Zhu H，Zhang L M.Evaluating suction profile in a vegetated slope considering uncertainty in transpiration [J].Computers and Geotechnics，2015，63(26)：112-120.

[7] 蔡文，楊春燕，林偉初.可拓工程方法 [M].北京：科學(xué)出版社，1997.

(CAI Wen，YANG Chun-yan，LIN Wei-chu.Extension engineering method [M].Beijing：Science Press，1997.)

[8] Saravanakumar R，Ali M S.Robust H∞control for uncertain Markovian jump systems with mixed delays [J].Chinese Physics B，2016，25(7)：108-113.

[9] 林登科，沈斐敏，廖素娟.基于可拓理論與區(qū)間賦權(quán)的煤礦水害安全評(píng)價(jià) [J].安全與環(huán)境工程，2015，22(2)：124-128.

(LIN Deng-ke，SHEN Fei-min，LIAO Su-juan.Research on safety evaluation of coal mine water hazard based on extension theory and interval empowerment [J].Safety and Environmental Engineering，2015，22(2)：124-128.)

[10]趙博，徐衛(wèi)亞，張冬梅，等.基于安全監(jiān)測(cè)信息的巖石高邊坡穩(wěn)定性評(píng)價(jià) [J].沈陽工業(yè)大學(xué)學(xué)報(bào)，2014，36(1)：100-105.

(ZHAO Bo，XU Wei-ya，ZHANG Dong-mei，et al.Stability evaluation of high rock slope based on safety monitoring information [J].Journal of Shenyang University of Technology，2014，36(1)：100-105.)

[11]周惠成，張改紅，王國利.基于熵權(quán)的水庫防洪調(diào)度多目標(biāo)決策方法及應(yīng)用 [J].水利學(xué)報(bào)，2007，38(1)：100-106.

(ZHOU Hui-cheng，ZHANG Gai-hong，WANG Guo-li.Multi-objective decision making approach based on entropy weights for reservoir flood control operation [J].Journal of Hydraulic Engineering，2007，38(1)：100-106.)

(ZHOU Jia-kuan，ZHENG Bo-ning，ZHAO Hong-ze.Slope stability evaluation based on the extension theory combined with entropy weight [J].Opencast Mi-ning Technology，2016，31(7)：26-30.)

[13]Desharnais J，Edalat A，Panangaden P.Bisimulation for labelled Markov processes [J].Information & Computation，2015，179(2)：149-158.